ARIMA모델로 시계열 예측(차분, AR(p),MA(q)차수 구하기)

AR(p) 모델

• 현재 차수(Yt)의 결과는 이전차수(Yt-1)의 결과에 영향을 받는모델이다.
• 즉, 자신의 데이터가 이후 자신의 미래 관측값에 영향을 준다는 것을 기반으로 나온 모델이다.
  
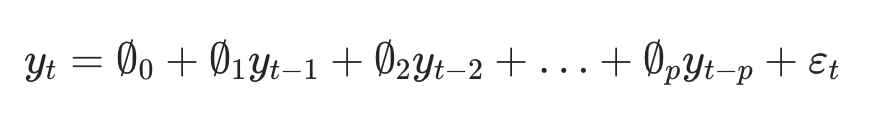
• 외부 충격이 길게 반영되는 Long Memory 모델이다.

MA(q) 모델

• 이번 차수(Yt)의 결과는 이전차수(Yt-1)의 결과와 상관이 없다.
• 예측 오차를 이용하여 미래를 예측하는 모델이다.
  

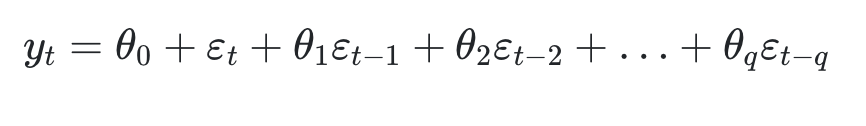
ARIMA(p,k,q) 모델

• ARMA 모델이 과거의 데이터들을 사용한 모델인것에 반해 ARIMA 모델은 과거의 데이터가 지니고 있던 추세까지 반영하고, 파라미터 K 즉, 차분횟수를 포함하여 정상성을 만족하게 하는 모델이다.
• 만약 ARIMA(2,1,2)모델일 경우 AR(2), MA(2), 차분(k)1회 인 것이다.

ARIMA모델링 하기

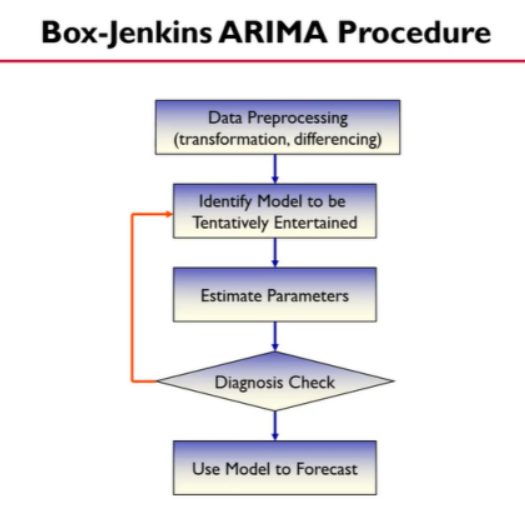
Box_jenkins의 방법을 활용하여 모델링을 해보겠습니다.

- 첫 번째,데이터를 전처리한다.(non stationary한 데이터 일경우,차분과 같은 과정을 통해 stationary하게 만들어준다.)
- 두 번째, 시범적으로 할 베이스 모델을 만든다. -> 도표를 통해 베이스모델을 만들기때문에 주관적이므로 시범적인 선정 과정이라고 한다.
- 세 번째, 파라미터 추정
- 네 번째, 추정한 파라미터가 모델로서 적합한지 테스트 하는과정이다. 이 과정에서 모델이 적합하지 않다면 두 번째 단계로 돌아간다.
- 다섯 번째, 최종모델을 통한 예측 실시

1. 정상성(안정성) 검증

정상성은 먼저 Augemented Dickey Fuller Test 를 통해 확인해 보자, 데이터는 환율 데이터를 사용한다(이전 시계열데이터 포스팅에서 사용한 데이터와 동일)

먼저 데이터를 시각화 하면 아래와 같다.

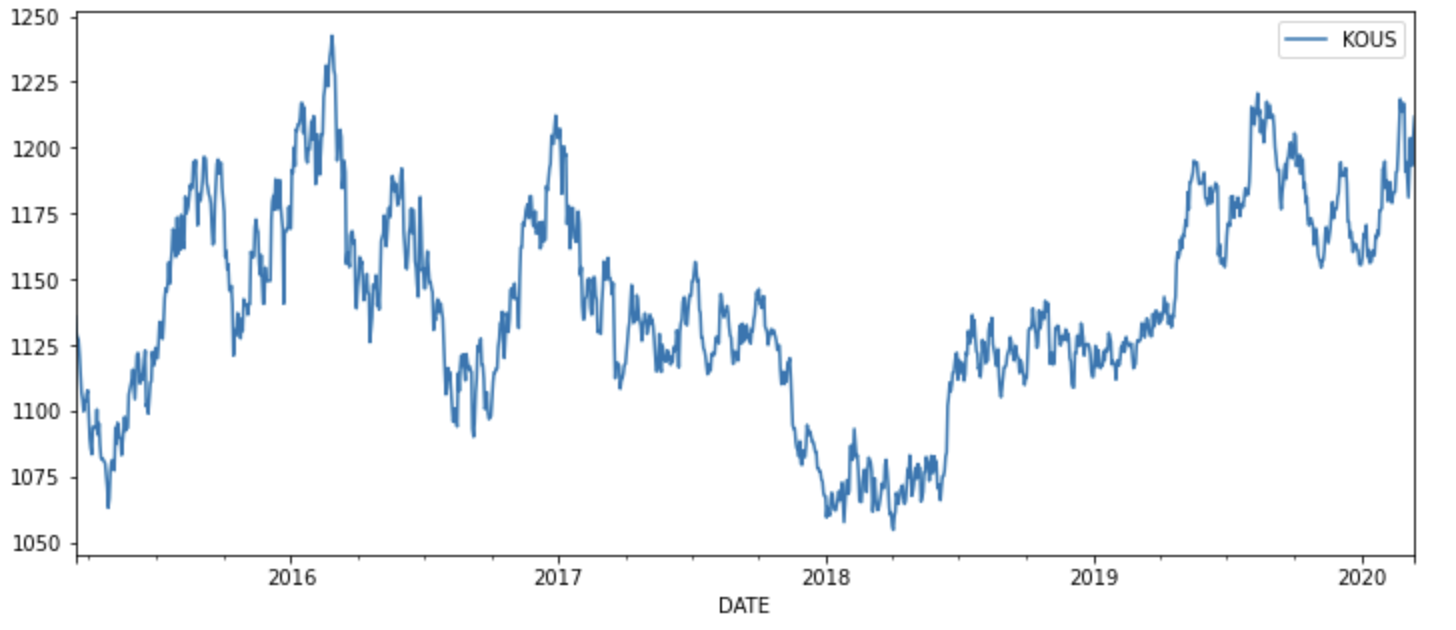
1-1. Augemented Dickey Fuller Test를 통한 검증

adfuller(df['KOUS'] # KOUS 는 환율 데이터가 들어있는 컬럼 명칭
>>>
(-1.834289925068011,
 0.36357542996557135,
 2,
 257,
 {'1%': -3.4560535712549925,
  '10%': -2.5727985212493754,
  '5%': -2.8728527662442334},
 1453.3457437081727)

시각적으로 봤을때도 정상성이 만족하지 않은것을 대략적으로 알 수 있었지만, Augemented Dickey Fuller Test를 통해 p-value>0.05를 훨씬 넘는 0.36이 나오는것을 보아 정상성을 만족하지 않는다고 생각해 볼 수 있다.

1-2. 자기상관함수(Auto Correlation Function)도표를 통한 검증

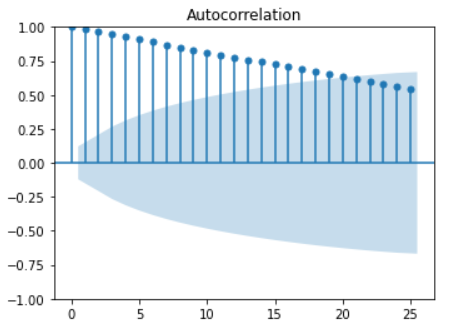
ACF도표를 통해 확인해본 결과 시차에 따라 천천히 내려가며 t(시차)가 20일때까지 상관관계를 가지는 전형적인 non stationary 한 데이터임을 알 수 있다.

2. 데이터 분리하기

train_df, test_df = train_test_split(df, test_size = 0.2, shuffle = False)

모델링을 위한 파라미터를 찾거나 분석을 할때는 데이터를 분리해주는것도 중요하다.

3. Identify Model to be Tentatively Entertained(시범모델 찾기)

3-1. 차분 파라미터 d 구하기

먼저 ARIMA(p, d, q)모델에서 d값 즉, 차분을 몇회해야하는지 먼저 찾아보자.

# Augemented Dickey Fuller Test
adfuller(df['KOUS'].diff().dropna())
>>>
(-10.572632524492832,
 7.239046680336767e-19,
 1,
 257,
 {'1%': -3.4560535712549925,
  '10%': -2.5727985212493754,
  '5%': -2.8728527662442334},
 1446.168602565303)

1회 차분을 한 결과 바로 0에 가까워지는 것을 확인할 수 있다. 그렇다면 차분 전후 데이터의 ACF, PACF도표를 비교해보자

# 차분 데이터 저장
diff_train_df = train_df.KOUS.diff().dropna()
# 시각화
plt.figure(figsize= (12,8))
plt.subplot(311)
plt.plot(train_df)
plt.legend('RawData')
plt.subplot(312)
plt.plot(diff_train_df, 'orange')
plt.legend('DifferencedData')
plt.show()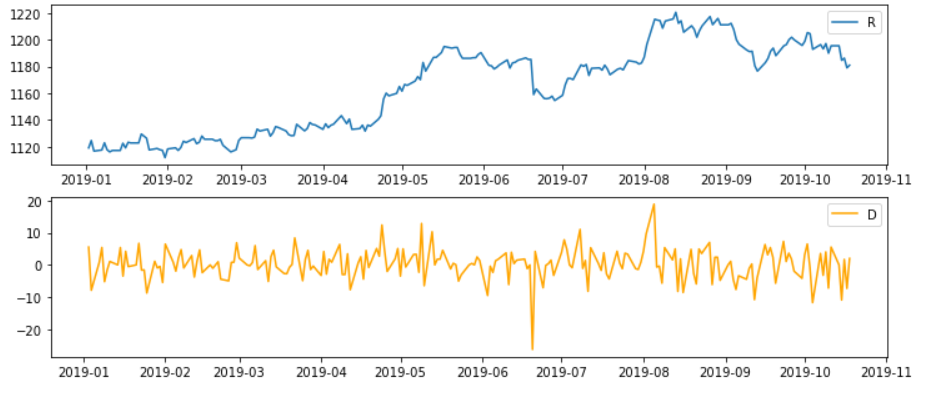

확실히 평균이 0이고 분산이 비슷해진 모습을 보이고 있다.

3-2. Graphical method를 통한 AR, MA차수 구하기

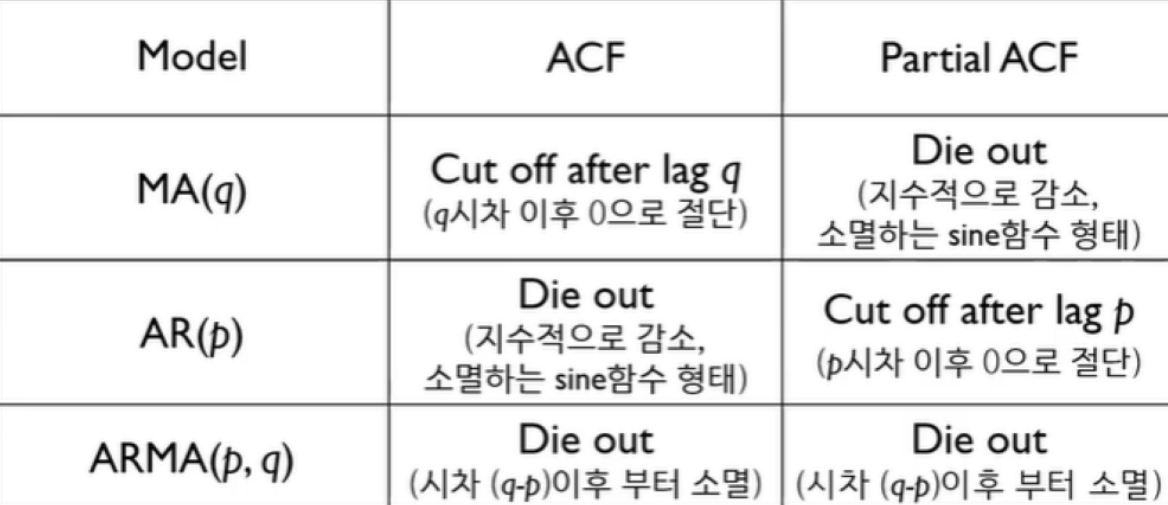
위의 표를 보면 임시모델을 만드는 이유가 나오는데, 어떤 모델을 쓸지 베이스 모델을 정하는 참고자료이며, 내용을 보면 ACF, PACF도표를 참고하기 때문에 주관이 포함되어 있어 임시 모델이라고 부르며, 추후 임시모델을 기준으로 fit하는 방식으로 진행된다.

fig, ax = plt.subplots(2,1, figsize=(8,8))
plot_acf(df['KOUS'], ax[0])
plot_pacf(df['KOUS'], ax[1])
plt.show()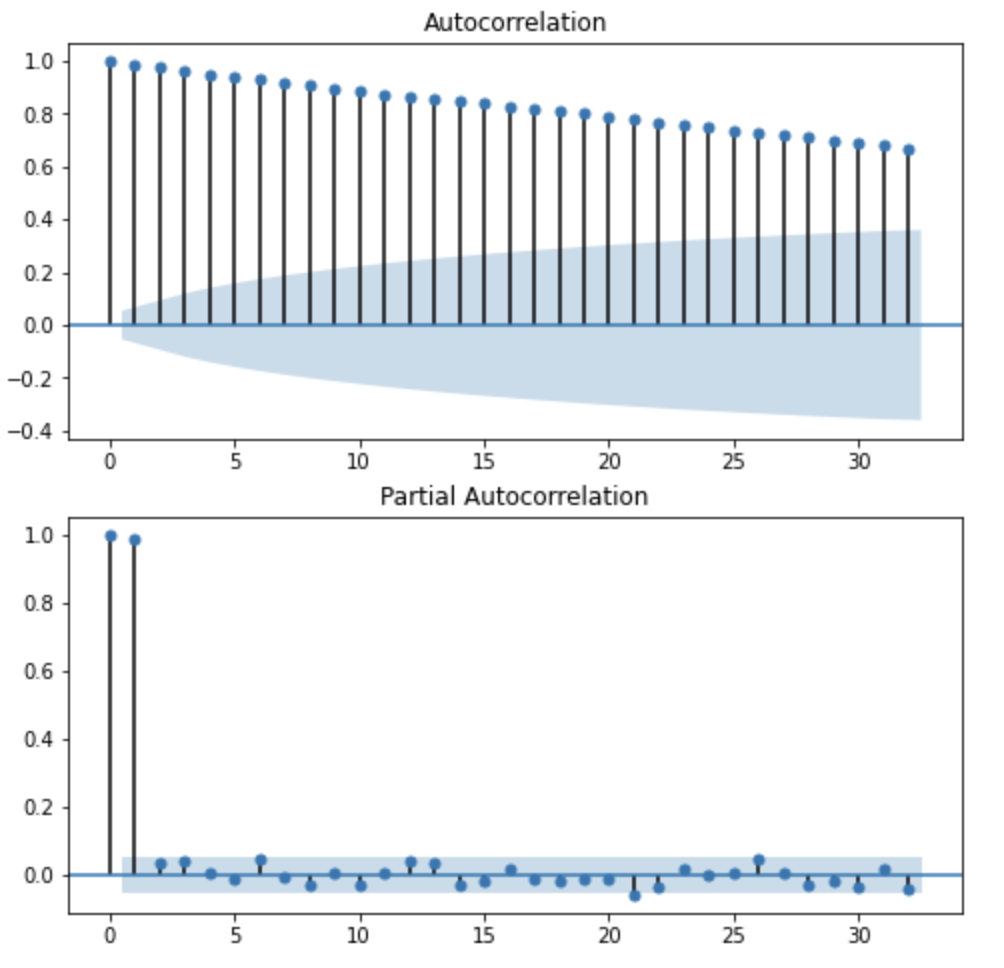

우선 위의 그래프를 보았을때 PACF도표는 1차시 이후 급격하게 감소하는 모습을 보이고 있으며 ACF는 지수적으로 천천히 감소하는 모습이다. AR(1)모델이 어울려 보인다.

ACF도표로는 MA의 차수를 알수 없기때문에 1회차분을 통해 MA의 차수를 확인해보자

fig, ax = plt.subplots(2,1, figsize=(8,8))
plot_acf(df['KOUS'].diff().dropna(), ax[0])
plot_pacf(df['KOUS'].diff().dropna(), ax[1])
plt.show()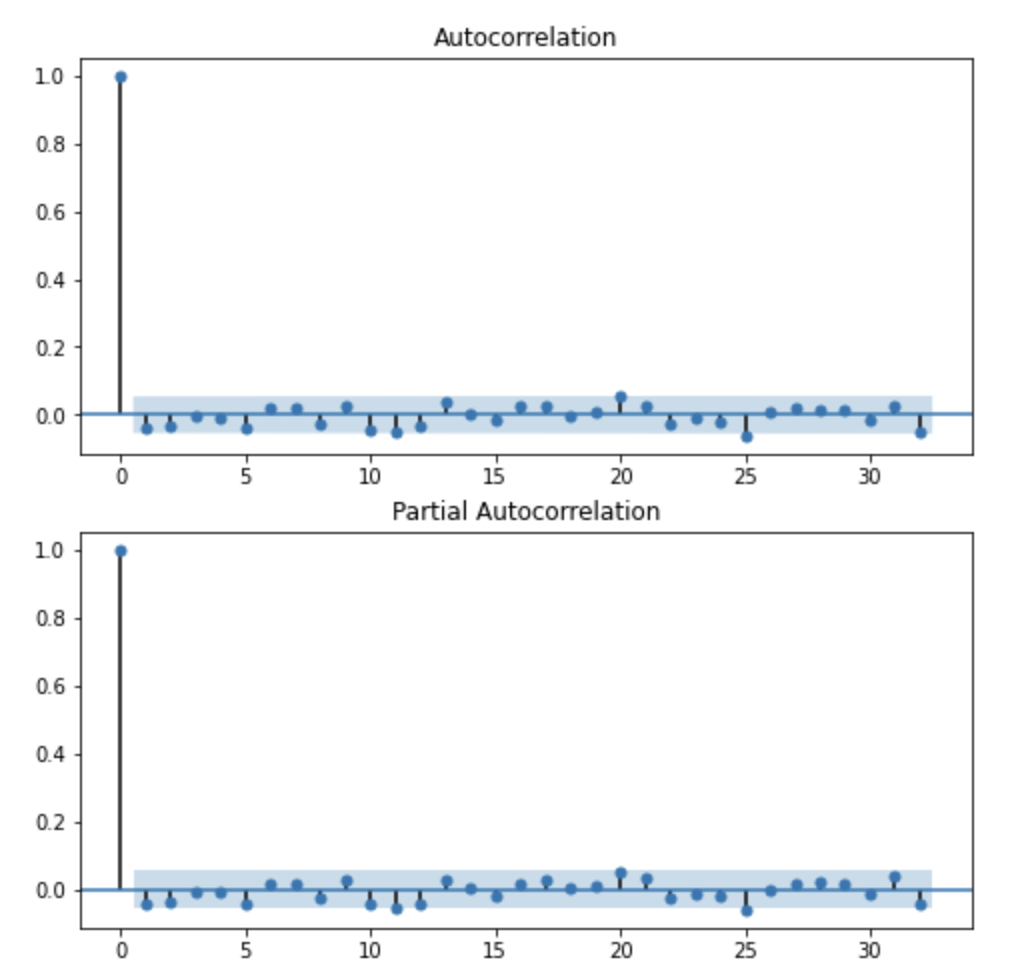

차분후 ACF plot을 찍어본 결과 딱히 급격히 감소되거나 지수적으로 감소하는 모습을 볼 수 없기때문에 일단 MA는 0으로 하고 AR(1)모델만 적용시켜보자

이렇게 주관적인 해석이 들어가기 때문에 임시 베이스모델이라고 보면된다.
지금 정한 모델을 고정해서 최종사용하는것이 절대 아니다.

3-3. 임시모델 테스트

model =ARIMA(train_df, order = (1,1,0), freq = 'B')
model_fit = model.fit()
model_fit.summary()

< 파라미터 설명 >

- freq : 날짜주기(ex, 월 ~ 금 : 'B' (business date), 'D'(Daily),  'W' (Weekly)
- trend : 상수항 포함여부-> 'nc' (no constant), 'c'(constant) ->'c'를 넣었을때 constant의 p-value값이 0.05이상이면 'nc'를 사용한다.(p값이 0.05보다 크면 귀무가설이 기각 -> 상수항 변수는 유효하지 않다.)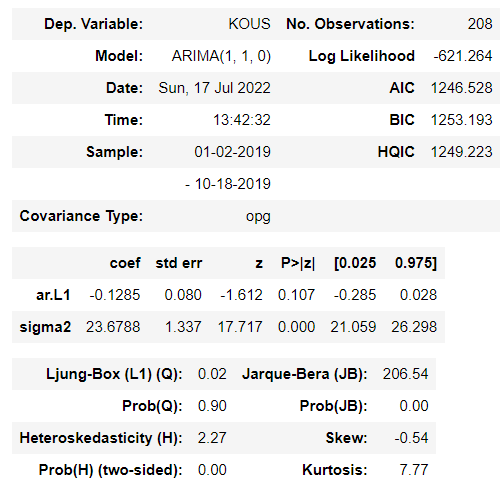

summary를 찍어보면 다음과 같은 표가 나온다. 이때 우리는 해당 모델이 적합한지 확인해봐야 하는데 이때 AIC 점수를 보고 판단을 할 수 있다.

하지만, 임시 파라미터를 통한 결과 하나만을 가지고 좋은 AIC 점수값인지 알 수 없기때문에 여러가지 파라미터를 넣어보면서 비교해볼 수 있다.

3-4. 비교해볼 파라미터 적용해보기

# Parameter search

p = range(0,3)
d = range(0,3)
q = range(0,3)
pdq = list(itertools.product(p, d,q))

aic = []
for i in pdq:
    model = ARIMA(train_df, order = (i))
    model_fit = model.fit()
    print(f'ARIMA: {i} >> AIC : {round(model_fit.aic,2)}')
    aic.append(round(model_fit.aic,2))
    
# Search optimal parameters
optimal = [(pdq[i],j) for i, j in enumerate(aic) if j == min(aic)]
optimal

>>>
[((2, 1, 0), 1246.37)]

먼저 코드를 설명하면 p,d,q 파라미터에 각각 0, 1, 2 인경우를 for문으로 돌려보면서 AIC값이 가장 적은 값이 나오는 파라미터를 찾는 코드이다.
(AIC점수가 가장 적은 파라미터가 가장 적합하다고 할 수 있다.)

우리는 ARIMA(2,1,0)파라미터가 AIC 점수가 1246.37 로 좋은 점수라는 것을(가장 낮은점수) 알게되었다. 이를 적용해서 다시 summary를 찍어보자

model =ARIMA(train_df, order = optimal[0][0], freq = 'B')
model_fit = model.fit()
model_fit.summary()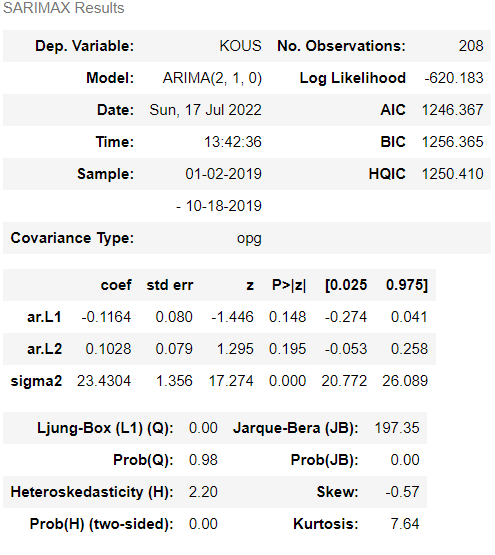

실제로 AIC점수가 for문을 돌린 코드와 같이 점수가 나오는것을 확인할 수 있다.

4. 모델 적합성 검증

우리는 여러 경우의 수 중에서 ARIMA(2,1,0)이 가장 적절한 모델이라는 것을 확인했고 마지막으로 사용하기전 최종적으로 모델 적합성을 검증해 봐야한다. 만약 이번 단계에서 적합하지 않다고 판단되면 다시 파라미터를 찾아야한다.

4-1. 잔차(Residual)의 ACF(Auto Correlation Function)도표를 통한 검증

첫 번째 방법으로 만든 모델의 잔차들을 ACF도표를 그려봄으로서 확인 해 볼수있다.

plot_acf(model_fit.resid)
plt.show()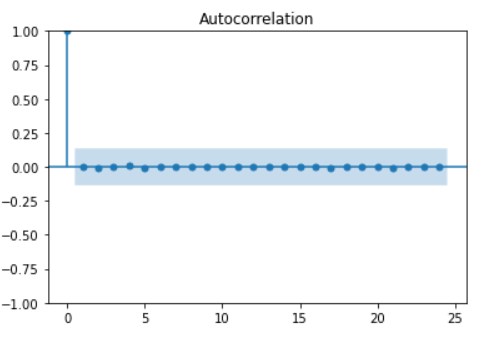

일단 ACF도표상으로 매우 stationary하다고 생각할 수 있다.

4-2. Argumentd dickey fuller test

두번째 방법으로 잔차의 Argumentd dickey fuller test를 통해서 p-value를 추정해보고 검증해볼 수 있다.

adfuller(model_fit.resid)
>>>
(-229.88752781133704,
 0.0,
 0,
 207,
 {'1%': -3.4623415245233145,
  '5%': -2.875606128263243,
  '10%': -2.574267439846904},
 1158.1846984038439)

두번째 원소를 보면 p-value가 0.0으로 귀무가설(안정적이지 않다)을 기각하여 대립가설(안정적이다, stationary하다)을 채택할 수 있다.

5. 예측하기

model = ARIMA(train_df, order = (2,1,0), freq = 'B')
model_fit = model.fit()

우리가 최종으로 정한 ARIMA모델을 만들어준다.

result = model_fit.get_forecast(steps = len(test_df.index), alpha = 0.05).summary_frame()
result

예측을 하는 코드를 작성한 것이다. steps = len(test_df.index) 코드는 몇개를 예측할것이냐는 내용을 작성하는것인데 테스트 데이터의 인덱스 갯수만큼 예측값을 뽑기를 원해서 위와 같이 작성을 하였고, 코드를 실행하면 아래와 같이 나온다.

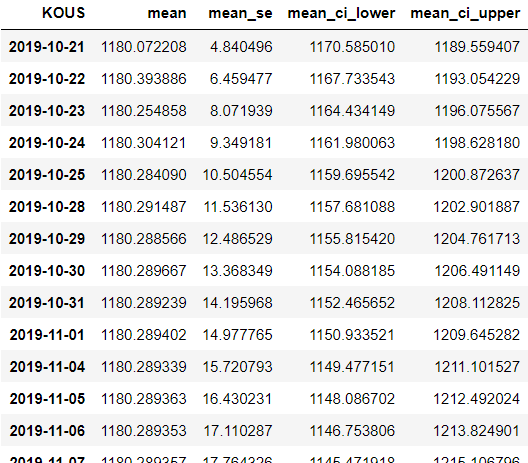
12월31일 까지 있지만 길어서 끊어서 가져왔다.

• mean 컬럼 : 예측값의 평균
• mean_se : 표준오차
• mean_ci_lower : 신뢰구간 min값
• mean_ci_upper : 신뢰구간 max값

다음은 시각화를 해주기 위해 위에있는 컬럼을 각각의 데이터로 만들어준다.

fc = tuple(result['mean'].values) # 예측값
se = tuple(result['mean_se'].values) # 표준오차
lower_coef = tuple(result['mean_ci_lower'].values) # 신뢰구간 최소
upper_coef = tuple(result['mean_ci_upper'].values) # 신뢰구간 최대

# 예측값 인덱스 넣기
fc_data = pd.Series(fc, index = test_df.index)

# 신뢰구간 인덱스 넣기
lower_data = pd.Series(lower_coef, index = test_df.index)
upper_data = pd.Series(upper_coef, index = test_df.index )

그리고 시각화를 하면 아래와 같은 결과가 나오게된다.

#시각화 
plt.figure(figsize =(15, 6))
plt.plot(train_df, label = 'training')
plt.plot(test_df, label = 'actual')
plt.plot(fc_data, label = 'forecast')
plt.fill_between(test_df.index, lower_data, upper_data, color = 'black', alpha = 0.1)
plt.legend(loc = 'upper left')
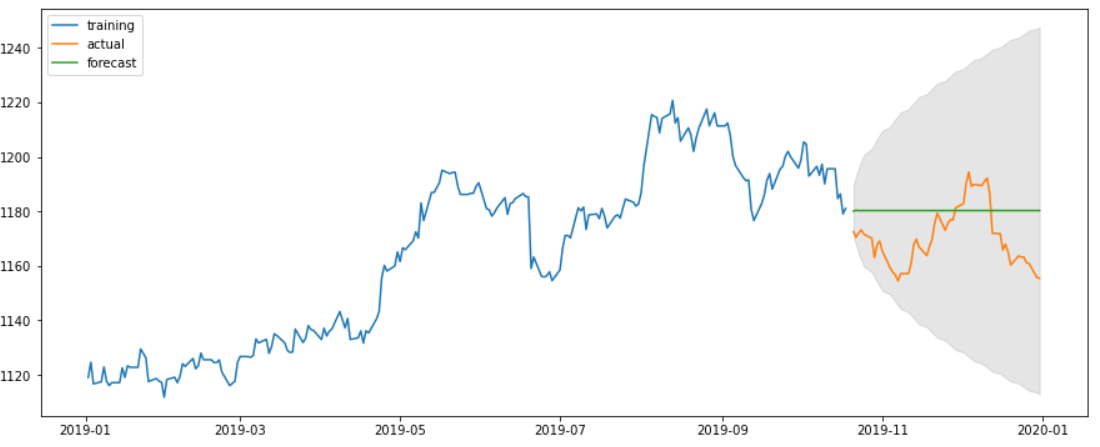
plt.show()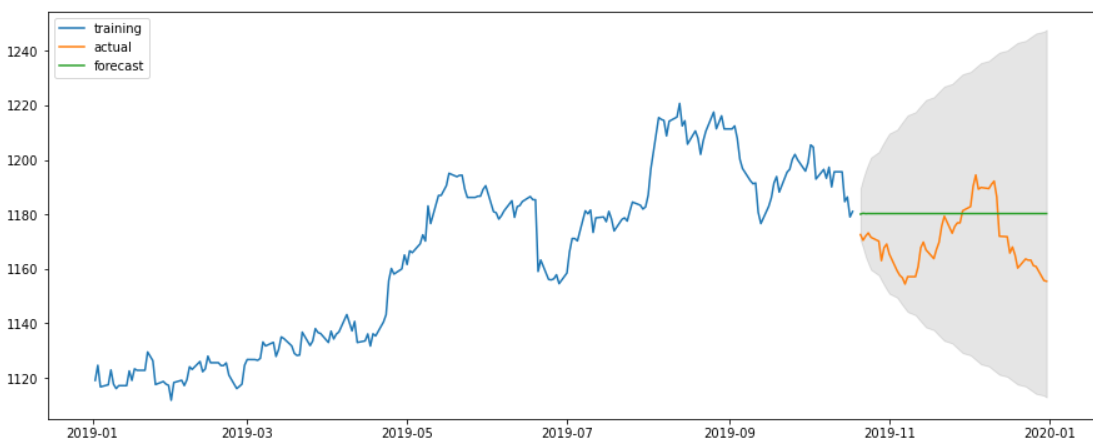

결과를 보면 의아할 것이다. 이렇게 열심히 해놓고 결과는 처참하다...

하지만, 우리의 데이터는 환율에 대한 데이터이다. 환율은 한가지 요소 즉, 단변량 시계열 분석으로 예측할 수 없다... 여러가지 요소들이 합쳐져있고, 무엇보다 예측하기 힘든 외부요소들이 너무많다... 따라서 결과보다는 ARIMA분석의 과정에 초점을 두면 될것같다.