회귀란??

회귀는 여러 개의 독립 변수와 한 개의 종속 변수 간의 상관관계를 모델링 하는 기법을 말한다.

회귀의 종류

<이미지 출처 : http://mcheleplant.blogspot.com/2019/01/lab-2.html>

회귀모델은 위의 사진과 같이 구분을 할 수 있다. 독립변수가 1개이면 단순회귀(Simple Regression), 독립변수가 2개이상 이면 다중회귀(Multiple Regression)로 분류 할 수 있으며 각각을 또 두가지로 분류 할 수 있는데 회귀계수(기울기, x의상수값)가 선형이면 선형회귀, 비선형이면 비선형 회귀모델로 구분을 할 수 있다.

단순선형 회귀(Simple Regression)

선형회귀의 장단점

선형회귀의 장점 : 다른 ML(Machine Learning) 모델에 비해 상대적으로 학습이 빠르며 설명력이 좋다.

선형회귀의 단점 : 선형 모델의 특성상 과소적합(underfitting)이 일어나기 쉽다

회귀분석을 하는 목적

회귀분석은 독립변수로 종속변수를 찾고자 할 때 사용한다. 선형회귀는 주어져 있지 않은 점의 함수값을 보간하여 예측하는데 도움을 주며, 또한 기존 데이터의 범위를 넘어서는 값을 예측하기 위한 외삽도 제공해 준다.

기준모델(Baseline Model)

어떠한 예측 모델을 구체적으로 만들기 전에 가장 간단하면서도 직관적이면서 최소한의 성능을 나타내는 기준이 되는 모델을 기준모델이라고 한다. 회귀모델에서는 타겟이 되는 값의 평균값을 기준모델로 사용한다.(최소한 기준모델의 성능은 넘자!!!)

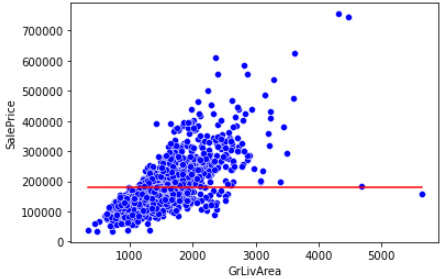
그외, 분류문제에서는 타겟의 최빈 클래스를 사용하며, 시계열회귀문제에서는 이전 타임스탬프의 값을 기준모델로 사용한다.

# predict: 기준모델인 평균으로 예측을 한다.
predict = df['SalePrice'].mean()

# 평균값으로 예측할 때 샘플 별 평균값과의 차이(error)를 저장한다.(기준모델(=예측값) - 실제값)
errors = predict - df['SalePrice']
# 절대값을 취한 후 평균으로 계산한다.
errors.abs().mean()

Simple Linear Regression만들기

## Scikit-Learn 라이브러리에서 사용할 예측모델 클래스를 Import 합니다
from sklearn.linear_model import LinearRegression

## 예측모델 인스턴스를 만듭니다
model = LinearRegression()

# 특성과 타겟값을 feature,target에 넣고 데이터를 만들어줍니다.
X_train = df[feature]
y_train = df[target]

## 모델을 학습(fit)합니다
model.fit(X_train, y_train)

## 새로운 데이터 한 샘플을 선택해 학습한 모델을 통해 예측해 봅니다
X_test = [[4000]]
y_pred = model.predict(X_test)

print(f'{X_test[0][0]} sqft GrLivArea를 가지는 주택의 예상 가격은 ${int(y_pred)} 입니다.')
>>> 4000 sqft GrLivArea를 가지는 주택의 예상 가격은 $447090 입니다.

# 계수(coefficient)
model.coef_
>>> array([[107.13035897]])
# 절편(intercept)
model.intercept_
>>> array([18569.02585649])

mean_absolute_error(MAE,평균절대오차)

줄여서 MAE라고 부르는 이것은 모델의 평가지표중 하나로서 모델의 예측값과 실제값의 차이의 절대값을 모두 더한 개념이다.

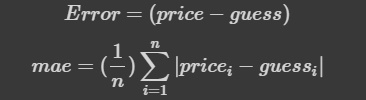
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error

y_train = train[target]
y_test = test[target]

# 기준모델을 평균으로
predict = y_train.mean()

# 기준모델로 훈련 에러(MAE)계산
# 기준모델과 y_train의 MAE평가지표를 활용하여 오차 계산하기
y_pred = [predict] * len(y_train)
mae = mean_absolute_error(y_train, y_pred)

예측모델(Predictive Model)활용하기

기준모델에서 보여진 scatterplot에 가장 잘맞는 직선을 그려주는 것이 회귀의 예측모델이다.

이때 잔차(residual)가 활용된다.
예측값은 만들어진 모델이 추정하는 값을 뜻하며, 잔차는 예측값과 관측값의 차이이다.

그림에서 보여지는 회귀선은 잔차제곱들의 합인(RSS,residual sum of squares)를 최소화 하는 직선이다(RSS는 SSE라고도 한다). 이 값이 회귀모델의 Cost function(비용함수)가 된다.

머신러닝에서는 이렇게 Cost function을 최소화 하는 모델을 찾는 과정을 학습한다라고 부른다.

${\displaystyle \operatorname {RSS} =\sum _{i=1}^{n}(y_{i}-(\alpha x_{i} + \beta))^{2}}$

위의 식이 잔차제곱의 함 RSS이며.
관측값 - 예측값(ax+B의 제곱)이다.

즉, 알파 값과 베타값이 최소화 되는 모델을 찾는것이다.

이렇게 잔차제곱합을 최소화 하는 방법을 최소제곱회귀 혹은 OLS회귀 라고 부른다.

잔차제곱의 합(RSS)를 최소화 하는 회귀계수와 y절편 찾기

첫 번째, sklearn으로 하는방법.

from sklearn.linear_model import LinearRegression

## 예측모델 인스턴스를 만든다
model = LinearRegression()

# train데이터를 설정한다
X_train = df[feature]
y_train = df[target]

## 모델을 학습(fit)한다
model.fit(X_train, y_train)

# 계수를 찾는 함수를 입력한다.
model.coef_
>>> (회귀계수가 출력이된다.)
(이때 출력되는 회귀계수는 잔차제곱의합(RSS)가 최소가 될때의 회귀계수이다.

# y절편값을 찾는 함수를 입력한다.
model.intercept_
>>> (절편값이 입력된다.)

두 번째, statsmodel로 하는 방법.

# 먼저 모델을 다운로드 한다.
pip install statsmodels

# 모델을 import한다
import statsmodels.api as sm

# 모델을 사용하여 출력한다.
lm = sm.OLS(df[target], df[[feature]])
results = lm.fit()
results.summary()
>>> (결과 표가 출력이 된다.)

저는 이렇게 feature를 두개로 예시를 들어보았다.

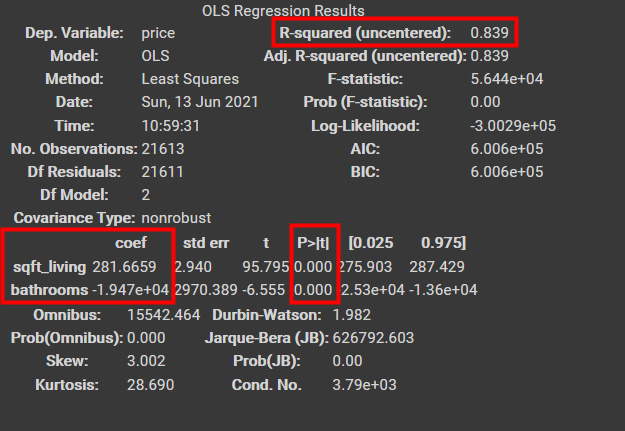
결과값은 다음과 같이 나타나며 여기서 확인해야 우선적으로 확인해야 할것은 다음과같이 사각형으로 표시해둔 부분다.

coef는 회귀계수를 의미합니다.
즉 sqft_living의 경우 281.6659X라고 보면된다.

다음 옆으로 가면 P값이 있다. 즉, 둘다 통계적으로 유의하다는 것을 알 수 있다.

위에 보면 R-squared라고 되어있는것이 있다. 이것은 결정계수(coefficient of determination)을 의미한다. 자세한것은 아래에서 다루겠다.

R-squared

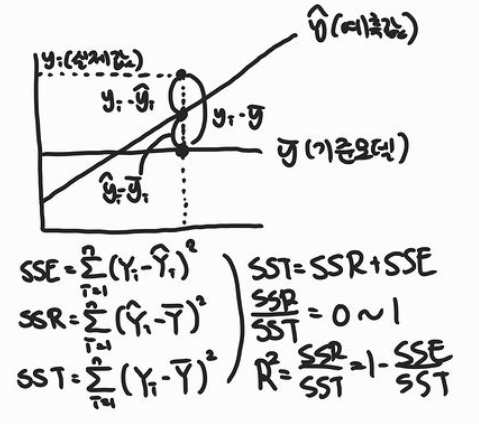
R-squared는 현재 사용하고 있는 x변수가 y변수의 분산을 얼마나 줄였는가 입니다.
단순히 y평균값 모델(기준모델)을 사용했을때 대비 우리가 가진 x변수를 사용함으로서 얻는 성능 향상의 정도이다.

즉, R-squared 값이 1에 가까우면 데이터를 잘 설명하는 모델이고 0에 가까울수록 설명을 못하는 모델이라고 생각할 수 있다.

다중선형회귀(Multiple Regression)

다중선형회귀의 경우 말그대로 feature가 2개 이상일때를 다중선형회귀라고 부른다.

# 다중모델 학습을 위한 feature설정
features = ['GrLivArea', 
            'OverallQual']
X_train = train[features]
X_test = test[features]

# 모델 fit
model.fit(X_train, y_train)
y_pred = model.predict(X_train)
mae = mean_absolute_error(y_train, y_pred)

다중 선형회귀의 경우 1개의 특성(feature)를 사용 했을 때 보다 더 좋은 성능을 낼 수 있다.

실제로 단순선형회귀를 쓰는경우는 많이없다 왜냐하면 더 좋은모델이 많기 때문이다. 하지만 장단점이 있기에 무조건 쓰지 않는것은 아니며 앞으로 다른모델을 이해하는데 바탕이 되므로 학습을 할것이다.

하지만 디테일한 학습에 있어서는 다중선형회귀에 더 집중할것이고 그중에서 릿지나 나쏘회귀에 더 집중을 할 것이다.