클러스터링(군집화) 정리

생각하는 마리오네트·2021년 11월 8일

목록 보기

9/9

INDEX

목적

종류

similarity

종류 1 : 계층군집

종류 2 : PointAssignment(K-means)

계층군집과 PointAssignment(K-means)의 장단점

내가 클러스터링을 공부하면서 겪었던 개념적 착오 정리

군집분석 단계

최적의 군집갯수 구하는 방법

군집평가(Cluster Evaluation)

계층군집 예시

목적

주어진 데이터들이 얼마나 어떻게 유사한지
주어진 데이터셋을 요약, 정리하는데 매우 효율적인 방법 중 하나.
but, 정답을 보장하지 않기 때문에 예측을 위한 모델링 보다는 EDA를 위해 많이 사용된다.
또한 클러스터링은 비지도 학습 알고리즘의 하나인 군집화의 기능적 의미는 숨어있는 새로운 집단을 발견하는 것입니다. 새로운 군집 내의 데이터 값을 분석하고 이해함으로서 이 집단에 새로운 의미를 부여할 수 있고 전체 데이터를 다각도로 살펴볼 수 있다.

종류

Hierarchical(계층군집) : 모든 관찰치는 자신만의 군집에서 시작하여 유사한 데이타 두 개를 하나의 군집으로 묶는데 이를 모든 데이타가 하나의 군집으로 묶일때까지 반복한다. 알고리즘은 다음과 같다.

1. 모든 관찰치를 군집으로 정의한다.
2. 모든 군집에 대하여 다른 모든 군집과의 거리를 계산한다.
3. 가장 작은 거리를 갖는 두 군집을 합해 하나의 군집으로 만든다. 따라서 군집의 갯수가 하나 감소한다.
4. 2와3을 반복하여 모든 관찰치가 하나의  군집으로 합쳐질 때까지 반복한다.

o Agglomerative(합병) : 개별 포인트 에서 시작후 점점 크게 합쳐감.
o Divisive(분할) : 한 개의 큰 cluster에서 시작 후 점점 작은 cluster로 감

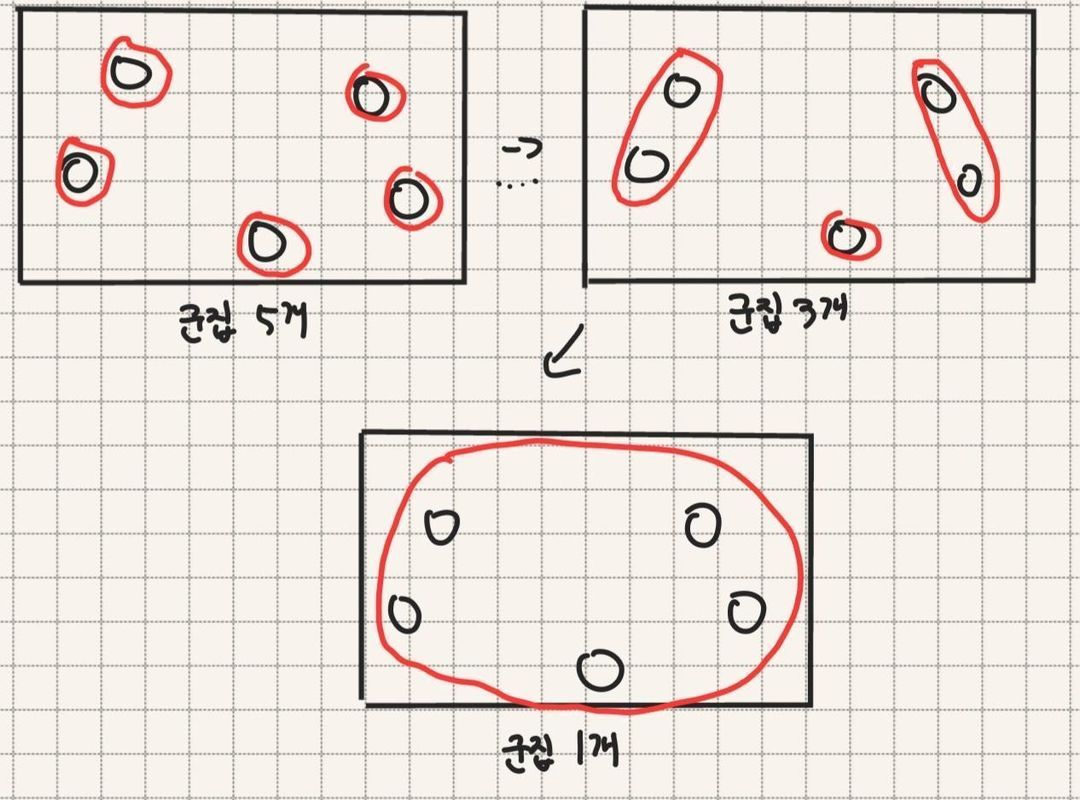
Point Assignment(분할군집) : 분할군집에서는 먼저 군집의 갯수 K 를 정한 후 데이터를 무작위로 K개의 군으로 배정한 후 다시 계산하여 군집으로 나눈다. k-means clustering과 PAM을 다룬다.
- 가장 많이 사용하는 것은 k-means이고 알고리즘은 다음과 같다.

1. K개의 centroids를 선택한다.(K개의 행을 무작위로 선택)
2. 각 데이터를 가장 가까운 centroid에 할당한다.
3. 각 군집에 속한 모든 데이타의 평균으로 centroid를 다시 계산한다.(즉, centroid는 p-개의 길이를 갖는 평균벡터로 p는 변수의 수이다.)
4. 각 데이터를 가장 가까운 centroid에 할당한다.
5. 모든 관측치의 재할당이 일어나지 않거나 최대반복횟수(R에서의 dafault값은 10회)에 도달할 때까지 3과 4를 반복한다.

Similarity(거리, 유사도)

두 샘플이 유사하다 = 두 샘플간 유사도가 높다 = 두 샘플간 거리가 짧다
반드시 similarity를 측정하기 전 수치형 변수로 만들어야 한다. -> 거리,유사도 척도는 수치형 변수에 대해 정의되어 있기 때문이다.

1. Euclidean(유클리디안 거리)

- 가장 흔하게 사용되는 거리 척도로 빛이 가는 거리로 정의

2. 맨하탄 거리

- 정수형 데이터(예:리커트 척도(설문조사))에 적합한 거리척도
- 수직, 수평으로만 이동한 거리의 합으로 정의됨.

3. 코사인 유사도

- 스케일을 고려하지 않고 방향 유사도를 측정하는 상황(예 : 상품 추천)에 주로 사용.

4. 매칭 유사도

- 이진형 데이터에 적합한 유사도 척도로 전체 특징 중 일치하는 비율을 고려함.

X1	X2	X3	X4	X5
1	0	1	0	0
0	0	1	0	1

- 위와 같은 경우 $3/5$

5. 자카드 유사도

- 이진형 데이터에 적합한 유사도 척도로 둘 중 하나라도 1을 가지는 특징 중 일치하는 비율을 고려함

X1	X2	X3	X4	X5
1	0	1	0	0
0	0	1	0	1

- 위와 같은 경우 1/3
- 희소한 이진형 데이터에 적합한 유사도 척도됨(ex> 둘다 1이 나올경우가 희박할때)

계층군집(Hierarchical)

sklearn.cluster.AgglomerativeClustering

 1. n_clusters : 계층군집에서 해당 파라미터는 몇개의 
 군집으로 할것이냐를 설정하는것이라고 생각하면 옳지않다. 
 계층군집은 k-means와 다르게 k값을 사전에 설정하지 않는 
 특징을 가지고 있다. 또한 군집이 1개가 될때까지 진행한다.
 따라서 해당 파라미터는 early stop같은  기능이라고 보면된다. 
 즉, 2를 설정하면 2개를 최종1개로 합쳐 지기전에 2개까지 만
 계층군집시키는것을 뜻한다.
 
 2. affinity : 거리척도(Euclidean, manhattan, cosine, precomputed)
      - linkage가 ward인 경우 Euclidean만 사용가능
      - precomputed는 거리 혹은 유사도 행렬을 입력으로 하는 경우에 설정하는값
 
 3. linkage : 군집간 거리(ward, complete, average, single)
 
    * ward (와드 연결법 : 가장 많이 쓰인다.)
    모든 변수들에 대하여 두 군집의 ANOVA sum of square를 더한 값
    1. 이상치에 매우둔감
    2. 계산량이 매우 많음
    3. 군집크기를 비슷하게 만듦( 해석이 더 편하고 이상적이다.)
    
    
    * complete(최장 연결법)
    한 군집의 점과 다른 군집의 점 사이의 가장 긴 거리(longest distance)
    1. 이상치에 민감
    2. 계산량이 많다.
    
    * average(평균연결법,single과 complete의 절충)
    한 군집의 점과 다른 군집의 점 사이의 평균 거리.
    1. 이상치에 둔감
    2. 계산량이 많은편
    
    * single(최단연결)
    한 군집의 점과 다른 군집의 점 사이의 가장 짧은 거리
    1. 이상치에 민감
    2. 계산량이 많은편
    
4. fit(x) : 데이터 x에 대한 군집화 모델 학습
5. fit_predict(x) : 데이터 x에 대한 군집화 모델학습 및 라벨 반환
6. labels_ : fitting한 데이터 샘플들이속한 군집 정보

실습

from sklearn.cluster import AgglomerativeClustering as AC 
clusters = AC(n_clusters = 3,
              affinity = 'euclidean',
              linkage = 'ward')
              
clusters.fit(df)       
#clusters.labels_ >> array([2, 0, 2, ..., 2, 2, 1])
df['군집소속'] = clusters.labels_
df['군집소속']

>>>
output

0       2
1       0
2       2
3       0
4       2
       ..
7038    0
7039    1
7040    2
7041    2
7042    1

K-means 군집화

1) k 개의 중심점 설정
2) 샘플 할당
3) 중심점 업데이트를 반복하는 방식으로 k개의 군집을 생성하는 알고리즘
4) 정리 : 군집의 중심점(centroid)이라는 특정한 임의의 지점을 선택하여 해당 중심에 가장 가까운 포인트들을 선택하는 군집화 기법으로서, 군집중심점은 선택된 포인트의 평균지점으로 이동하고 이동된 중심점에서 다시 가까운 포인트를 선택, 다시 중심점을 평균지점으로 이동하는 프로세스를 반복적으로 수행한다. 이때, 모든 데이터포인트에서 더이상 중심점의 이동이 없을 경우에 반복을 멈추고 해당 중심점에 속하는 데이터 포인트들을 군집화한다.

sklearn.cluster.KMeans

1. n_clusters : 군집 갯수
2. max_iter : 최대 이터레이션 횟수(최대 군집 시도횟수)
3. fit(X) : 데이터 x에 대한 군집화 모델 학습
4. fit_predict(X) : 데이터 x에 대한 군집화 모델 학습 및 라벨 반환
5. labels_ : fitting한 데이터에 있는 샘플들이 속한 군집 정보
6. cluster_centers_ : fitting한 데이터에 있는 샘플들이 속한 군집 중심점
7. init : 최초의 중심점 설정('k-means++' 를 보통 사용한다.)

실습

from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters =3, init = 'k-means++', max_iter =300, random_state = 42)

kmeans.fit(df)

df['군집소속'] = kmeans.labels_
df['군집소속']
>>>
output
0       1
1       1
2       1
3       1
4       1
       ..
7038    0
7039    2
7040    1
7041    1
7042    2

장단점

	장점	단점
계층군집화	1. 덴드로그램을 이용한 군집화 과정 확인 가능(데이터가 크지않을때) 2. 거리/유사도 행렬만 있으면 군집화 가능 3. 다양한 거리 척도 활용가능 4. 수행할 때 마다 같은 결과를 냄(임의성 존재x)	1. 상대적으로 많은 계산량 -> 상대적으로 데이터 크기가 작은 문제에 적용된다. 2.군집개수 설정에 대한 제약 존재
PointAssignment(K-means)	1. 상대적으로 적은 계산량, 2. 군집 개수 설정에 제약이 없고 쉬움, 3. k평균알고리즘은 각 유형을 나눌때 사용한 k개의 중심점이 곧 해당 유형의 대표값이기 때문에 각 유형의 특징을 파악하기 쉽다.	1. 초기 중심설정에 따른 수행할때마다 다른결과를 낼 가능성 존재(임의성 존재ㅇ) 2. 데이터 분포가 특이하거나 군집별 밀도 차이가 존재하면 좋은 성능을 내기 어려움 3. 유클리디안 거리만 사용해야함(중심점이 있기때문) 4. 수렴하지 않을 가능성 존재 5. 속성개수가 많으면 군집화 정확도가 떨어진다. 5. 반복횟수가 많으면 속도가 매우 느려진다.

내가 클러스터링을 공부하면서 겪었던 개념적 착오 정리

k-means클러스터링이 k개를 사전에 지정해줄수 있는 점에서 계층군집화랑 다르다고 했는데, 계층군집화에서도 n_clusters파라미터가 있어서 "둘다 k개를 사전에 지정해주네??" 라고 생각을 하여 언제 어떤 군집방법을 사용해야하는지에 대한 어려움을 겪었다. 구글링과 커뮤니티를 돌아다니며 끝까지 알고자 노력한 결과 계층군집화의 n_clusters는 사전에 클러스터군집화를 설정해준다기 보다는 early stop과 같은 기능인것이다. 즉, 한개의 군집으로 묶이기전에 필요한 군집 갯수에서 멈추는 것이다. 이렇게하여 각 방법의 파라미터 차이를 이해하게 되었다.
k-means의 경우 엘보메소드, 실루엣스코어 등 다양한 방법으로 시각화가 가능하고 증명이가능하지만 계층군집의 경우 덴드로그램만 사용하는데 이를 통해 어떻게 군집화가 잘되었는지 확인을 할 수 있을지에 대한 의문이 있었다. 하지만 여기서 중요한것은 군집화는 비지도 학습이기 때문에 정답이 있지않다. 즉, 덴드로 그램을 보고 어떻게 군집화가 되고있는지 그 과정을 보기위함이 더 큰 이유였고, eda나 분석가의 목적 및 판단에 따라 중간에 군집갯수를 조정하면 된다는 점이다.
그리고, 좋은 클러스터링은 군집내 분산은 작고 군집간 분산이 큰것으로 짐작해볼수 있다.
만약에 계층군집으로 무조건 시각화를 해야한다면 차원을 줄여서 시각화 (UMAP, t-SNE)해본 다음 군집화가 잘되었는지 눈으로 확인 해봐도된다.
정리를 해보면, 계층적 군집분석은 군집의 개수를 정확하게 결정하는것이 목적이 아니다. 일반적으로 계층군집을 먼저수행할때가 있는데 이유는 데이터 군집형성이 어떻게 이루어졌는지 확인하는 목적이강하다. 이때 연구자의 판단과 경험에 비추어 적절한 수준의 군집의 갯수를 예측하게 되며, 관찰값들이 어떤 모양으로 군집을 이루고 있는지 확인하게 된다. 한번 합병되면 다신 분리되지 않는 성질을 가지고 있기 때문에 형성된 군집이 의미가 있는지 검토할 필요가 있다. 가능하다면 여러가지 다양한방법으로 군집을 형성해 보고 결정하는것이 좋다. 결론은 클러스터링 할때 너무 정답에 집착하지 말아야한다. p-value와 같은 내용이 없기 때문에 판단하기 쉽지않으며 다양한 방법을 적용하여 결과의 일치성을 보면서 기존의 분석과 비교하거나 논리적으로 설명 가능한 결과를 보고자 노력해야 한다.

군집분석 단계

1. 알맞은 속성 선택(데이터를 군집화하는데 중요하다고 생각하는 특성들을 선택하는 단계)

이 단계는 군집화할 대상이 어떤 특성들로 군집화 되기를 원하는지에 따라 
도메인에 따라 혹은 분석가의 목적에 따라 다를 수 있다.하지만, 아무리 복잡하고 
철저하게 군집분석을 하더라도 잘못된 특성을 넣게되면 좋은 결과를 얻지 못할수 
있다.

예시>

모든 특성을 군집화 시켰을때

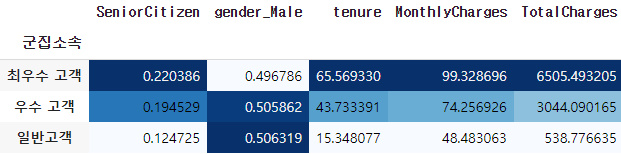
특정한 특성을 군집화 시켰을때

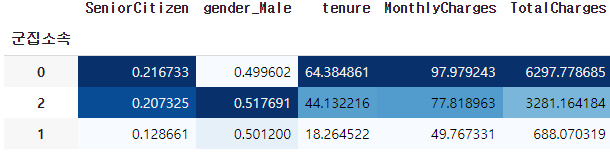
위의 두가지 경우는 모든 특성과 특정 특성을 군집화시켰을때의 결과이다. 두번째 표의 군집소속은 위에서부터 최우수,우수,일반고객이다.
특정한 특성을 넣었을때에도 데이터에 가장 중요한 요소들로 구성을 선택하였기 때문에 크게 차이가 있지는 않다. 하지만 좀더 정확하고 특성이 중요도를 구분하기 힘든경우 차이가 많이 날 수 있기때문에 분석에 맞는 특성을 고르는것과 맞지않는 특성을 배제시키는것은 중요하다.
저의경우 비용을 많이 지출한 고객과 상대적으로 적게 지출한 고객을 분석하는것이 핵심이었기 때문에 "가입기간", "월요금", "총요금" 이렇게 세가지를 선택하였습니다

2. 데이터 스케일링(분석에 사용되는 변수들의 범위에 차이가 있는경우 범위가 가장 큰 변수가 가장 큰 영향을 미치게 되므로 데이터 스케일을 맞추어 줘야하며 이때는 평균0, 표준편차1인 표준화를 가장많이 사용한다)

표준화를 시켜주었습니다.

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
data[['tenure', 'MonthlyCharges', 'TotalCharges']] = scaler.fit_transform(data[['tenure', 'MonthlyCharges', 'TotalCharges']])
data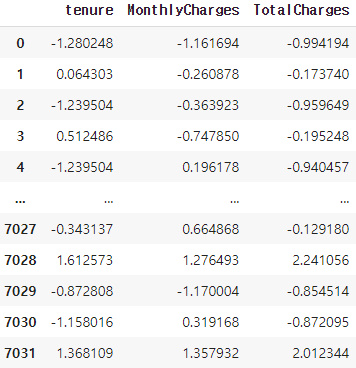

3. 이상치 제거

표준화를 해주어서 그런지 이상치가 없었습니다.

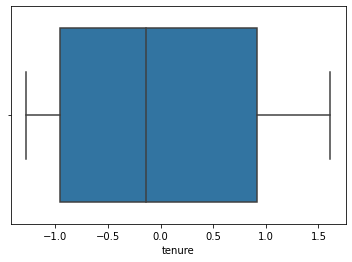
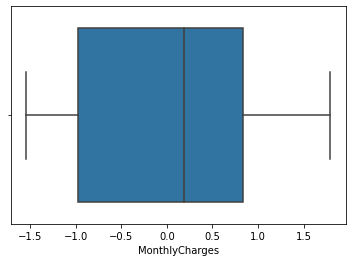
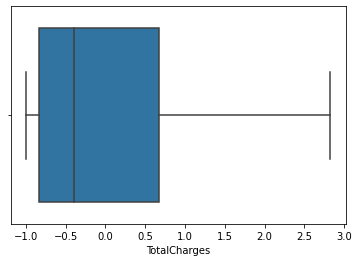
5. 군집 알고리즘 선택하기

이번 데이터의 경우 k-means를 선택하게 되었는데 그 이유는 먼저 목적이 오랜기간가입한 고객이면서 월요금,총요금이 높은 수익을 안겨준 기준으로 우수고객과 그렇지 않은 고객을 군집하는것이기 때문에 최우수,우수,일반고객 혹은 우수,일반고객 으로 k를 3개 혹은 2개중에서 생각하고 있었기 때문에 사전에 최적의 k값을 구하게 되므로 비계층군집방법인 k-means를 사용하였다.
또한 계층군집처럼 덴드로그램을 이용하여 어떻게 군집이 이루어지는지 확인할 필요가 없으므로 계층군집을 이용할 필요는 없다.

6. 군집분석 결과를 얻기

2개 혹은 3개를 입력해 보고 어떻게 형성되는지 1차적으로 확인하는 단계이다.

7. 군집의 갯수 결정

최적의 군집갯수를 구하는 단계이다.
비계층군집의 경우 "Elbow Method" 혹은 "silhouette_score(실루엣점수)"를 통해 최적의 군집을 구할 수 있다.
Elbow Method

from sklearn.cluster import KMeans
sum_of_squared_distances = []
K = range(1, 15)
for k in K:
    km = KMeans(n_clusters = k)
    km = km.fit(data)
    sum_of_squared_distances.append(km.inertia_)
    
# 시각화

plt.plot(K, sum_of_squared_distances, 'bx-')
plt.xlabel('k')
plt.ylabel('Sum_of_squared_distances')
plt.title('Elbow Method For Optimal k')
plt.axvline(2,c= 'r',alpha =0.4)
plt.axvline(3,c= 'r',alpha =0.4)
plt.show()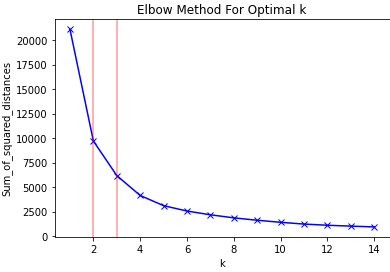

Elbow Method는 2개에서 3개가 최적으로 보인다.

silhouette_score(실루엣점수)

실루엣 분석은 각 군집간의 거리가 얼마나 효율적으로 분리되어 있는지를 나타낸다.(효율적으로 잘 분리 되어있다 = 다른 군집과의 거리는 떨어져 있고, 동일 군집끼리 데이터는 서로 가깝게 뭉쳐있다는 의미)

-1에서 1사이의 값을 가지며, 1에 가까울수록 근처의 군집과 멀리 떨어져있는 것이며 0에 가까울 수록 근처 군집과 가깝다는 뜻이다 즉, 1에 가까울수록 좋은것이다.

from sklearn.metrics import silhouette_score
k_range = range(2,14)

best_n = -1
best_silhouette_score = -1

for k in k_range:

  kmeans = KMeans(n_clusters=k, random_state=200)
  kmeans.fit(data)
  clusters = kmeans.predict(data)

  score = silhouette_score(data, clusters)
  print('k :',  k, 'score :', score)

  if score > best_silhouette_score:
    best_n = k
    best_silhouette_score = score

print('best n :', best_n, 'best score :', best_silhouette_score )

>>>

k : 2 score : 0.4795243516623505
k : 3 score : 0.45162348516961115
k : 4 score : 0.4720646569227696
k : 5 score : 0.44345410777667377
k : 6 score : 0.43857106174593297
k : 7 score : 0.4326261790305853
k : 8 score : 0.42735399053894063
k : 9 score : 0.4304872121034563
k : 10 score : 0.4356814188700147
k : 11 score : 0.4292963170580597
k : 12 score : 0.43024127046747296
k : 13 score : 0.42545018406902924
best n : 2 best score : 0.4795243516623505

실루엣점수는 k가 2개일때 가장 좋은 점수를 보여줍니다. (실루엣점수가 1에 가까울 수록 군집화가 적절히 되었다.

2개의 평가 결과 k가 2개인경우가 적절하다고 판단을 내려볼 수 있다.

8. 결정한 갯수를 입력한 최종결과 얻기

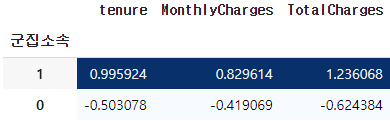
아래는 군집한 결과로 groupby 한 것이다.
1번 군집이 0번보다 높은것으로 보아 우수고객으로 설정하면 될것같다.
하지만 여기서 표준화를 시켜주었기 때문에 해당 자료로 해석하기 힘들다.
따라서 이를 해석하는 것은 10번에서 다루어 보겠다.

9. 분석 결과 시각화

3차원 시각화

from mpl_toolkits.mplot3d import Axes3D


fig = plt.figure( figsize=(6,6))
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=15, azim=170)
ax.scatter(data['tenure'],data['MonthlyCharges'],data['TotalCharges'],c=data['군집소속'],alpha=0.5)
ax.set_xlabel('tenure')
ax.set_ylabel('MonthlyCharges')
ax.set_zlabel('TotalCharges')

plt.show()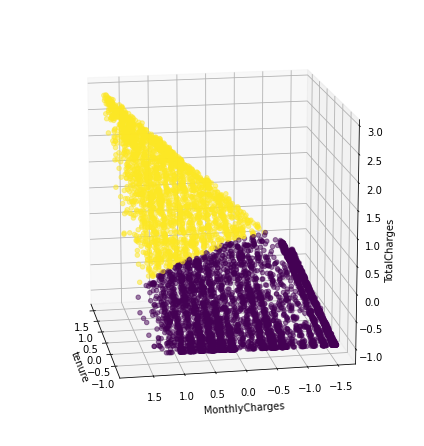

노란색이 우수고객, 보라색이 일반고객이다. 데이터를 살펴보면
기간기 길고, 월요금이 많고, 총요금이 높은구간으로 갈수록 노란색으로 바뀌는
것을 볼 수 있다.

2차원 시각화
3차원 시각화가 이해가 잘 안될 수 있기때문에 차원축소를 통해 2차원 평면을통해 그려보았습니다.

# 차원축소
from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
pca_transformed = pca.fit_transform(data)

# 2차원 데이터를 테이블에 삽입
data['pca_x'] = pca_transformed[:,0]
data['pca_y'] = pca_transformed[:,1]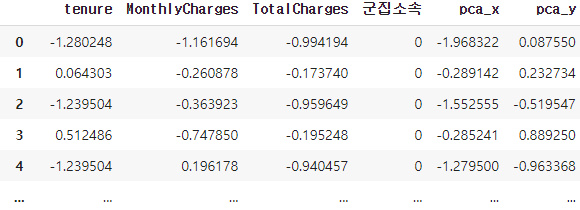

# 군집값이 0,1인 경우 별도 인덱스 추출
marker0_ind = data[data['군집소속']==0].index
marker1_ind = data[data['군집소속']==1].index

# 군집 값 0,1에 해당하는 인데스로 각 군집 레벨의 pca_x, pca_y값 추출
plt.scatter(x = data.loc[marker0_ind,'pca_x'], y = data.loc[marker0_ind, 'pca_y'], marker = 'o')
plt.scatter(x = data.loc[marker1_ind,'pca_x'], y = data.loc[marker1_ind, 'pca_y'], marker = 's')

plt.xlabel('PCA 1')
plt.ylabel('PCA 2')
plt.title('2 Clusters Visualizatino by 2 PCA Components')
plt.show()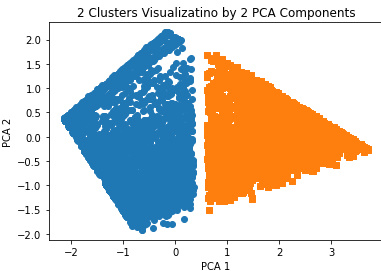

군집화가 잘 되어보이는 시각화결과를 3d와 2d로 각각 나타내었습니다.

10. 군집분석 결과 해석하기 및 활용하기

군집화한것을 특성을 뽑기전 테이블과 합쳐서 의미를 이끌어내 보았습니다.(길기때문에 중간에 잘랐습니다.)

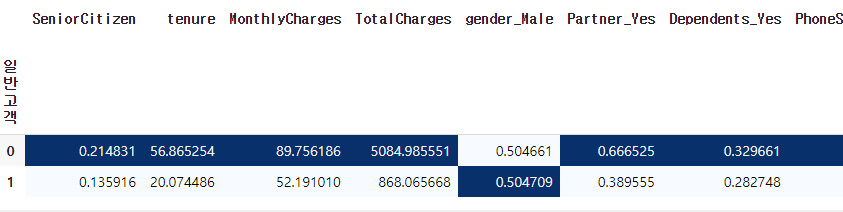
일반고객여부(0은 우수고객, 1은일반고객)에 따른 데이터입니다. 우수고객은 사용기간의 평균이 56, 월요금이 89, 총요금이 5084정도 되는것을 알게되었습니다. 개인마다 이후 추가적인 인사이트를 얻고 또 새로운 군집과 목적에따른 다각도로 해석을 할 수 있습니다.

최적의 군집 갯수 구하기

k-means

Elbow Method : Cluster간의 거리합을 나타내는 inertia가 급격하게 떨어지는 구간이 생긴다. 이 지점의 k값을 군집의 개수로 사용하며, inertia_를 통해 속성으로 확인할 수 있다.
silhouette (실루엣) : 군집타당성 지표라고 불리는 실루엣 점수를 이용하여 구할 수 있다. 1에 가까울 수록 적절한 군집화가 되었다고 판단할 수 있다.

AgglomerativeClustering

silhouette (실루엣) : 군집타당성 지표라고 불리는 실루엣 점수를 이용하여 구할 수 있다. 1에 가까울 수록 적절한 군집화가 되었다고 판단할 수 있다.

두가지 방법모두 위의 예제에서 다 사용을 했기때문에 참고하면된다.

군집평가(Cluster Evaluation)

군집을 평가하는 방법에는 "Silhouette (실루엣)"을 통한 평가방법이 있다. 이는 위에서 다루었지만 평가를 위해 한번더 확인하고자 한다.
k-means Silhouette

from sklearn.metrics import silhouette_score
k_range = range(2,14)

best_n = -1
best_silhouette_score = -1

for k in k_range:

  kmeans = KMeans(n_clusters=k, random_state=200)
  kmeans.fit(data)
  clusters = kmeans.predict(data)

  score = silhouette_score(data, clusters)
  print('k :',  k, 'score :', score)

  if score > best_silhouette_score:
    best_n = k
    best_silhouette_score = score

print('best n :', best_n, 'best score :', best_silhouette_score )

>>>
k : 2 score : 0.4795243516623505
k : 3 score : 0.45162348516961115
k : 4 score : 0.4720646569227696
k : 5 score : 0.44345410777667377
k : 6 score : 0.43857106174593297
k : 7 score : 0.4326261790305853
k : 8 score : 0.42735399053894063
k : 9 score : 0.4304872121034563
k : 10 score : 0.4356814188700147
k : 11 score : 0.4292963170580597
k : 12 score : 0.43024127046747296
k : 13 score : 0.42545018406902924
best n : 2 best score : 0.4795243516623505

위와같이 최고의 군집은 0.47로 1에 가장가까운 수치가 선정이되었고 이때 k값은 2이다.

Hierarchical Clustering(계층군집)
계층군집의 경우 거리 방법에 따라서 구해보고 결정을 해볼 수 있다.

# single을 이용한 경우
from sklearn.cluster import AgglomerativeClustering
from sklearn.metrics import silhouette_score

k_range = range(2,14)
for k in k_range:
  single_clustering = AgglomerativeClustering(n_clusters = k, linkage = 'single')
  single_cluster = single_clustering.fit_predict(data2)
  score = silhouette_score(data2, single_cluster)
  print(score)
  
>>>
 0.0044341899920526525
-0.021597968263582904
-0.03704507789601811
-0.17676023330262106
-0.3423133163315203
-0.35861897286914585
-0.36691980982482825
-0.3745611929780066
-0.3978573444754334
-0.41813900225000206
-0.4339283820274371
-0.4389509920396276

#average거리 결과
0.4635238877116834
0.41542636175884295
0.3501228693103544
0.397905366416994
0.3950393977721433
0.4107031120958451
0.3971372420702398
0.35149898667775886
0.3472984871067392
0.3740776915661358
0.36942242501074074
0.360173775013092

# complete거리 결과
0.42522881104323185
0.3662652591400807
0.3851673666950573
0.4249555611938816
0.41874702133466624
0.39616677206362394
0.38375171943321706
0.35585765782639567
0.3151250360464463
0.31936922078274066
0.3061554889134887
0.30670387519613534

# ward거리 결과
0.42978282256466016
0.39604828114815477
0.38563910360724657
0.4061686690784082
0.4054329665900759
0.40858642796771383
0.3835451669988045
0.383199422614115
0.3854540979876939
0.38581861206088164
0.39939962561919634
0.39890202651130596

여러가지 거리를 다 확인해봤을때 k가 2일때 가장 1에 가까운것을 알수 있다.

계층군집 예시

계층군집 역시 같은 데이터로 실험해 보았습니다.

최적의 k값 구하기
계층군집의 경우 엘보메소드를 사용하지 못하기 때문에 실루엣점수로 진행했습니다.

from sklearn.cluster import AgglomerativeClustering
from sklearn.metrics import silhouette_score

# 현재 데이터에서 가장 실루엣점수가 높은 average를 사용(사전에 실험완료)
k_range = range(2,14)
for k in k_range:
  average_clustering = AgglomerativeClustering(n_clusters = k, linkage = 'average')
  average_cluster = average_clustering.fit_predict(data2)
  score = silhouette_score(data2, average_cluster)
  print(score)
  
>>>

0.4635238877116834
0.41542636175884295
0.3501228693103544
0.397905366416994
0.3950393977721433
0.4107031120958451
0.3971372420702398
0.35149898667775886
0.3472984871067392
0.3740776915661358
0.36942242501074074
0.360173775013092

실루엣점수가 1과 가장 가까운 k값2가 높은점수를 얻었습니다.

덴드로그램 시각화
계층군집화의 경우 덴드로 그램으로 시각화를 함으로서 어떻게 군집이 이루어지는지 볼 수 있습니다.

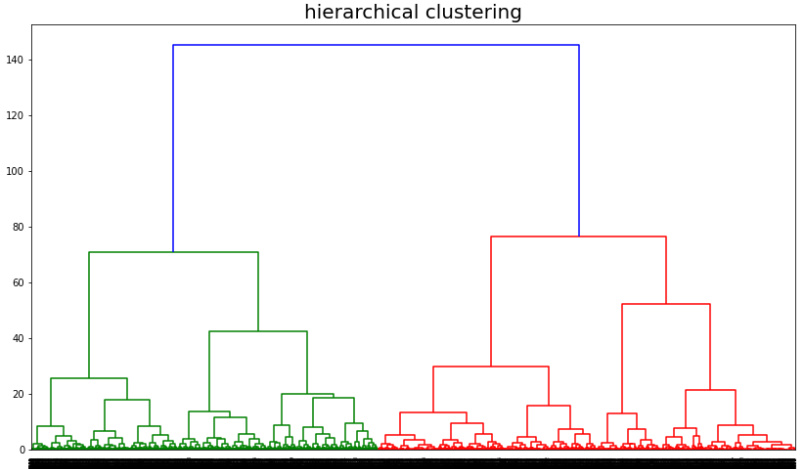
시각화를 해보니 유사도가 군집이 2개로 되었을때 비슷한 유사도 수치에서 합쳐 진것을 볼 수 있습니다.

최적의 k값 적용

from sklearn.cluster import AgglomerativeClustering as AC
clusters = AC(n_clusters = 2,
              linkage = 'average')
clusters.fit(data2)
data2['고객유형'] = clusters.labels_
data2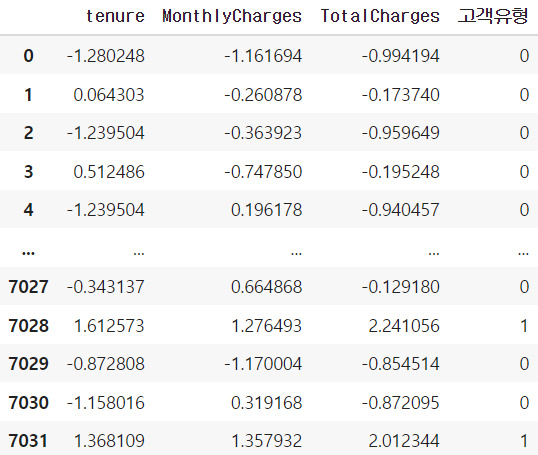

기존테이블과 merge후 군집별 데이터 수치 확인

확인결과 기간과 월지불비용, 총지불비용이 높은것은 우수고객(0), 상대적으로 작은 일반고객(1)로 되어있음을 확인할 수 있다.

생각하는 마리오네트

문제를해결하는도구로서의"데이터"

이전 포스트