https://www.youtube.com/watch?v=FhQm2Tc8Kic&t=30s
위 자료를 참고했다.
그동안 PCA의 개념은 알고있긴 했지만,
최근들어 계속 사용하면서 다시 한 번 정리해볼 필요성을 느껴 정리해보고자 한다.
차원 축소 방안
Feature Selection
- 분석 목적에 부합하는 소수의 예측변수를 선택하는 것
- 장점: 선택한 변수를 해석하기 용이하다
- 단점: 변수간 상관관계 고려가 어렵다
- Supervised feature selection
- y를 이용해 중요한 x 변수를 뽑겠다는 것
- Information gain
- Stepwise regression
- LASSO
- Genetic algorithm
...
- Unsupervised feature selection
- y 없이 x의 상관관계만으로 중요 x 변수를 뽑겠다
- PCA loading
Feature Extraction
- 예측변수의 변환을 통해 새로운 변수를 추출하는 것
- 장점: 변수간 상관관계 고려. 일반저긍로 변수의 개수를 많이 줄일 수 있다.
- 단점: 추출된 변수의 해석이 어렵다
- Supervised feature extraction
- y를 이용하되 x들의 결합으로 새로운 변수 추출
- Partial least squares (PLS)
- Unsupervised feature extraction
- y를 이용하지 않고 x들의 결합으로 변수를 뽑겠다
- Principal component analysis (PCA)
- Wavelets transforms
- AutoEncoder
PCA 개요
- 고차원 데이터를 효과적으로 분석하기 위한 대표적 분석 기법
- 차원축소, 시각화, 군집화, 압축에 사용됨
- N개의 관측치와 P개의 변수로 구성된 데이터를 상관관계가 없는 k개의 변수로 구성된 데이터로 요약하는 것
-
요약된 변수는 기존 변수의 선형결합으로 생성된다.
- 이때, "모든 X(기존변수)"의 선형결합으로 이루어지는 것
- 아래 사진에서 Z들이 추출되는 과정에 주목
- Z(주성분)은 서로 독립적이다.

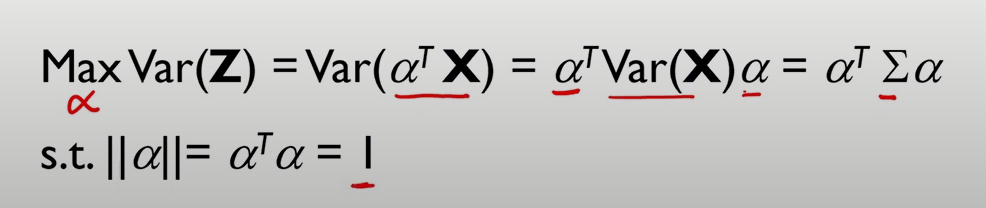
-
-
원본 데이터의 분산을 최대한 보존하는 새로운 축을 찾고, 그 축에 데이터를 Projection시키는 기법
- 예를들어, 아래와같은 두 경우가 존재할 경우 첫 번째 축이 주성분으로써 선택된다.
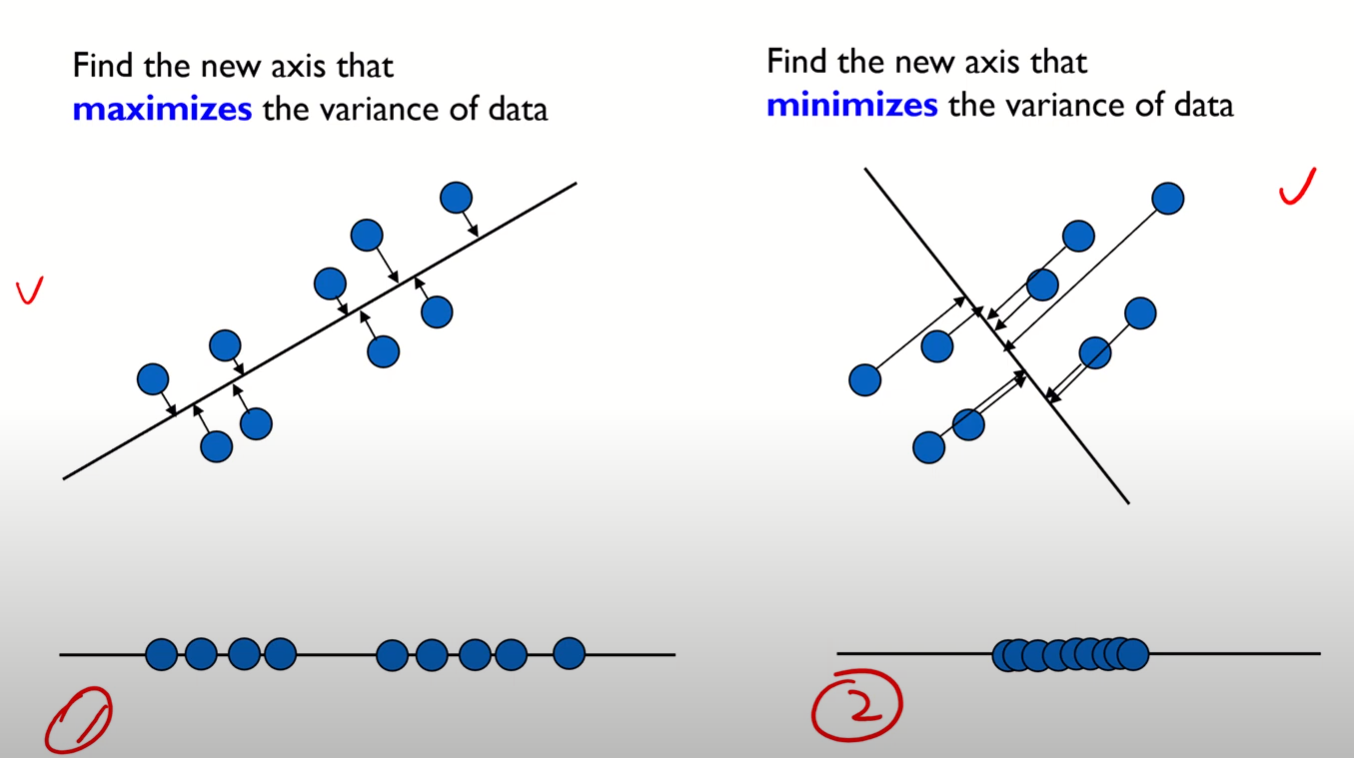
- 예를들어, 아래와같은 두 경우가 존재할 경우 첫 번째 축이 주성분으로써 선택된다.
-
일반적으로 전체 분석 과정 중 초기에 사용한다.
PCA의 수리적 배경
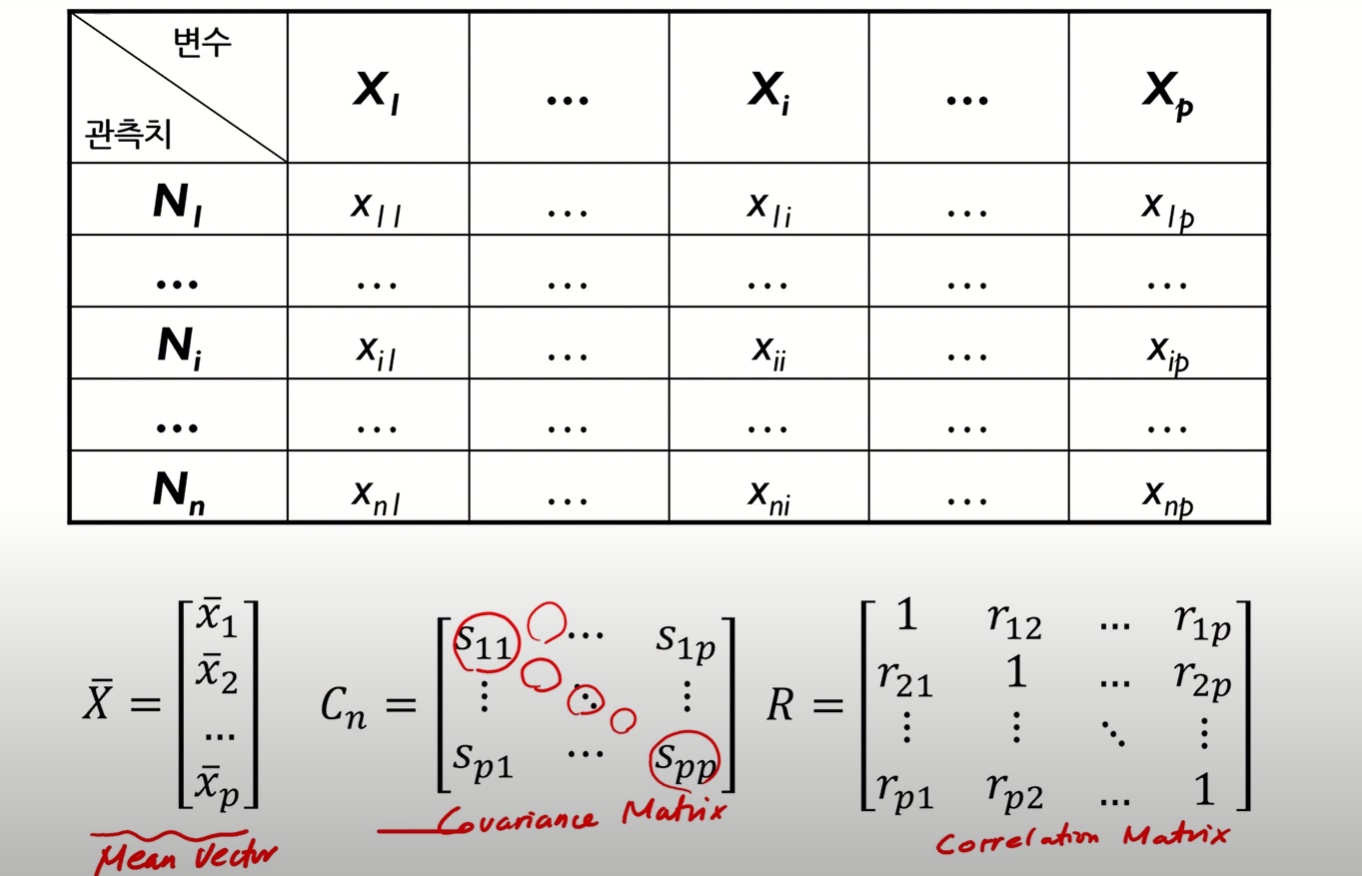
- 참고) Covariance와 Correlation과 개념은 같으나, Correlation은 Covariance의 스케일링된 버전으로 보면 된다고 한다.
- 아래 사진에서 Covariance Matrix의 대각성분은 각 변수에 대한 분산값을, 나머지에는 변수 간 공분산값을 요소로 갖는다.

Covariance Matrix Formula
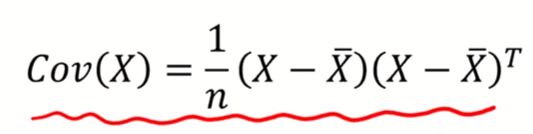
- 데이터의 총분산은 공분산행렬의 대각성분들의 합으로 표현된다.
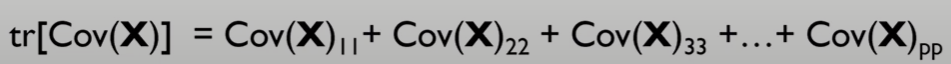
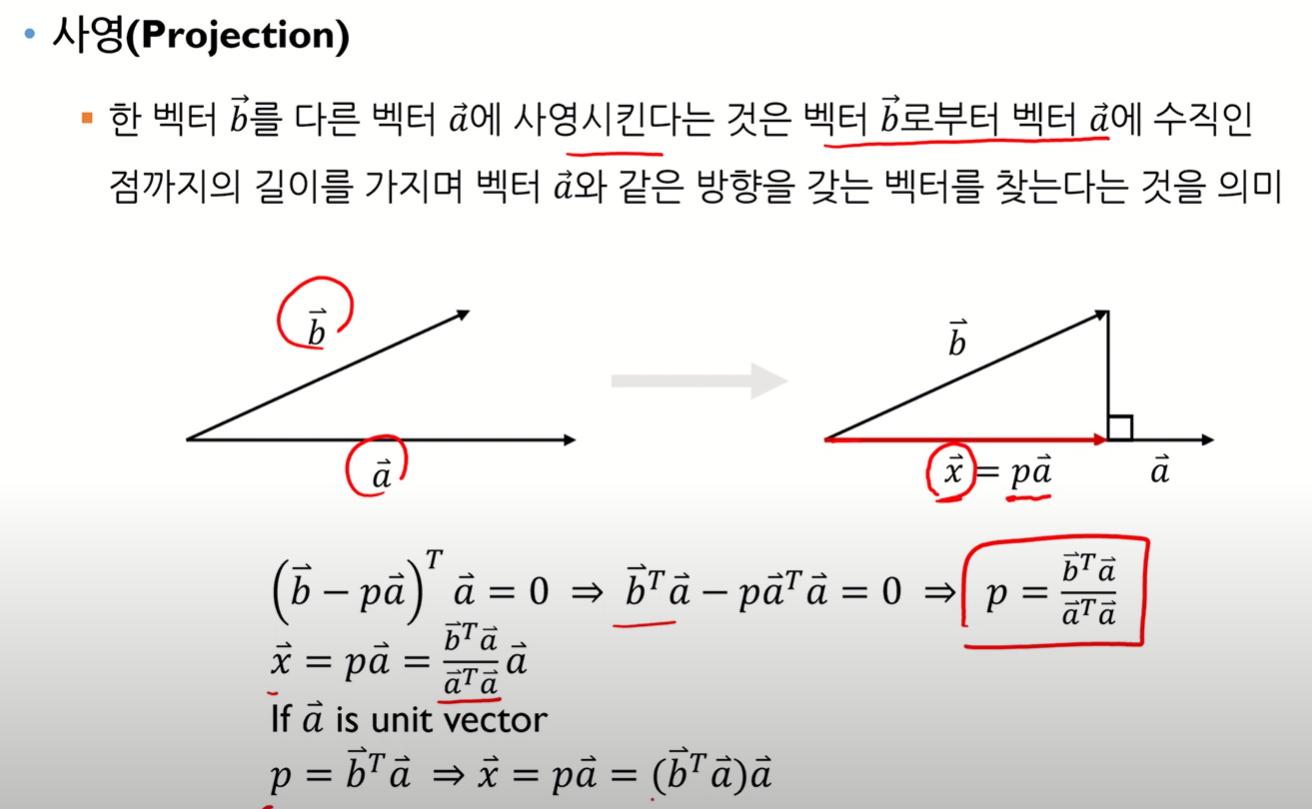
Projection
- 선형대수 공부했던 것 생각하자
Eigen value / Eigen vector
- 분명 배웠는데 정확한 개념을 설명해보라 하면 우물쭈물하게되는.. 그 개념
잘 기억해두도록 하자 - 어떤 행렬 A에 대해 상수 와 벡터 x가 다음 식을 만족할 때, 와 x를 각각 행렬 A의 EigenValue와 EigenVector라고 한다.
- A 행렬이 PxP 행렬인 경우, 해당 행렬은 P개의 Eigen value를 갖게 된다.
- 그리고, 그 Eigen value마다 벡터가 구해지는데, 이것이 Eigen vector가 되는 것
- 아래 사진에서 A가 주어진 행렬, x가 Eigen Vector, 가 Eigen Value를 의미
- Eigen Value / Eigen Vector를 구하는 자세한 매커니즘에 대해서는 따로 공부하기!
- A 행렬이 PxP 행렬인 경우, 해당 행렬은 P개의 Eigen value를 갖게 된다.

- 벡터에 행렬을 곱한다는 것을 해당 벡터를 Linear Tranformation한다는 것을 의미한다.
- 즉, 고유벡터는 해당 변환에 의해 방향이 변하지 않는 벡터를 의미한다.
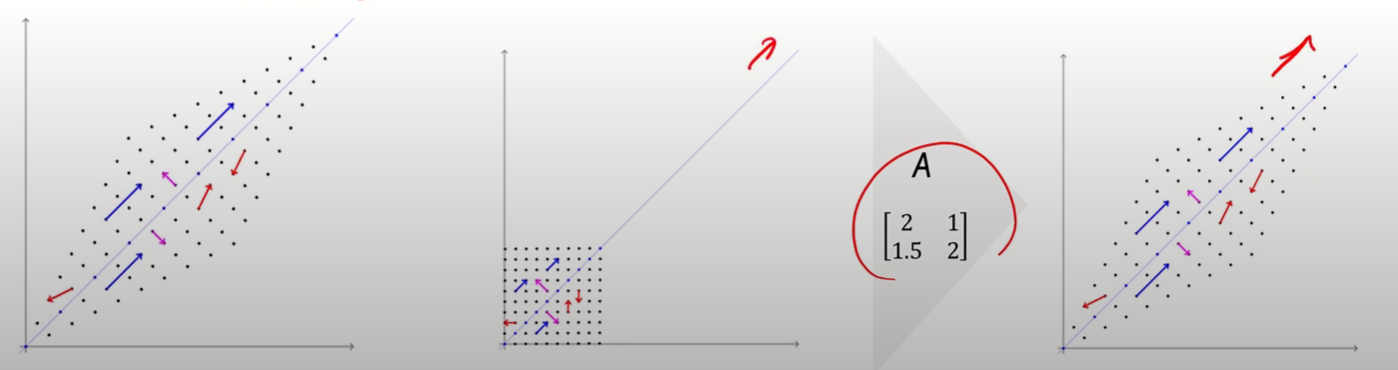
- 즉, 고유벡터는 해당 변환에 의해 방향이 변하지 않는 벡터를 의미한다.
PCA 알고리즘
-
데이터의 평균은 0이라고 가정
-
X는 pxp 크기의 공분산 행렬을 갖는 p-dimensional vector
-
는 길이 1의 p-dimensional vector
-
는 의 선형결합으로 이뤄짐
-
의 분산을 최대화하는 를 찾겠다
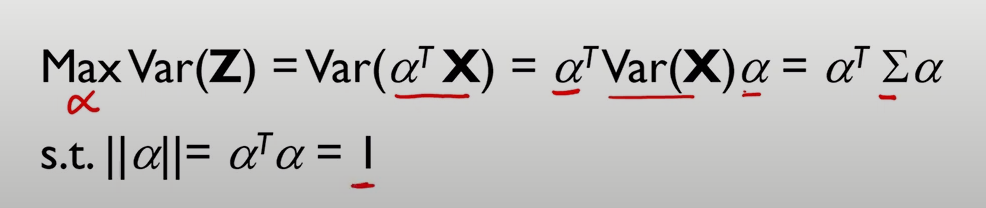
-
이때 는 공분산 행렬을 의미
-
는 eigen vector, 는 eigen value를 담은 행렬
- cf) spectral decomposition
- 아래 예시에서는 변수가 m개라고 가정
- 수식은.. 손으로 쓰면서 차근차근 이해하자
- 수학적 이해는 따로 공부 필요

PCA 예제
- 위에서 언급된 알고리즘대로 차근차근 이해하면 됨
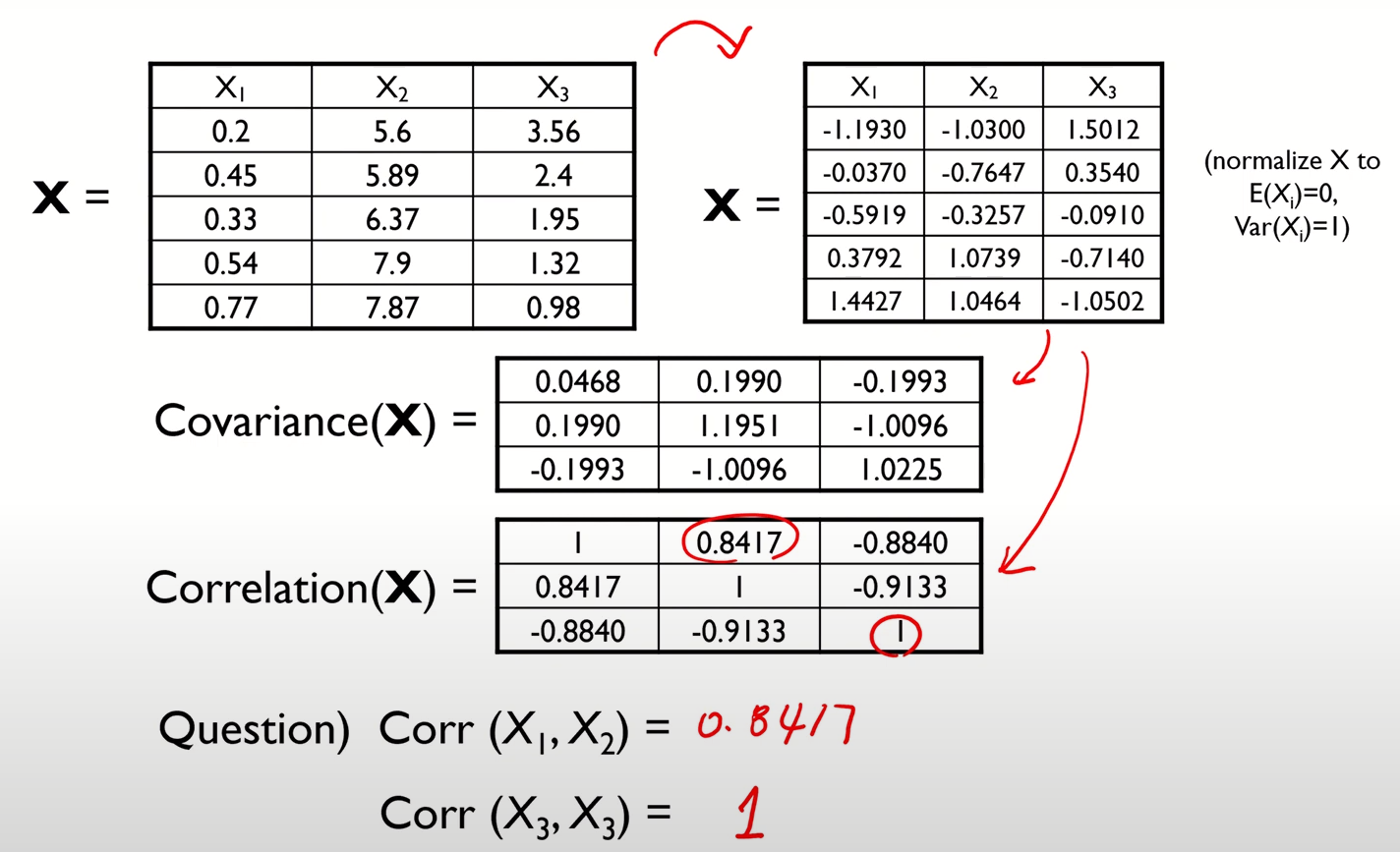

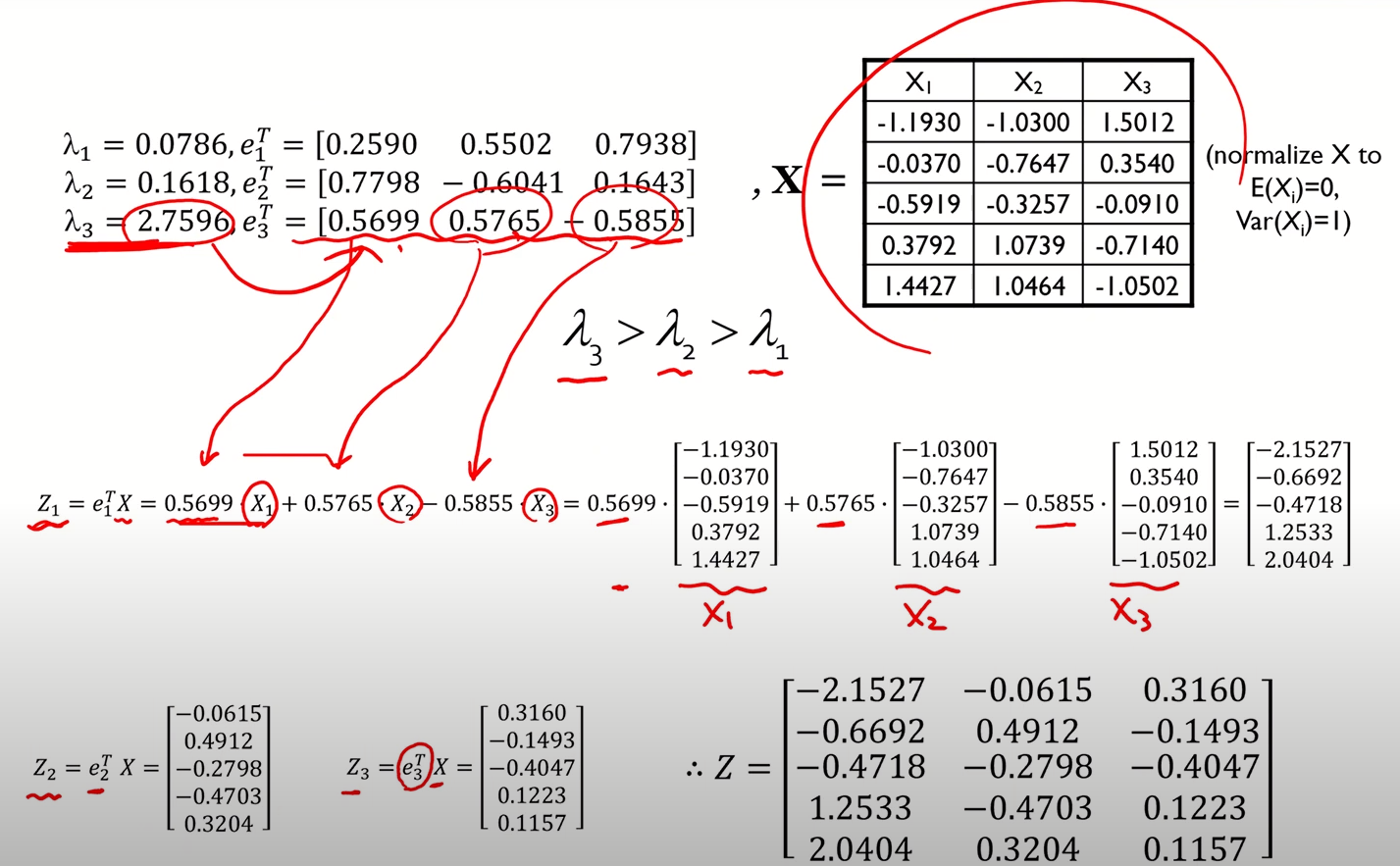


주성분 개수 선택 방안
- 차원 축소 후에도 원래 변수를 사용한 것과 최대한 유사한 효과를 내기 위해서는 몇 개의 주성분을 사용해야 하는가
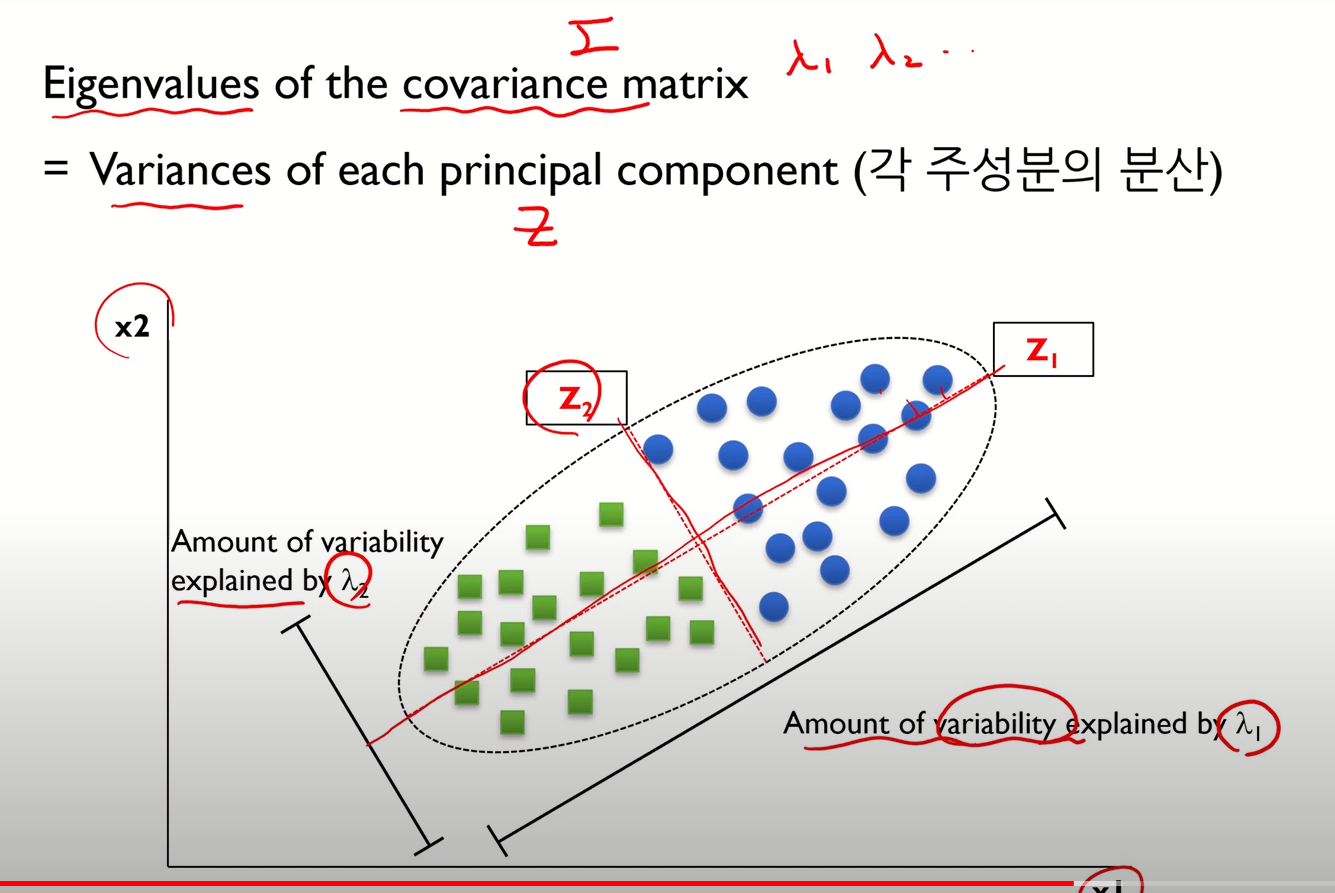
- Eigen value는 각 주성분의 분산을 의미
- 이를 이용해 주성분의 수 결정

- 위와 같이 주성분 수에 따른 원본 데이터에 대한 설명력을 구할 수 있음
- 이 예시에서는 주성분 하나만 선택해도 원본 데이터의 92%를 설명할 수 있다는 것
- 이때, 주성분 개수 선택방식 두 가지가 있다.
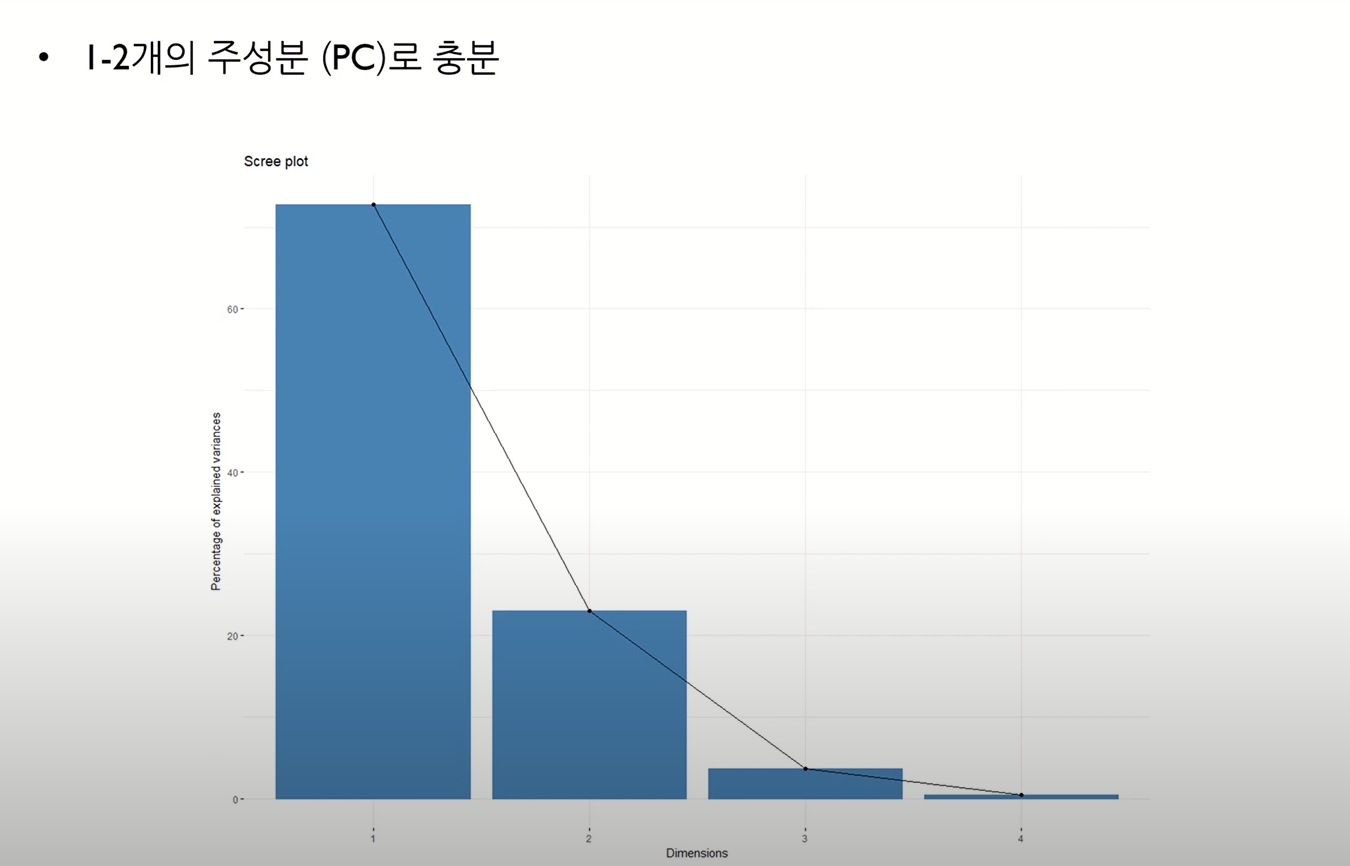
- 고유값 감소율이 유의미하게 낮아지는 Elbow Point에 해당하는 주성분 수 선택
- 일정 수준 이상의 분산비를 보존하는 최소의 주성분 선택 (보통 70% 이상)
- 물론 시각화가 목적이면 3개 이하로 해야하긴 하다만..
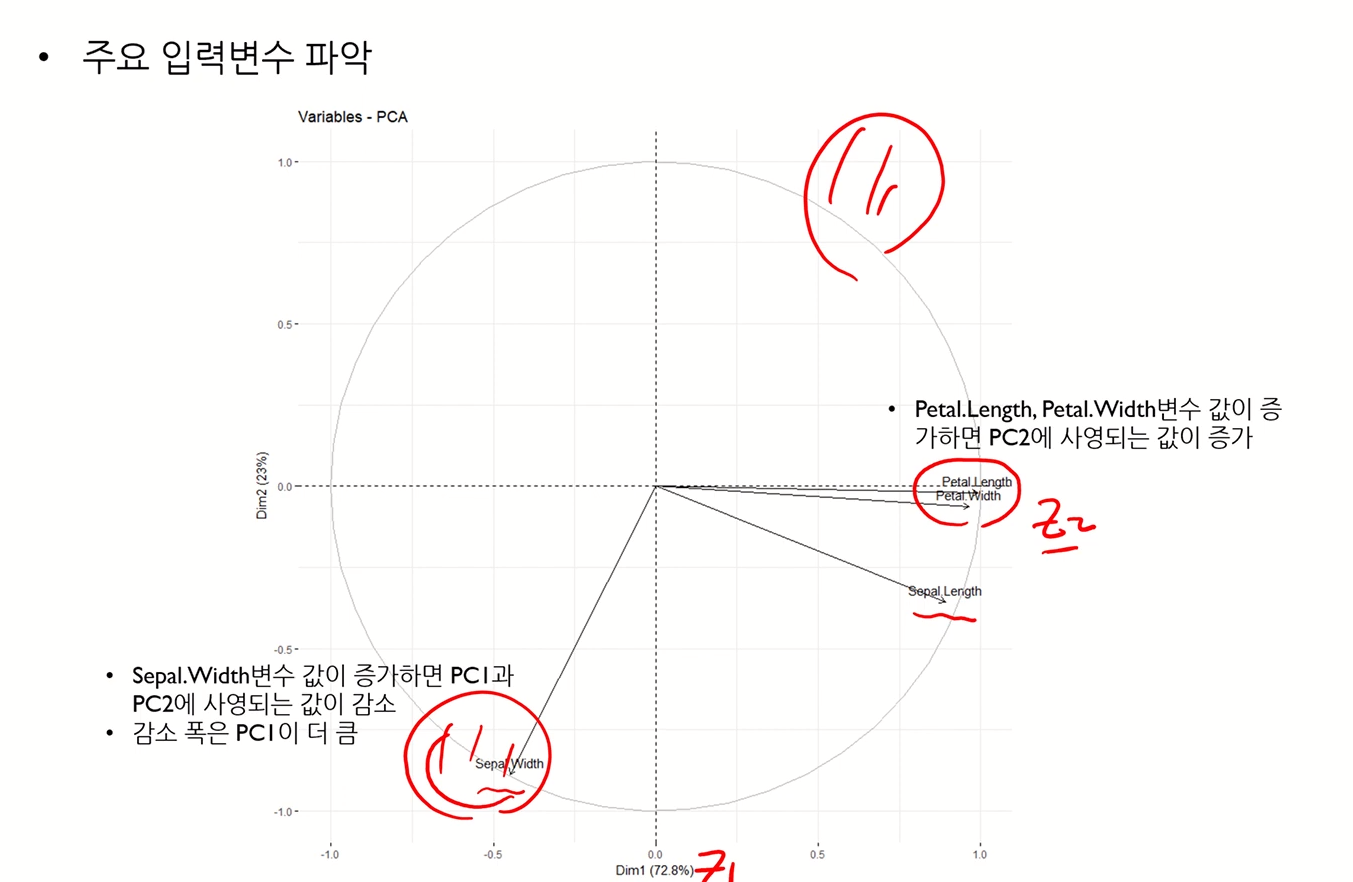
PCA Loading Plot
- 실제 변수가 주성분 결정에 얼마나 많은 영향을 끼쳤는지 알아내기 위함
- 즉, 위에서 본 주성분 추출 수식에서 계수값과 관련된 것
- 가 크다는 것은, 해당 주성분 추출에 있어 해당 변수의 영향이 크다는 것을 의미
- 즉, 위에서 본 주성분 추출 수식에서 계수값과 관련된 것
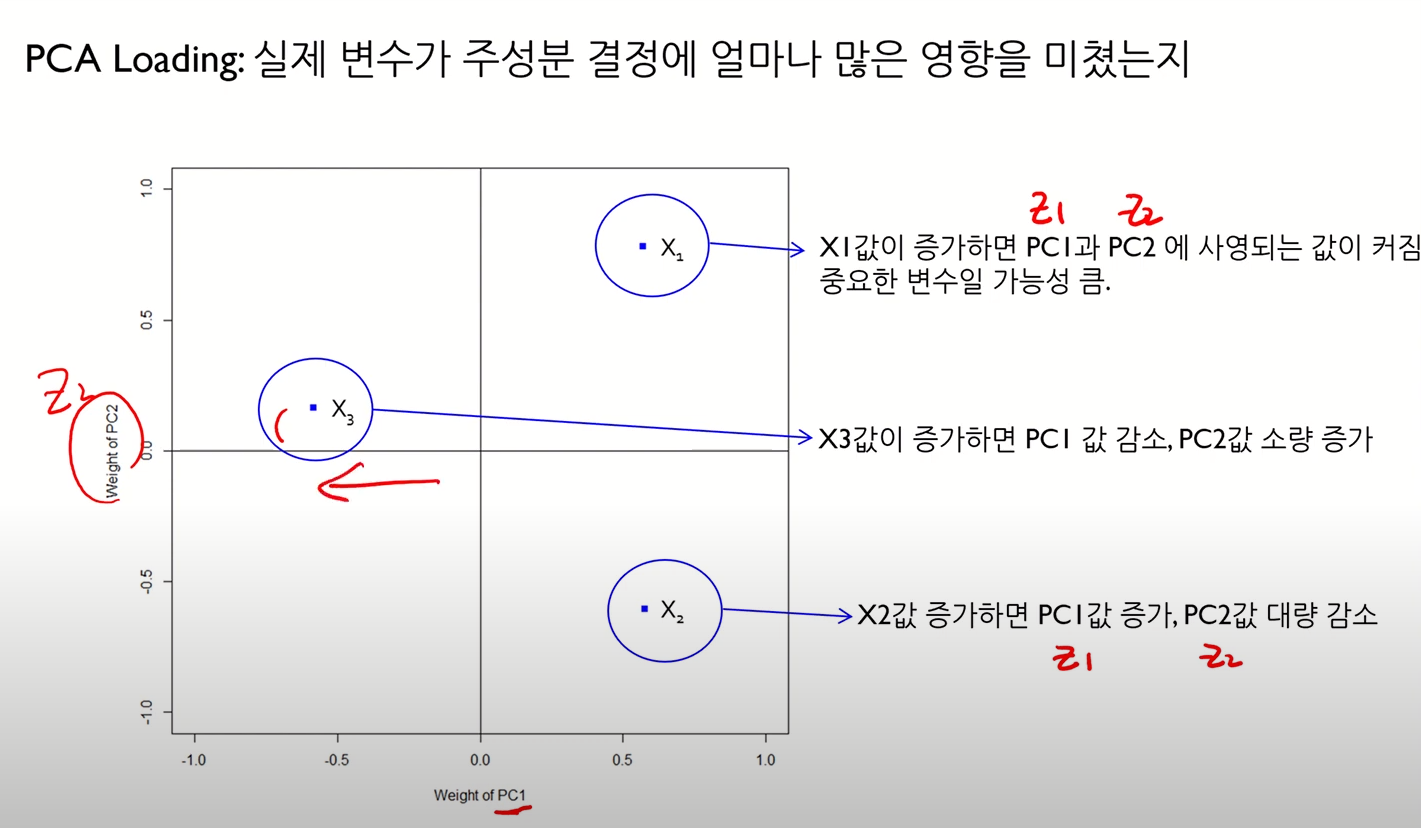
요런 느낌
PCA 알고리즘 요약
- 이때, 데이터 정규화 과정을 통해 mean centering을 한다.
- 이후 covariance matrix를 계산하는데, mean centering을 하면 covariance와 correlation이 같게 나온다.
- Mean centering과정을 거치지 않을 경우, Correlation Matrix 를 사용하는 것이 좋음
- 이후 covariance matrix를 계산하는데, mean centering을 하면 covariance와 correlation이 같게 나온다.
- 나머지 사항은 아래 슬라이드 참고

PCA 특징
- 공분산 행렬의 고유벡터를 사용하므로, 단일 가우시안(unimodal)분포로 추정할 수 있는 데이터에 대해 서로 독립적인 축을 찾는데 사용할 수 있음
PCA 한계점
한계점 1
- 데이터의 분포가 가우시안이 아니거나, 다중가우시안(multimodal) 자료들에 대해 적용이 어려움
- 이래서 지금 내가 하고있는 업무의 데이터에서 PCA의 효과를 못느꼈던 것 같다
- 결국은 PCA를 쓰지 않고 했었다.

한계점 1 대안
- 커널 PCA
- LLE (Locally Linear Embedding)
자세한 내용은 따로 공부하자
한계점 2
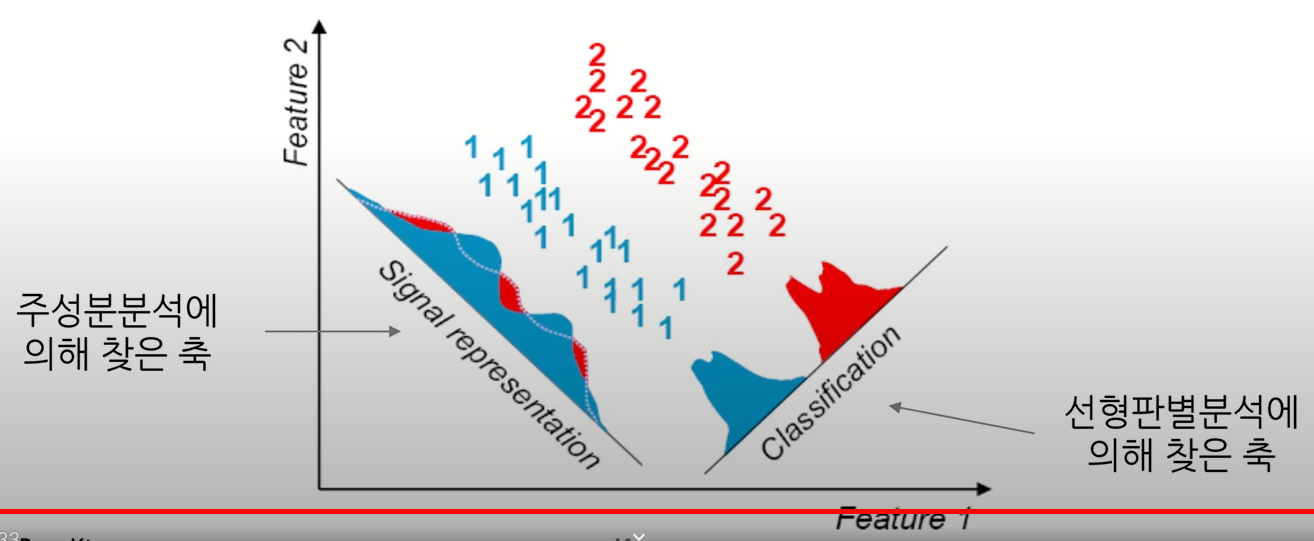
- 분류/예측 문제에 대해 데이터의 범주 정보를 고려하지 않기에, 범주간 구분이 잘 되도록 변환해주는 것은 아님
- 주성분분석은 단순히 변환된 축이 최대 분산방향과 정렬되도록 좌표회전을 수행하는 것이기 때문
- Unsupervised Feature Extraction
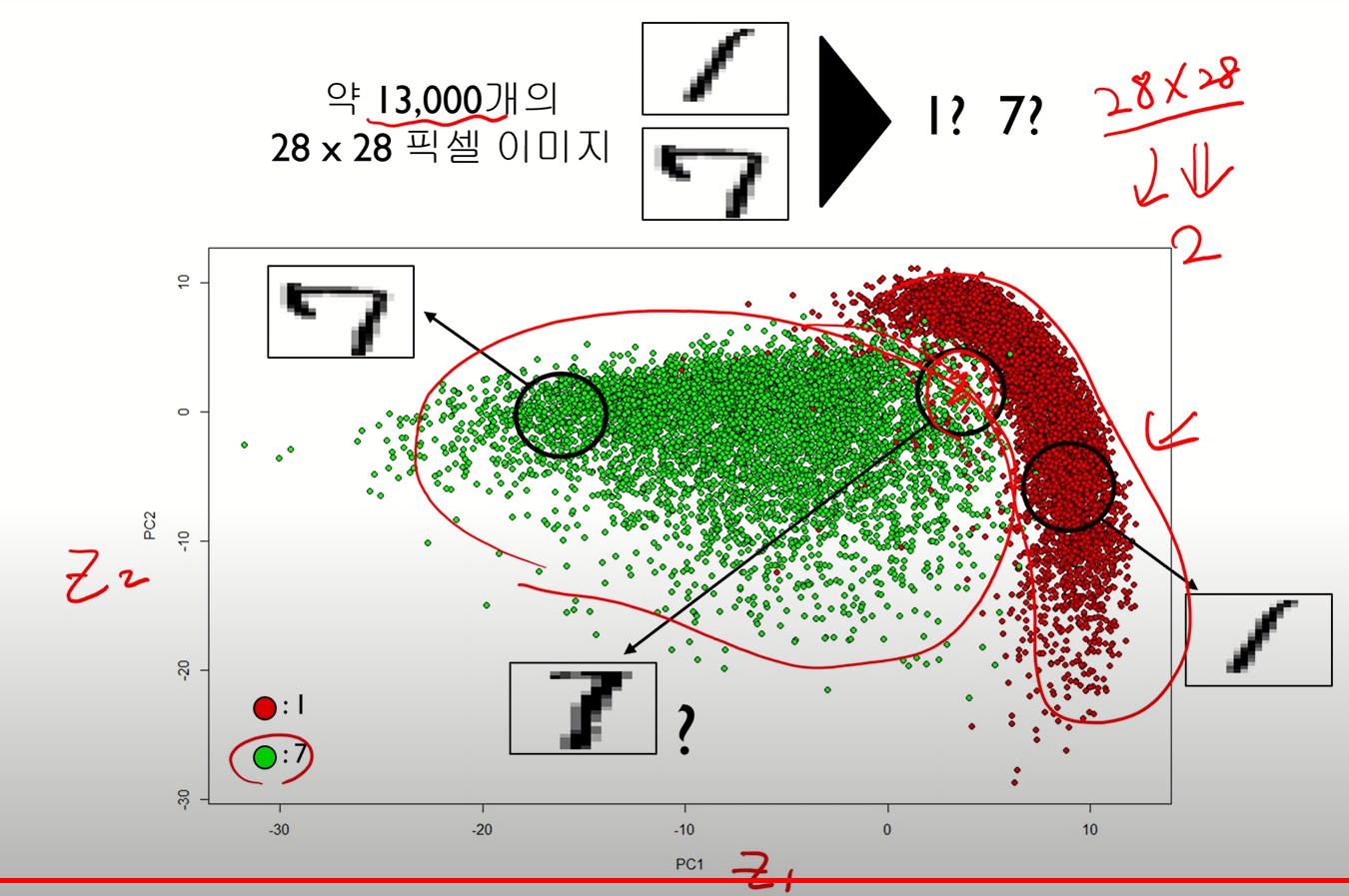
- 주성분분석은 단순히 변환된 축이 최대 분산방향과 정렬되도록 좌표회전을 수행하는 것이기 때문
한계점 2 대안
- Partial Least Square (PLS)
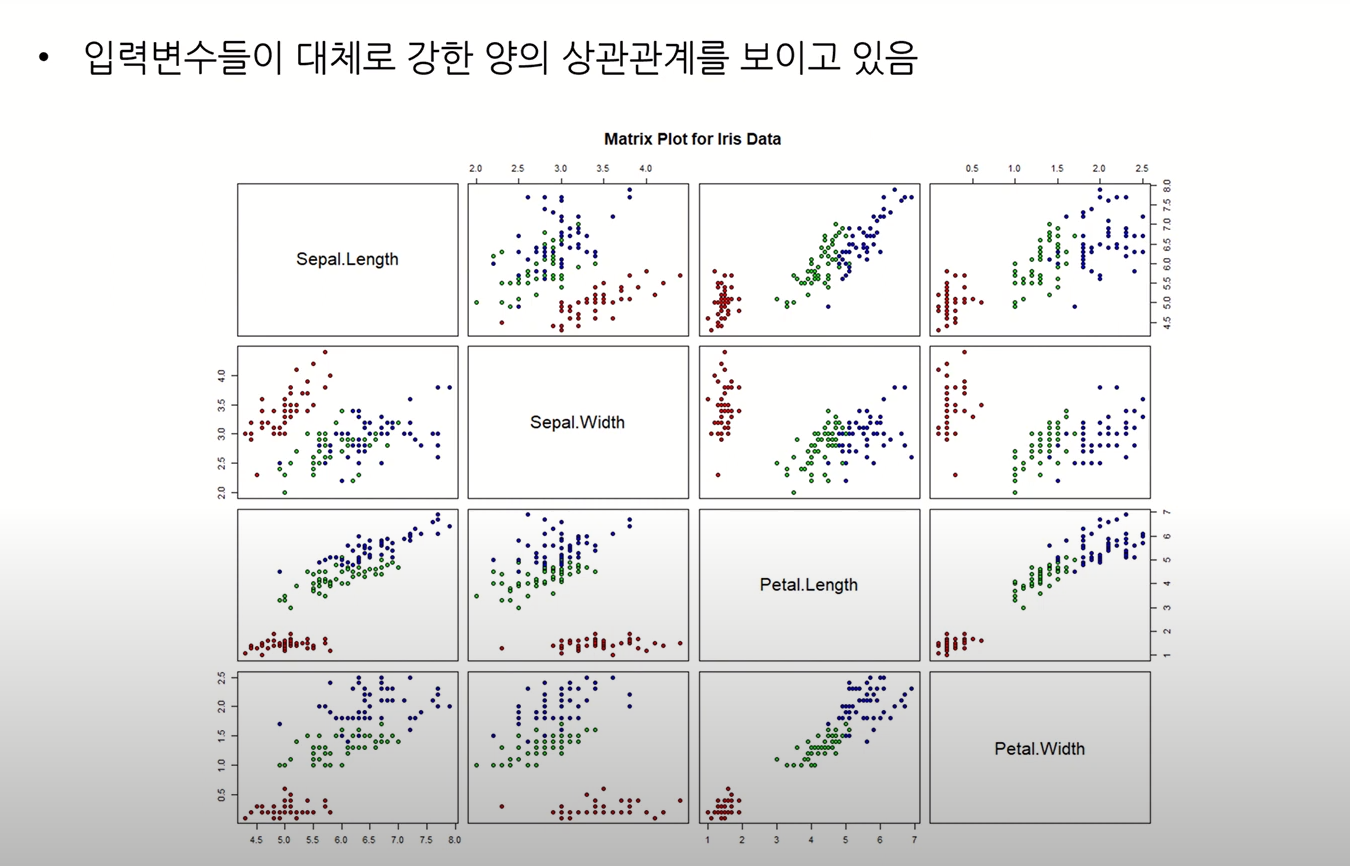
IRIS 데이터 사용한 PCA 예시