https://www.youtube.com/watch?v=8zB-_LrAraw&list=LL&index=1&t=5s
위 자료를 참고했다.
군집화란?
군집화 기준
- 군집 내 유사도는 최대화될수록, 군집 간 유사도는 최소화될수록 좋음
적용사례
- 고객 클러스터링 -> 내가 하고 있는 것
- 유사 문서 군집화
- 웨이퍼 Fail bit map 군집화 -> 웨이퍼 불량 패턴 확인 가능
등등..
주요 고려사항
유사도 측정 기준으로 어떤 거리 척도를 사용할 것인가
Euclidean Distance = L2 norm
Manhattan Distance = L1 norm
Mahalanobis Distance
-
변수 내 분산 & 변수 간 공분산을 모두 반영해 X, Y 간 거리를 계산
-
데이터의 covariance matrix가 identity matrix인 경우, Euclidean distance와 동일
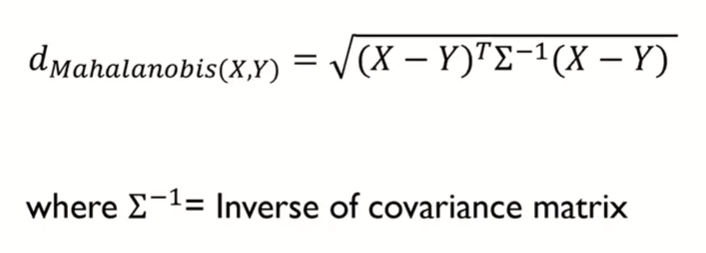
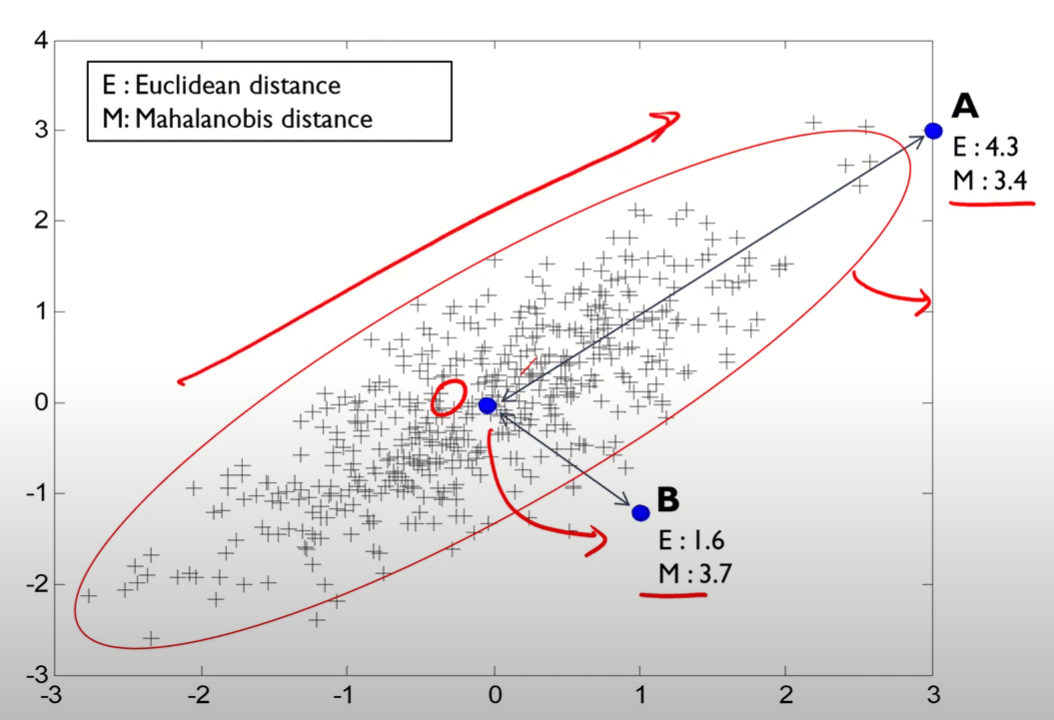
마할라노비스 거리를 기준으로 했을 때, A보다 B와의 거리가 더 먼 것을 알 수 있다.
Correlation Distance
-
상관계수는 -1~1 사이의 값을 가짐
-
즉, Correlation Distance는 0~2 사이의 값을 갖게 됨
-
상관계수 거리 관점에서 봤을 떄, 1번 그림에 대해서는 상관계수 거리가 크지 않을 것이다.
- 패턴이 유사하기 때문!
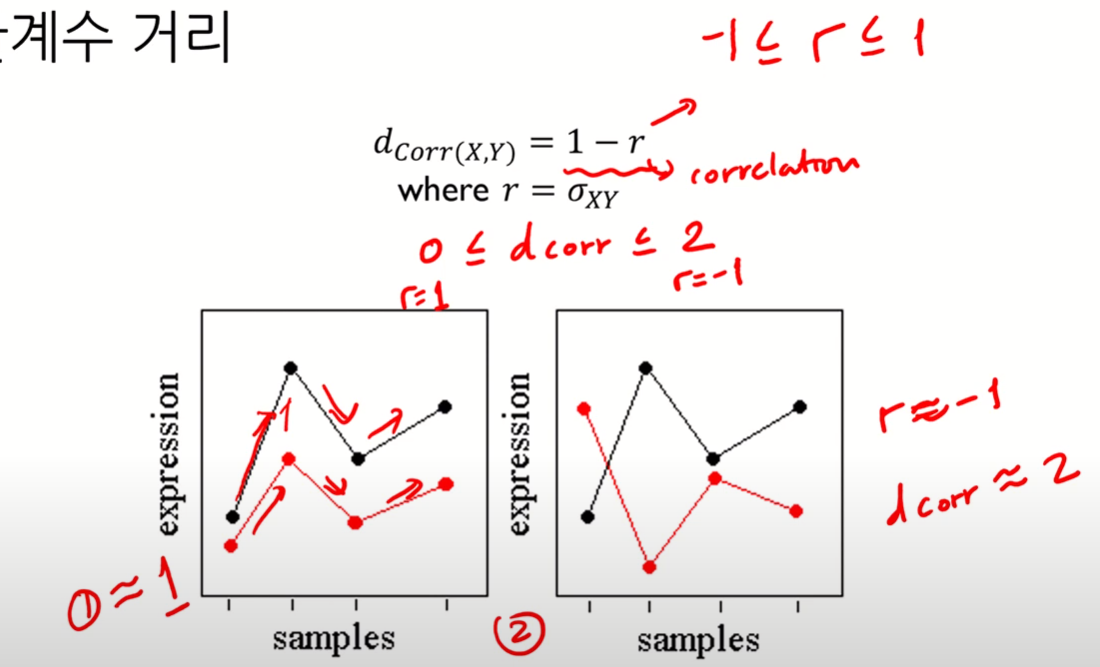
- 패턴이 유사하기 때문!
-
Correlation distance는 데이터 간 Pearson correlation을 거리 척도로 직접 사용하는 방식으로, 데이터 패턴의 유사도/비유사도를 반영할 수 있다.
Spearman Correlation Distance
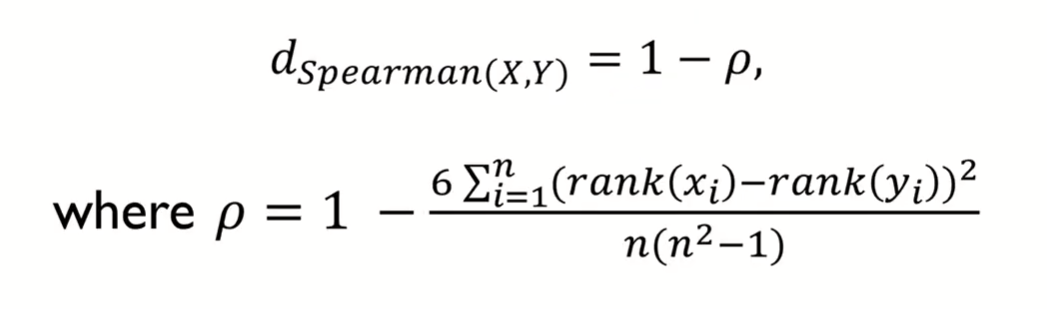
- 어기서 는 Spearman correlation으로, 데이터의 rank를 이용해 Correlation distance를 계산하는 방식이다.
- 의 범위는 -1~1로, Pearson Correlation과 동일하다.
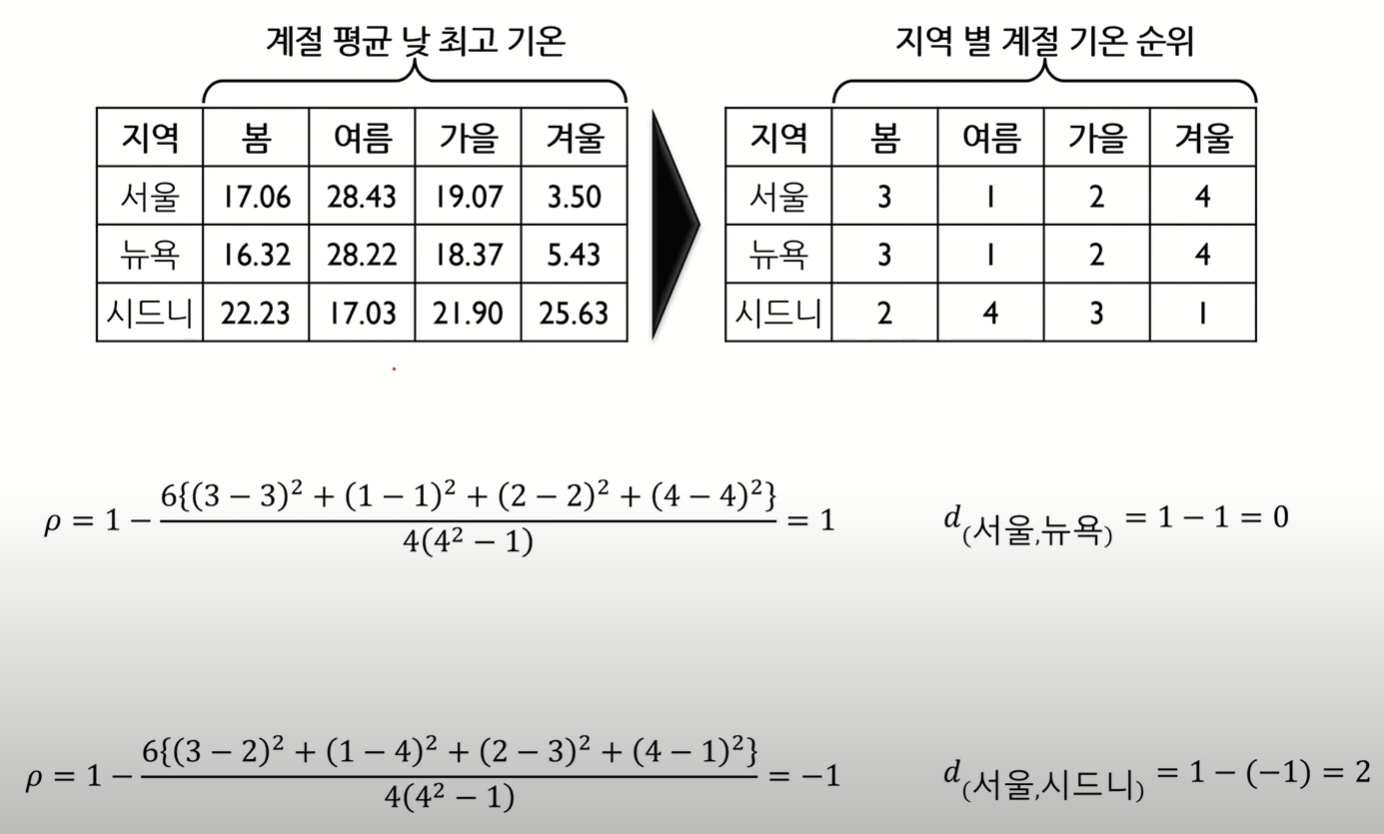
어떤 군집화 알고리즘을 선택할 것인가
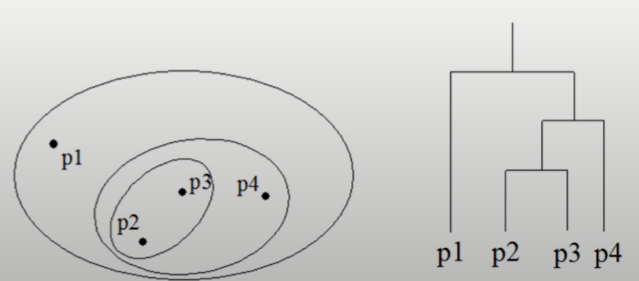
계층적 군집화
- 개체들을 가까운 집단부터 차근차근 묶어나가는 방식
- 군집화 결과 뿐 아니라, 유사한 개체들이 결합되는 dendrogram 생성
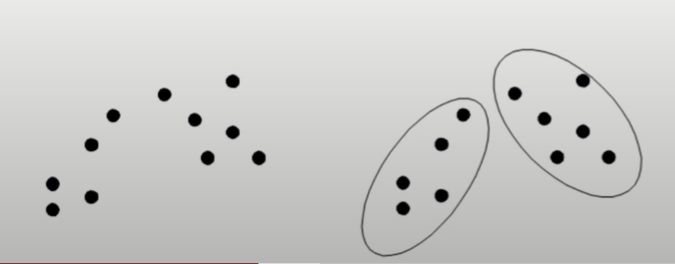
분리형 군집화
- 전체 데이터의 영역을 특정 기준에 의해 동시에 구분
- 각 개체들은 사전에 정의된 개수의 군집 중 하나에 속하게 됨
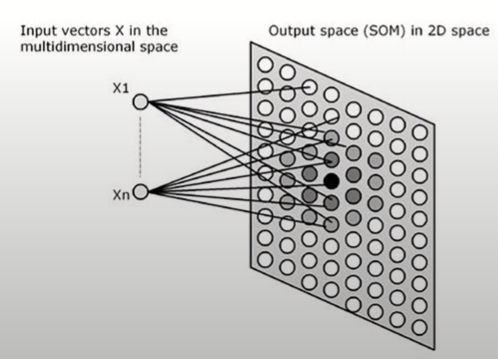
자기조직화지도
- 2차원의 격자에 각 개체들이 대응하도록 인공신경망과 유사한 학습을 통해 군집 도출
분포 기반 군집화
- 데이터의 분포를 기반으로 높은 밀도를 갖는 세부 영역들로 전체 영역을 구분
최적 군집 수를 어떻게 결정할 것인가
- 다양한 군집 수에 대해 성능 평가 지표를 도시하여 최적의 군집 수 선택 (Elbow method)
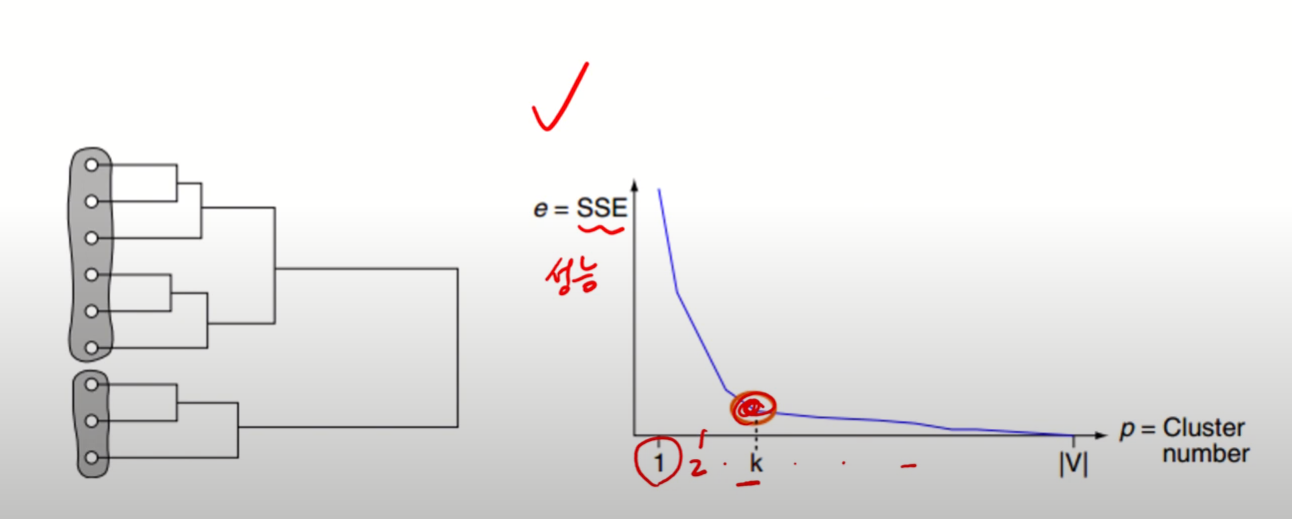
군집화 결과를 어떻게 측정/평가할 것인가
SSE (Sum of Squared Error)
- 군집 내 거리는 잘 계산하지만, 군집 간 거리는 고려하지 못하는 문제 존재
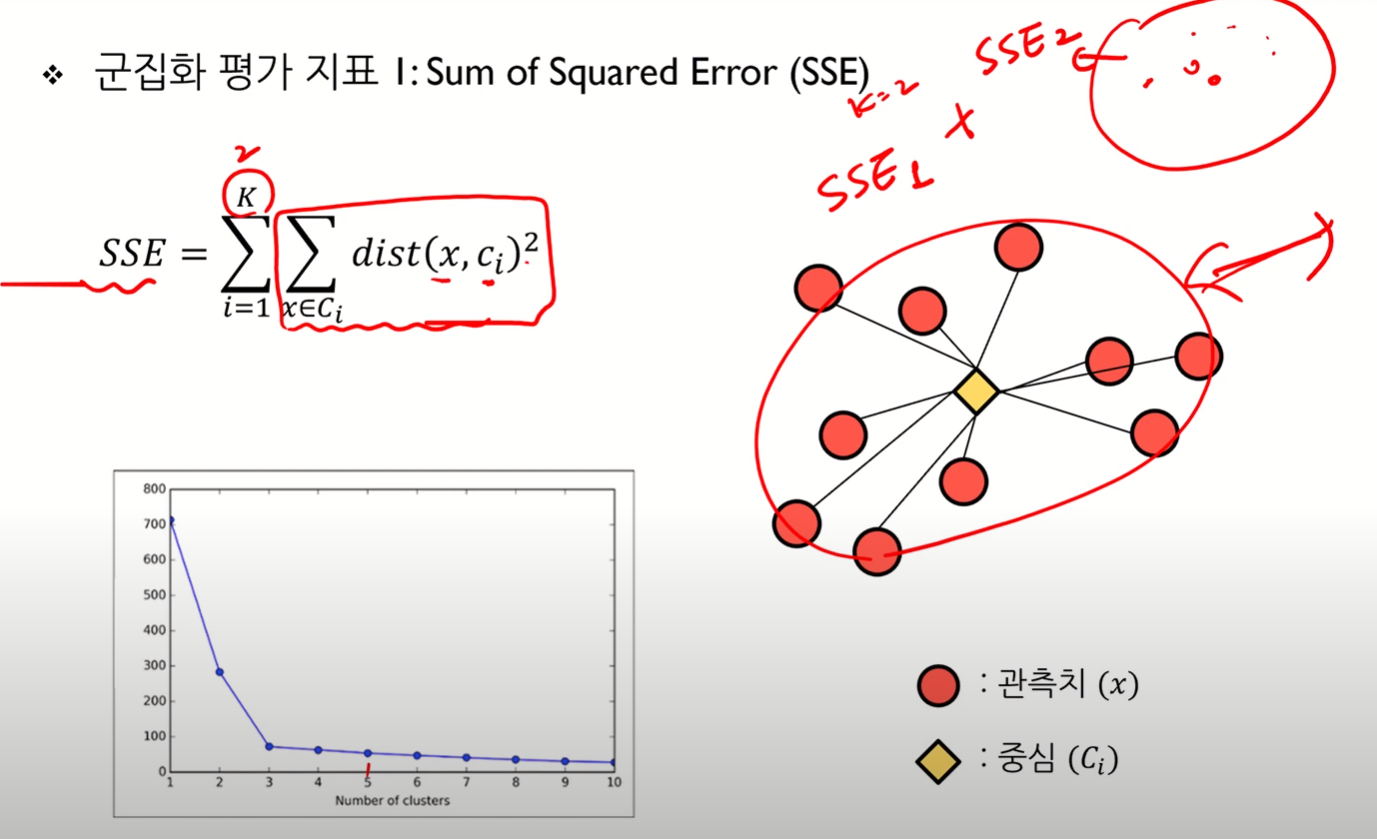
Silhouette 통계량
- 군집 내 거리 / 군집 간 거리를 모두 고려 가능
- 실루엣 계수는 관측치 개수만큼 나온다!
- 대표값은 각 관측치 당 실루엣 계수의 평균으로 한다.
- 즉, 계수가 클 수록 군집이 잘 되었다는 것
- 수식에서 분모 부분은 scaling의 역할을 함
- 수식에서 a(i)는 작을 수록, b(i)는 클 수록 좋음
- 일반적으로 실루엣 통계량 대표값이 0.5보다 크면 군집 결과가 타당하다 보며, -1에 가까우면 군집이 전혀 되지 않았다는 것을 의미한다.
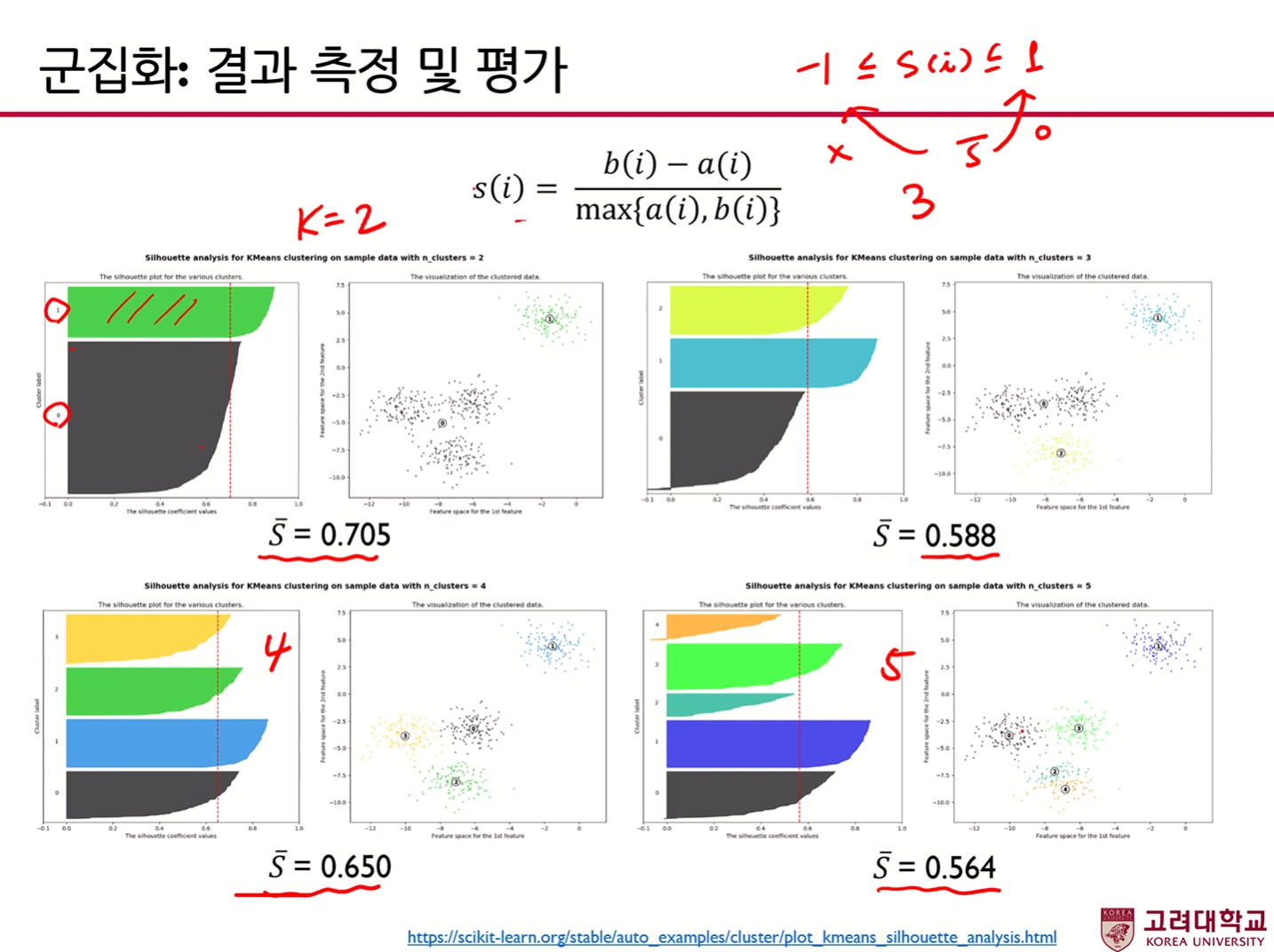
위 결과를 보면 K=2일때 실루엣계수가 가장 높으나, 보통 K=2일때 실루엣 계수가 가장 높은 경향이 있으므로, Second best를 K 개수로 삼는 경우가 많다고 한다.
계층적 클러스터링 심화
계층적 군집화 (Hierarchical Clustering)
- 계층적 트리모형 이용해 개별 개체들을 순차적/계층적으로 유사한 개체/군집과 통합
- 덴드로그램(Dendrogram)을 통해 시각화 가능
- 사전에 군집 수를 정하지 않아도 수행이 가능하다!
- 덴드로그램 생성 후 적절한 수준에서 자르면 그에 해당하는 군집화 결과 생성
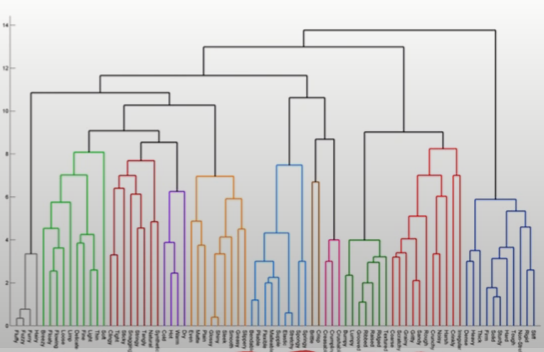
- 덴드로그램 생성 후 적절한 수준에서 자르면 그에 해당하는 군집화 결과 생성
단계
-
모든 개체들 사이의 거리에 대한 유사도 행렬 계산
-
거리가 인접한 관측치끼리 군집 형성
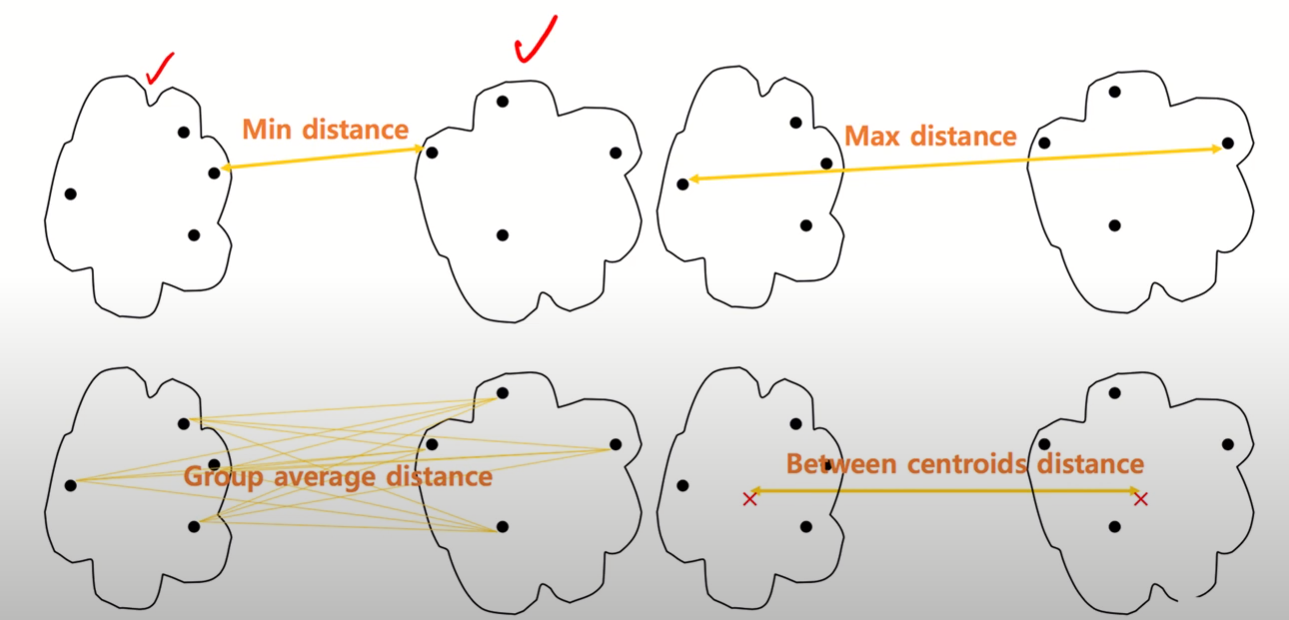
- 이때, 군집 간 거리 측정 방법
- 관측치 간 거리 중 최소값, 최대값, 평균 등..의 값 사용 가능
- User가 결정!
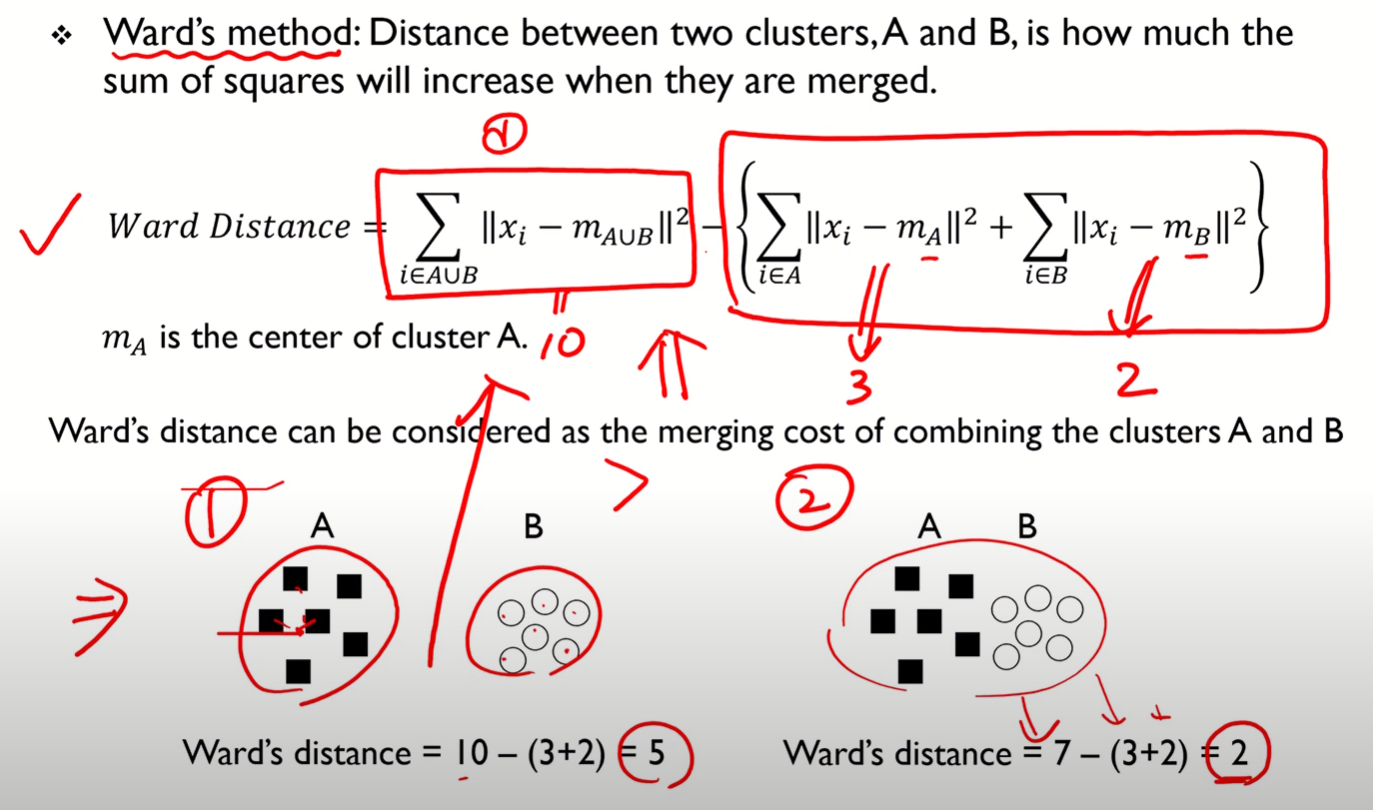
- Ward method
- 굉장히 많이 쓰이며, 계층적클러스터링에서 좋은 결과를 내는 경향을 보임!
- 수식을 보고 잘 이해하도록 하자.
- 이때, 군집 간 거리 측정 방법
-
유사도 행렬 업데이트
-
반복..
K-평균 군집화 (K-Means Clustering)
- 대표적 분리형 군집화 알고리즘
- 각 군집은 하나의 중심 (centroid)을 가짐
- 각 개체는 가장 가까운 중심에 할당되며, 같은 중심에 할당된 개체들이 모여 하나의 군집 형성
- 하나의 군집 수 K가 정해져야 알고리즘 실행 가능
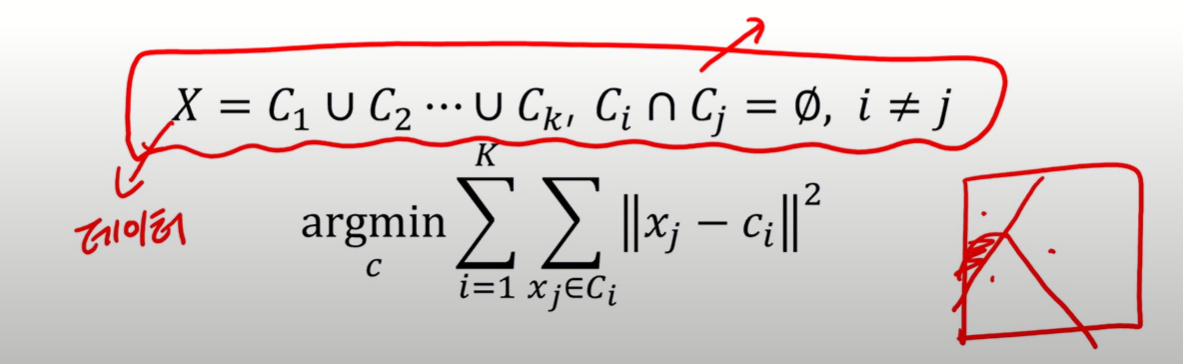
단계
- k개의 중심을 임의로 생성
- 생성된 중심을 기주능로 모든 관측치에 군집 할당
- 각 군집의 중심 다시 계산
- 중심이 변하지 않을 때까지 2~3번 단계 반복
문제점
-
초기 중심 설정이 최종 결과에 영향을 준다!
- 해당 문제 해결 방안
- 반복적으로 수행해 가장 여러 번 나타나는 군집 사용
- 전체 데이터 중 일부만 샘플링해 계층적군집화 수행한 뒤 쵝군집 중심 설정
- 데이터 분포의 정보 사용해 초기 중심 설정
- 그러나 많은 경우엔 초기 중심 설정이 최종 결과에 큰 영향을 미치지는 않는다고 한다. (매우 민감하진 않음)
- 해당 문제 해결 방안
-
서로 다른 크기의 군집을 잘 찾아내지 못한다
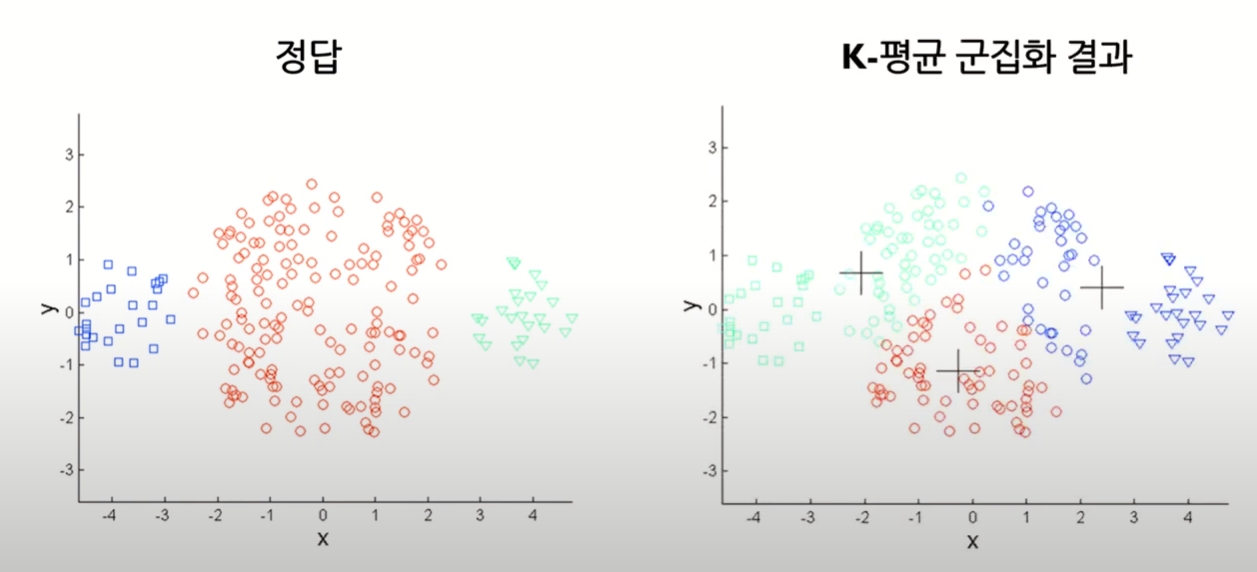
-
서로 다른 밀도의 군집을 잘 찾아내지 못한다
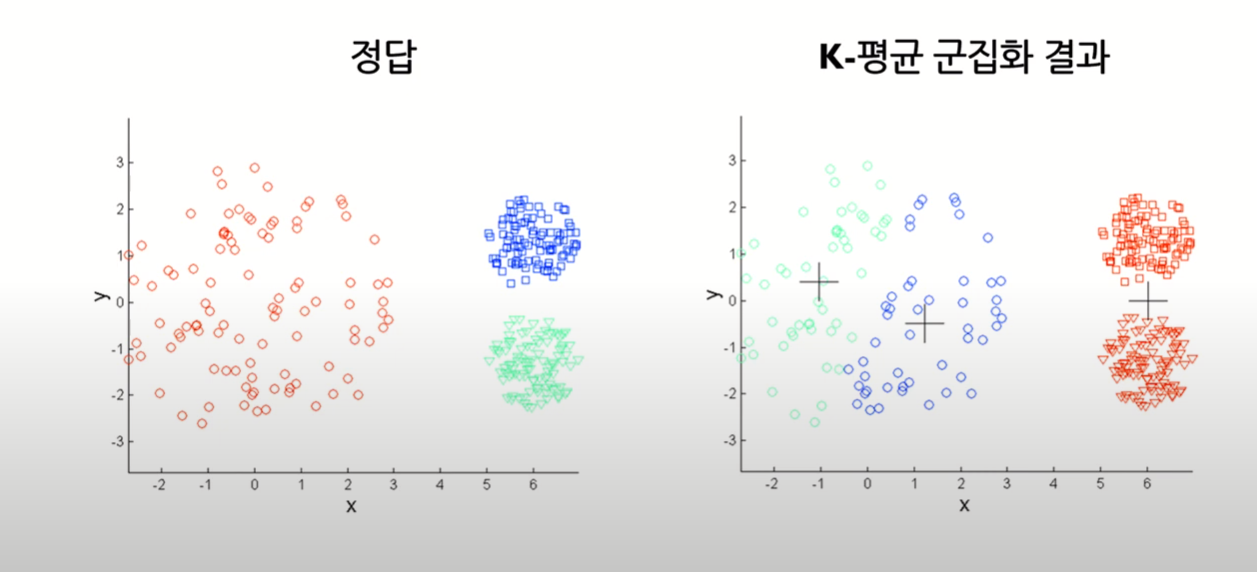
-
지역적 패턴이 존재하는 군집을 판별하기 어렵다
- 아래 그림은 거리 metric으로 Euclidean distance를 사용했을 때의 결과다.
- 지역적 패턴이 존재하는 경우 사용할 수 있는 distance metric으로는 Geodesic distance이 있다!
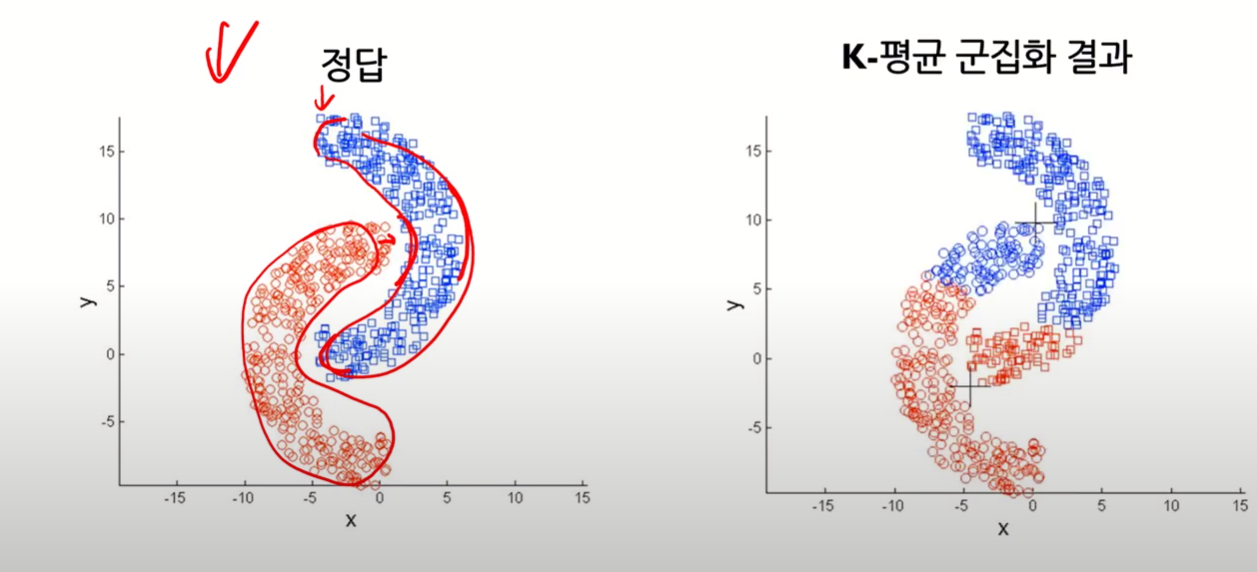
문제 해결 방안
- 여러 번 수행한 뒤, 다수로 나온 결과를 사용하거나,
- 계층적 클러스터링을 통해 중심점을 설정한다.
- 이러한 단점들에도 불구하고, 여전히 많이 쓰이는 알고리즘!
여담
- 뭐든 어떤 방법론을 적용하기 이전, 해당 방법론에 대해 잘 이해하도록 하자.
마음이 급해서 변수 뽑고 모델 적용을 하다 보니 비효율적으로 업무를 하게 되는 것 같았는데, 오늘 알게된 개념으로 내일부터 다시 차근차근 적용해보자!
