https://www.youtube.com/watch?v=GbCAwVVKaHY
https://huidea.tistory.com/296
위 자료를 참고했다.

---

오랜만의 기록~
필기를 기반으로 작성하는 거라 깔끔하지 않을 수 있다

---

VAE 구조

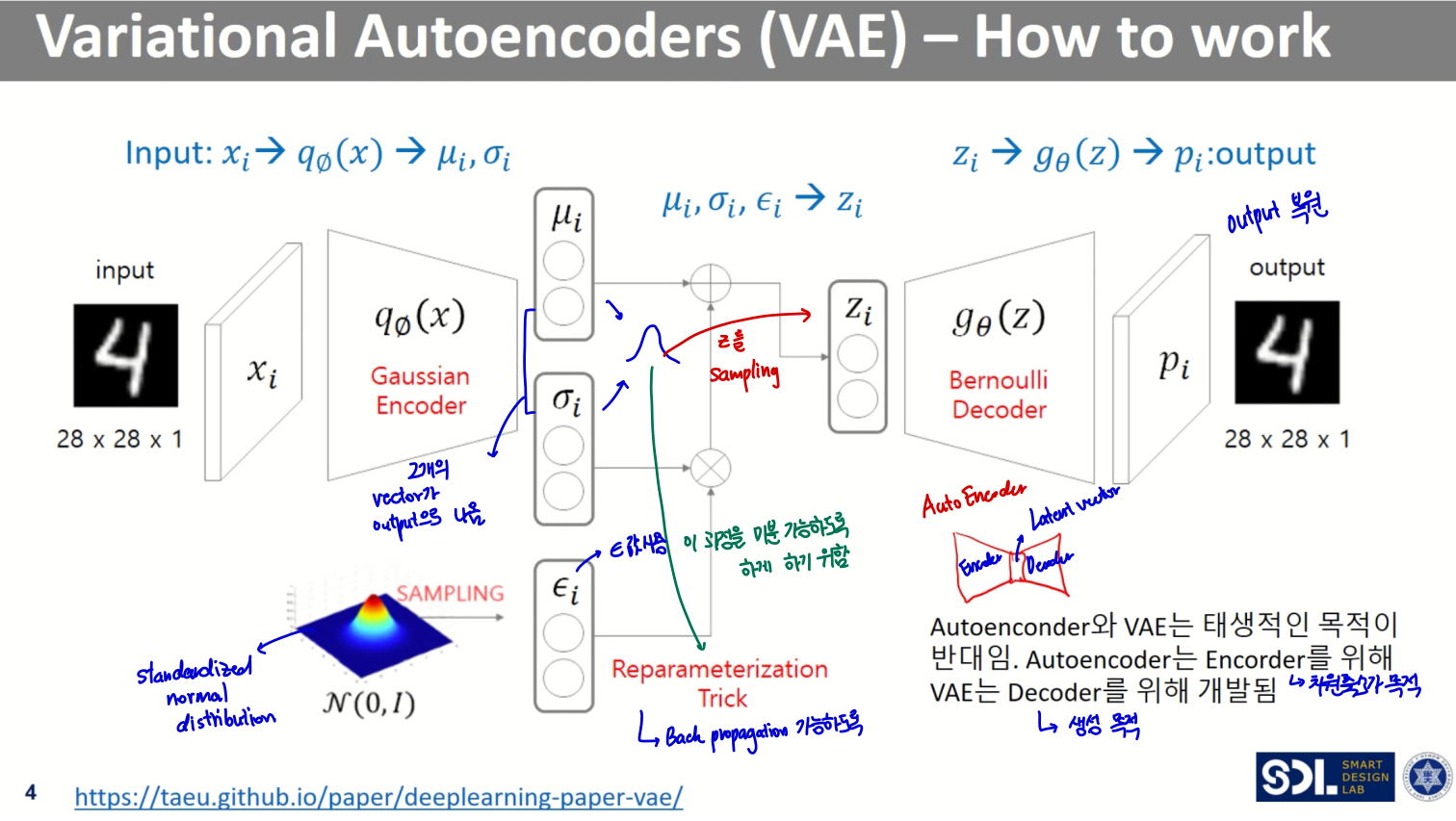
전체 모델 구조는 위와 같다.

AutoEncoder를 기반으로 하지만, 태생적인 목적이 다르다.

• AutoEncoder는 $z$를 잘 임베딩하는 것(차원축소)이 목적인 반면,
• VAE는 원본데이터를 기반으로 원본과 비슷한 데이터를 생성해내는 것이 목적이다

Encoder (Gaussian)

• n차원의 벡터 두 개(평균, 표준편차)를 반환한다
  • n차원의 평균, 표준편차 두 벡터를 기반으로 n개의 분포로부터 n차원의 $z$를 샘플링해내는 것
    • ...을 목표로 했으나, 그 과정은 미분이 불가능하므로 Backpropagation이 불가하다
    • 이를해결하기 위해 Reparameterization Trick을 적용한다.

Reparameterization Trick

• 표준정규분포로부터 샘플링해낸 $\epsilon$를 표준편차에 곱해주고, 평균을 더해준다
  • $\mu$+$(\epsilon*\sigma)$

Decoder (Bernoulli)

• n차원의 $z$를 입력으로 받아 원본과 '비슷한' 데이터를 생성해낸다

---

Loss function

• VAE의 loss function은 크게 두 부분으로 구성된다

  • Reconstruction Error
    • output의 분포 가정에 따라 수식이 다르다
      • 분포 가정이 normal distribution인 경우, MSE
      • 분포 가정이 Bernoulli distribution인 경우, Cross Entropy

  상세 수식은 아래에서!

  • Regularization
    

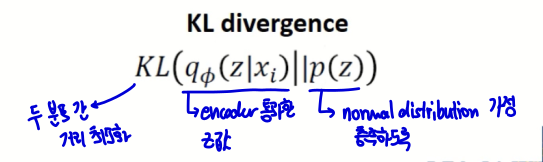
    • $p(z)$는 표준정규분포를 따른다는 가정 존재
    • encoder를 통과한 후의 $z$는 정규분포를 따른다
    • encoder를 통과한 후의 $z$값과 $p(z)$ 두 분포 간 거리를 최소화하자
      • KL Divergence 사용

Loss function 상세

• input $x$가 나올 확률이 최대화되는 distribution을 찾는 것이 목표
  상세 수식은 아래와 같다. (베이즈 정리 참고)
  
  그러나, 이를 계산하기 어려운 것이 문제
  모든 $z$에 대해 계산하기 어렵다

게다가 Posterior density 또한 구하기 어렵다

따라서, $p_\theta(x|z)$를 모델링하기 위해 $p_\theta(z|x)$를 근사하기 위한 encoder network $q_\phi(z|x)$를 정의한다.

• 디코더 학습을 위해 인코더의 도움을 받는 것

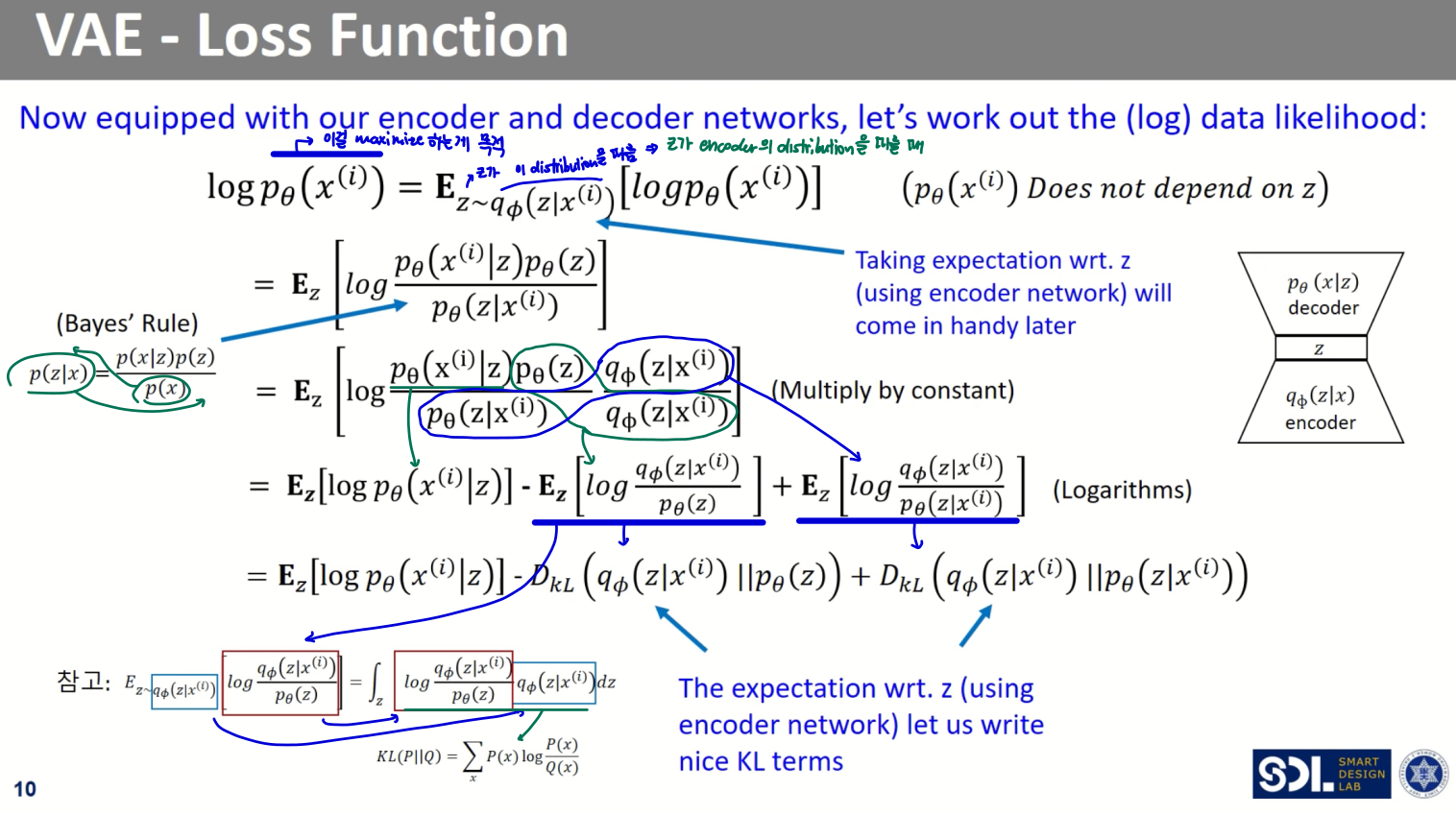
그 과정에 대한 수식을 자세히 보면 위와 같다.
또, 위 식을 다시 정리해보면 아래와 같다.

이때, 위에서 봤듯이 마지막 항에 대한 계산값은 구할 수 없다.
하지만, KL Divergence의 계산값은 항상 0보다 크다!

결국 앞의 두 항에 대한 값을 최대화하면 되는 것이다.

• 이 두 항의 값을 lower bound값으로 간주하는 것. 이 lower bound 값을 최대화하자

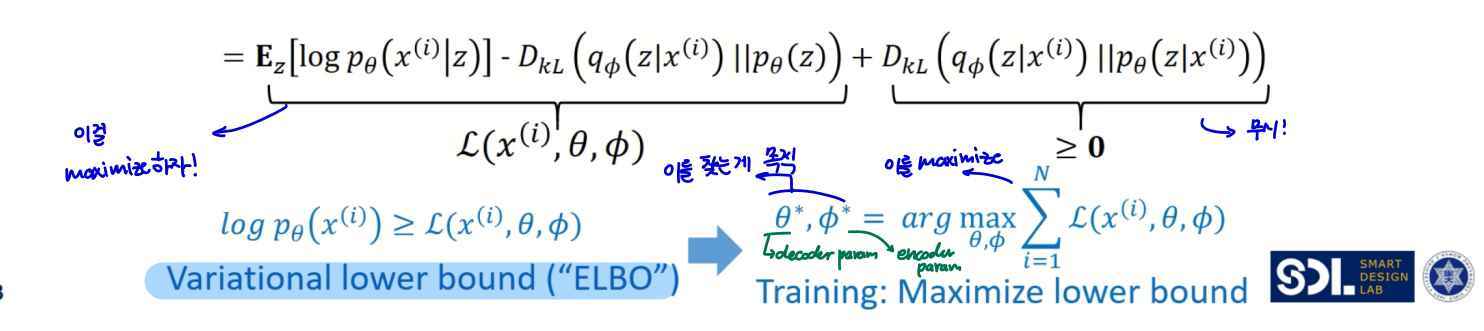
이 lower bound 값을 Variational lower bound라 하고, 줄여 ELBO라고 한다.

• 이 ELBO값을 최대화하는 decoder, encoder parameter를 찾는 것이 목적!

앞에서 구한 식을 다시 정리하면 위처럼 된다.
일반적으로, Loss가 최소화되도록 학습시키므로, 각 항에 -를 적용해준다.
그 식을 두 부분으로 나누면 Reconstruction Error와 Regularization항이 되는 것

Regularization 상세

• 샘플링의 용의성과 생성 데이터에 대한 통제성을 위한 조건을 prior에 부여하고, 이와 유사해야한다는 조건을 부여해준다.
• $x$가 주어졌을 때 $z$의 distribution이 가정한 $z$의 distribution과 일치하도록 하는 것!

즉, 아래 두 가정이 존재한다.

• encoder 통과 결과는 diagonal covariance를 갖는 multivariate gaussian distribution을 따른다
• 그런데, 이 z에 대한 prior $p(z)$는 multivariate normal distribution을 따른다고 가정한다.

위 가정에 따라 수식을 다시 전개해보면,

위와 같이 되고, 인코더를 통과한 평균, 표준편차 벡터를 통해 최종 수식값에 대한 결과(Regularization term값)를 계산할 수 있게 된다

Reconstruction Error 상세

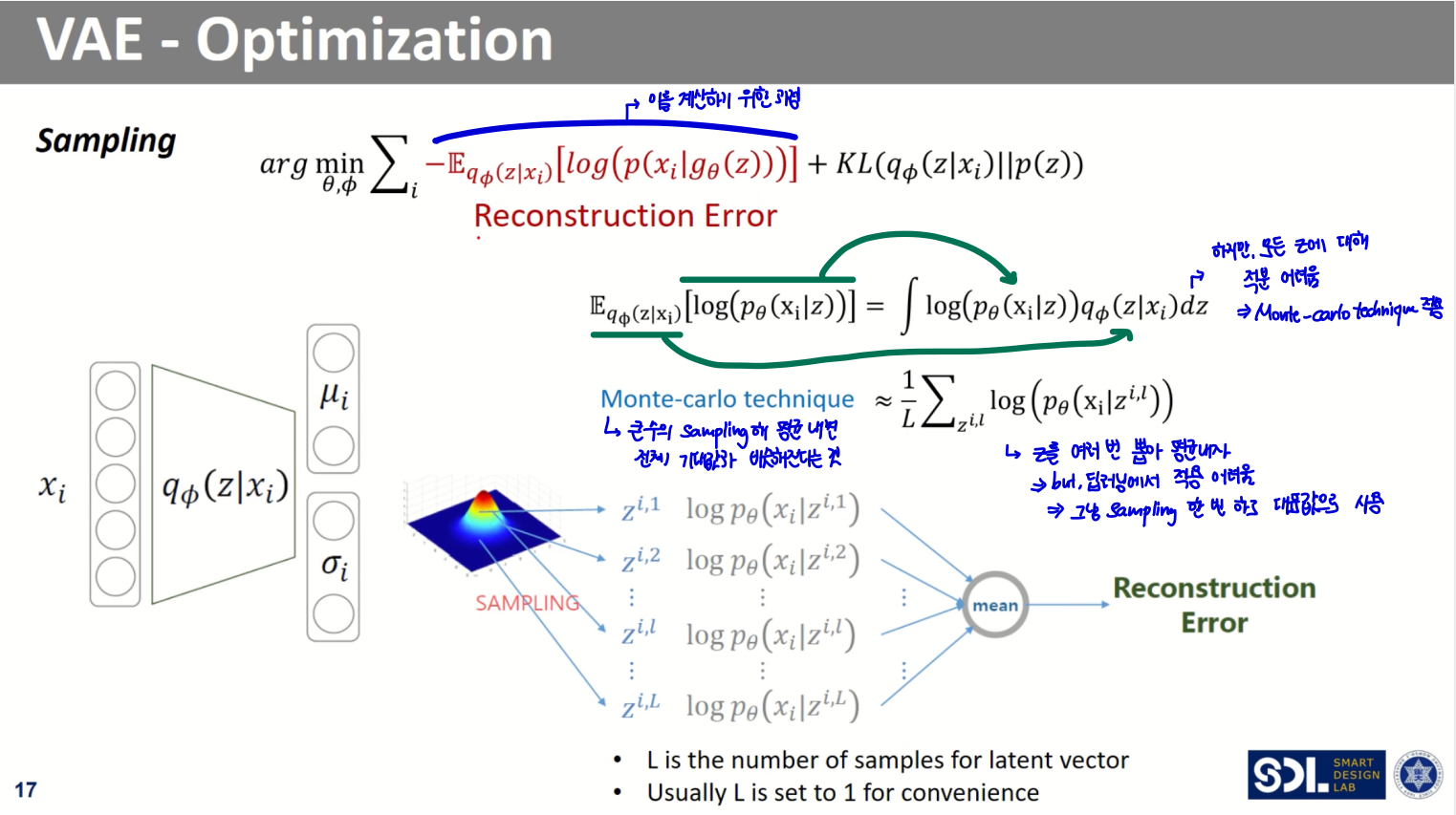
Reconstruction error 계산의 경우, 앞서 언급했다시피 모든 $z$에 대해 적분하기 어렵다는 문제가 있다.

• 이를 해결하기 위해 Monte-carlo technique을 적용해준다.
  • 그러기 위해서는 $z$를 여러 번 뽑아 평균해야 하나, 딥러닝에서 적용하긴 어렵다
  • 그냥 sampling 한 번 해서 그걸 대표값으로 사용하자!
    • 그러나, 이러한 sampling 과정은 미분 불가능 -> Backprop 불가
    • 이를 해결하기 위해 Reparameterization trick을 적용해준다

Reparameterization Trick

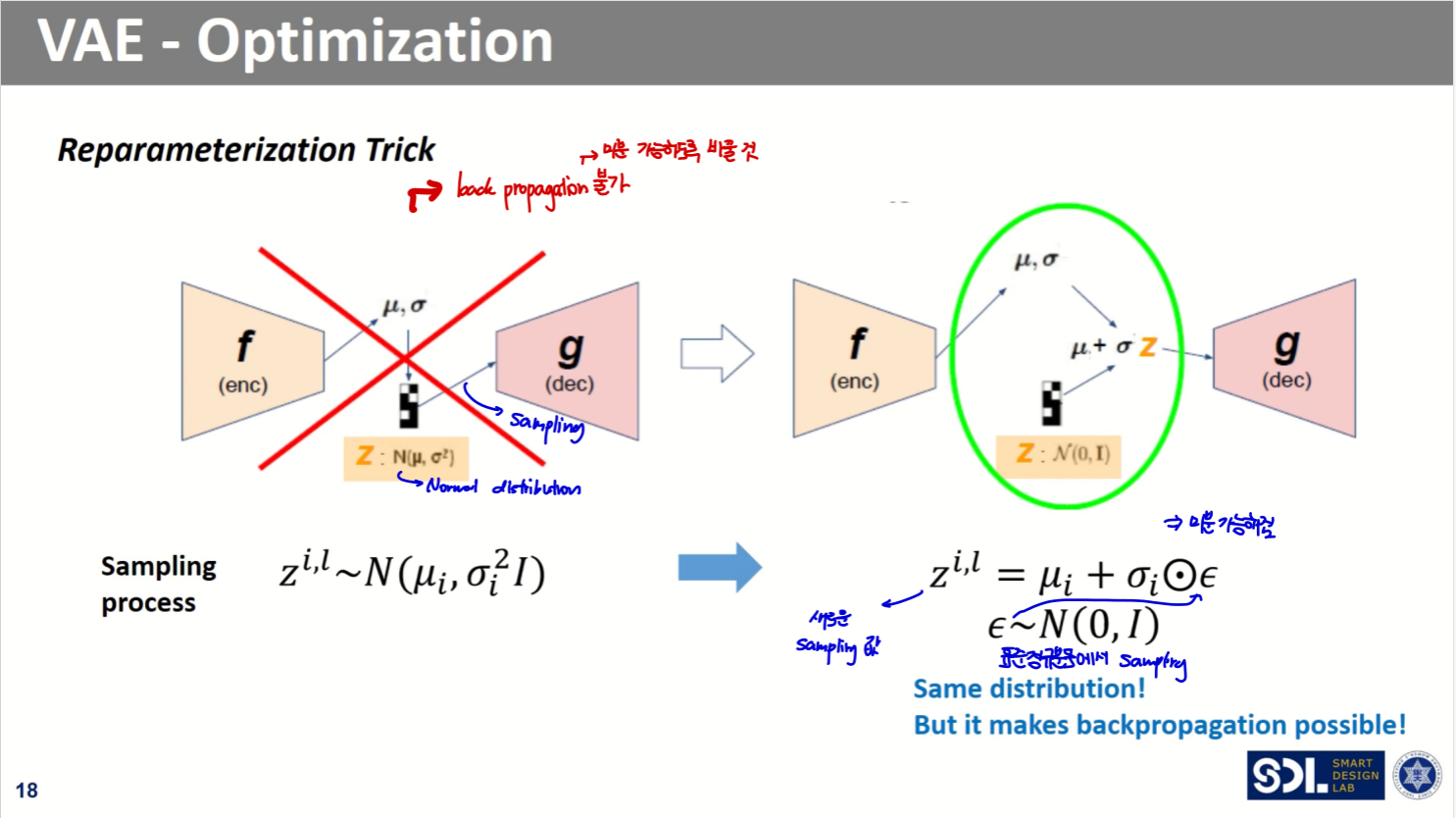
다시 돌아와서 Reconstruction Error 수식을 보면,
output의 분포 가정에 따라 수식이 바뀐다.
기본적으로 output이 Bernoulli 분포를 따른다고 가정하므로, 여기서는 Cross Entropy의 모습을 띈다.

output이 gaussian distribution을 따른다 가정할 경우, 위와 같이 MSE의 형태를 띈다.

VAE 정리

다시 돌아와서 모델 전체 구조를 보면 다음과 같다.

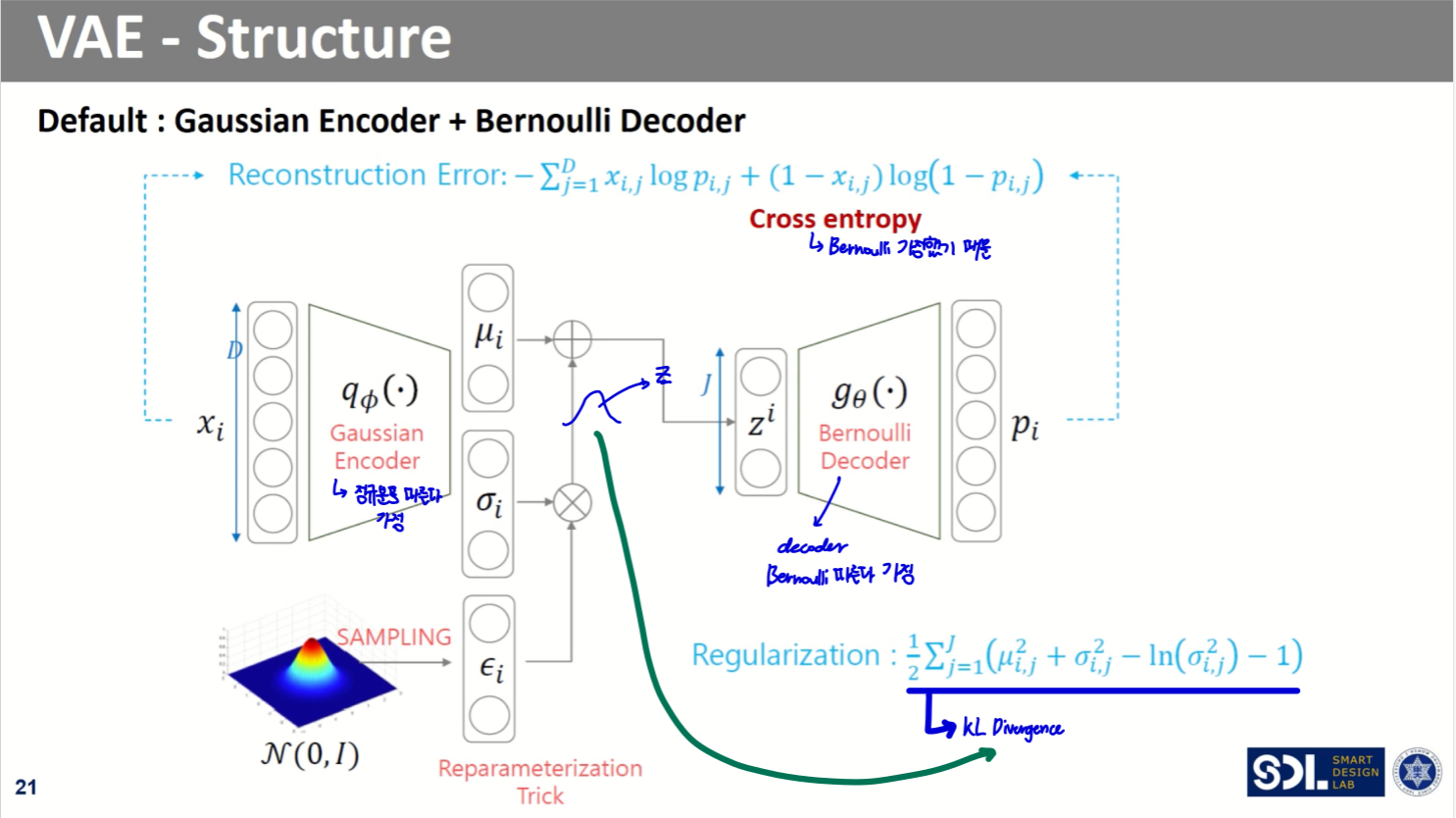
기본적으로 Gaussian Encoder와 Bernoulli Decoder를 가정한다.
이때 output에 대한 분포 가정이 달라질 경우, Reconstruction Error항이 바뀌게 된다.

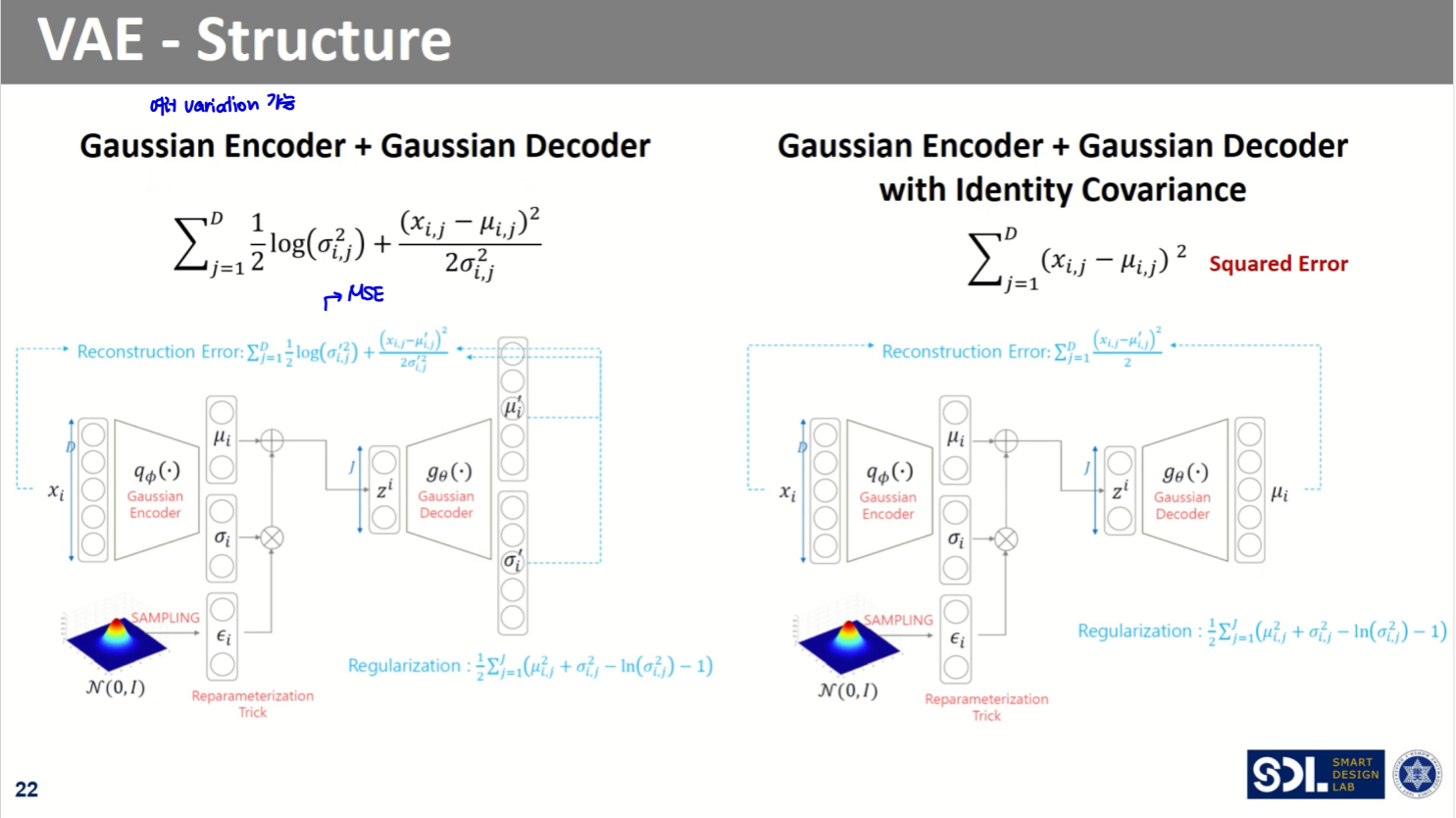
여러 형태로 variation이 가능하다!

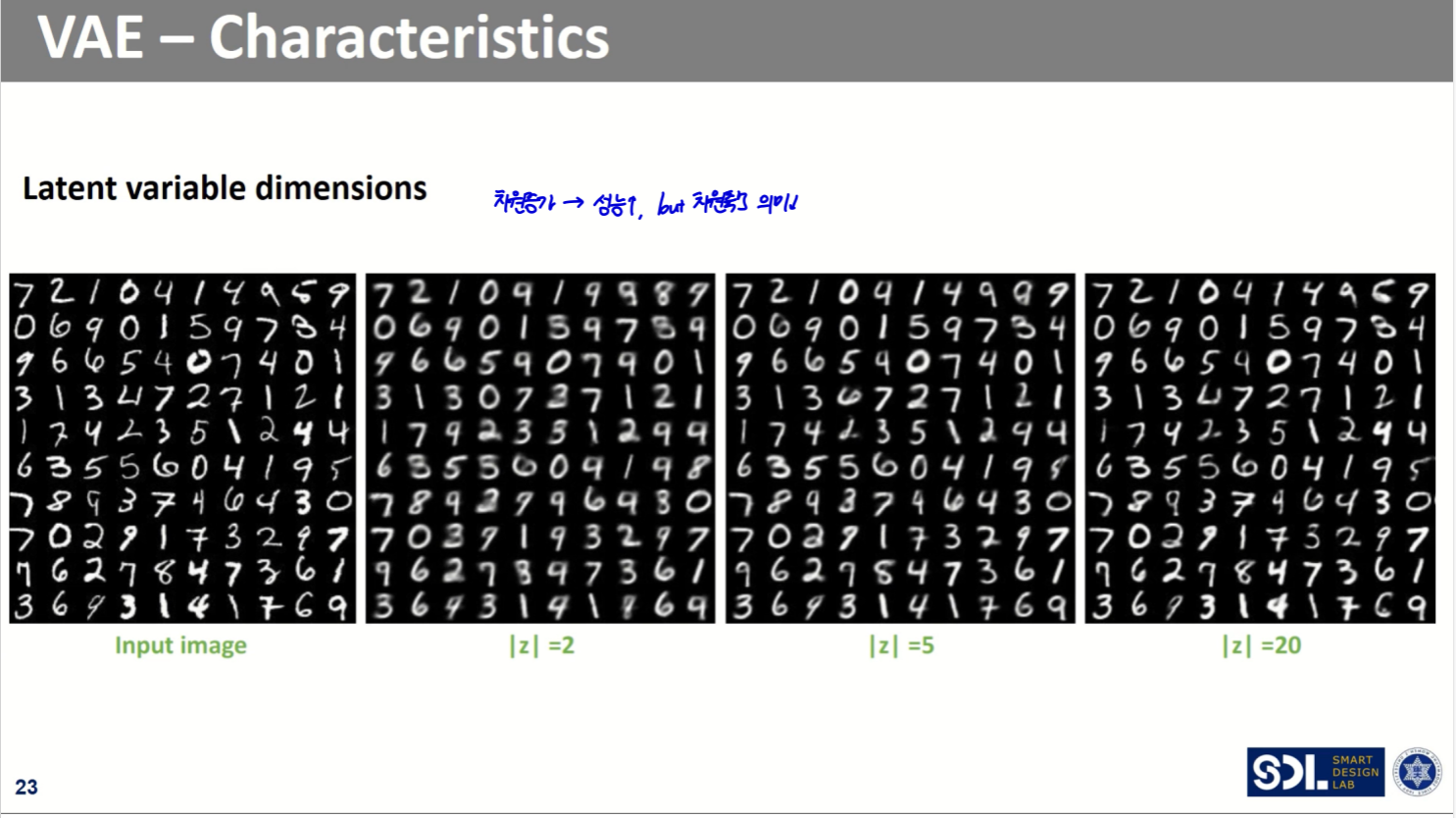
latent의 차원이 높아질 수록 복원 성능은 좋아지나, 차원축소의 의미가 작아진다.

VAE는 Decoder를 위해, 즉 생성을 위해 만들어졌으나 실제 연구에서는 Encoder로 많이 사용된다고 한다.
또한,

• Decoder가 '최소한' 학습 데이터는 생성해낼 수 있게 되므로, 생성된 데이터는 학습데이터와 닮아있다는 특징이 있다.
  • 아주 새로운 데이터를 생성해내지는 못한다.
• Encoder가 '최소한' 학습 데이터는 잘 latent vector로 표현할 수 있게 된다.
  • 데이터 추상화를 위해 많이 사용된다.