[MIT Deep Learning] CH12. Applications

전민진·2022년 2월 8일

Deep Learning

목록 보기

4/4

이번 챕터에선 딥러닝을 비전, 음성 인식, 자연어 처리 등 여러 응용 분야에 적용하는 방법을 살펴보자.

12.1 Large-Scale Deep Learning

오늘날까지, 신경망의 정확도와 신경망이 해결할 수 있는 과제의 복잡도를 개선하는데 있어 핵심적인 요인 하나는 신경망의 크기!
즉, 성공적인 딥러닝을 위해선 큰 신경망을 감당할 수 있는 고성능 하드웨어워 소프트웨어 기반 구조가 필요하다!

12.1.1 Fast CPU Implementations

예전엔 신경망을 컴퓨터 한 대의 CPU 하나를 이용해 훈련했지만, 요즘은 그런 접근 방식을 비효율적이라고 간주하는게 일반적! 대부분 GPU컴퓨팅을 이용하거나 여러 컴퓨터를 네트워크로 연결해 다수의 CPU를 활용한다.

특정 CPU 제품군에 맞춰 계산을 세심하게 구현하면 성능을 크게 개선할 수 있다.

2011년 최고 수준의 CPU기준으로, 부동소수잠(floating-point)산술 대신 고정소수점(fixed-point)산술을 이용하면 신경망의 작업을 좀 더 빨리 실행할 수 있었음

이렇게 수치 계산 코드를 세심하게 특수화 하거나 자료구조를 최적화해서 캐시 적중률을 높이는 것 혹은 CPU의 벡터 연산 명령어를 활용하면 성능이 크게 개선된다!

12.1.2 GPU Implementations

요즘 신경망을 구현할 땐 대부분 GPU에 의존한다. GPU는 원래 비디오 게임을 즐기는 소비자들의 수요에 의해 발생하고 성장했으나, 좋은 비디오 게임 시스템에 필요한 성능이 신경망에도 도움이 된다는 점이 밝혀졌다.

비디오 게임이 게임 속 장면을 효율적으로 렌더링하려면 수많은 연산을 병렬로 수행해야 한다. 그래픽 카드는 다수의 3차원 정점(3coordinates of vertices) 좌표들에 대해 행렬 곱셈과 나눗셈 연산을 수행함과 동시에, 이러한 3차원 좌표들을 2차원 화면 좌표로 변환하는 작업도 병렬로 수행해야 한다. + 각 픽셀에 대해 여러 연산을 적용해 픽셀의 값을 결정하는 연산도 병렬로 수행

GPU가 수행하는 작업의 특징

개별 계산이 단순
통상적인 응용 프로그램(CPU가 실행하는)에 비헤 조건 분기(branching)가 거의 없음

예를 들어, 어떠한 rigid object하나를 처리할 때, 그 rigid object의 모든 정점에는 동일한 행렬이 곱해짐. 정점마다 if문을 이용해 특정 행렬을 선택할 필요가 없음!
계산이 서로 완전히 독립적, 병렬화하기 쉬움
대량의 메모리 버퍼를 처리하는 과정이 관여

==> 그래픽 카드 제조사들은 전통적인 CPU에 비해 clock speed와 branching capability는 상대적으로 낮추고 대신 병ㄹ렬성과 메모리 대역폭을 높이는 쪽으로 GPU를 설계

신경망 알고리즘에서 GPU를 쓰는 이유

신경망에는 수많은 매개변수 값, 활성화 값, 기울기 값을 담은 큰 버퍼가 많이 쓰이고, 이를 학습시 각각 완전히 갱신해야함
경망 학습 알고리즘은 분기(braching)나 기타 복잡한 실행 흐름 제어가 많지 않음
신경망 각 층의 개별 뉴런을 각자 독립적으로 처리할 수 있음

GPGPU(general purpose GPU; 범용 GPU)기술이 등장하면서 신경망 학습을 위한 그래픽 카드의 인기가 폭발했다. GPGPU는 렌더링 서브루틴에 국한되지 않는 임의의 코드를 GPU에서 실행하는 기술이다.

NVIDIA는 GPGPU코드를 작성하기 위한 CUDA라는 프로그래밍 언어를 내놓았다. 하지만 GPGPU를 위한 효율적인 코드를 작성하는 것은 어려운 일이다. GPU에서 좋은 성능을 뽑아내는 데 필요한 기법들은 기존 CPU에 대한 것들과 아주 다르다!

예를 들어, CPU 기반 코드의 성능을 높일 때는 가능하면 캐시에서 최대한 많은 정보를 읽어 들이도록 코드를 설계할 때가 많다.

하지만 GPU에서 대부분의 쓰기 가능 메모리 장소들은 캐시에 저장되지 않으므로, 어떤 한 값을 한 번 계산해서 메모리에 저장한 후 다시 읽어 들이는 것보다는 그 값을 그냥 매번 계산하는 것이 더 빠를 수 있다.

GPU용 코드 작성시 주의 사항

GPU코드는 또한 본질적으로 다중 스레드 방식으로 작동하며, 서로 다른 스레드들의 실행을 세심하게 중재할 필요 O

예를 들어, 메모리 연산들은 합쳐져서(coalesce) 수행될 때 더 빠르다. 합쳐진 메모리 읽기 또는 쓰기 연산에 각 스레드에 필요한 어떤 값을 여러 스레드가 동시에,하나의 메모리 트랜잭션의 일부로 읽거나 쓸 때 발생한다.
일반적으로, i번째 스레드가 메모리의 i+j번째 바이트에 접근하되, j가 2의 거듭제곱의 배수인 패턴으로 대수의 스레드가 메모리에 접근할 때 메모리 연산들이 잘 합쳐진다.
==>(추가)캐시 불러올 때 그 정해진 범주를 정해, 그 크기 만큼의 데이터를 각 스레드마다 할당해 값을 불러오는 것! 그리고 나서 합침!(cuda가 이런 식으로 작동한다고 한다)
한 그룹의 각 스레드가 같은 명령을 동시에 수행하게 해야 한다는 것!

GPU의 스레드들은 워프(warp)라고 부르는 작은 그룹들로 분할된다. 한 워프의 각 스레드는 각 실행 주기(cycle)에서 동일한 명령을 수행하므로, 만일 같은 워프 안의 서로 다른 스레드가 서로 다른 코드 경로를 실행하야 한다면, 그 서로 다른 코드 경로들은 병렬이 아니라 순차적으로 실행된다.

고성능 GPU 코드를 작성하긴 어려우니까, 합성곱이나 행렬 곱셈 같은 고성능을 요구하는 연산들을 제대로 구현한 소프트웨어 라이브러리를 갖추고, 개별 모형에서는 그냥 그 라이브러리의 연산들을 호출하기만 하면 되게 하자!(Pylearn2, Theano, cuda-convnet, ThensorFLow, Torch 등)

12.1.3 Large-Scale Distributed Implementations

컴퓨터 한 대로는 큰 신경망을 실행하기에 부족할 때가 많으므로 학습 및 추론 작업을 여러 대의 컴퓨터로 분산하자!

추론(inference)의 분산은 간단하다. 그냥 각 입력 데이터를 각자 다른 컴퓨터로 처리하면 된다. $\rightarrow$ 자료 병렬성(data parallelism)

하나의 자료점(single datapoint)을 여러 대의 첨퓨터가 처리하게 하자. $\rightarrow$ 모델 병렬성(model parallelism)
이 경우 각 컴퓨터는 모델의 각자 다른 부분을 실행한다.

학습 과정에서는 자료 병렬성을 갖추는 것이 어렵다. 하나의 SGD(확률적 경사 하강법) 단계에 쓰이는 미니배치의 크기를 키우는 것이 한 방법이지만, 최적화 성능면에서 별로다. 이거보다 여러 컴퓨터가 여러 경사 하강 단계들을 병렬로 계산하게 하는 것이 더 좋지만, 순차적인 알고리즘이라 불가능하다.

한 가지 해결책은 비동기 확률적 경사 하강법을 사용하는 것이다. 비동기(asynchronous) 확률적 경사 하강법에서 각 코어는 lock 없이 매개변수들을 읽어서 기울기를 계산한 후 lock 없이 그 매개변수들을 갱신한다. 잠금을 적용하지 않으므로, 일부 코어가 다른 코어의 경과를 덮어쓸 수도 있다. 따라서 각 경사 하강 단계의 평균 개선량이 감소하나, 단계들의 산출 속도가 증가해 전체적으로는 학습이 좀 더 빨라진다. ❓ 와닿지가 않음..

12.1.4 Model Compression

상용 응용 프로그램에서는 기계 학습 모델을 학습하는데 필요한 시간과 메모리 비용을 낮추는 것보다 모델을 이용해 실제로 추론을 실행하는 데 필요한 시간과 메모리 비용을 낮추는 것이 훨씬 더 중요한 것들이 많다.
ex. 음성 인식 신경망을 강력한 컴퓨터 컬러스터에서 학습한 후 여러 사용자의 이동전화에 설치해 사용할 수 O

추론 비용을 줄이는 한 가지 핵심 전략은 모델 압축이다. 모델 압축 전략에선 원래의 고비용 모델을 더 작은, 저장 비용과 평가 비용이 낮은 모델으로 대체한다.

모델 압축은 주로 overfitting을 피하려고 크기를 키운 모델들에 적용할 수 있다.

대체로 독립적으로 훈련한 여러 모델로 구성된 앙상블 모델은 일반화 오차가 아주 낮다. 그러나 앙상블을 구성하는 신경망 n개를 모두 평가하려면 비용이 많이 든다. 그냥 모델의 하나의 크기를 키웠을 때(dropout으로 정규화해서) 일반화가 더 나아지는 경우도 있다.

큰 모델들도 작은 모델들처럼 어떤 함수 $f(x)$ 를 학습한다. 문제는, 학습 과정에서 과제에 필요한 것보다 훨씬 많은 매개변수가 쓰임.

근데 큰 모델을 쓰는 이유? 학습데이터가 충분하지 않은 것!

그래서, 일단 함수 $f(x)$ 에 모델을 fitting해서, 그 $f$ 를 무작위로 추출한 점들의 집합 $\mathbf{x}$ 에 넣어서 무한히 많은 데이터를 생성할 수 있다.

이후 이 데이터를 이용해서 더 작은 모델을 $f(x)$ fitting은 시키면 된다. 이 때, 새 모델의 수용력을 가장 효율적으로 활용하려면, 나중에 모델에 넣을 실제 테스트 입력들과 비슷한 분포로부터 새 $\mathbf x$ 를 추출하는게 좋다.
=> 이를 위해,

원래의 학습 데이터셋의 데이터들을 조금씩 변형해서 새 데이터들을 만듦
원래의 학습 데이터셋으로 학습한 생성 모형으로 데이터들을 생성

아니면, 더 작은 모델을 그냥 원래의 학습 데이터셋들로 학습하되, 모델의 다른 특징들을 복사하도록 학습할 수 있다.

12.1.5 Dynamic Structure

자료 처리 시스템의 속도를 높이는 방법 중 하나는 하나의 입력을 처리하는데 필요한 계산을 서술하는 계산 그래프에 동적 구조(dynamic structure)가 존재하는 시스템을 구축하는 것!

여러 신경망 중 주어진 한 입력의 처리에 알맞은 것들을 동적으로 선택할 수 O
개별 신경망 역시 입력에 있는 특정 정보를 계산하는 데 알맞은 부분(은닉 유닛들의 부분집합)을 동적으로 결정

신경망의 이런 동적 구조를 조건부 계산(conditional computation)이라고 부르기도 한다.

신경망에 적용되는 가장 단순한 형태의 동적 구조는 주어진 특정 입력에 적용할 신경망들의 한 부분집합을 동적으로 선택하는 것!

(흔치 않은 물체를 검출하는게 목표일 때) 중첩(cascade) 전략 사용

: 물체의 존재를 확실하게 검출하려면 수용력이 높은 정교한 분류기를 사용해야하는데, 이 경우 실행 비용이 높음. 그래서 이 때, 물체가 존재하지 않는 입력을 최대한 빨리 기각한다면 계산량을 줄일 수 있다.

이를 위해, 첫 분류기는 수용력이 낮은 모델을 사용한다. 그리고 이를 재현율(실제 positive인 데이터 중 몇 개나 맞췄는지)이 높게 나오도록 학습한다. 즉, 중첩의 첫 분류기는 물체가 존재하는 입력을 잘못 기각하는 일이 없도록 학습한다. 반면 마지막 분류기는 정밀도(모델이 positive라고 하는 데이터 중 몇 개나 맞는지)가 높도록 학습한다.
==> 테스트시, 불뉴기를 순서대로 실행해서 추론을 수행하되, 한 분류기라도 입력을 기각하면 입력에 대한 처리를 중단한다.
====> 이렇게 하면 물체의 존재를 확신도 높게 검출할 수 있으면서도 모든 데이터에 대해 완전한 추론 비용을 소비할 필요가 없다.

이러한 신경망 중첩이 높은 수용력을 가지게 하는 방법
- 중첩의 후반부에 있는 신경망들의 수용력을 개별적으로 높이는 것.
- 중첩의 개별 신경망은 수용력이 낮지만 그 신경망들의 조합은 수용력이 높게 만드는 것

스트리트 뷰 이미지에서 번지수 전사할 때, 2단계 중첩 사용
1. 하나의 기계 학습 모델을 시용해 이미지에서 번지수가 있는 영역을 특정
2. 또 다른 기계 학습 모델을 이용해 그 번지수의 숫자들을 전사

결정 트리 자체도 동적 구조의 예
: 각 노드는 자신의 여러 부분을 결정하기 때문.
게이터(gater)라고 부르는 신경망도 동적 구조를 가진 신경망의 예
:게이터는 여러 전문가망(expert network)중 하나를 선택해 현재 입력에 대한 출력을 계산

게이터는 expert network당 하나씩 여러 개의 확률 또는 가중치를 산출하고, 그 값의 가중 평균을 최종 결과로 출력한다.
이 경우에 게이터를 사용한다고 해서 계산 비용이 줄어들지는 않는다.

하지만 각 데이터에 대해 게이터가 하나의 expert network만 선택하도록 변경한 hard mixture of experts는 실제로 훈련 시간과 추론 시간을 상당히 줄여준다.
한 hidden unit이 다른 여러 unit 중 하나를 일종의 '스위치'를 통해서 적절히 선택해서 그 unit으로부터 입력을 받는 방식도 동적 구조의 예이다.
: 한 예로 attention mechanism이 있다.
하지만 요즘 쓰는 여러 가능한 입력들에 대해 가중 평균을 적용하는 접근 방식은 동적 구조가 제공하는 계산상의 이득이 없다.

동적 구조 시스템에서 발생하는 문제

시스템이 서로 다른 입력에 대해 서로 다른 코드 경로로 분기(branching)하다보니 병렬성이 줄어든다.
=> 데이터들을 실행 경로(분기)에 따라 여러 그룹으로 나누고, 그 데이터 그룹들을 동시에 처리함으로써 이런 문제점을 완화할 수도 있긴하다!

12.2 Computer Vision

컴퓨터 비전을 위한 대부분의 딥러닝 시스템은 어떤 형태이든 물체 인식 또는 물체 검출을 수행한다. 이러한 연구에서 생성 모델이 일종의 지도 원리(guiding principle)로 작용하기 때문에, 심층 모델을 이용해서 이미지를 합성하는 문제에 관해서도 많은 연구가 있었다. 이미지 합성 능력을 가진 모델은 이미지의 결함을 바로 잡거나, 이미지에서 특정 물체를 제거하는 등의 처리가 관여하는 이미지 복원(image resoration)에 주로 쓰인다.

12.2.1 Preprocessing

원본이 딥러닝 아키텍처가 표현하기 어려운 형태일 때가 많이 있다. 이런 경우엔 정교한 전처리가 필요하다!

하지만 일반적으로 비전에선 이런 종류의 전처리가 그리 필요하지 않다. 이미 입력 이미지의 모든 픽셀이 [0,1]이나 [-1,1]과 같은 적당한 범위로 정규화되어 있기 때문이다. 그렇지 않은 경우([0,1]과 [0,255]가 섞여 있는 경우)에 원본 이미지의 픽셀 값들의 scale을 통일하는 것이 필요하다.

또한, 비전 아키텍쳐에서 입력 이미지의 크기가 같아야 하기 때문에, 원본 이미지들을 그 크기에 맞게 잘라내거나 비례(확대, 축소)하는 과정이 필요하다.(물론 일부 모델은 가변 크기 이미지를 입력받을 수 있음)

data augmentation을 학습 데이터셋에만 적용하는 일종의 전처리로 볼 수 있다. 대부분의 비전 모델에서 data augmentation은 일반화 오차를 줄이는 탁월한 방법이다. 이를 테스트셋에 적용하는 방법 중 하나는, 모델에 같은 입력의 서로 다른 여러 버전을 보여줘서 각각 출력을 얻고, 그 출력들에 대해 다수결로 최종 출력을 산출하는 것!(앙상블)

학습 데이터셋과 테스트 데이터셋 모두에 적용할 수 있는 전처리들은 각 데이터를 좀 더 표준적인 형태로 변환해, 모델이 처리해야 하는 변동(variation)의 양을 줄이는 것이다.
=> 변동의 양을 줄여 학습 데이터셋에 fitting시켜야 할 모델의 일반화 오차와 크기가 모두 줄어든다!
=> 과제가 단순할수록, 더 작은 모델로 해결할 수 있고, 모델이 작아야 일반화가 잘 될 가능성이 높다.
(물론 데이터셋이 크면 필요하지 않음)

12.2.1.1 Contrast Normalization (명암비 정규화)

여러 비전 과제에서 안전하게 제거할 수 있는 가장 확실한 변동 요인은 마로 이미지의 명암비(contrast; 대비)이다.

명암비
: 이미지의 밝은 픽셀들ㅇ과 어두운 픽셀들의 차이가 어느정도인지 말해주는 값

딥러닝에선 흔히 이미지 전체 또는 한 영역의 픽셀들의 표준편차를 명암비로 간주.

입력 이미지 $\mathbf X \in \mathbb{R}^{r*c*3}$ , $\mathbf X_{i,j,k}$ 로 표기.(행 i, 열 j, k는 채널(RGB)을 의미)라 하면, 이때 이미지 전체의 명암비는 다음과 같다.

\sqrt{\frac{1}{3rc} \sum_{i=1}^{r} \sum_{j=1}^{c} \sum_{k=1}^3(\mathbf X_{i,j,k} - \bar{X}})

여기서 $\bar{X}$ 는 다음과 같이 정의되는 이미지 전체의 평균 세기이다.

\bar{X} = \sum_{i=1}^{r} \sum_{j=1}^{c} \sum_{k=1}^3\mathbf X_{i,j,k}

전역 명암비 정규화(global contrast normalization, GCN)
: 다수의 이미지들의 명암비 변동을 줄이기 위해, 각 이미지에서 평균 명암비를 뺀 후 이미지 픽셀들의 표준편차가 어떤 축척 상수 $s$ 와 같아지도록 적절히 스케일링한다.

한 가지 문제점은 명암비가 0인 이미지(모든 픽셀이 같은 세기인 이미지)는 그 어떤 비례 계수를 써도 명암비를 변경할 수 없다는 것.명암비가 아주 낮지만 0은 아닌 이미지는 이미지에 담긴 정보가 거의 없을 때가 많다. 이 경우 진 표준편차로 나누어 봤자 잡음이나 압축에 의한 결함만 더 강조된다!(작은 수로 나누면 더 증폭되니까)
==> 그래서 작은 양의 정규화 매개변수 $\lambda$ 를 표준편차 추정량에 더하거나 분모가 $\epsilon$ 이상이 되어야 한다는 제약을 도입

두 방법을 모두 적용했을 때, 입력 이미지 $\mathbf X$ 에 대해 GCN이 출력하는 이미지 $\mathbf X'$ 는 다음과 같이 정의된다.

$\mathbf X' = s \frac{\mathbf X_{i,j,k} - \bar{X}}{max \{ \epsilon , \sqrt{\lambda + \frac{1}{3rc} \sum_{i=1}^{r} \sum_{j=1}^{c} \sum_{k=1}^3(\mathbf X_{i,j,k} - \bar{X}})^2\}}$
- 관심 대상 물체만 cropping한 이미지로 이뤄진 데이터셋의 경우 픽셀들의 세기가 거의 일정한 이미지는 별로 없다.
  ==> $\lambda=0$ 또는 아주 작은 값의 $\epsilon$ 사용.
- 무작위로 cropping한 작은 이미지들은 픽셀 세기가 일정할 가능성이 더 크다
  ==> $\lambda=10$ , $\epsilon=0$ 사용
- 축적 상수 $s$ 는 그냥 1로 두거나 모든 데이터의 픽셀값 표준편차가 1에 가깝게 되는 값으로 설정하는 것이 일반적

GCN을 데이터들을 하나의 구의 표면에 있는 점들에 맵핑하는 사상이라고 생각할 수 있다! 이러한 구면 사상은 신경망이 공간의 구체적인 위치보다는 상대적인 방향에 더 잘 반응할 때가 많다는 점에서 유용하다.

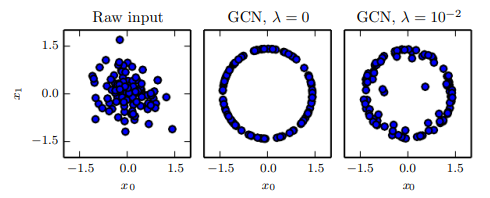
신경망이 원점으로부터 방향이 같고, 거리가 서로 다른 점들에 반응하려면, 기저는 다르지만 동일 선상에 놓인 가중치 벡터들을 가진 은닉 단위들이 필요. ❓ 이런 상황은 학습 알고리즘이 발견하기 어려울 수 있다. GCN은 각 데이터를 하나의 방향과 하나의 거리의 조합이 아니라 하나의 방향으로 축약하므로써 이러한 문제를 피한다.

** 구면화(shering)라는 전처리는 GCN과는 다르다! 구면화는 자료를 구면으로 사상하는게 아니라 분산이 같아지도록 주성분들을 재비례하는 것. (== whitening과 같은 연산)

GCN은 윤곽선이나 모퉁이처럼 좀 더 뚜렷하게 나타나면 좋은 이미지 특징을 강조하지 못할 때가 많다(ex. 어두운 영역 안의 윤곽선들이 두드러지게).

이를 해결하기 위해 사용하는 것이 LCN(local contrast normalization; 국소 명암비 정규화)!

국소 명암비 정규화(local contrast normalization, LCN)
: 이미지 전체가 아니라 이미지의 작은 영역들에 대해 명암비를 정규화
```
 >LCN과 GCN의 차이가 나타나는 그림.
```
LCN의 방법은 여러 가지이지만, 각 픽셀에서 인근 픽셀들의 평균을 빼고, 인근 픽셀들의 표준편차로 나누는 것은 모든 방법에서 공통적이다. 또한 GCN처럼 LCN에서도 0으로 나누기를 피하기 위해 정칙화를 적용할 필요가 있다.

12.2.1.2 Data augmentation

분류기의 일반화를 손쉽게 개선하는 한 방법은 부류(class)를 변경하지 않는 변환들로 학습 데이터셋들을 수정해 얻은 새 데이터들로 학습 데이터셋의 크기를 키우는 것.

이 방법은 특히 물체 인식과 잘맞는다. 물체 인식을 위한 분류기의 경우 무작위 이동 변환과 회전 변환으로 데이터들을 생성해 일반화를 개선할 수 있다. 그리고 특화된 비전 응용 분야에선 그보다 더 정교환 변환들, 이미지의 색상들을 무작위로 섭동하거나 입력에 비선형 기하 왜곡 변환을 적용하는 등의 방법이 data aumentation에 흔히 쓰인다.

12.3 Speech Recognition

음성 인식의 과제는 자연어 발화(utterance), 즉 입 밖으로 나온 말을 담은 음향 신호를 화자가 의도한 단어들의 순차열로 사상하는 것!

음향 입력 벡터들(보통 음향 데이터를 20ms 길이의 프레임들로 분할)의 순차열을 $\mathbf{X} = (x^{(1)},x^{(2)},..,x^{(T)})$ 라고 표기하도록 하자. 이후 목표 출력 순차열(문자열 혹은 단어열)을 $\mathbf{y} = (y_1,y_2,..,y_N)$ 으로 표기하기로 하자.

자동 음성 인식(automatic speech recognition, ASR)은 주어진 음향 정보 순차열 $\mathbf{X}$ 에 대응되는 가장 그럴듯한 언어 정부 순차열 $\mathbf{y}$ 를 계산하는 함수 $f^*_{ASR}$ 을 학습하는 것을 목표로 한다.

f^*_{ASR}(\mathbf{X}) = \underset{\mathbf y}{\arg\max} P^*(\mathbf y|X = \mathbf X)

여기서 $P^*$ 는 입력 $\mathbf X$ 를 목표 $\mathbf{y}$ 와 연관시키는 진(true) 조건부 분포!

1980년대부터 약 2012년까지, 최고 수준의 음성 시스템들은 기본적으로 은닉 마르코프 모형(hidden Markov model, HMM)과 가우스 혼합 모형(Gaussian mixture model, GMM)의 조합이었다.

GMM과 HMM의 조합에 해당하는 부류의 학습 모델들은 처리할 음향 파형 데이터가 다음과 같는 과정으로 생성되었다고 가정한다.
1. HMM이 음소들과 이산적인 부분음소 상태들(한 음소의 초성, 중성, 종성 등)의 순차열을 산출한다.
2. GMM이 그러한 각 이상적 기호들을 짧은 길이의 음형 파형 데이터로 변환한다.
최근까지는 이러한 GMM-HMM조합 시스템이 ASR분야를 주도했지만, 음성인식은 신경망이 최초로 적용된 응용 분야 중 하나이다.

이후 더 훨씬 더 크고 깊은 모델과 데이터셋을 사용할 수 있게 되면서, 음향 특징들을 음소들에 연관시키는 과제를 GMM대신 신경망이 맡게 되었다. 2009년부터는 비지도 학습에 기초한 일종의 딥러닝 기법을 음성 인식에 적용!

제한 볼츠만 기계(RBM)라고 부르는 undirected 확률적 모델을 학습해 입력 자료를 모델화하는 것에 기반

음성 인식 과제를 해결하기 위해, 먼저 비지도 사전 훈련(unsupervised pretraining)을 이용해 하나의 심층 순방향을 구축하는데, 이 때 신경망의 각 층을 하나의 RBM의 훈련을 통해서 초기화. 이 신경망은 고정 크기 입력 구간(한 프레임 단위)안의 음향 스펙트럼 표현을 입력받아서, 그 구간의 중심 프레임에 대한 HMM 상태들의 조건부 확률을 예측.
=> 이 결과 TIMIT에 대한 인식률 크게 증가, 음소 오차율도 26%에서 20.7%로 낮아졌다.

이후 시간이 지나면서, 음성 인식을 위한 딥러닝은 결국 사전학습과 볼츠만 기계에 기초한 모형에서 rectified linear unit와 dropout 같은 기술들에 기초한 모델로 넘어가게 되었다.

주요 혁신 중 하나는 합성곱 신경망을 이용해 시간과 주파수 모두에 대해 가중치들을 복제하는 것. 그런 신경망은 시간ㅇ ㅔ대해서만 가중치를 복사했던 기존의 시간 지연 신경망보다 더 나은 성과를 낸다. 새로운 2차원 합성곱 모델은 입력 스펙트로그램을 긴 벡터가 아니라 일종의 2차원 이미지로 취급하는데, 입력 이미지의 축은 시간, 다른 축은 스펙트럼 구성 요소들의 주파수에 대응 된다.

현재도 지속되고 있는 연구는 HMM을 아예 빼버리고 처음부터 끝까지 심층망으로 이뤄진 'end-to-end deep learning ASR'을 구축하는 것이다.