Deep Learning

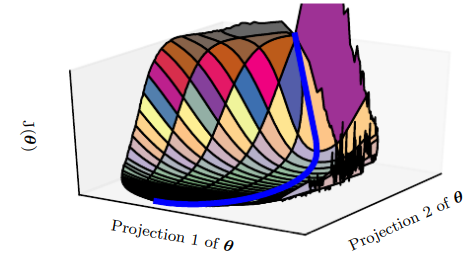
이번 챕터에서는 신경망 네트워크 학습에 사용되는 최적화 기법들을 소개한다. 특히, 비용 함수 $J(\\theta)$를 크게 감소시키는 신경망 네트워크의 파라미터 $\\theta$를 찾는 것에 초점이 맞춰져 있다.우선 머신러닝을 학습할 때 사용되는 최적화와 순수 최적화가

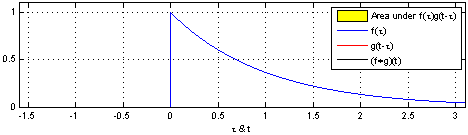
합성곱 : 두 함수를 곱해서 더함.어떻게 두 함수를 곱해서 더할까?$$ (f\*g)(t) = \\int^{\\infty}\_{-\\infty}f(\\tau)g(x-\\tau)d\\tau$$1 . 우선 합성곱을 위해선 두 함수 중 하나를 반전 2\. 반전시킨 함수를

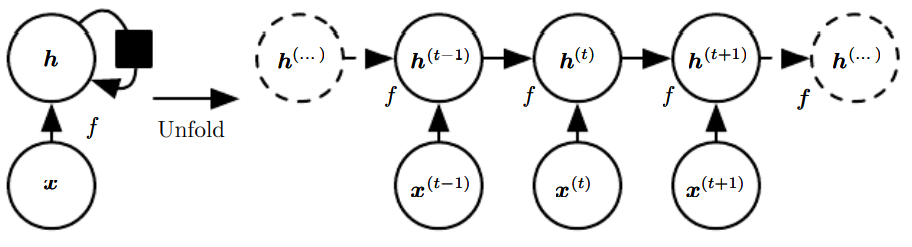
순환 신경망(recurrent neural networks, RNN)은 순차적인 자료를 처리하는 신경망의 한 종류이다.순차열(sequence), 즉 순서 있는 일련의 값들 $x^{(1)},...,x^{(\\tau)}$을 처리하는 데 특화더 긴 순차열로 손쉽게 확장할 수

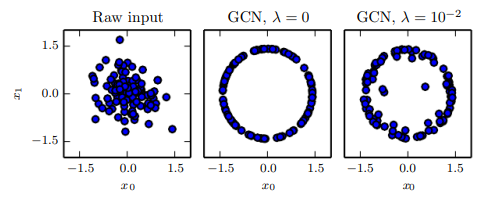
이번 챕터에선 딥러닝을 비전, 음성 인식, 자연어 처리 등 여러 응용 분야에 적용하는 방법을 살펴보자.오늘날까지, 신경망의 정확도와 신경망이 해결할 수 있는 과제의 복잡도를 개선하는데 있어 핵심적인 요인 하나는 신경망의 크기!즉, 성공적인 딥러닝을 위해선 큰 신경망을