[MIT Deep Learning] CH10. Sequence Modeling : Recurrent and Recursive Nets

순환 신경망(recurrent neural networks, RNN)은 순차적인 자료를 처리하는 신경망의 한 종류이다.

• 순차열(sequence), 즉 순서 있는 일련의 값들 $x^{(1)},...,x^{(\tau)}$을 처리하는 데 특화
• 더 긴 순차열로 손쉽게 확장할 수 있고, 대부분 가변 길이 순차열도 처리할 수 있음
• 매개변수들을 공유
  • 다층 신경망 형태가 서로 다른(길이가 서로 다른) 데이터의 모형에 확장, 데이터에 대해 다층 신경망을 일반화 할 수 있음
  • 시간 색인의 각 값에 대해 매개변수를 따로 둔다면, 학습 과정에서 경험하지 않은 길이의 순차열들에 대해 신경망을 일반화 할 수 없다.

    특정한 정보가 순차열 안의 여러 지점에서 출현할 수 있을 경우에 특히 중요해짐.
    "I went to Nepal in 2009"와 "In, 2009. I went to Nepal"이라는 문장에서 화자가 네팔에 간 해를 파악해야 한다고 했을 때, 모델은 2009가 어디에 있든 중요하다는 것을 인식해야한다. => 가중치 공유가 중요!

** 순환마디(cyle) : 한 변수의 현재 값이 미래의 한 시간 단계의 자신의 값에 영향을 미치는 구조

10.1 Unfolding Computation Graphs

** unfolding = 재귀적인 또는 순환적인 계산을 펼쳐서 반복 구조를 가진 계산 그래프 형태를 얻음

순환 신경망의 은닉 유닛은 다음과 같이 표현할 수 있다.

전형적인 RNN은 기본 식에 상태 $h$에 담긴 정보를 읽어서 예측값을 산출하는 출력층 같은 추가적인 구성요소가 더해진 형태!

과거로부터 미래를 예측하도록 RNN을 학습시킬 때는 $h^{(t)}$를 일종의 손실 있는 과거 요약 함수, 즉 t까지의 지난 입력 순차열을 요약하는 함수로 활용할 때가 많다. 일반적으로 이러한 요약 함수는 임이의 길이의 순차열($x^{(t)},x^{(t-1)}...,x^{(1)}$을 고정 길이 벡터 $h^{(t)}$에 사상하기 떄문에, 손실이 있을 수 밖에 없다.
=> 시간에 따라 중요도를 다르게 하여, 일부 상태를 다른 상태보다 더 높은 정밀도로 유지할 수 있다.

예를 들어, 통계적 언어 모형에 RNN을 적용하는 경우, 시간 t까지의 입력 순차열의 모든 정보를 저장할 필요 없이 문장의 나머지 부분을 예측하는 데 충분한 정보만 저장하면 될 수도 있다.

앞서 표현한 순환 신경망의 식을 도식화 하는 방법은 크게 두 가지이다.

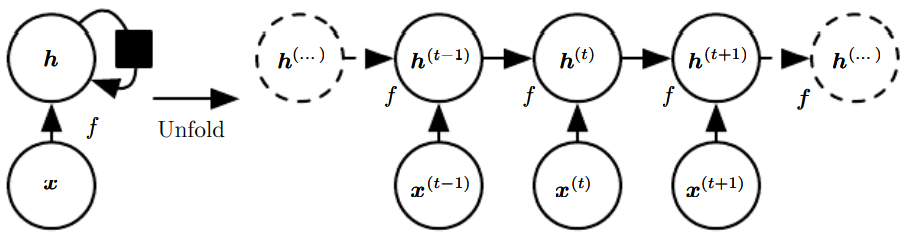
왼쪽을 오른쪽처럼 반복 요소들이 있는 그래프로 만드는 것이 앞에서 언급한 펼치기 연산에 해당한다.

t단계로 펼쳐진 점화식을 다음과 같이 $g_{(t)}$라는 함수로 표현할 수 있다.

함수 $g^{(t)}$는 전체 과거 순차열$x^{(t)}, x^{(t-1)},... ,x^{(1)}$을 받아서 현재 상태를 산출한다. 이를 함수 $f$를 여러 번 적용한 상태로 분해할 수 있고, 이는 2가지 장점을 제공한다.

• 학습된 모형은 길이가 가변적인 상태 역사(과거 상태들의 순차열)가 아니라 한 상태에서 다른 상태로의 전이(transition)를 명시하므로, 그 입력 크기는 순차열의 길이와는 무관하게 항상 동일 ❓
• 모든 시간 단계에서 동일한 전이 함수 $f$를 동일한 매개변수들과 함께 적용하는 것 가능

이 두 요인 덕에 하나의 모형 $f$가 모든 시간 단계와 모든 순차열 길이를 지원하게 만들 수 있다. 하나의 공유 모형을 학습하면, 모형은 학습 데이터셋에 없던 길이의 순차열들로도 일반화 된다! + 훨씬 적은 수의 학습 데이터셋으로도 모형을 추정할 수 있음.

10.2 Recurrent Neural Netwokrs

다음은 순환 신경망의 설계에서 자주 볼 수 있는 중요한 패턴이다. 이 셋 중에서는 첫번째가 가장 대표적이다.

• 각 시간 단계에서 하나의 출력을 산출하며, 은닉 유닛들 사이에 순환 연결들이 존재하는 순환 신경망
  
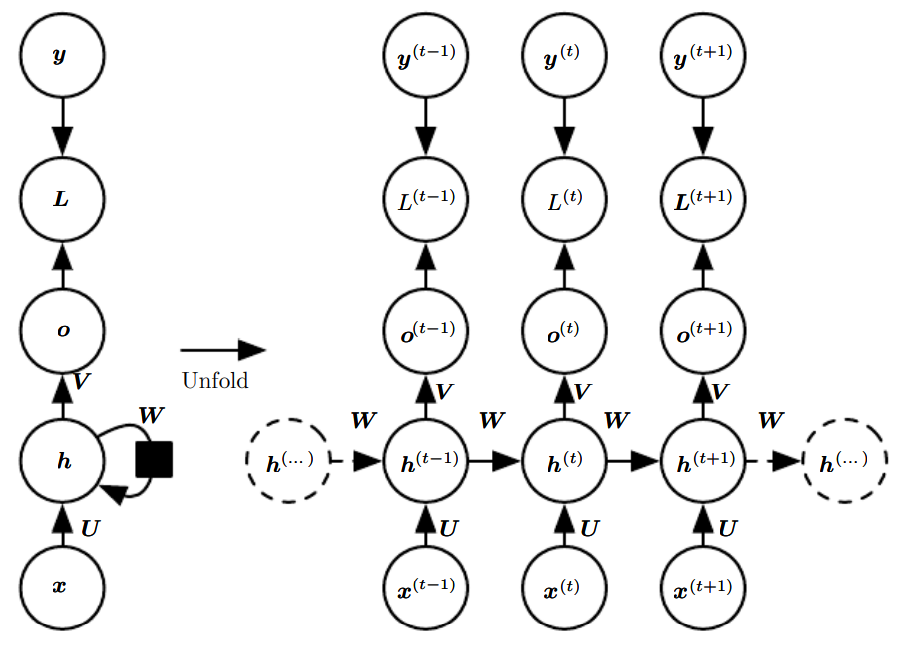
• 각 시간 단계에서 하나의 출력을 산출, 한 시간 단계의 출력과 그다음 시간 단계의 은닉 유닛들 사이에만 순환 연결들이 존재하는 순환 신경망
  
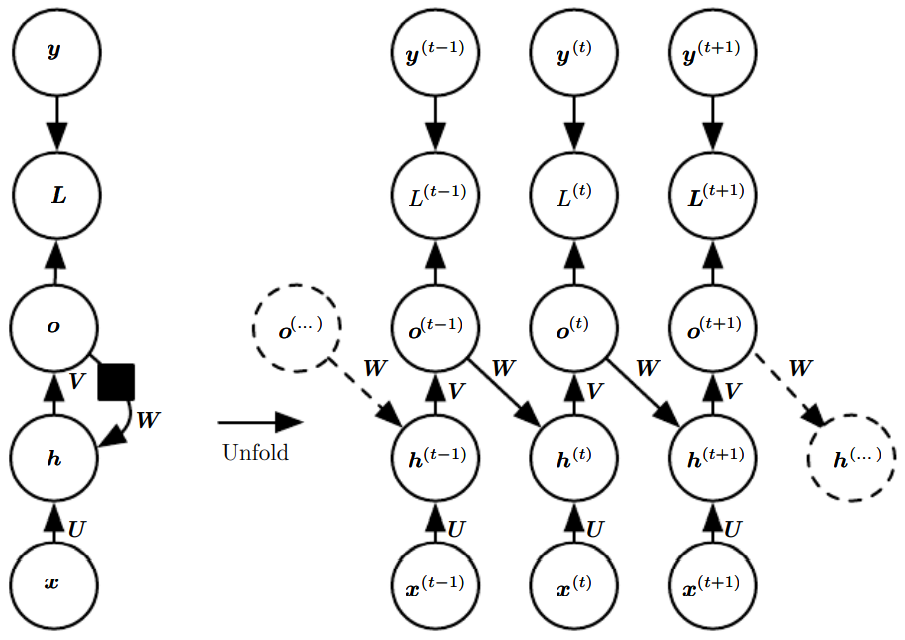
• 은닉 단위들 사이에 순환 연결들이 존재하고, 순차열 전체를 읽어서 하나의 출력을 산출하는 순환 신경망
  

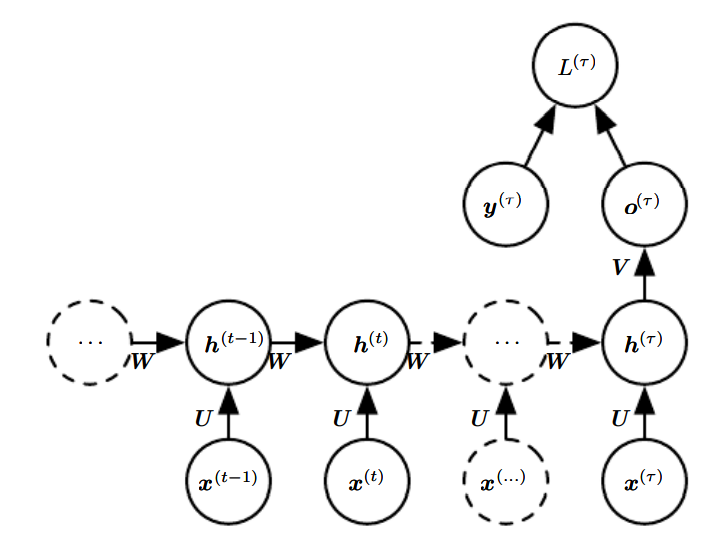
첫 번째 그림에 해당하는 RNN의 순전파 공식을 만들어보자. 그림에는 은닉 유닛들에 쓰인 활성화 함수가 구체적으로 명시되어 있지 않지만, $tanh$ 활성화 함수를 사용한다고 가정하겠다. 또한 출력은 이산적, 후처리 단계에서는 소프트맥스를 적용하도록 하겠다.

여기서 bias $b$,$c$와 입력 대 은닉, 은닉 대 출력, 은닉 대 은닉 연결에 대한 가중치 행렬 $U,V,W$이다.

주어진 $x$값들의 순차열과 그에 대응하는 $y$값들의 순차열에 대한 총 손실함수는 모든 시간 단계에서의 손실값들의 총합으로 두면 된다. 예를 들어, $L^{(t)}$가 주어진 $x^{(1)},...,x^{(t)}$에 대한 $y^{(t)}$의 음의 로그가능도라고 하면, 그러한 총 손실함수는 다음과 같이 정의된다.

이 때, 이 손실함수의 매개변수들에 대한 기울기를 계산하려면 비용이 많이 든다. 기울기를 계산하려면 위의 그림에서 펼쳐진 그래프를 왼쪽->오른쪽으로 훑는 순전파 과정과 다시 오른쪽->왼쪽으로 훑는 역전파 과정이 필요하다. 이 때 실행시간은 $O(\tau)$인데, 병렬화로 더 줄일 수 없다. 또한 순전파 과정에서 계산한 상태들을 모두 저장한다면 역전파 과정에서 재사용해야 하기 때문에 메모리 비용 역시 $O(\tau)$이다.

10.2.1 Teacher Forcing and Networks with Output Recurrence

한 시간 단계에서 출력과 그다음 시간 단계에서의 은닉 단위들 사이에만 순환 연결이 존재하는 신경망(두번째 그램)은

• 은닉 대 은닉 순환 연결이 없어 표현력이 약하다
  (보편 튜링 기계를 흉내 내지 못함.)
• 신경망이 미래를 예측하는 데 사용할 과거의 모든 정보를 출력 단위들이 포착해야 함.
  (하지만 출력 단위들은 학습 데이터셋의 목표값과 부합되게 학습 되므로, 입력의 과거에 대한 필수 정보를 출력 유닛이 포착할 가능성은 작다)

그럼에도 장점 역시 존재한다.

• 손실함수가 시간 $t$에서의 예측과 시간 $t$에서의 학습 목표값의 비교에 기초하는 경우, 은닉 대 은닉 순환 연결이 없으면 모든 시간 단계를 분리해 각 단계 $t$에서의 기울기를 개별적으로 계산하는 것이 가능
  => 현재 출력을 계산하기 위해 이전 시간 단계의 출력을 먼저 계산할 필요 없음. 병렬화 가능!
  (이게 그 어차피 그 전 단계의 출력값을 받을건데, 걔는 어차피 학습데이터의 y에 근사하도록 학습할거니까 앞 단계가 안끝나도 y를 집어낳으면 되니까 병렬이 된다는 건가?)

출력에서 모델의 내부로 돌아가는 순환 연결이 있는 모델엔 교사 강제(teacher forcing)라는 학습 기법을 적용할 수 있다. 교사 강제는 모델을 학습하는 과정에서 출력 참값 $y^{(t)}$을 시간 $t+1$에서의 입력으로 사용한다.

이 예에서, $t=2$일 때 모형은 지금까지의 순차열 $x$와 학습 데이터셋의 이전 목푯값 $y$ 둘 다 주어졌을 때의 $y^(2)$의 조건부 확률을 최대화하도록 훈련된다.
==> 최대가능도는 이러한 연결들에 정확한 출력이 무엇이어야 하는지를 알려주는 목표값들을 입력해야 한다는 것을 학습 도중에 명시한다(모형의 출력을 다시 넣는 것이 아님!)

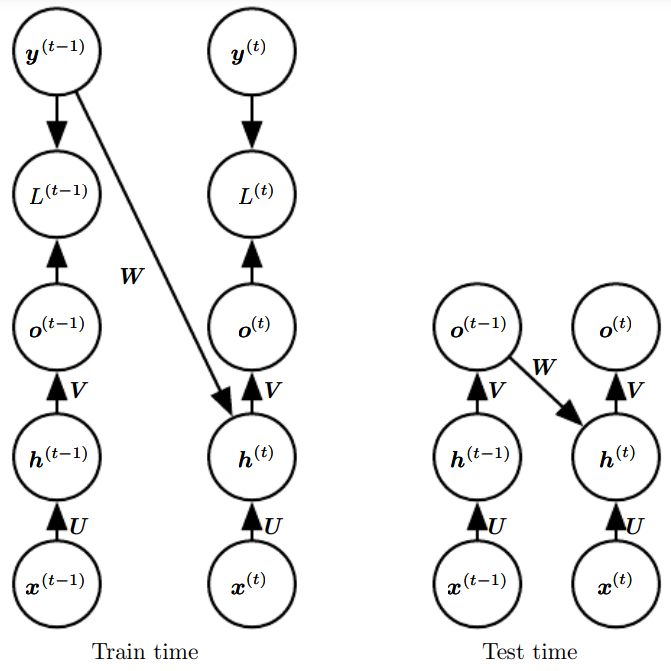
이와 같이 교사 강제는 은닉 대 은닉 연결이 없는 모델에서 시간 역전파(BPTT)를 피하는 한 방법이지만, 은닉 대 은닉 연결이 있는 모델이라도 한 시간 단계의 출력에서 그다음 시간 단계에서 계산되는 값들로 가는 연결이 존재한다면, 교사 강제를 적용할 수 있다. 단, 은닉 단계가 이전 시간 단계의 함수가 되면 BPTT알고리즘 필수가 되므로 교사 강제와 BPTT 모두로 학습하는 모델도 존재한다.

엄격한 교사 강제의 단점은 신경망을 나중에 열린 루프(open-loop) 모드로 사용하게 될 때 드러난다.

열린 루프란?
: 신경망의 출력을 다시 입력으로 되먹이는 것을 말한다.

이 경우, 학습 과정에서 신경망이 경험하는 입력들의 종류와 시험 과정에서 신경망이 경험하는 입력들의 종류가 상당히 다를 수 있다.

==> 이 문제를 완화하기 위해 교사 강제를 적용할 때의 입력과 자유 실행 시의 입력 모두로 신경망을 훈련하는 것이다.

예를 들어, 펼쳐진 순환 출력 대 입력 경로를 따라 몇 시간 단계 이후의 미래의 정확한 목푯값을 예측한다면, 그런 훈련이 가능하다. 이 방법을 적용하면 신경망은 학습 과정에서 경험하지 못한 입력 조건들(자유 실행 모드에서 모형 자신이 생성한 입력 등)을 고려해서 상태를 신경망이 몇 단계 후에 적절한 출력을 생성하게 하는 상태로 다시 사상하는 방법을 배운다.
❓ 이게 그 중간 중간에만 정답으로 에러를 추정해서 둘다 쓴다는 말인가?

==> 또는 생성된 값들을 입력으로 사용할지 실제 y값을 입력으로 사용할지를 무작위로 선택하는 것. 생성된 값들을 점점 더 ㅁ낳이 입력으로 사용하는 커리큘럼 학습 전략을 활용

10.2.2 Computing the Gradient in a Recurrent Neural Network

순환 신경망에서 기울기를 계산하는 것은 간단하다. BPTT 알고리즘의 작동 방식을 이해하는 데 도움이 되도록, 앞에 나온 RNN공식들에 대해 BPTT로 기울기를 계산하는 예를 살펴보자.

이 예의 계산 그래프는 파라미터 $U,V,W,b,c$에 대한 노드들과 순차열 $x^{(t)},h^{(t)},o^{(t)},L^{(t)}$에 대한 $t$를 인덱스로 하는 노드들로 구성된다. 각 노드 $N$에 대해 기울기 $\nabla_{N}L$을 재귀적으로 계산해야 한다.

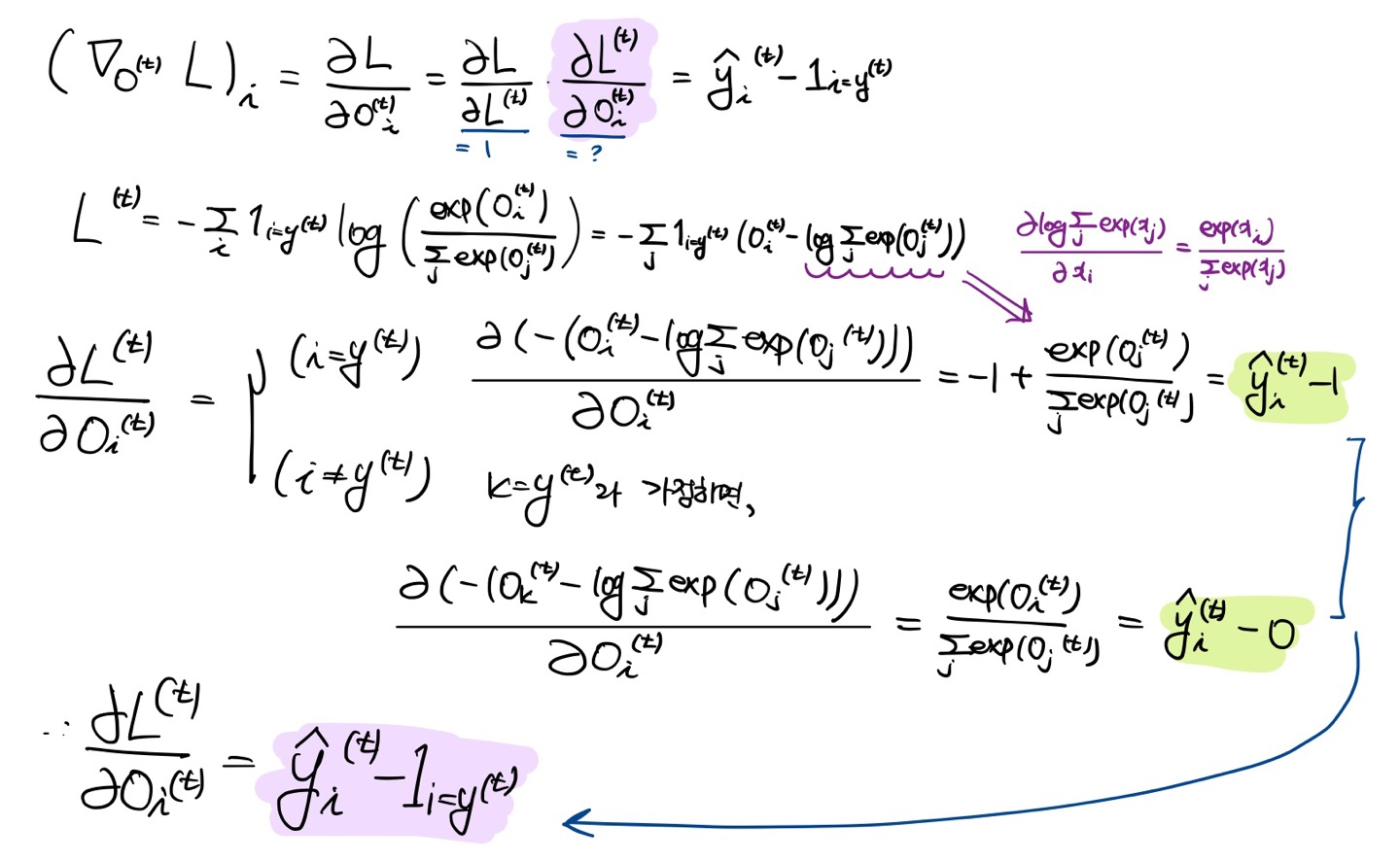
우선, 최종 손실값 바로 전의 노드로 재귀를 시작한다. 그 노드의 기울기는 다음과 같다.

이 예에서는 신경망의 출력 $o^{(t)}$을 소프트맥스 함수의 인수로 사용해서 출력에 관한 확률들의 벡터 $\hat{y}$를 얻는다 가정한다. 또한, 손실값이 지금까지 입력에 대한 실제 찐 목표값 $y^{(t)}$의 음의 로그가능도라고 가정한다. 모든 $i,t$에 대해, 시간 단계 $t$에서의 출력들에 대한 기울기 $\nabla_{o^{(t)}}L$은 다음과 같다.

(** 소프트맥스 미분하면 됨 아래 그림 참조)

이 계산은 재귀적으로, 즉 순차열의 끝에서 시작해서 거꾸로 진행된다. 마지막 시간 단계 $\tau$에서 후행 노드는 $o^{(\tau)}$뿐이므로, 기울기는 다음과 같이 간단ㄷ하다.

이제 $t=\tau-1$에서 $t=1$로 시간을 거슬러 올라가면서 기울기들을 역전파한다. 이 때부터는($t<\tau$에 대해서는) $o^{(t)}$뿐만 아니라 $h^{(t+1)}$도 $h^{(t)}$의 후손이다. 따라서 기울기는 다음과 같이 주어진다.

$diag(1-(h^{(t+1)^2}))$은 성분 $1-(h^{(t+1)})^2$들을 담은 대각행렬을 뜻한다. 이는 시간 $t+1$에서의 은닉 유닛 i와 연관된 쌍곡탄젠트의 야코비 행렬이다.

계산 그래프의 내부 노드들에 대한 기울기들을 계산한 후에는 매개변수 노드들에 대한 기울기를 계산할 수 있다. $\nabla_{W^{(t)}}$는 시간 단계 $t$에서 가중치들이 기울기에 기여하는 정도를 나타낸다.
이러한 표기법을 이용해 나머지 파라미터들의 기울기를 표현한 것은 다음과 같다.

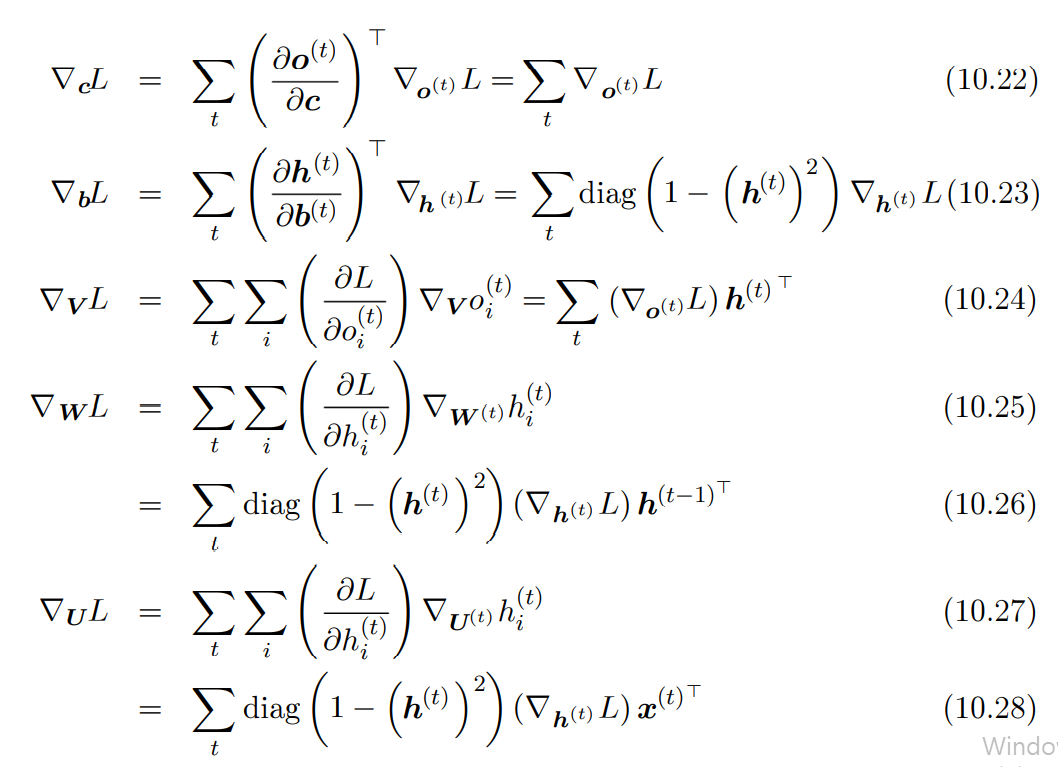
10.2.3 Recurrent Networks as Directed Graphical Models

지금까지 살펴 본 순환 신경망의 손실함수 $L^{(t)}$는 학습 목표 $y^{(t)}$와 출력 $o^{(t)}$사이의 교차 엔트로피이다. 하지만 순환 신경망도 이론적으로 거의 모든 종류의 손실함수를 지원한다. 손실함수는 태스크에 맞게 선택해야 한다.

• 출력을 하나의 확률분포로 해석하는 것이 바람직할 때
  => 교차 엔트로피

  예를 들어, 순방향 신경망에서처럼, 출력 분포가 표준 정규 분포일 때 그와 연관된 교차 엔트로피 손실은 평균제곱오차이다.

• 예측성 로그가능도 훈련 목적함수를 사용하는 경우
  => $y^{(t)}$의 조건부 확률분포를 추정하도록 RNN 훈련
  => 로그 가능도 최대화

  • $y$값들의 순차열에 관한 결합분포를 일련의 단일 단계 확률 예측들로 분해하는 것도 하나의 방법!
    $P(\mathbb{Y}) = P(y^{(1)},...,y^{(\tau)}) = \prod^{\tau}_{t=1}P(y^{(t)}|y^{(t-1)},...,y^{(1)})$
    이러한 모형에 대한 음의 로그 가능도는 다음과 같이 주어진다.
    $L=\sum_{t}L^{(t)}$
    $L^{(t)} = -logP(y^{(t)}=y^{(t)}|y^{(t-1)},...,y^{(1)})$

그래프 모델의 간선은 변수들 사이의 직접적인 의존관계를 나타낸다. 그래프 모델 중에는 통계적 효율성과 계산 효율성을 높이기 위해 강한 상호작용에 해당하지 않는 간ㅅ너들을 생략하는 것도 많다.

예를 들어, 그래프 모델에서 전체 역사의 간선들을 모두 포함하는 대신 최근 k개 노드의 간선들만 포함해야한다는 마르코프 가정을 적용하는 경우가 흔하다.

RNN을 그래프 모델로 해석하는 한 가지 방법은 RNN이 임의의 두 y값 사이의 직접적인 의존성을 표현할 수 있는 완전 그래프에 해당하는 구조를 가진 그래프 모델이라고 보는 것이다.

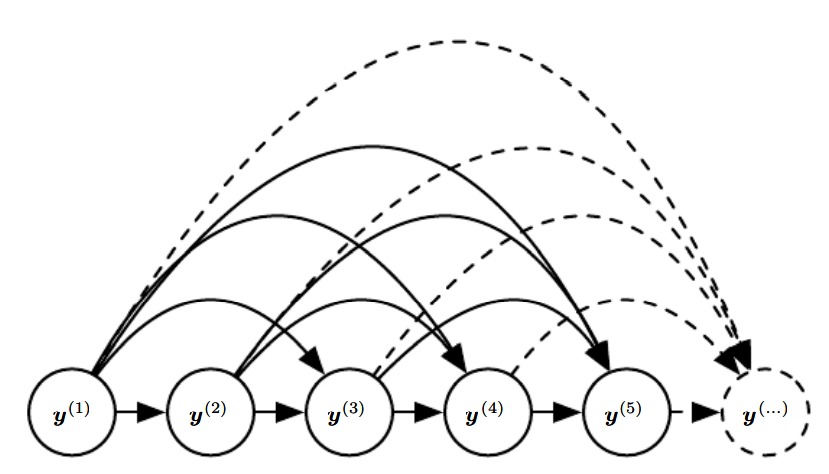
RNN을 완전 그래프로 해석하는 것은 은닉 유닛을 marginalizing해서 무시한다는 것이 내재되어 있다.

은닉 유닛 $h^{(t)}$를 확률변수들로 간주하면, RNN그래프 모형 구조를 더 흥미로운 방식으로 고찰할 수 있다.

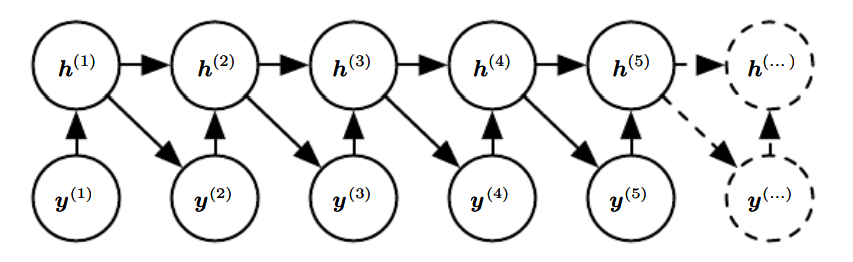
파라미터화가 얼마나 효율적인지 확인하기 쉬워진다. 순차열의 각 단계($h^{(t)}$와 $y^{(t)}$에 대한)에는 동일한 구조가 관여한다. 즉, 각 단계는 다른 단계들과 파라미터를 공유할 수 있다.

이러한 그래프 모형의 매개변수화가 효율적이긴 하지만

• 몇몇 연산의 계산 비용은 여전히 높을 수 있다.(sequence 중간에 결측치가 존재하는 경우)
• 파라미터를 최적화하기가 어려울 수 있다.
  서로 다른 시간 단계에서 같은 파라미터를 사용할 수 있다는 가정에 근거하는데, 이는 $t+1$의 변수들이 $t$에서 변수들이 주어졌을 때의조건부 확률분포가 stationary라는 가정과 동등하다.
  => 하나의 시간 단계와 그 전 시간 단계의 상호작용이 $t$에 의존하지 않는다는 것

그래프 모형으로서의 RNN에 대한 우리의 시각을 완성하려면, 그러한 모델에서 표본을 추출하는 방법도 서술해야 한다. 그냥 각 시간 단계에서 조건부 분포로부터 표본을 추출하면 된다. 하지만 문제는 RNN이 순차열의 길이를 알아낼 수 있어야 한다는 것이다.

이를 해결하는 방법은 여러 가지가 있다.

• 하나는 출력이 어떤 어휘(단어 집합)에서 뽑은 하나의 기호일 경우에, 시퀀스의 끝을 뜻하는 특별한 기호를 그 어휘에 추가
• 각 시간 단계에서 생성을 계속할 것인지 아니면 멈출 것인지를 결정하는 여분의 베르누이 출력을 모델에 도입(좀 더 일반적)
• 순차열 길이 $\tau$ 자체를 예측하는 추가적인 출력을 모델에 도입

10.2.4 Modeling Sequences Conditioned on Context with RNNs

앞에선 입력 $x$들이 없는, 확률변수 $y^{(t)}$들의 순차열에 관한 유향 그래프 모형에 해당하는 RNN을 설명했다.

이번엔 $y$변수들에 관한 결합 분포뿐만 아니라 $x$가 주어졌을 때의 $y$에 관한 조건부 분포를 표현하도록 RNN 그래프를 확장하는 것이 가능하다. 이전과 동일한 $P(y|w)$를 사용하되, $w$를 $x$의 함수로 두면 된다.

앞에선 $t=1,...,\tau$에 대한 벡터 $x^{(t)}$들의 순차열을 입력 받았다. 대신 벡터 $x$하나를 입력받는 RNN도 가능하다. $x$가 고정 크기 벡터일 때는 그냥 이를 $y$순차열을 산출하는 RNN의 여분의 입력으로 두면 된다.

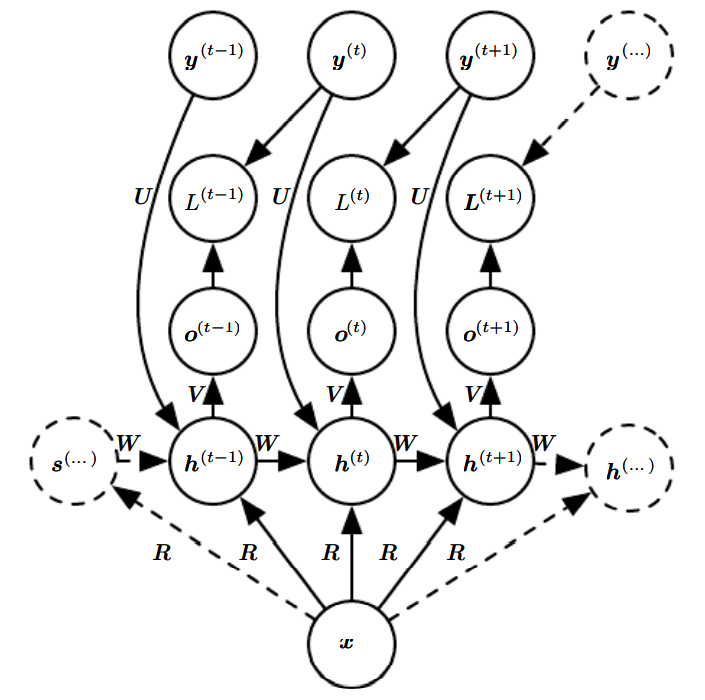
이러한 RNN은 모형이 하나의 이미지를 입력받고 그 이미지를 서술하는 문장을 출력하는 이미지 캡션 달기 같은 과제들에 적합하다.

혹은 RNN이 하나의 벡터 $x$를 입력받는 것이 아니라 벡터 $x^{(t)}$들의 순차열을 입력받을 수도 있다. 이러한 RNN은 조건부 분포 $P(y^{(1)},...,y^{(\tau)}|x^{(1)},...,x^{(\tau)})$에 해당한다. 이 때, 이 분포가 다음과 같이 인수분해 된다는 조건부 독립성 가정이 깔려있다.

만약, 아래 그림처럼 시간 $t$에서의 출력에서 시간 $t+1$에서의 은닉 유닛으로의 연결을 신경망에 추가하면 그러한 조건부 독립성 가능을 제거할 수 있다.

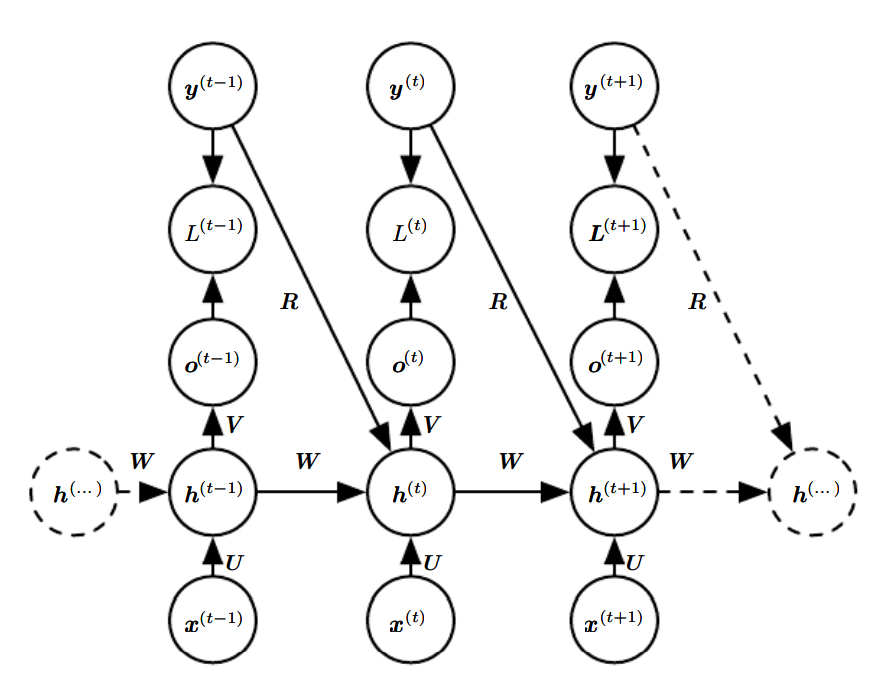
한 순차열이 주어졌을 때의 다른 한 순차열의 분포를 표현하는 이런 종류의 모형에도 제약이 하나 존재한다. 이는 10.4에서 후술하겠다.

10.3 Bidirectional RNNs

지금까지 살펴본 모든 순환 신경망에는 "인과"구조가 존재한다.
= 시간 $t$에서의 상태가 오직 과거의 $x^{(1)},...,x^{(t-1)}$과 현재 입력 $x^{(t)}$에 있는 정보만 포착한다는 것

하지만 여러 응용에서는 신경망이 출력할 예측값 $y^{(t)}$가 입력 순차열 전체에 의존할 수도 있다. 이런 필요성을 충족하기 위해 고안된 것이 양방향 순환 신경망이다. 양방향 순환 신경망은 필기 인식, 음성 인식, 생물 정보학에서 대단한 성과를 이뤘다.

양방향 RNN은 시간순 RNN과 역시간순 RNN을 결합한 것이다. $h^{(t)}$는 시간순 RNN의 상태이고, $g^{(t)}$는 역시간순 RNN의 상태이다. 이러한 구조 덕에 출력 단위 $o^{(t)}$들은 과거와 미래 모두에 의존하는, 하지만 $t$근처의 입력값들에 가장 민감하게 반응하는 표현을 계산할 수 있다.

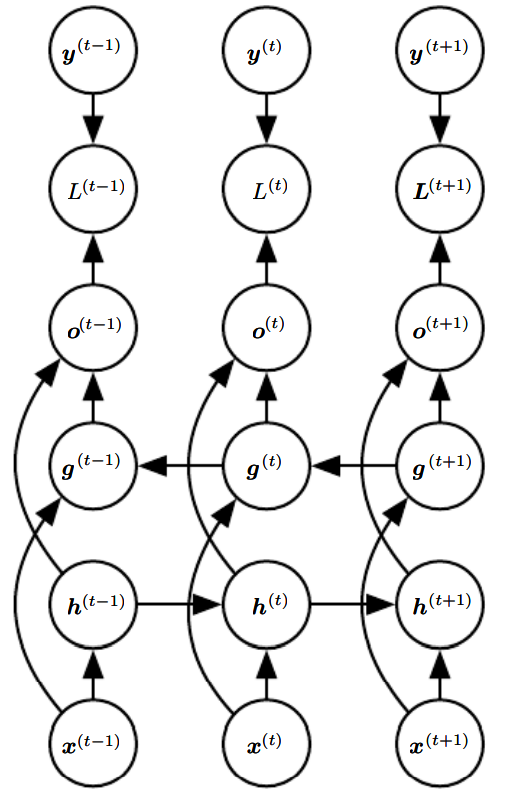
이를 2차원 입력으로 확장하면, 상하좌우 방향 각각 하나씩 총 네 개의 부분 RNN이 필요하다. 이 경우 2차원 격자의 각 점 $(i,j)$에서 출력 $O_{(i,j)}$는 주로 국소 정보를 포착하되, 좀 더 멀리 떨어진 입력들도 고려하는 표현을 계산할 수 있다.

이미지에 대한 RNN은 대체로 계산 비용이 높지만, 같은 특징 지도 안에 있는 특징들 사이의 장거리 잠재적 상호작용들을 잡아낼 수 있다는 장점이 있다.

10.4 Encoder-Decoder Sequence-to-Sequence Architectures

이번 챕터에서는 입력 순차열과는 길이가 다를 수도 있는 출력 순차열을 산출하도록 RNN을 훈련하는 방법을 살펴보자.
이러한 RNN은 음성 인석, 기계 번역, 질문 응답 등 훈련 집합의 입력 순차열들과 출력 순차열들의 길이가 다를 때가 많은 여러 응용에 유용하다.

RNN의 입력 => 문맥(context)라 부른다.
이번 챕터에서 다루는 RNN의 목표는 주어진 문맥 C의 한 표현을 산출하는 것이다. 문맥 C는 입력 순차열 $X=(x^{(1)},...,x^{(n_{x})})$를 요약하는 하나의 벡터일 수도 있고, 이러한 벡터들의 순차열일 수도 있다.

이러한 아키텍처의 동작 원리는 간단하다.
1) reader 또는 input RNN이라고 부르는 encoder RNN은 입력 순차열을 처리한다. 이 파트에서는 하나의 문맥 C를 산출하는데, 보통의 경우 문맥은 encoder의 마지막 은낙 상태의 간단한 함수이다.
2) writer 또는 output RNN이라고 불리는 decoder RNN은 고정 길이 벡터를 조건으로 하여 출력 순차열 $Y=(y^{(1)},...,y^{(n_{y})})$을 산출한다. 여기서 중요한 점은 이전과는 달리 입력 순차열의 길이와 출력 순차열의 길이가 다를 수 있다는 것이다.

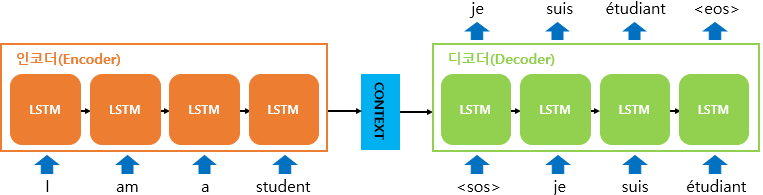
Sequence-to-Sequence에서는 두 RNN을 함께 학습하는데, 학습의 목적은 학습 데이터셋의 순차열 $x$과 $y$의 모든 쌍에 대한
$logP(y^{(1)},...,y^{(n_{y})}|x^{(1)},...,x^{(n_x)})$의 평균을 최대화하는 것이다. 일반적으로 encoder RNN의 최종 상태 $h_{n_{x}}$는 입력 순차열을 표현하는 문맥 $C$로 쓰인다. 이 문맥 $C$가 decoder RNN의 입력이다.

문맥 $C$가 하나의 벡터일 때 decoder RNN은 벡터 대 순차열 RNN 벡터 대 순차열 RNN이 입력을 받는 방식은 1)RNN의 초기 상태로 사용 2) 입력을 각 시간 단계에서의 은닉 단위들에 연결 혹은 이 둘을 결합해서 사용할 수도 있다.

하지만 이러한 구조의 한 가지 확실한 한계는 encoder가 출력한 문맥 $C$의 차원이 너무 낮으면 긴 순차열을 제대로 요약하지 못한다. 이를 해결하기 위해 $C$를 고정 크기가 아닌 가변 길이 순차열로 두라고 제안했고, $C$의 요소들을 출력 순차열의 요소들과 연관시켜 학습하는 attention mechanism에 대해 소개한다.

10.5 Deep Recurrent Networks

대부분의 RNN이 수행하는 계산은 매개변수들을 크게 세 블록으로 나누고 각각을 적절한 방식으로 변환한다.
1. 입력->은닉
2. 이전 은닉->다음 은닉
3. 은닉->출력

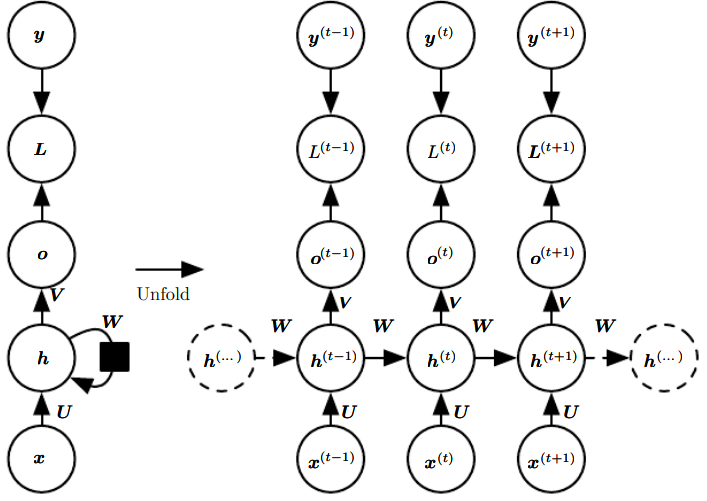
이 그림에서 U가 1번, W가 2번 V가 3번 계산에 해당한다. 신경망을 펼쳤을 때, 각 블록은 하나의 얕은 변환에 대응된다. '얕은'변환은 MLP의 층 하나로 표현할 수 있는 변환을 말한다.

하지만 신경망을 깊게 만들면 이득이지 않을까? 물론 실제로 그럴 가능성이 크다. 다음 그림은 RNN을 깊게 만드는 여러 가지 방법을 보여주고 있다.

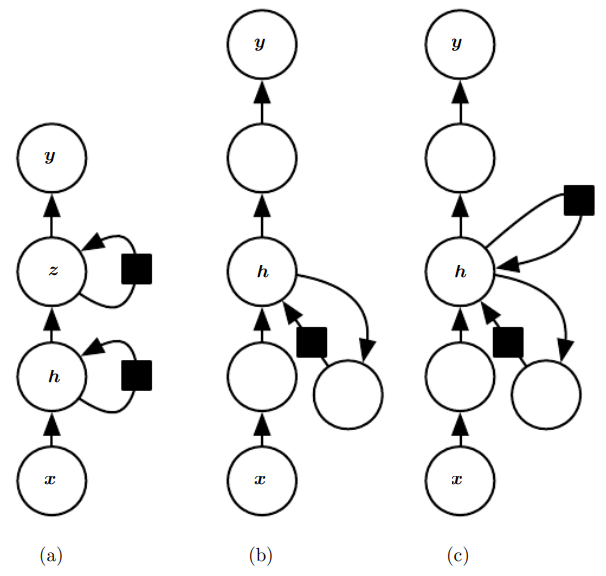
(a) : RNN의 상태를 여러 층으로 분해하면 큰 이득이 생긴다는 것을 보여준다. 여기서 아래쪽 층은 원본 입력을 은닉 상태의 상위 수준들에 좀 더 적합한 표현으로 변형하는 역할을 한다.
(b): input-to-hidden,hidden-to-hidden and hidden-to-output part사이에 MLP 따위를 추가
(c) : b의 path-lengthening effect을 완화한 예제 - skip connections in the hidden-to-hidden path

10.6 Recursive Neural Networks

재귀 신경망은 순환 신경망의 또 다른 일반화에 해당한다. RNN의 계산 그래프는 사슬 형태이지만 재귀 신경망의 계산 그래프는 깊은 트리 형태이다.

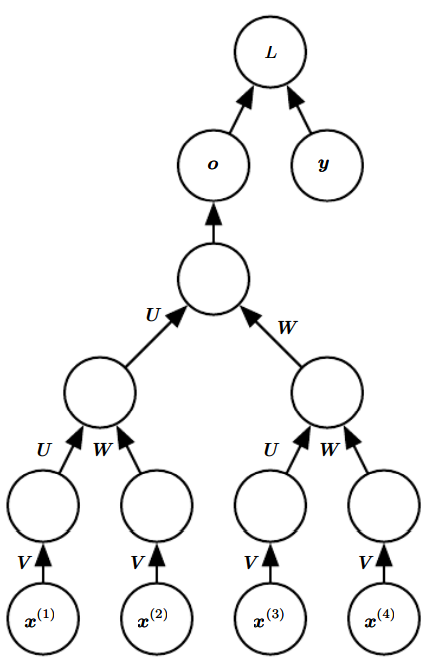
재귀 신경망은 자료구조를 신경망의 입력으로 삼아서 처리하는 응용 분야와 자연어 처리, 그리고 컴퓨터 시각에 성공적으로 적용되었다.

순환 신경망과 비교할 때 확실한 장점은

• 순차열의 길이가 $\tau$라고 할 때 순환 신경망의 깊이는 $\tau$이지만 재귀 신경망의 깊이는 $O(log\tau)$밖에 안된다는 것
  ==> 장기 의존 관계를 다루는 데 도움.
  확실한 난제는
• 트리의 구조를 어떻게 잡을 것이냐
  • 한 가지 방법은 자료에 의존하지 않는 트리 구조 (balanced binary tree) 사용
  • 하지만 외부 요인에 근거해 적절한 트리 구조를 선택하는 것이 바람직할 수 도 있음
    ex) 자연어 문장을 처리할 때는 자연어 parser가 문장을 분석해서 산출한 parse tree의 구조를 그대로 사용해도 된다.
  • 물론 가장 이상적인 방법은 학습 모형 자체가 임의의 주어진 입력에 적합한 트리 구조를 발견, 추론하는 것

10.7 The Challenge of Long-Term Dependencies

장기 의존성(long-term dependency)의 학습에서 나타나는 수학적 문제점 하나는 여러 단계에 걸쳐 전파되는 기울기들이 소멸하거나 폭발하는 경향이 있다는 것

순환 신경망은 같은 함수를 시간 단계당 한 번씩 어러 번 합성한다. 이러한 다수의 합성 때문에 신경망이 극도로 비선형적인 방식으로 행동할 수 있다.

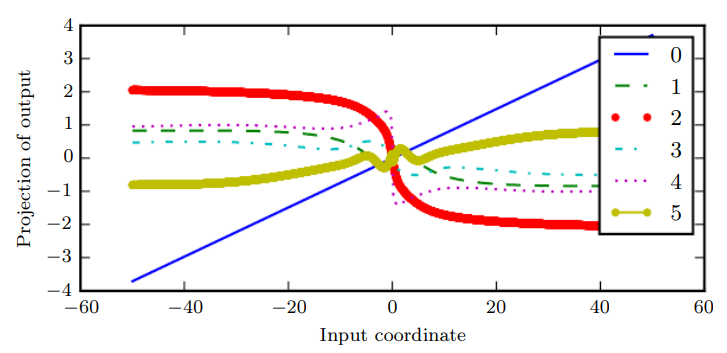
이 그래프에서 y축은 100차원 은닉 상태를 선형 투영을 통해 1차원으로 축약한 것이고, x축은 100차원 공간의 한 무작위 방향을 기준으로 한 초기 상태의 좌표이다. 이 그래프를 고차원 함수의 한 선형 단면으로 보아도 좋다. 그래프는 각 시간 단계 이후의, 다른 말로 하면 각 합성 횟수에서의 전이 함수 값을 보여준다.❓
(여기서 범례가 의미하는게, 합성 횟수! == 비선형성이 얼마나 더 가해졌는가!)

순환 신경망이 사용하는 함수 합성은 행렬 곱셈과 비슷하다.

을 비선형 활성화 함수가 없고 입력 $x$도 없는 아주 단순한 순환 신경망으로 간주할 수 있다. 이러한 점화식은 본질적으로 하나의 거듭제곱법을 나타낸다. 이를 다음과 같이 좀 더 간단한 공식으로 정리할 수 있다.

그리고 만약 $W$의 고윳값 분해가 다음과 같은 형태이면(여기서 Q는 직교 행렬) 이 점화식을 다음과 같이 좀 더 간단하게 쓸 수 있다.

고윳값들이 $t$를 지수로 해서 거듭제곱되므로, 크기가 1보다 작은 고윳값은 0으로 소멸하고 크기가 1보다 큰 고윳값은 폭발한다. 즉, $h^{(0)}$의 성분 중 가장 큰 고유벡터와 방향이 맞지 않는 모든 성분은 사라진다.

이 문제는 순환 신경망에서 두드러진다. 간단하게 설명하기 위해 백터 대신 스칼라를 사용한다고 하면,

• 순환 신경망은 가중치 $w$를 그 자신과 여러 번 곱할 것이고, 그 거듭제곱 $w^t$은 $w$의 크기에 따라 소멸하거나 폭발한다.
• 비순환 신경망에서는 초시 강태가 1이라고 할 때, 시간 $t$에서의 상태는 곱 $\prod_t w^{(t)}$이다. 여기서 $w^{(t)}$은 서로 독립적으로 평균이 0 이고 분산이 $v$인 분포에 따라 무작위로 생성한다 가정 => 곱의 분산은 $O(v^n)$이다.
  이 때 분산이 $v^*$이길 원한다고 하면, $v=\sqrt[n]{v^{*}}$인 가중치를 선택하면 됨.
  ==> 아주 깊은 순방향 신경망에서 비례 계수를 세심하게 선택하면 기울기가 소실되거나 폭발하는 문제를 피할 수 있다.

그냥 기울기들이 소멸하거나 폭발하지 않는 영역으로 매개변수들을 한정하면 RNN의 기울기 소멸 및 폭발 문제를 해결할 수 있지 않을까? => 불행히 작은 섭동에 대해 안정적이도록 기억들을 저장하려면 RNN은 반드시 기울기들이 소멸하는 매개변수 영역으로 들어가야 함.
==> 모델이 장기 의존성을 표현할 수 있다면, 장기 상호작용의 기울기는 단기보다 지수적으로 작다. 즉, 장기 의존성을 배우는 것이 불가능하다는 것이 아니라 학습이 오래걸린다는 것
(학습이 오래걸린다는 것은 장기 의존성에 대한 작은 신호가 단기 의존성에서 발생하는 아주 작은 변동에 가려지는 경향이 있기 때문)

실제로 포착해야 할 의존성들의 기간을 늘릴수록 기울기 기반 최적화가 점점 어려워져서, 순차열의 길이가 10이나 20정도만 되어도 전통적인 RNN을 확률적 경사 하강법으로 훈련해서 학습에 성공할 확률이 급격히 0에 접근한다.

10.8 Echo State Networks

feedforward network를 가장 간단하게 구성하는 방법은 raw input에 임의의 가중치를 곱해 hidden unit으로 변환하고 다음에 이를 output으로 사상하는 선형 함수를 학습시키는 것이다.
==> 이렇게 하면 input의 표현을 확장시켜 output이랑 더 잘 맵핑될 수 있음.
===> 이 아이디어를 RNN에 적용한 게 ESN!

$h^{(t-1)}$에서 $h^{t}$로의 순환 가중치 사상(은닉->은닉)과 $x^{(t)}$에서 $h^{(t)}$로의 입력 가중치 사상(입력->은닉)은 순환 신경망에서 학습하기 가장 어려운 매개변수들에 속한다. 그러한 어려움을 해소하기 위해 제안된 방법 중 하나가 순환 은닉 단위들이 과거 입력들의 역사를 제대로 포착할 수 있도록 1) 순환 가중치들을 설정하되, 2) 신경망이 출력 가중치들만 배우게 하는 것이다.

이러한 방식을 바탕으로 반향 상태 신경망(echo state network, ESN)과 액체 상태 기계(liquid state machine)가 독립적으로 제시 되었다. 둘은 거의 비슷하지만 ESN은 연속값 은닉 단위들을 사용하고, 후자는 스파이킹 뉴런(이진 값 출력)을 사용한다.

이 둘을 통칭해서 저장소 컴퓨팅(reservoir computing)이라고 부른다. 저장소 컴퓨팅은 은닉 단위들이 입력 역사의 서로 다른 측면들을 포착할 수 있는 시간적 특징들의 저장소를 형성한다.

저장소 RNN은 임의의 길이의 순차열(시간 $t$까지의 입력 역사)을 고정 길이 벡터($h^{(t)}$)로 사상하고, 이러한 벡터에 선형 예측기를 적용함으로써 주어진 문제를 풀 수 있다. 그러면 학습 판정기준은 그냥 출력 가중치들의 함수로서의 볼록함수로 두면 된다.

예를 들어, 신경망의 출력이 은닉 단위들에서 출력 목표값들로의 선형회귀이고, 학습 판정 기준이 평균제곱오차이면, 이는 볼록함수이므로 간단한 학습 알고리즘으로 풀 수 있다.

여기서 드는 의문은 그러면 순환 신경망 상태가 풍부한 역사를 표현할 수 있도록 입력 가중치들과 순환 가중치들을 설정하는 방법은 무엇인가!이다.

여기서 제시한 답은, 순환 신경망을 하나의 동역학계로 간주해서, 입력 가중치들과 순환 가중치들을 그러한 동역학계가 안정성의 가장자리에 놓이게 하는 값들로 설정하는 것이다.

원래는 상태 전이 함수의 야코비 행렬의 고윳값들을 1에 가깝게 두는 것이었다. 여기서 중요한 부분은 야코비 행렬 $J^{(t)} =\frac{\partial s^{(t)}}{\partial s^{(t-1)}}$의 고윳값 스펙트럼이다. 특히 $J^{(t)}$의 스펙트럼 반경(spectral radius)가 중요한데, 이 스펙트럼 반경은 절댓값이 가장 큰 고유값의 절댓값으로 정의된다.

스펙트럼 반경의 효과를 이해하기 위해, $t$에 따라 변하지 않는 야코비 행렬 $J$를 가진 신경망의 역전파를 생각해보자.

• $v$가 $J$의 한 고유벡터이고, $\lambda$는 해당 고윳값이라고 할 때, 초기 기울기 벡터 $g$로 시작해서 역전파를 n단계 시행하면 $J^ng$가 된다.
• 이번엔 $g$르 섭동(pertubation)한 버전으로 역전파 한다고 하면, n단계 후의 기울기는 $J^n(g+\delta v)$이다.

이 둘을 비교해 보면, $g$로 시작하는 역전파와 $g+\delta v$로 시작하는 역전파는 $n$단계 후에 $\delta J^n v$만큼 다르다. $J$의 단위 고유벡터 하나를 $v$(해당 고윳값은 $\lambda$인)로 두면, 두 역전파 방법은 $\delta|\lambda|^n$만큼 떨어져 있다. $v$가 $|\lambda|$의 가장 큰 값에 해당한다면, 초기 섭동 크기 $\delta$로 얻을 수 있는 가장 넓은 분리 거리가 나온다.
즉, $|\lambda|>1$일때는 두 방법의 거리가 지수적으로 커지고, 반대 경우에는 지수적으로 작아진다.

물론 이는 모든 시간 단계에서 야코비 행렬이 동일하다고 가정한 것이다(== 비선형성이 없는 순환 신경망)

비선형성이 존재하는 경우에는 여러 시간 다계 후에 비선형성의 미분이 0에 접근하므로 큰 스펙트럼 반경 때문에 생기는 폭발이 방지된다. 실제로, ESN에 관한 최근 문헌은 대부분은 단위원보다 훨씬 큰 스펙트럼 반경을 사용할 것을 권한다.

행렬 곱셈의 반복을 통한 역전파에 대해 이야기한 모든 것들은 위에서 정의한 $h^{(t+1)} = h^{(t)T}W$에서도 동일하게 적용된다. $W^T$가 항상 $h$를 축소할 때, 이러한 사상을 축약사상이라고 한다. 즉, 스펙트럼 반경이 1보다 작으면 $h^{(t)}$에서 $h^{(t+1)}$의 사상은 축약 사상이라고 한다. 따라서 작은 변화는 시간 단계 마다 작아지고, 상태 벡터를 유한한 정밀도(32bit integer)로 저장하면 신경망은 과거의 정보를 잊게 된다.

야코비 행렬은 $h^{(t)}$의 작은 변화가 다음 다계로 어떻게 전파되는지 말해준다. $W$나 $J$가 반드시 대칭행렬일 필요는 없다(단, 정방 행렬이자 실수값 행렬이어야 함). 따라서 둘다 고유값과 고유벡터가 복소수일 수 있다. 허수부는 잠재적인 진동 행동에 대등된다(동일한 야코비 행렬을 반복해서 적용하는 경우).

비선형 사상의 경우 야코비 행렬이 단계마다 다를 수 있다. 하지만 초기의 작은 변동이 여러 단계 후엔 크 변동으로 바뀐다는 것은 선형과 동일하낟. 순수하게 선형인 사상과 비선형 사상의 한 가지 차이점은, tanh처럼 넓은 정의역 또는 다양한 입력값을 좁은 치역 혹은 소수의 출력값으로 줄이는 압착(squashing) 비선형 함수를 사용하면 순환 동역학이 유계가 될 수 있다는 것. 물론 순전파의 동역학이 유계여도 역전파의 동역학은 유계가 아닐 수 있음.

ESN의 전략은 단순히 가중치들의 스펙트럼 반경을 정보가 시간순으로 흐르되, tanh 같은 비선형성이 포화해서 생기는 안정화 효과 덕분에 폭발이 일어나지 않게 하는 어떤 값으로 고정하는 것
❓이게 그냥 RNN이랑 무슨 차이야..

좀 더 최근에는 ESN의 가중치들을 설정하는 데 쓰이는 기법들을 전체 학습이 가능한 순환 신경망의 가중치들을 초기화하는 데 사용함으로써 장기 의존성들의 학습을 개선하는 것이 가능하다는 점이 밝혀졌다.

추가 자료
ESN의 장점

• ESN은 단지 선형 모델만 fit하면 되니까 학습이 매우 빠르게 될 수 있다.
• 가중치를 아주 민감하게 초기화하는 것이 매우 중요하다.
• 1차원의 시계열 모델링을 잘할 수 있다.(단 전처리된 음성과 같은 다차원 데이터는 잘 안 됨.)

ESN의 단점

• hidden->hidden 가중치를 학습하는 RNN보다 hidden unit이 많이 필요할 수 있음.
• ESN을 통해 가중치가 초기화 된다면 RNN은 매우 효율적으로 학습될 수 있다고 함.
  (rmsprop와 momentum 사용)

스터디 후 추가
두 모델의 차이점 :

• Echo state network : Continuous-valued hidden units사용
• Liquid state machine : Spiking neuron 사용 (binary output, 0 or 1)

두 모델의 공통점 : 대체로 비슷, Reservoir computing(저장소 컴퓨팅)라 통칭

10.9 Leaky Units and Other Strategies for Multiple Time Scales

장기 의존성을 처리하는 한 가지 방법은 모델이 여러 시간 축척(time scale)들에서 작동하도록 설계하는 것. 즉, 모델의 일부는 세밀한(fine-grained) 시간 축척에서 작동해서 작은 것들을 처리하고, 또 다른 일부는 드문 드문한(coarse) 시간 축척 척도에서 작동해 먼 미래의 정보가 현재로 좀 더 효율적으로 전달되게 하는 것이다. 이러한 것을 지원하는 모델을 구축하는 전략은 1) skip connection을 모델에 추가해 일부 시간 단계들을 건너뛰거나, 2) 서로 다른 시간 상수를 가진 leaky unit들로 여러 신호를 통합하거나, 3) 조밀한 시간 축척에 쓰이는 연결의 일부를 제거(Remove connection)하는 등의 전략이 있다.

10.9.1 Adding Skip Connections through Time

한 논문은 시간 지연이 $d$인 순환 연결을 이용해서 그러한 문제점을 완화하는 방법을 제시한다.
이 방법을 적용하면,

• 기울기들은 $\tau$가 아니라 $\frac{\tau}{d}$의 함수로 지수적으로 소멸
• 한 순환 신경망에 시간 지연 연결들과 단일 시간 단계 연결들이 공존하므로, 기울기들이 $\tau$에 따라 지수적으로 폭발할 여지는 여전히 남아 있음.
• 더 긴 의존성을 잡아낼 수 있지만 안되는 애들도 있음.

10.9.2 Leaky Units and Spectrum of Different Time Scales

어떤 값 $v^{(t)}$이 이동 평균 $\mu^{(t)}$를 $\mu^{(t)} \leftarrow \alpha\mu^{(t-1)} + (1-\alpha)v^{(t)}$갱신을 반복해 누적한다고 하자. 이때 파라미터 $\alpha$가 바로 $\mu^{(t-1)}$에서 $\mu^{(t)}$로의 선형 자기 연결의 예이다. $\alpha$가 1에 가까울 수록 이동 평균은 먼 과거의 정보를 기억하고, 0에 가까울 수록 과거의 정보는 빠르게 폐기 된다.

선형 자기 연결이 있는 은닉 유닛들은 이런 이동 평균과 비슷하게 행동한다. 이런 은닉 유닛들을 leaky unit라고 한다.

leaky unit에 쓰이는 시간 상수들을 설정하는 전략은 크게 두 가지이다. 1) 고정된 값을 직접 지정 2) 시간 상수를 자유 매개변수로 두어 신경망이 학습하게 하는 것.

10.9.3 Removing Connections

이 방식은 길이가 1인 연결을 능동적으로 제거하고 더 긴 연결을 삽입한다는 점에서 adding skip connection과 다르다. 이러한 방식으로 수정된 단위들을 간격이 더 긴 시간 축척에서 작동한다. 반면, skip connection은 간선을 추가한다. 이러한 새 연결이 추가된 유닛은 긴 시간 축척에서 작동하는 방법을 배울 수도 있지만, 그냥 자신의 다른 단기 연결들에 집중할 수 도 있다.

여러 순환 유닛 그룹들이 서로 다른 시간 축척들에서 작동하도록 강제하는 방법은 여러가지이다.
1. leaky unit들로 이뤄진 순환 유닛 그룹들을 각자 서로 다른 고정된 시간 축척과 연관시키는 것
2. 유닛 그룹들을 각자 다른 빈도로 갱신하는 것

10.10 The Long Short-Term Memory and Other gated RNNs

leaky unit을 사용하는 RNN처럼 gated RNN은 미분들이 소멸하지도, 폭발하지도 않는 시간 경로를 만들어 낸다는 착안에 기초한다. leaky unit에서는 연결 가중치들을 직접 지정하거나 매개변수로 두어 학습하게 했지만, gated RNN은 이를 가중치들이 시간 단계마다 변할 수 있는 모델로 일반화한다.

leaky unit 방식에서는 신경망이 정보를 오랜 기간에 걸쳐 누적할 수 있다. 하지만 이러한 정보가 사용된 후에는 신경망이 기존 상태를 잊어버리는 것이 유용할 수 있다. 이렇게 기존 상태를 제거하고 싶을 때 이를 명시적으로 지정하기 보단, 그 시점을 결정하는 방법을 신경망이 배우게 하는 것이 바람직하다. ==> gated RNN

10.10.1 LSTM

자기 연결 루프(self-loop)의 가중치를 조건화, 즉, 다른 어떤 은닉 유닛이 '게이트'역할을 해서 가중치를 제어하게 하면, 시간의 축적이 다이나믹하게 변할 수 있다(무언가는 버리고 무언가는 남기는 식으로 좀 더 다양하게 과거 정보들을 저장할 수 있음).

아래 그림은 LSTM의 구조도이다. 이는 그 밑의 수식으로 순전파를 정의할 수 있다. LSTM은 단순히 입력을 받아 affine 변환 후, 비선형성을 부여하는 것이 아니라 'LSTM 세포'들로 구성된다. LSTM 세포들은 RNN의 바깥쪽 순환 뿐만 아니라 내부 순환(self-loop)도 있다.

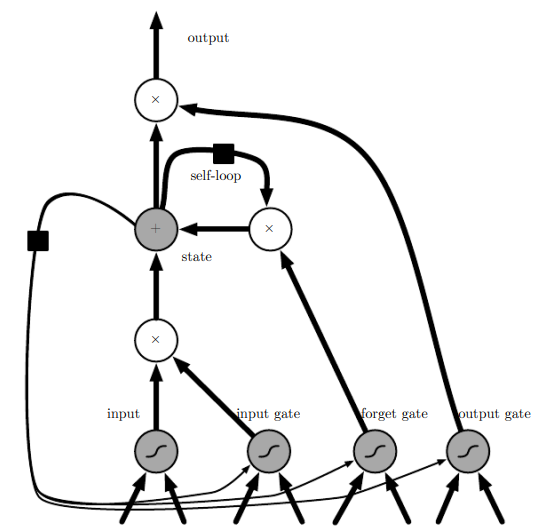
각 세포에는 정보의 흐름을 제어하는 게이트 시스템이 존재한다. 한 세포의 가장 중요한 구성요소는 상태 유닛 $s_{i}^{(t)}$인데, linear self-loop가 존재한다. leaky unit과 다른 점은, self loop 가중치를 망각 게이트(forget gate)가 제어한다는 것이다. 시간 단계 $t$에서의 세포 $i$에 대한 망각 게이트를 $f^{(t)}_{i}$로 표기하면, 구체적인 수식은 다음과 같다.

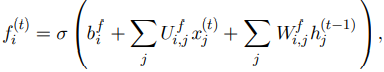
• $x^{(t)}$ : 현재 입력 벡터
• $h^{(t)}$ : 모든 LSTM 세포의 출력을 담은 현재 은닉 층 벡터
• $b^f$ : 망각 게이트의 편향
• $U^f$ : 입력 가중치
• $W^f$ : 순환 가중치(은닉 층에 대한 가중치)

LSTM 세포의 내부 상태는 조건부 self loop 가중치 $f_{i}^{(t)}$에 따라 다음과 같이 갱신된다.

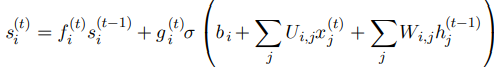
• $b$, $U$, $W$ : LSTM세포의 편향, 입력 가중치, 순환 가중치

외부 입력 게이트($g_t^{(t)}$)는 다음과 같이 쓸 수 있다.

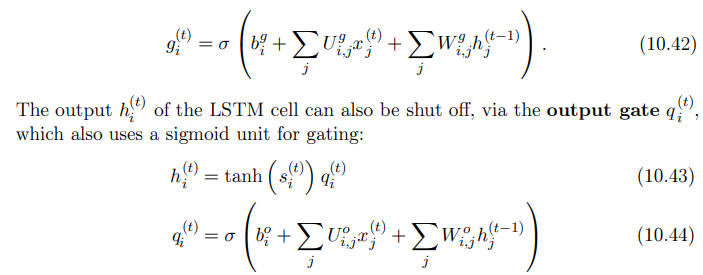
종합하면,

• 현재 x와 직전 단계의 h를 써서 tanh(상태유닛)*출력 게이트가 LSTM셀의 출력 h가 됨.
• 각각의 망각 게이트(f), 외부 입력 게이트(g), 출력 게이트(q)는 x와 h에 각각 게이트의 가중치를 곱하고, 편향을 더해 계산 됨.
• 상태 유닛은 직전 상태 유닛*망각 게이트 + (LSTM 세포 자체의 가중치, 편향)*외부 입력 게이트으로 계산됨.

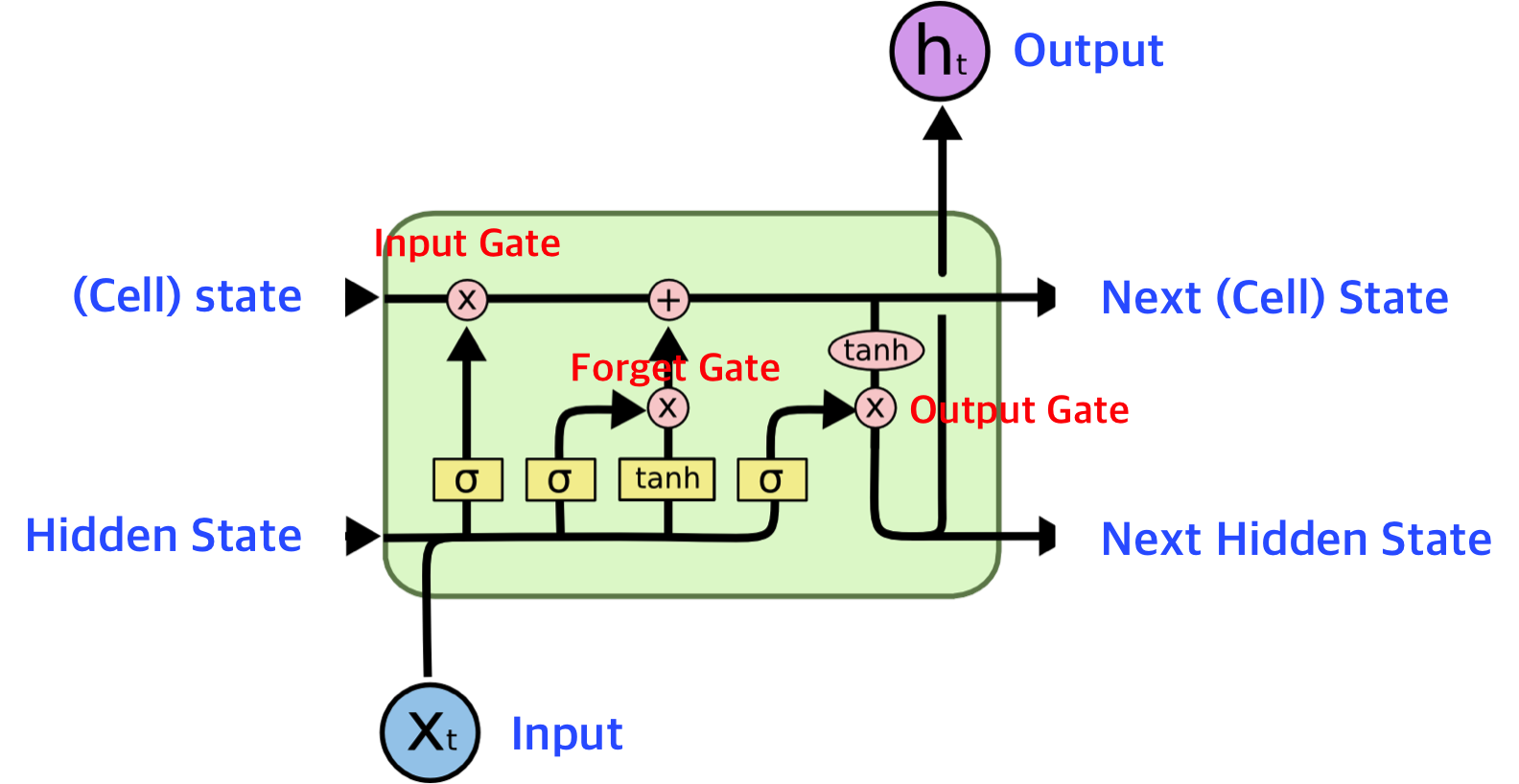
LSTM 순환 신경망이 보통의 순환 신경망보다 장기 의존성을 더 수월하게 학습한다는 점이 밝혀졌다.

10.10.2 Other Gated RNNs

GRU(gated recurrent unit)와 LSTM의 차이는 하나의 게이트 유닛이 상태 유닛 갱신 여부와 망각 인자를 동시에 제어한다는 것이다. 이를 수식으로 표현하면 다음과 같다.

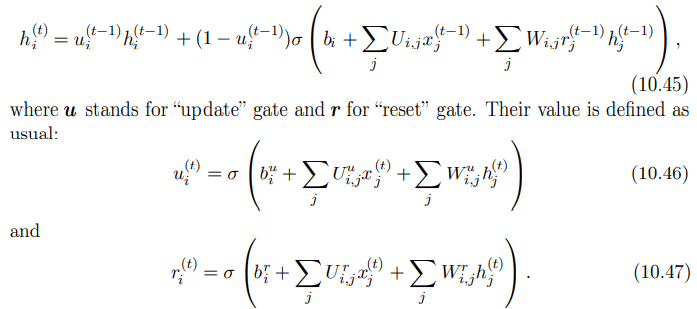
u(update)가 직전 게이트를 얼마나 반영하고, 현재 입력값을 얼마나 반영할지를 결정한다. r(reset)은 현재 입력값에 h를 얼마나 반영할지를 나타낸다.

갱신 게이트와 재설정 게이트는 상태 벡터의 성분들을 각자 독립적으로 무시할 수 있다.

• 갱신 게이트는 특정 차원의 성분을 복사하거나, 완전히 무시하거나, 새 '목표 상태'값으로 대체 할 수 있다.
• 재설정 게이트는 다음 목표 상태의 계산에 쓰일 상태 성분들을 제어, 과거 상태와 현재 상태의 관계에 비선형적으로 영향을 끼친다.

이 외에도 여러 변형이 있었으나 다양한 과제들에 대해 LSTM과 GRU보다 확실히 더 나은 성과를 내는 변형은 없었다.

다른 논문에 따르면 필수 구성요소로 망각 게이트를 꼽았고, LSTM 망각 게이트에 1의 편향을 더하면 LSTM이 조사된 아키텍처 변형 중 최고의 것과 비등한 성능을 낸다는 것을 알아냈다.

10.11 Optimization for Long-Term Dependencies

앞에서 RNN을 여러 시간 단계 동안 최적화할 때 발생하는 가중치 소멸 및 폭발 문제를 설명했다. 이와 관련해 타 논문은 흥미로운 아이디어를 제시했는데, 1차 미분이 소멸할 때 2차 미분도 함꼐 소멸할 수 있다는 것이다.

이를 쉽게 이해하는 방법은 1차 미분을 2차 미분으로 나눈 값을 생각해보는 것이다. 만약 2차 미분이 1차 미분과 비슷한 속도로 감소하면, 이 값은 별로 변하지 않을 것이다. 하지만 그러한 2차 최적화 방법들은 계산 비용이 높고, 큰 미니배치가 필요하며 안장점으로 끌려가기가 쉽다.

물론 다른 2차 최적화 방법들로도 좋은 성과를 낼 가능성이 있다. 네스트로프 운동량과 같은 단순한 방법 + 섬세한 초기값 설정이 비슷한 결과를 낼 수 있다. 하지만 이러한 방법들 보다 확률적 경사 하강법(SGD)를 사용하는 것이 더 낫다.

결론적으로, 최적화하기 쉬운 모형을 설계하는 것이 좀 더 강력한 최적화 알고리즘을 설계하는 것보다 훨씬 쉬울 때가 많다.

10.11.1 Clipping Gradients

고도로 비선형적인 함수들(ex. 여러 시간 단계를 거치는 RNN)은 그 미분의 크기가 아주 커지거나 아주 작아지는 경향이 있다. 이 경우 경사 하강법의 파라미터 갱신 과정에서 파라미터들이 목적함수가 좀 더 커지는 먼 영역으로 확 이동할 수 있다. 그러면, 지금까지의 성과가 대부분 사라진다. 따라서 한 경사 하강 단계의 갱신은 비용이 다시 상승하지 않을 정도로 작아야 한다.

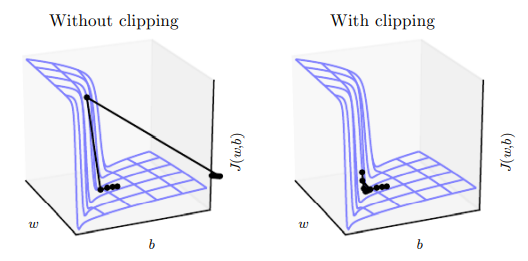
실무자들이 수년간 사용한 간단한 방법은 기울기 절단(gradient clipping)이다. 기울기를 절단 또는 한정하는 방법은 여러가지지만, 책에서 소개하는 방법은 파라미터 갱신 직전에 기울기 $g$의 크기 $||g||$를 절단하는 방법이다.

이 방법은 모든 파라미터의 기울기를 하나의 비례계수로 재정규화하므로, 각 단계가 여전히 기울기 방향을 벗어나지 않는다는 장점이 있다. 즉, 기울기가 폭발해도 파라미터들이 해에서 너무 멀어지지 않게 하는 효과를 낸다.

Clipping graident 방법 3가지가 소개됨, 성능은 비슷

• Clip the parameter gradient from a minibatch element-wise just before the parameter update
• Clip the norm $||g||$ of the gradient g just before the parameter update
• Taking a random step when the graident magnitude is above a threshold

=> 즉, Gradient descent with "heuristic bias"(때떄로 진 기울기와 좀 다른 값)이 유용하다는 것이 경험적으로 입증됨.

10.11.2 Regularizing to Encourage Information Flow

기울기 절단은 기울기의 폭발을 다루는 데는 도움이 되지만, 기울기의 소멸을 다루는 데는 도움이 되지 않는다. 기울기 소멸 문제를 해소하고 장기 의존성을 좀 더 잘 포착하는 하나의 방법으로 역전파 과정에서 기울기 벡터 $\nabla_{h^{(t)}} L$의 크기가 일정하게 유지되도록 하는 방법이 있다. 이를 수식으로 표현하면 이 값이

아래 값보다 작아지지 않게 만드는 것이다.

이를 위해 다음과 같은 정규화 항을 제안했다.

이를 clipping gradient와 같이 적용하면 RNN이 훨씬 더 긴 의존성들을 학습할 수 있다. 하지만 자료에 중복이 많은 과제(언어 모델)에 대해선 LSTM에 비해 덜 효과적이다!