글쓴이의 당부

NeRF : Representing Scenes as Neural Radiance Fields for View Synthesis 논문을 공부용으로 번역한 글입니다. 고작 학부 재학생 수준의 제멋대로인 번역으로 가독성은 별로 좋지 않습니다. 5절까지 번역되어 있습니다. 웬만하면 원문을 읽으시거나 유튜브에서 관련 동영상을 찾아보시길 권장드립니다.

추천 영상 : PR-302: NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

Abstract

우리는 입력 시점의 sparse set을 이용하는 continuous volumetric scene function을 학습하여, 복잡한 장면에 대한 새 시점을 합성하는 태스크(synthesizing novel niew)에 SOTA를 달성하는 새 방법을 제시한다. 우리의 알고리즘은 단일한 5D 좌표를 입력으로 이용하고, 공간상 한 지점에서의 volume density와 view-dependent emitted radiance(역자 - 밀도와 빛에 따라 달라지는 빛)을 출력하는 fully connected network(non-convolutional)를 이용해 장면을 표현한다. 우리는 카메라 빛을 따라서 5D 좌표의 출력값을 이용해 시점을 합성하고(synthesize views), 전통적인 volume rendering 기법을 이용해 색과 밀도를 이미지로 사영(project)한다. Volume rendering 기법은 미분 가능하므로, 학습할 유일한 입력은 카메라 위치가 알려진 이미지들의 집합이다. 우리는 photorealistic novel view of scene 렌더링하기 위해 어떻게 NeRF(neural radiance field)를 최적화해야 하는지를 설명한다. 그리고 neural rendering과 시점 합성 태스크에서 이전의 결과들을 뛰어넘는 성능을 보여줌을 입증한다. 시점 합성의 결과물은 비디오를 통해서 제일 잘 확인할 수 있으므로, 설득력 있는 비교를 위해서 보충 비디오를 보는 것을 독자분들께 촉구하는 바이다.

키워드 : scene representation, view synthesis, image-based rendering, volume rendering, 3D deep learning

1. Introduction

이 연구에서, 우리는 캡처 이미지들의 집합을 렌더링 할때의 에러를 줄이기 위해 연속적인 5D 장면 표현의 파라미터들을 직접 최적화(학습)하는 새로운 방법으로 시점 합성의 오래된 문제를 다룬다.

우리는 정적인 장면을 (1)공간상의 점 $(x,y,z)$마다 방향 $(\theta, \phi)$로 방출하는 빛, (2) 각 점 $(x,y,z)$마다 빛이 얼마나 통과할 것인지를 결정하는 불투명처럼 행동하는 밀도(density)를 출력으로 하는 연속적인 5D 함수로 표현한다. 우리의 방법은 컨볼루션 레이어 없이 오직 fully connected neural network(= multilayer perceptron, MLP)만을 이용한다. 그리고 5D 좌표 $(x,y,z,\theta,\phi)$를 이용해 밀도(single volume density)와 색(view-dependet RGB color)를 회귀(regress)함으로써 이 함수를 표현한다. 이 NeRF(neural radiance field)를 특정 시점에서 렌더링 하기 위해서 (1) 장면의 카메라 빛들을 따라가며 공간상의 3D 포인트들을 샘플링하고 (2) 이 포인트들과 대응하는 2D 시점 방향을 신경망의 입력으로 사용해 (각 포인트들의) 색과 밀도를 얻어낸 후, (3) 전통적인 volume rendering 방식을 이용해 색과 밀도를 누적하는 방식으로 2D 이미지를 만들어낸다. 이 과정 모두 미분 가능하기 때문에, 우리는 관찰한 이미지와 이에 대응되는 렌더링된 결과물의 간의 차이(에러)를 줄여나가며 모델을 최적화하는(학습하는) 과정에서 그래디언트 경사하강법을 사용할 수 있다. 다양한 시점에 걸쳐 에러를 줄여나가는 것은 결국 네트워크로 하여금 장면에 대해 일관성 있고 정답에 가까운 모델링이 가능하도록 한다. (Minimizing this error across multiple views encourages the network to predict a coherent model of the scene by assigning high volume densities and accurate colors to the locations that contain the true underlying scene content.) 그림2는 전체적인 과정을 보여주고 있다.

우리는 복잡한 장면에 대한 NeRF의 기초적인 구현체는 고해상도의 결과물을 낼 만큼 충분히 수렴하지 못하고, 카메라 빛당 요구 샘플 개수 측면에서 비효율적인 것을 확인했다. 우리는 이 문제를 5D 입력을 positional encoding으로 변환하는 방법으로 접근한다. 이는 MLP가 higher frequency function을 표현할 수 있도록 한다. 또한 우리는 hirearchial sampling을 제안한다. 이는 high-frequency scene representation을 위해 샘플링하는 과정에서 요구되는 적정 샘플의 개수를 줄이는 역할을 한다.(we propose a hierarchical sampling procedure to reduce the number of queries required to adequately sample this high-frequency scene representation.)

우리의 접근은 volumetric representation의 장점을 공유한다. 두가지 모두 실제 세계의 복잡한 모양을 표현할 수 있고, projected image를 이용한 그래디언트 기반 학습에 적합하다. 특히 복잡한 장면을 고해상도로 모델링 할 때 discretized voxel grid는 지나치게 큰 저장 공간을 요구하는데, 우리의 방법은 이를 극복할 수 있다는 점이 중요하다. 요약하자면 우리의 기술적 기여는 다음과 같다.

• 기본적인 MLP를 이용한 5D NeRF를 이용해, 복잡한 모양과 재질의 연속적인 장면을 표현하는 방법 제시
• 표준적인 RGB 이미지로부터 scene representation을 학습하기 위해 사용하는 전통적인 volume rendering 기법 기반의 미분 가능한 렌더링 방식 제시. 이는 MLP의 능력을 향상시키는 hirearchial sampling도 포함한다.
• 5D 좌표를 더 고차원의 공간으로 매핑하는 positional encoding 제시. NeRF를 high-frequency scene content를 표현할 수 있을만큼 성공적으로 학습하는 것이 가능케 함.

2. Related Work

최근의 연구 동향은 3D 공간을 signed distance와 같은 잠재적인(implicit) shape representation으로 맵핑하는 MLP를 이용하여, object와 scene을 인코딩하는 것이다. 그러나 이러한 방법들은, triangle meshes / voxel grids와 같은 이산적인(discrete) representation을 사용한 방법만큼 정교하게 현실 세계를 재현(reproduce)하는 것에는 실패했다. 이 섹션에서는 이러한 두 갈래의 연구들과 우리의 연구를 비교한다. 우리의 접근법은 복잡한 현실 세계를 렌더링하는 SOTA 모델에 사용되는 neural scene representation의 능력을 진일보시켰다.

Neural 3D shape representation

최근의 연구는 xyz 좌표를 singed distance 함수나 occupancy field로 매핑하는 DNN을 이용한, 연속적인 3D shape의 잠재 표현(implicit representation of continuous 3D shapes as level sets)를 조사했다. 그러나 이러한 모델들은 ShapeNet과 같이 합성 3D shape 데이터셋에서 얻어지는 ground truth 3D geometry에만 한정되는 문제가 있었다. 이후의 연구는 미분가능한 렌더링 함수를 이용해 이 문제를 완화했다. 이는 2D 이미지만을 이용해 신경망적 잠재 모양 표현 (neural implicit shape representation)을 최적화할 수 있도록 해주었다. Niemeyr은 표면을 3D occupancy field로 표현하고, 각 ray마다 surface intersection을 수학적인 방법으로 찾은 후에, 음함수 미분(implicit diffrentiation)을 이용해 정확한 미분값(exact derivative)를 계산하는 방법을 제시한다. 각각의 ray intersection 위치는 그 점에 대해 diffuse color를 예측하는 neural 3D texture field의 input이다. Sitzmann은 각각의 연속적인 3D 좌표에서 단순히 feature vector와 RGB 컬러를 출력하는 덜 직접적인(less direct) neural 3D representation을 제안한다. 또한 표면 위치를 결정하기 위해, ray를 따라서 동작하는 RNN으로 구성된 미분 가능한 렌더링 함수도 제안한다.

이러한 기술들이 복잡하고 고해상도인 기하학을 표현할 수 있는 잠재성이 있긴 하지만, 지금까지 낮은 기하학적 복잡도를 가진 단순한 물체에 제한되어 왔고 지나치게 부드러운(oversmoothed) 결과물들을 보여주었다. 우리는 5차원의 radiance field(x, y, z + 2D view-dependent appearance)를 인코딩하는 네트워크를 최적화하는 전략이 더 고해상도의 기하학과 모습을 나타낼 수 있고, 복잡한 장면에서 실사에 가까운 novel view를 렌더링 할 수 있음을 보인다.

View synthesis and image-based rendering (시점 합성과 이미지 기반 렌더링)

특정 시점에서의 dense sampling을 가정하면, 실사에 가까운 새 시점 (photorealistic novel view)은 간단한 light field sample interpolation 기법을 이용해 만들어질 수 있다. Sparser view sampling 을 위해, 컴퓨터 비전 및 그래픽 커뮤니티는 관찰 이미지에서 전통적인 기하학 및 모양 (geometry and appearnce) 표현을 예측함으로써 상당한 발전을 이루었다. 유명한 접근법 중 하나는 diffuse 혹은 view-dependent apperacne를 가지는 mesh-based representation을 사용한다. 미분가능한 래스터라이저와 pathtracer가 경사하강법을 이용하여 mesh representation을 최적화할 수 있다. 그러나 image reprojection 기반의 경사하강법 mesh 최적화는 힘든 경우가 대부분이다. 지역 최소값 문제나 최적화 표면 (loss landscape)의 나쁜 환경 때문이다. 게다가 이러한 전략은 최적화 이전의 초기화에 있어서 고정된 방식(topology)의 template mesh를 요구한다. 그러나 이것은 실제 세계에서는 일반적으로 불가능하다.

3. Neural Radiance Field Scene Representation

우리는 입력이 3D 좌표 $\mathbf{x} = (x,y,z)$와 2D 시점(viewing direction) $(\theta, \phi)$이고, 출력이 RGB 컬러 $\mathbf{c} = (r,g,b)$와 volume density $\sigma$인 5D 벡터 함수로 연속적인 장면 (continuous scene)을 표현한다. 실제로는, 방향(direction)은 3D 카테시안 단위 벡터 $\mathbf{d}$로 표시한다. 우리는 MLP 네트워크 $F_\Theta : (\mathbf{x,d}) \rightarrow (\mathbf{c}, \sigma)$로 이 연속적인 5D 장면 표현 (scene representation)을 추정한다. 그리고 MLP 네트워크의 가중치 $\Theta$를 최적화함으로써 각각의 5D 좌표 입력을 대응하는 volume desnity와 directional emitted color(RGB 컬러 $\mathbf{c} = (r,g,b)$)으로 매핑한다.

핵심적인 공식
$F_\Theta : (\mathbf{x,d}) \rightarrow (\mathbf{c}, \sigma)$

우리는 표현(representation)이 multiview consistent하도록 할 필요가 있다. 따라서 volume density $\sigma$는 좌표 $\mathbf{x}$의 함수로만 정의되고, RGB 컬러 $\mathbf{c}$는 $\mathbf{x}$와 $\mathbf{d}$의 함수로 정의되도록 하였다. 이러한 구조를 달성하기 위해, MLP 네트워크 $F_\Theta$는 먼저 8개의 FC(Fully Connected) 레이어에 3D 좌표 $\mathbf{x}$를 통과시켜서 $\sigma$와 256차원의 feature vector를 얻는다. (이때, 활성화 함수는 ReLU를 사용하고 각 레이어의 출력은 256 차원이다.) 이때 얻은 feature vector를 camrea ray의 viewding direction $\mathbf{d}$와 concat하여 벡터를 얻은후, 다시 하나의 FC 레이어에 넘겨주고, view-dependent한 RGB 컬러 $\mathbf{c}$를 얻는다. (이때 FC 레이어의 활성화 함수는 ReLU, 128차원이다)

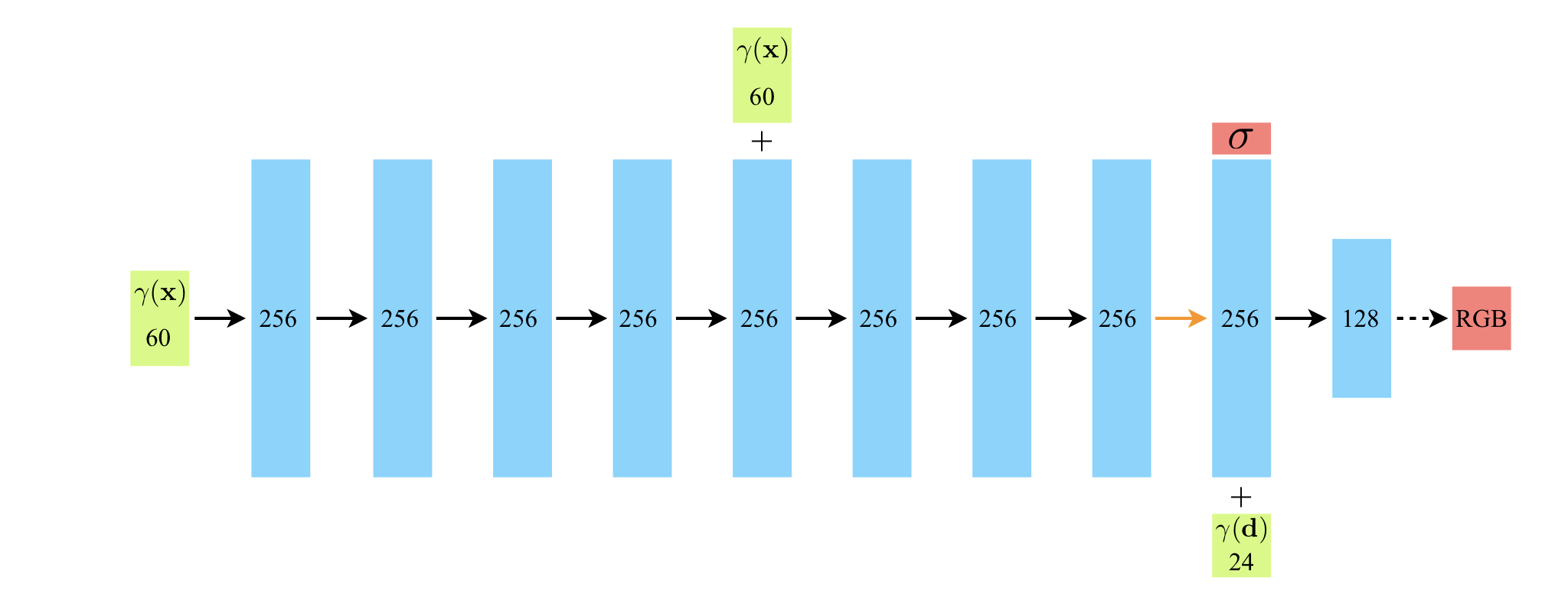
Fig.3는 우리의 방법이 non-Lambertain 효과를 위해서 어떻게 시점(viewing direction)을 활용하는지 보여준다.
Fig.3 : 시점을 고려한 빛(view-dependent emitted radiance)의 시각화. NeRF는 공간적 위치 $\mathbf{x}$와 시점 $\mathbf{d}$를 고려한 5차원 함수를 이용해 RGB 컬러를 얻는다. 이 그림에서, 우리는 배의 두가지 점에서 시점에 따른 색 분포를 비교해보고자 한다. (a)와 (b)는 두 고정된 3D 점에서 카메라 위치에 따른 차이를 보여준다. NeRF는 두 점에서 바뀌는 반사광(specular apperance)을 예측할 수 있으며, (c)는 모든 시점에 걸친 색 분포를 보여준다.

Fig.4는 시점에 대한 고려 없이 ($\mathbf{x}$만을 입력으로 사용함으로써) 훈련된 모델이 반사성(specularities)를 표현하는데 어려움이 있음을 보이고 있다.

Fig.4 : 위 사진은 입력 좌표를 넘겨줄 때 고차원의 positional encoding을 이용하는 우리의 방법이 시점을 고려한 빛을 표현하는데 얼마나 효과적인지를 보여준다. 시점 고려를 제거한 모델은 불도저 타이어 부분의 반사광을 재현하는데 실패하고 있다. Poistional encoding을 제거하는 것은 결과물에서 정교함을 심각하게 저해하여 지나치게 부드러운 모양(oversmoothed appearance)을 생성한다.

4. Radiance Field와 Volume Rendering

5D NeRF는 어떤 장면을 volume desnity와 directional emitted radiance(역주 - 간단하게 말해서 $\mathbf{(\sigma, c)}$)를 가지는 공간상의 점들로 표현한다. NeRF는 전통적인 볼륨 렌더링 (classical volume rendering) 원리를 이용해서 장면을 지나는 빛의 색을 렌더링한다. volume density $\mathbf{\sigma(x)}$는 특정 위치 $\mathbf{x}$의 아주 작은 입자에서 빛이 멈출 차분 확률(differential probability)를 의미한다.(역주 - 간단하게 말하면, 얼마나 빛을 멈추게 할만큼 밀도가 높고 딱딱한가). $t_n$부터 $t_f$까지, 카메라의 빛 $\mathbf{r(t) = o + td}$에 대한 예상 컬러 $\mathbf{C(r)}$은 다음의 수식으로 표현할 수 있다.

$\mathbf{C(r)} = \displaystyle\int_{t_n}^{t_f} T(t) \sigma(\mathbf{r}(t))\mathbf{c(r}(t),\mathbf{d})dt \quad\quad(1)\\ \text{where } T(t) = \text{exp}\left(-\displaystyle\int_{t_n}^{t_f} \sigma(\mathbf{r}(s))ds\right)$

(역주 - 간단하게 $T(t)\sigma\mathbf(r(t))$를 weight로 해석하여 각 컬러에 대한 가중합 정도로 생각할 수 있다.)

$T(t)$는 $t_n$부터 $t$까지 빛을 따라서 누적된 투과도를 의미한다. 즉, $t_n$부터 $t$까지 빛이 진행할 때 어떤 입자에도 부딪히지 않을 확률이다 (역주 - volume density $\sigma$에 반비례 하는 개념). 연속적인 neural radiance field에서 시점을 렌더링 하는 하는 것은 곧 어떤 가상 카메라의 각 픽셀을 통과하는 카메라 빛들에 대한 적분 값 $C\mathbf{(r)}$을 추정하는 작업을 의미한다.

우리는 이 연속적인 적분값을 구적법(quadrature)를 이용하여 수학적으로 근사(estimate)할 것이다. MLP는 위치의 고정된 이산 집합에서만 동작하기 때문에 (be quried at a fixed discrete set of locations), 이산적인 voxel grid의 렌더링에 흔히 사용되는 deterministic quadrature는 해상도에 있어서 제약이 있을 수 밖에 없다. 대신, 우리는 다음과 같은 stratifed sampling 접근법을 사용한다 : [$t_n, t_f$]를 N개의 칸(bin)으로 균등하게 나눈 다음, 각 칸에서 균등 분포를 이용하여 하나의 샘플을 뽑는다.

$t_i \sim \mathcal{U} \left[t_n + \frac{i-1}{N}(t_f - t_n), t_n + \frac{i}{N}(t_f - t_n)\right]\quad\quad(2)$

비록 적분값을 근사하기 위해서 샘플들의 이산 집합을 이용하지만, 최적화 과정에서 MLP가 연속적인 위치에서 평가되는 결과를 가져오기 때문에 (reuslts in the MLP being evaluated at continuous postions over the course of optimization) stratified sampling은 결국 연속적인 장면의 표현을 가능하게 한다. 우리는 이렇게 뽑힌 샘플들을 이용하여 $C\mathbf(r)$을 근사하기 위해 Max의 volume rendering review에서 논의된 quadrature rule을 사용한다.

$\hat {C}(\mathbf{r}) = \displaystyle\sum_{i=1}^{N}T_i\left(1-\text{exp}(-\sigma_i\delta_i)\right)\mathbf{c}_i, \quad\quad (3) \\ \text{where} \quad T_i = \text{exp} \left(-\displaystyle\sum_{j=1}^{i-1}\sigma_j\delta_j\right)$

$\delta_i = t_{i+1} - t_i$는 인접 샘플 간의 거리를 의미한다. $(\mathbf{c}_i, \sigma_i)$ 집합에서 $C(\mathbf{r})$을 계산하는 함수는 미분 가능하고, 알파 값 $\alpha_i = 1 - \text{exp}(-\sigma_i\delta_i)$에 대한 전통적인 알파 합성 문제로 회귀된다.

5. Optimizing a Neural Radiance Field

이전 섹션에서 우리는 neural radiance field를 이용해 장면을 모델링하고, 이를 통해 새로운 시점(novel view)를 렌더링하는데 필요한 중요 요소를 설명했다. 그러나 Section 6.4에서 보인 것처럼, 이러한 요소들만으로는 SOTA를 달성하기 어려웠다. 그래서 우리는 고해상도의 복잡한 장면을 표현하기 위해 두가지 개선점을 제시한다. 첫번째는 입력 좌표에 대한 Positional Encoding이다. 이는 MLP가 고해상도 함수를 더 잘 표현하도록 보조하는 역할을 한다. 두번째는 Hirearchial Sampling이다. 이는 고해상도 표현(high-frequency sampling)을 더 효과적으로 샘플링하도록 도와주는 과정이다.

5.1 Positional Encoding

비록 neural network이 함수 근사에 일반적으로 잘 사용되지만, 우리는 네트워크 $F_\Theta$를 바로 입력좌표 $xyz\theta\phi$로만 운영하는 것은 잘 작동하지 않는 다는 것을 확인할 수 있었다. 이는 Rahaman의 최근 연구에서도 동일하게 나타나는데, 깊은 네트워크가 lower-frequency function을 학습하는 것에만 편항되어 있다는 것을 보여주었다. (역주 - 전반적으로 네트워크의 표현력이 낮다는 이야기) 그들은 또한 high frequency function을 이용하여 입력을 고차원으로 변환하면, 네트워크가 데이터를 더 잘 학습하고 표현력도 좋아진다는 것을 보였다.

우리는 이러한 발견을 neural scene representation 측면에서 레버리지(leverage)하여, $F_\Theta$를 다음과 같이 두 함수의 합성으로 변형한다. $F_\Theta = F_\Theta' \circ \gamma$. (전자는 학습되지만 후자는 학습되지 않는 함수이다.) 그리고 이 방법이 성능을 상당히 개선함을 보인다. $\gamma$는 $\mathbb{R}$에서 $\mathbb{R}^2$으로의 매핑 함수이고, $F_\Theta'$는 일반적인 MLP이다. 우리가 사용하는 인코딩 형식은 수식적으로 다음과 같다 :

$\displaystyle\gamma(p) = \left(\sin(2^0\pi p), \; \cos(2^0 \pi p), \; \cdots \; \sin(2^{L-1} \pi p), \; \cos(2^{L-1}\pi p)\right) \quad\quad (4)$

함수 $\gamma(\cdot)$은 ([-1,1]로 정규화된) 세개의 좌표 값 $\mathbf{x}$와 ([-1,1]의 값을 가지는) Cartesian 시점 방향 단위 벡터 $\mathbf{d}$에 적용된다. 우리는 실험에서 $\gamma(\mathbf{x})$에 대해서 $L = 10$, $\gamma(\mathbf{d})$에 대해서 $L = 4$를 적용했다.

비슷한 maaping이 유명한 Transformer 아키텍처에도 적용되는데, 그쪽에서도 역시 Positional encoding이라고 부른다. 하지만 Transformer에서는 목적이 조금 다른데, 순서를 포함하지 않고 있는 구조의 입력으로 사용하여 시퀀스의 토큰마다 이산적인 위치를 부여하도록 사용된다. 이와 대조적으로, 우리는 연속적인 입력 좌표를 좀 더 고차원으로 매핑하여 MLP가 higher frequency function을 더 잘 근사하도록 하기 위해 사용한다. 사영(projection)에서 3D 단백질 구조를 모델링 하는 문제의 과제에서도 비슷한 입력 좌표 매핑을 이용한다.

5.2 Hirearchial volume sampling

카메라 빛을 따라 N개의 지점에서 neural radiance field network의 값을 구해 렌더링 하는 전략은 사실 비효율적이다. 렌더링 이미지에 별 기여를 하지 않는 빈 공간과 차광된 공간이 여전이 반복해서 샘플링되기 때문이다. 우리는 volume rendering에 대한 이전의 연구에서 영감을 받아, 최종 렌더링에 대한 예상 기여도에 비례하여 샘플들을 할당하는 방법을 통해 렌더링 효율을 증가시키는 hirearchial representation을 제안한다.

장면을 표현하기 위해 단순히 하나의 네트워크만을 사용하는 대신, 우리는 두가지 네트워크를 동시에 최적화한다. 하나는 coarse 네트워크, 다른 하나는 fine 네트워크이다.

우리는 먼저 stratified sampling을 통해 $N_c$개의 지점에서 샘플링을 하여 첫번째 위치 집합을 얻고, 이 지점에서 방정식(2)와 (3)대로 coarse network의 값을 구한다. Coarse network의 출력값이 주어졌을 때, 우리는 각 volume에 상관 있는 방향으로 샘플이 편향되도록 샘플링을 진행한다. 이렇게 하기 위해, 우리는 coarse 네트워크의 알파 합성된 컬러 $\hat{C}_c(\gamma)$를 모든 샘플된 컬러 $c_i$에 대한 가중합으로 재작성한다:

$\hat{C}_c(\gamma) = \displaystyle\sum_{i=1}^{N_c}w_ic_i, \quad\quad\quad\quad (5) \\ w_i = T_i(1-\text{exp}(-\sigma_i\delta_i))$

가중치들을 $\hat{w}_i = w_i / \sum_{j=1}^{N_c}w_j$로 정규화하면, 빛을 따라 piecewise-constant PDF(조각마다 상수 확률밀도함수)를 얻을 수 있다. Inverse transform sampling을 이용해 이 분포로부터 다시 두번째 위치 집합 $N_f$개의 위치를 샘플링한다. 그리고 첫번째 집합과 두번째 집합의 합집합으로 fine 네트워크의 값을 얻는다. 그리고 방정식 (3)과 $N_c + N_f$개의 샘플들을 이용하여 최종적으로 렌더링된 빛의 색 $\hat{C}_f(\mathbf{r})$를 얻는다. 이 과정은 색이 뚜렷할 것으로 예상되는 지점에서 더 많은 샘플링을 하도록 한다. 이는 importance sampling과 목표가 비슷하다. 하지만 우리는 각 샘플을 전체 적분에 대한 독립적인 확률 추정치로 생각하는 대신, 샘플된 값을 모든 정의역에 대한 비균등 이산화로 사용한다. (We use the sampled values as a nonuniform discretization of the whole integration domain rather than treating each sample as an independent probabilistic estimate of the entire integral)(역주 - 뭔소린지 모르겠다...)

5.3 구현 과정의 세부사항

우리는 장면마다 서로 다른 네트워크를 최적화한다. 이 작업은 장면을 촬영한 RGB 이미지들의 데이터셋, 대응하는 카메라 위치, 고유한 파라미터, 장면 경계(scene bounds)를 필요로 한다.
각각의 최적화 iteration에서, 우리는 데이터셋의 모든 픽셀의 집합으로부터 카메라 빛을 배치 단위로 샘플링 한다. 그 후 5.2절에 묘사된대로 hirearchial sampling을 진행하여 coarse 네트워크에서 $N_c$개의 샘플을 뽑고, fine 네트워크에서 $N_c + N_f$개의 샘플을 뽑는다. 그 후에는 두 샘플 집합으로부터 빛의 색을 렌더링 하기 위해 4절의 volume rendering을 진행한다. 손실 함수는 단순히 coarse와 fine 네트워크가 렌더링한 색과 true 픽셀 색간의 전체 squared error이다.

$\displaystyle\mathcal{L} = \sum_{r \in \mathcal{R}} \left[\left|\left| \hat{C}_c(\mathbf{(r)} - C(\mathbf{r})\right|\right|_2^2 + \left|\left| \hat{C}_f(\mathbf{(r)} - C(\mathbf{r})\right|\right|_2^2\right]\quad\quad$ (6)

$\mathcal{R}$은 은 각 배치에서 ray 집합을 의미한다. 그리고 $C(\mathbf{r}), \hat{C}_c(\mathbf{r}), \hat{C}_f(\mathbf{r})$은 각각 ray $\mathbf{r}$에 대한 정답, coarse 네트워크의 예측값, fine 네트워크의 예측값(RGB 컬러)이다. 물론 최종 렌더링은 $\hat{C}_f(\mathbf{r})$를 이용해 진행하지만, coarse 네트워크가 fine 네트워크에 샘플 할당에 이용되기 때문에 $\hat{C}_c(\mathbf{r})$의 값 또한 minimize한다.

우리의 실험에서, 4096 ray 배치, $N_c=64$, $N_f=128$의 값을 사용했다. Adam optimizer를 사용하였으며, $5 \times 10^{-4}$의 초기 learning rate 값을 사용하고, 학습 과정에서 $5 \times 10^{-5}$로 exponentially decay 하도록 설정했다. (다른 Adam optimizer의 값들은 기본값으로 놔두었다 : $\beta_1 = 0.9$, $\beta_2 = 0.999$, $\epsilon = 10^{-7}$). NVIDIA V100 GPU에서 한 장면을 학습 및 수렴하는 데에는 100k-300k iteration (약 하루~이틀)이 요구되었다.