[알고리즘] 다이나믹 프로그래밍(Dynamic Programming, DP)

Dynamic Programming 기본

• 입력 크기가 작은 부분 문제들을 모두 해결한 후 그 해들을 이용하여 보다 큰 크기의 부분 문제들을 해결하여 최종적으로 원래 주어진 입력의 문제를 해결하는 알고리즘
• 부분문제들 사이에 의존적 관계가 존재함(부분문제들이 서로 영향을 미침)
• 한 가지 문제에 대해서 단 한 번만 풀도록 만들어주는 알고리즘

---

Dynamic Programming 조건

중복 부분문제 구조 (Overlapping Subproblems)

1. 큰 문제를 작은 문제로 나눌 수 있음
2. 작은 문제에서 구한 답은 그것을 포함하는 큰 문제에서도 동일함

같은 문제가 항상 정답이 같고, 반복적으로 일어난다는 점을 활용해 메모이제이션으로 큰 문제를 해결해 나가는 것 -> 테이블 참조를 통해 중복적인 계산을 줄임
반복적인 관계를 명시적으로 표현하기 위해 일반적으로 수학적 도구인 점화식을 사용

최적 부분문제 구조 (Optimal Substructure)

주어진 문제가 최적화의 원칙을 만족해야만 효율적인 적용이 가능함
DP 방법 자체가 큰 문제의 최적해를 작은 문제의 최적해들을 이용하여 구하는 방법이므로, 큰 문제의 최적해가 작은 문제들의 최적해들로 구성되지 않는다면 적용할 수 없음

최적화의 원칙(Principle of Optimality)
어떤 문제에 대한 해가 최적일 때, 그 해를 구성하는 작은 문제들의 해 역시 최적이어야함

메모이제이션(Memoization)

• 한 번 구한 결과를 메모리 공간에 메모해두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법. 캐싱(Caching) 이라고도 함

---

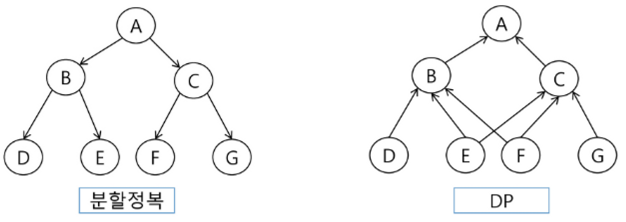
분할 정복과 비교

분할 정복

부분문제들 간에 관계가 없음
부분 문제를 재귀적으로 해결
부분 문제의 해를 결합
하향식(Top-Down) 방식으로 접근

다이나믹 프로그래밍

부분문제들 간에 관계가 존재하지 않으면 적용할 수 없음 => 부분 문제들은 더 작은 부분문제들을 공유함
모든 부분 문제를 한번만 계산하여 결과를 저장하고 이를 재사용함
부분문제들 사이에 의존적 관계가 존재하고, 이러한 관계는 문제에 따라 다르며, 대부분의 경우 뚜렷하게 보이지 않아 함축적인 순서라고함
상향식(Bottom-Up) 방식으로 접근

---

구현 방식

탑다운, 하향식(Top-Down)

• 큰 문제를 해결하기 위해 작은 문제를 호출하는 방식

바텀업, 상향식(Bottom-Up)

• 작은 문제부터 차근차근 답을 도출해가는 방식

Bottom-Up 은 해결이 용이하지만, 가독성이 떨어짐
Top-Down 은 가독성이 좋지만, 코드 작성이 힘듦

• 다이나믹 프로그래밍으로 해결할 때는 작은 문제부터 해결하는 것이 좋음

접근 방식

1. 최적해 구조의 특성을 파악
   • 문제를 부분문제로 나누기
2. 최적해의 값을 재귀적으로 정의
   • 부분문제의 최적해 값에 기반하여 문제의 최적해 값을 정의
3. 상향식 방법으로 최적해의 값을 계산
   • 가장 작은 부분문제부터 해를 구한 뒤 테이블에 저장
   • 테이블에 저장되어있는 부분문제의 해를 이용하여 점차적으로 상위 부분문제의 최적해를 구함

---