
Bias는 모델에서 예측한 값과 데이터의 실제 값 사이의 차이를 나타낸다.
Variance는 예측 값이 서로 얼마나 분산되어 있는지 설명한다.
다양하게 값이 나오면 variance가 크다.
Underfit : error 많이 생김. Linear regression. 트랜드 분석.
Overfit : error 별로 없음.
위의 두개를 방지하기 위해 bias와 variance를 고려.
C와 감마
Cross validation
ex.100개의 data를 5등분으로 k fold(100/k개씩 쪼개서 총 k번 반복. K=5면 k=1일때 1~20개, k=2면 21~40까지 해서 test와 train이 5번 섞일 수 있도록 하는 것이 k fold.
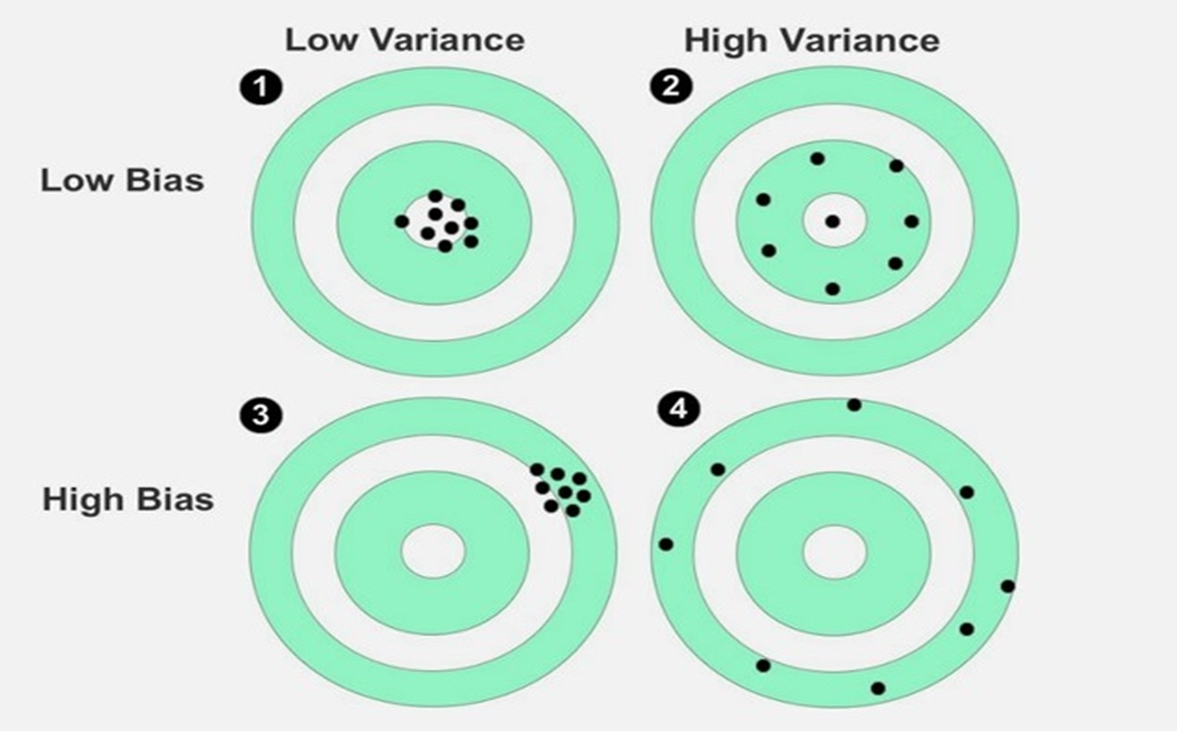
표시된 점은 제공된 train 또는 test 데이터를 기반으로 모델의 개별 예측을 나타낸다.
1번의 경우 예측값과 실제값이 비슷한 가장 ideal한 형태이다.
2번의 경우 disperse 된 것이다.
3번의 경우 center of target에서 멀리 떨어져있어서 실제값과 예측값의 gap이 크다.
1. Low Bias, Low Variance 가장 이상적
2. Low Bias, High Variance
3. High Bias, Low Variance
4. High Bias, High Variance
그러나 실제로는 최적 bias와 최적 variance 사이에 트레이드 오프가 있습니다.
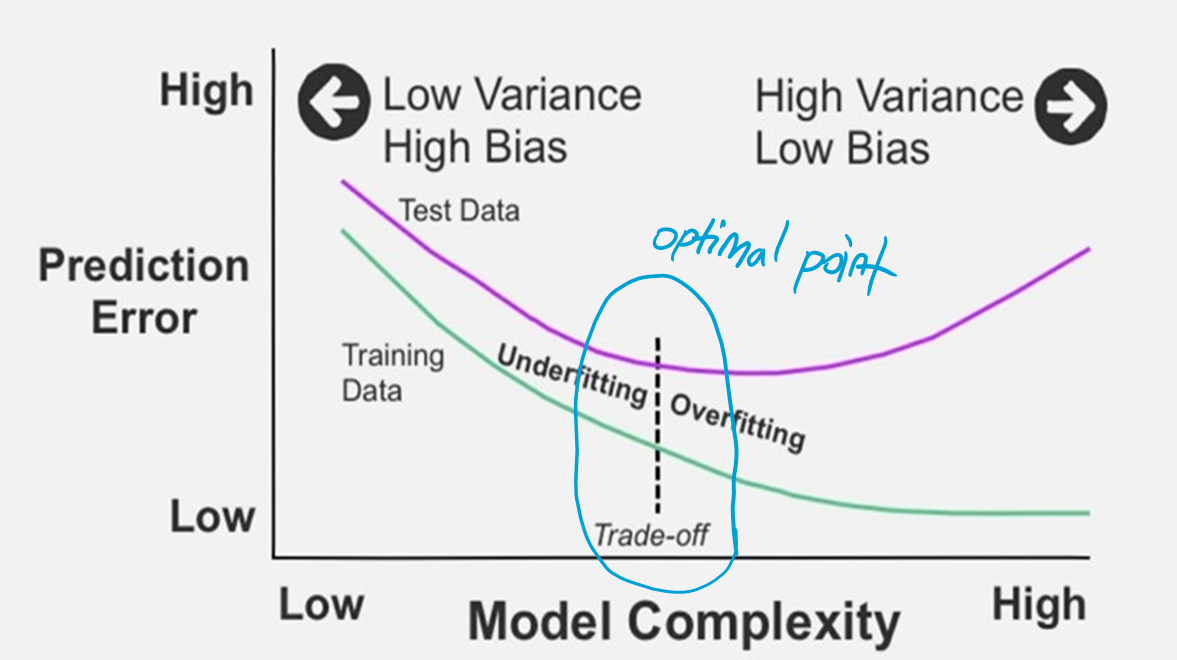
두 개의 곡선 중 위쪽 곡선은 테스트 데이터를 나타내고 아래쪽 곡선은 train 데이터를 나타낸다.
Plot의 중간에는 train 데이터와 테스트 데이터 사이의 예측 오류의 최적의 균형이 있다.
이 중간 지점은 bias-variance 절충의 전형적인 예이다.
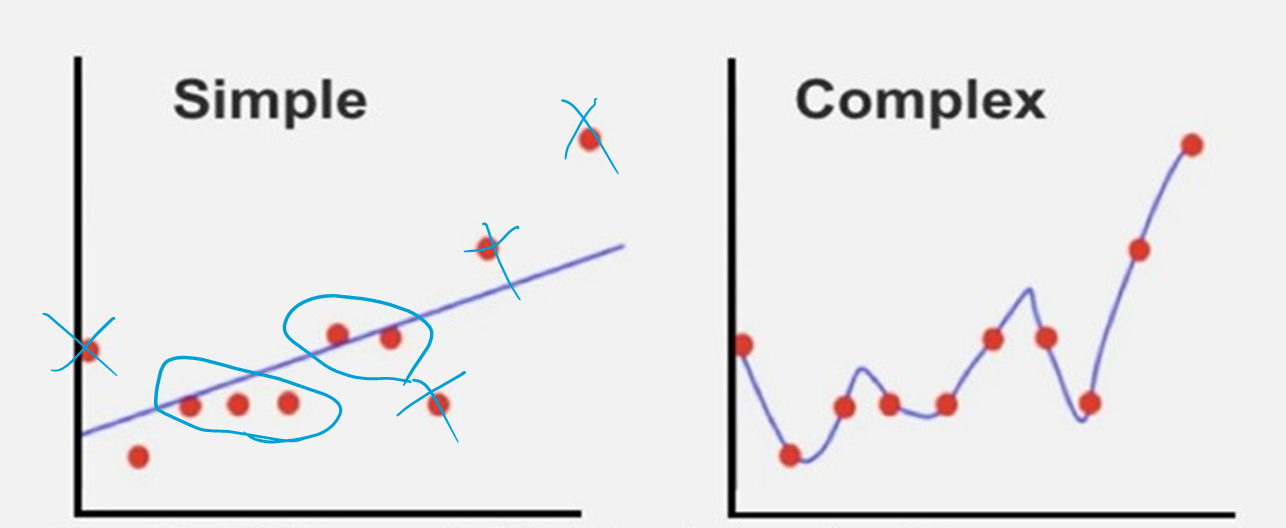
왼쪽 : Underfitting(Low variance, High bias)
오른쪽 : Overfitting(High variance, Low bias)
Overfitted 모델은 train 데이터를 사용하여 정확한 예측을 생성하지만 테스트 데이터를 사용하여 예측을 하는 데 덜 정확하다. 테스트 데이터나 새 데이터로 테스트하면 정확도가 떨어진다.
underfit은 train 데이터와 테스트 데이터 모두에 대해 부정확한 예측으로 이어질 수 있다. underfitting의 일반적인 원인에는 가능한 모든 조합을 적절하게 처리하기에 충분하지 않은 train 데이터와 train 및 테스트 데이터가 적절하게 무작위화되지 않은 상황이 포함된다.
선형 회귀에서 비선형 회귀로 전환하면 분산을 증가시켜 bias를 줄일 수도 있다. 또는 k-NN에서 "k"를 늘리면 분산이 최소화된다(더 많은 이웃을 평균화하여). 세 번째 예는 단일 결정 트리(overfit되기 쉬운)에서 많은 결정 트리가 있는 임의 forest로 전환하여 분산을 줄이는 것이다.
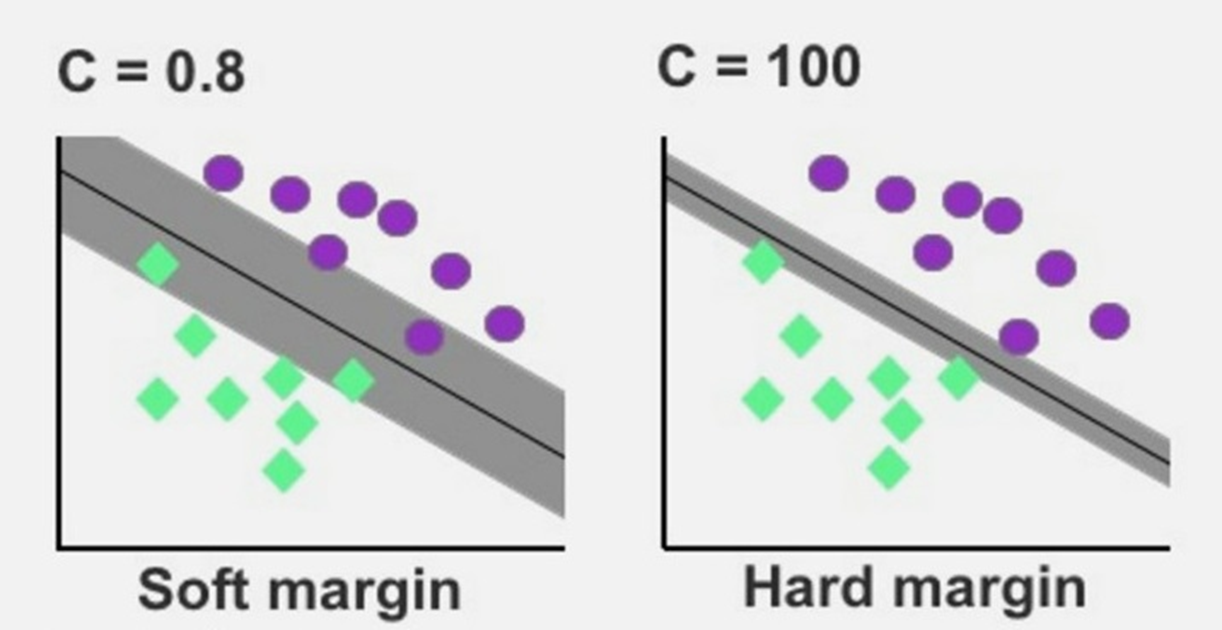
C가 0에 가까울수록 soft margin. C를 optimize하는 것이 중요.