백트래킹

• 모든 경우의 수를 탐색하는 알고리즘
• DFS나 BFS를 이용할 수 있다.
• 효율을 위해 탐색하지 않아도 되는 곳을 미리 막는 것을 가지치기라고 한다.
• 자바스크립트는 재귀 효율이 나쁘기 때문에 DFS를 구현할 경우 스택을 이용하는 것이 좋다.
  • 코테에선 이를 고려하여 재귀로 작성해도 풀 수 있도록 문제를 제출하는 경우도 있다.
• 탐색에서 순환이 발생할 수 있다면 BFS를 이용하는 것이 편하다.

💡 백트래킹의 핵심은 가지치기!
가지치기를 얼마나 잘하느냐에따라 효율성을 결정한다

어떻게 작성할 것인가?

• 우선 모든 경우의 수를 찾을 수 있도록 코딩
• 이후 문제에서 특정한 조건을 만족하는 것만 탐색하고 나머지는 탐색하지 않도록 조건문을 작성한다.
• 즉, 절대로 답이 될 수 없는 것은 탐색을 종료한다.

N-Queen 문제

https://school.programmers.co.kr/learn/courses/30/lessons/12952

DP 동적계획법

• 해결한 작은 문제로 큰 문제를 해결하는 문제 풀이 방식
• 그리디나 백트래킹처럼 틀정 알고리즘이 아닌 문제 해결 방식을 의미한다.
• Dynamic Programming라고 부른다.
• 메모리를 많이 사용하는 대신 빠른 성능을 자랑한다.
• 두가지 방법론이 있다.
  • 메모이제이션 Memoization
  • 타뷸레이션 Tabulation

메모이제이션 Memoization

• 하향식 접근법
• 동적 계획법에서 작은 문제들의 결과는 항상 같다.
• 따라서 이 결과들을 메모리에 저장해 필요할 때 꺼내 쓰는 것이 메모이제이션이다.
• 예시) 피보나치 수열

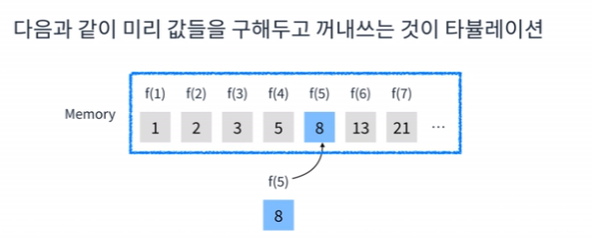
타뷸레이션

• 상향식 접근법
• 필요한 값들을 미리 계산해두는 것
• 메모이제이션은 필요할때 계산한다면(Lazy evaluation)
  타뷸레이션은 미리 계산해둔다(Eager evaluation)
• 보통 코테에선 메모이제이션을 쓰는 경우가 대부분이다.
  

동적 계획법 문제 어떻게 접근할까?

• DP 유형은 키워드만으로 DP 문제임을 알기 어렵다.
• 그렇기 때문에 문제 유형을 알 수 없다면 다음을 확인해보자.
  • 가장 작은 문제를 정의할 수 있는지?
  • 작은 문제를 통해 큰 문제를 해결할 수 있는 규칙이 있는지?
• 위 두 가지가 가능하다면 DP문제다.
• 간혹 메모리를 너무 사용하여 통과 못하는 경우도 있다.
  • 이런 경우엔 DP를 이용할 수 있지만 보통 코테에서 자주 나오지 않는다.