회고
오늘은 코테 문제들을 푸는 수업이 많았다. 프로그래머스 Lv.1~Lv.2를 간신히 푸는 나에게 Lv.3의 문제들 정말 너무 어려웠다...😮 이해하는데 기본 30분이상 걸리는 것 같다. 그래도 문제에 대한 접근법들을 여러가지 생각해가면서 실패도 많이 해보고 성공도 해보는 경험이 즐거웠다. 좀 더 시간투자를 해서 문제해결능력을 기르자. 오늘의 회고 TIL 끝!😊
이진탐색
선형 탐색
- 순서대로 하나씩 찾는 탐색 알고리즘 . O(n)
- 예시) 정리안된 책장에서 원하는 책을 찾는 방법
이진 탐색
- 정렬 되어있는 요소들을 반씩 제외하며 찾는 알고리즘. O(log n)
- 요소들이 이미 정렬되어 있어야 사용 가능한 알고리즘
예시) Up/Down 게임
이진 탐색의 특징
반드시 정렬이 되어있어야 사용할 수 있다.
배열 혹은 이진 트리를 이요하여 구현할 수 있다.
O(logn)인 만큼 속도가 굉장히 빠르다
배열을 이용한 구현방법
const array = [1, 1, 5, 124, 400, 599, 1004, 2876, 8712];
function binarySearch(array, findValue) {
let left = 0;
let right = array.length - 1;
let mid = Math.floor((left + right) / 2);
while (left < right) {
if (array[mid] === findValue) {
return mid;
}
if (array[mid] < findValue) {
left = mid + 1;
} else {
right = mid - 1;
}
mid = Math.floor((left + right) / 2);
}
return -1;
}
console.log(binarySearch(array, 2876));
console.log(binarySearch(array, 1));
console.log(binarySearch(array, 500));이진탐색 트리를 이용한 구현방법
이진 탐색을 위한 이진 트리로 왼족 서브 트리는 루트보다 작은 값이 모여있고 오른쪽 서브 트리는 루트보다 큰 값이 모여있다. 이 규칙을 지키면서 요소를 추가해주면 된다.
이진탐색 트리 요소 삭제
- 단말 정점(leaf node)를 삭제하는 경우 ⇒ 별다른 처리 없이 부모 정점과의 연결을 끊으면 된다.
- 제거할 정점이 하나의 서브 트리를 가지는 경우 ⇒ 제거되는 정점의 부모 간선을 자식 정점을 가르키게 바꾸면 된다.
- 두 개의 서브 트리를 가지는 경우 ⇒ 왼쪽 서브 트리의 가장 큰 값 혹은 오른쪽 서브 트리의 가장 작은 값과 교체하면 된다. 이 경우 교체된 정점의 좌우 자식이 없다면 제거되는 정점의 링크로 대체된다.
이진 탐색 트리의 문제점
- 최악의 경우 한쪽으로 편향된 트리가 될 수 있다.
- 그런 경우 순차 탐색과 동일한 시간복잡도를 가진다.
- 이를 해결하기 위해 다음과 같은 자료구조를 이용 할 수 있다.
- AVL 트리
- 레드-블랙 트리
BFS/DFS
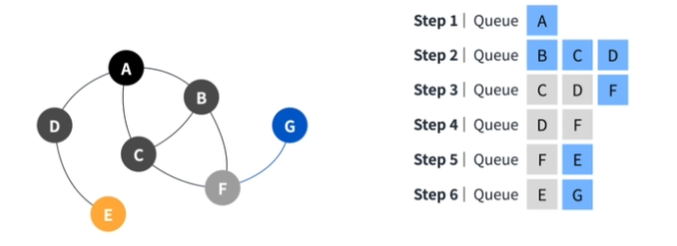
BFS 너비 우선 탐색
그래프 탐색 알고리즘으로 같은 깊이에 해당하는 정점부터 탐색하는 알고리즘
- Queue를 이용하여 구현한다.
- 시작 지점에서 가까운 정점부터 탐색한다.
- V가 정점의 수, E가 간선의 수일 때 BFS의 시간 복잡도는 O(V+E)이다.
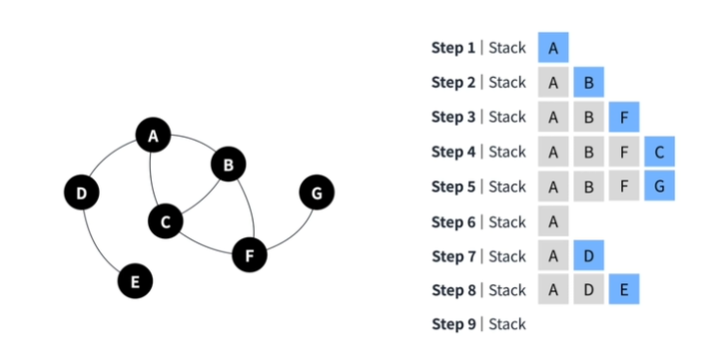
깊이 우선 탐색
그래프 탐색 알고리즘으로 최대한 깊은 정점부터 탐색하는 알골리즘
- stack을 이용하여 구현한다
- 시작 정점에서 깊은 것 부터 찾는다
- V가 정점의 수,E가 간선의 수일때 시간복잡도 O(V+E)
그리디
- 매 선택에서 지금 이 순간 가장 최적인 답을 선택하는 알고리즘이다. 최적해를 보장해주지 않는다.
- 보통 최적해를 구하는 알고리즘보다 빠른 경우가 많다.
- 크루스칼, 다익스트라 알고리즘 등에 사용된다.
- 코테에서 직관적인 문제 풀이에 적합하다.
프로그래머스 Lv.2 큰 수 만들기 문제
https://school.programmers.co.kr/learn/courses/30/lessons/42883
function solution(number, k) {
let cnt = 0;
const result = [];
for(let i = 0; i <number.length; i++){
//stack의 top과 number[i]를 비교해서 top이 작으면 stack에서 pop해준다.
while(number[i]> result[result.length-1] && cnt < k){
result.pop();
cnt++
}
//처음부터 넣어주면 다른 결과값이 나온다.특히 테스트 Case1같은 경우 top이 9가 되서 틀린 답이 나옴
//갯수를 채워주도록 뒤에 위치시켜야한다.
if(result.length < number.length -k){
result.push(number[i]);
}
}
return result.join('');
}