
4.1 선형 회귀
데이터들 중 가장 적절한 선을 찾는 것
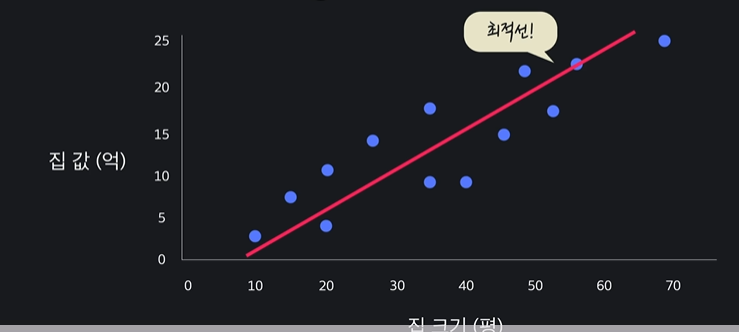
가장 잘맞는 선 = 최적선
단순하면서도 유용하고 다른 알고리즘의 기반이 된다 !
4.2 선형 회귀 용어
선형회귀는 머신러닝의 지도학습, 비지도학습, 강화학습 중에 지도학습에 속한다 !
그리고 지도학습은 분류와 회귀로 나뉘는데 선형회귀는 회귀에 속한당
- 목표 변수 : 맞추려고 하는 값 (target variable / output variable)
- 입력 변수 : 맞추는데 사용하는 값 (input variable / feature)
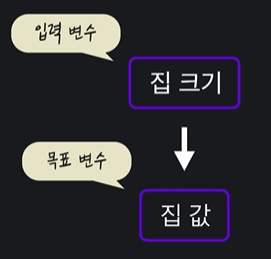
데이터 표현법

4.3 가설 함수
선형회귀의 목표 = 최적선을 찾는 것 !
최적선을 찾기 위해 여러 가상의 함수를 사용하는데 이 함수를 가설함수``(hypothesis function)라고 한다
우리가 찾으려는 선은 일직선이기 때문에 이는 일차함수가 되고 y = ax +b에서 a와 b를 찾으려는 것이다 !
가설함수에선 y = ax +b 이렇게 쓰지 않고
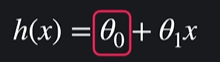
이런 형식으로 쓴다 -> 선형회귀의 임무 : 가장 적절한 세타들의 값을 찾는 것
4.4 평균 제곱 오차 (MSE)
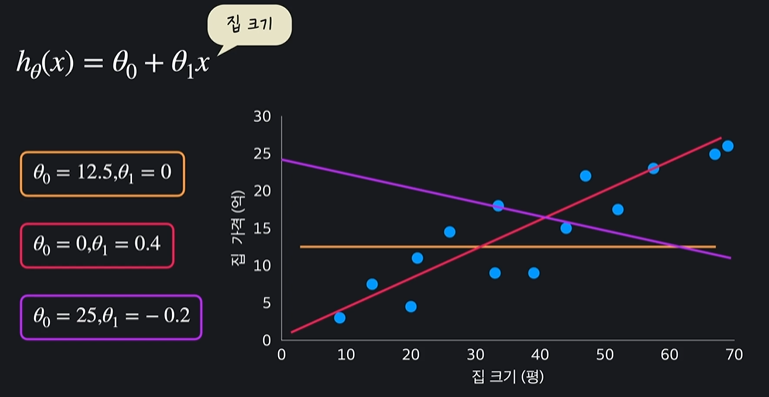
가설함수 평가법
- 평균 제곱 오차 (Mean Square Error) : 데이터들과 가설함수가 평균적으로 얼마만큼 떨어져있는지 알아보는 법
= (오차값들의 제곱)/데이터의 개수
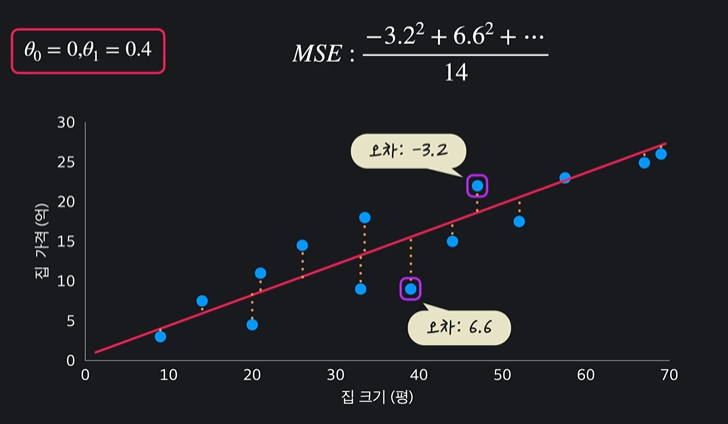
평균 제곱 오차가 크면 안좋은 가설함수이다
근데 왜 오차의 제곱을 더할까? -> 오차가 양수, 음수로 나오기 때문 ! & 더 큰 오차를 부각시키기 위해서
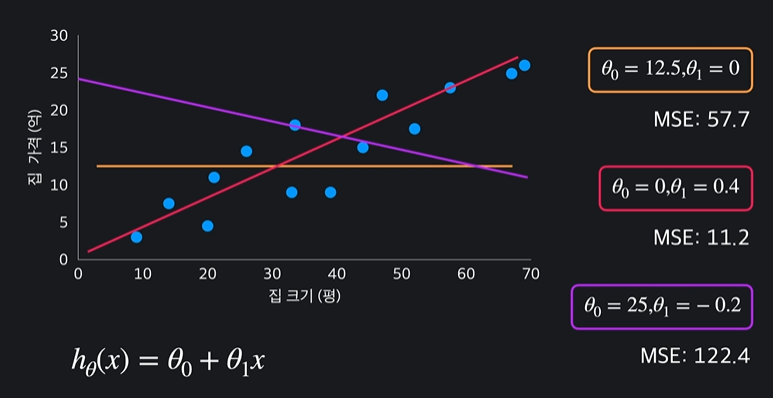
두번째 가설함수의 평균 제곱오차 값이 가장 작기 때문에 가장 적절한 함수이다
4.5 평균 제곱 오차 일반화
평균제곱오차를 표현하는 수학식
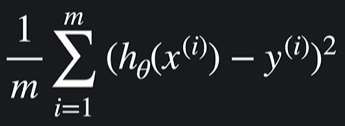
h는 가설함수 x는 인풋, y는 아웃풋 / i는 몇번째를 나타내서 i번째 인풋, i번째 아웃풋을 나타냄
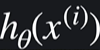
이거는 i번쨰 데이터 예측값이고
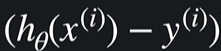
이거는 i번째 데이터 예측 오차이다

그리고 이를 제곱시킨 것

i=1부터 i=m까지 하나씩 대입하고 결과를 다 더한다는 뜻
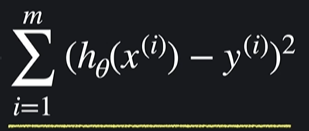
모든 데이터 제곱의 합
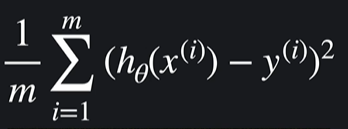
마지막에는 1/m (m= 데이터의 개수)으로 나눠서 평균을 내준다
4.6 손실 함수
: 가설 함수의 성능을 평가하는 함수
손실함수가 작으면 가설함수가 데이터에 잘맞는 것이고 손실함수가 크면 가설함수가 데이터에 잘 맞지 않는다는 것이다.
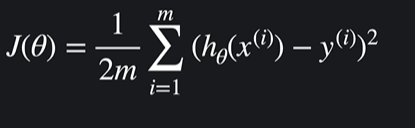
-
특정 가설함수의 평균 제곱오차가 크면 손실함수의 아웃풋이 크다는 것 -> 손실이 크기 때문에 가설함수가 안좋은 것이다
-
특정 가설함수의 평균 제곱오차가 작으면 손실함수의 아웃풋이 작다는 것 -> 손실이 작기 때문에 가설함수가 좋은 것이다
손실함수 J의 인풋은 세타이고 가설함수에서 우리가 바꾸는 값들은 x가 아니라 세타이기 때문에 손실함수의 아웃풋은 세타의 설정값에 달려있다
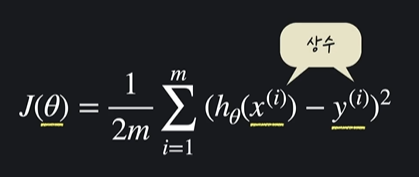
손실함수에선 x와 y가 상수라고 볼 수 있다
4.7 경사 하강법 개념
: 손실 함수의 아웃풋을 최소화하는 방법 중 하나
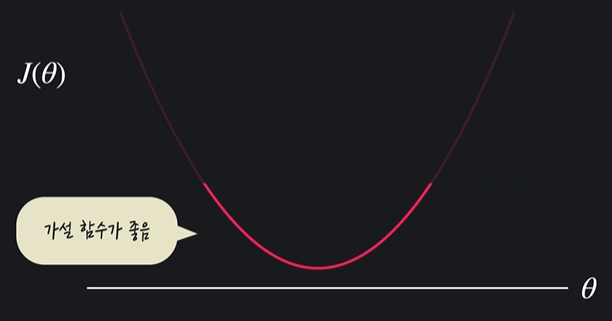
최소화 하려면 극소점을 찾고자 할 것이다 !
-> 기울기에 비례하는 만큼 세타를 움직임 -> 점점 개선이 됨 (= 극소점과 가까워짐) -> 극소점을 찾게 된다
4.8 경사 하강법 테크닉
극소점을 찾기 위해선 계속 내려가야함 !
이 때 우리는 손실함수의 기울기를 활용해야한다

ㄴ 세타들을 새롭게 업데이트 했다고 볼 수 있음
주의! 세타0을 엄데이트 하고 나서 세타 1을 업데이트 하려고 하면 세타 1의 인풋에 업데이트된 세타0이 들어갈 수 있는데 이 땐 원래 세타0을 넣어야한다
4.9 선형 회귀 구현하기 쉽게 표현하기
가설함수
원래 가설함수 hθ(x) = θ0 + θ1x의 x는 입력 변수를 나타내는데 이를 벡터라고 생각할 수도 있다
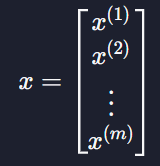
이 데이터들을 원래 가설함수에 대입하면
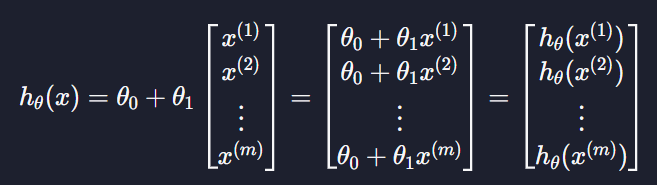
이렇게 되고 그러면 계산하고 싶은 모든 입력 변수에 대한 예측 값을 한 번에 계산할 수 있다
예측 오차
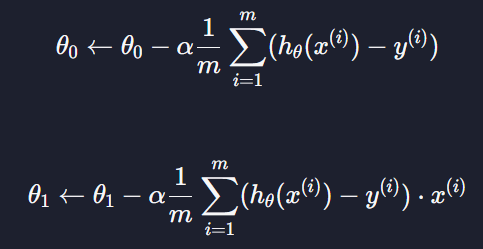
경사 하강법 공식에서
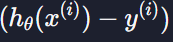
이 부분을 벡터로 생각하면
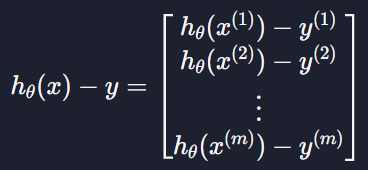
이렇게 만들 수 있다 = 모든 데이터들의 예측 값과 실제 목표 변수 값의 차이를 한 번에 표시할 수 있는 것
이 계산한 값을 우리는 error라고 부르겠음
경사 하강법
벡터 error를 사용해서 표현해보자
식에서
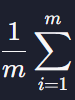
는 모든 데이터의 평균을 구하라는 식이다
벡터 error의 모든 원소의 평균을
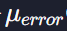
라고 표현할 수 있는데 그렇게 되면 세타들을 업데이트 하는 공식을

이렇게 나타낼 수 있다
θ1은

이 부분을 계산해줘야되기 때문에 조금 더 복잡한데 이는
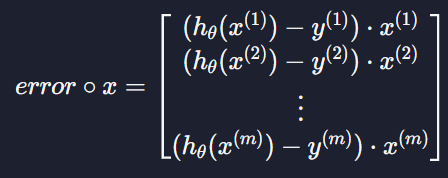
이렇게 표현할 수 있다
그럼 θ1을 표현하는 식이 나온다
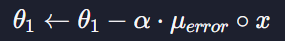
4.10 (실습) 선형 회귀 가설 함수 구현하기
이번 과제에서는 가설 함수를 사용해서 주어진 데이터를 예측하는 코드를 구현해 보겠습니다. prediction이라는 함수로 구현할 건데요. 이 함수에 대해서 설명드릴게요.
prediction 함수
prediction 함수는 주어진 가설 함수로 얻은 결과를 리턴하는 함수입니다. 파라미터로는 θ0를 나타내는 숫자형 변수 theta_0, θ1를 나타내는 숫자형 변수 theta_1, 그리고 모든 입력 변수 벡터 x들을 나타내는 numpy 배열 x를 받죠.
prediction 함수는 x의 각 요소의 예측값에 대한 numpy 배열을 리턴합니다.
numpy 배열과 연산들을 이용해서 prediction 함수를 작성해보세요.
numpy 배열과 숫자형 덧셈
numpy 배열과 일반 숫자형을 더하면 numpy 배열의 모든 요소에 해당 숫자형이 더해집니다. 이걸 사용해서 과제를 풀어보세요!
np_array = np.array([1, 2, 3, 4, 5])
5 + np_array # [6, 7, 8, 9, 10]code
import numpy as np
def prediction(theta_0, theta_1, x):
h = theta_0 + theta_1 * x
return h
# 테스트 코드
# 입력 변수(집 크기) 초기화 (모든 집 평수 데이터를 1/10 크기로 줄임)
house_size = np.array([0.9, 1.4, 2, 2.1, 2.6, 3.3, 3.35, 3.9, 4.4, 4.7, 5.2, 5.75, 6.7, 6.9])
theta_0 = -3
theta_1 = 2
prediction(theta_0, theta_1, house_size)
4.11 (실습) 선형 회귀 예측 오차 구현하기
prediction_difference함수
prediction_difference함수는 선형 회귀 구현하기 쉽게 표현하기 레슨에서 본 error 처럼 모든 데이터의 예측 값과 실제 목표 변수의 차이를 리턴합니다.
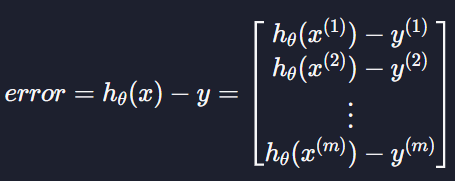
파라미터로는 θ0 를 나타내는 theta_0, θ1 를 나타내는 theta_1, 입력 변수 벡터를 나타내는 x, 그리고 목표 변수 벡터를 나타내는 y를 갖습니다.
theta_0, theta_1, 그리고 x를 이용해서 모든 예측값들을 벡터를 계산하고(저번 과제에서 작성했던 prediction 함수를 사용하세요!), y와의 차이를 벡터로 리턴합니다.
code
import numpy as np
def prediction(theta_0, theta_1, x):
return theta_0 + theta_1 * x
def prediction_difference(theta_0, theta_1, x, y):
"""모든 예측 값들과 목표 변수들의 오차를 벡터로 리턴해주는 함수"""
return prediction(theta_0, theta_1, x) - y
# 입력 변수(집 크기) 초기화 (모든 집 평수 데이터를 1/10 크기로 줄임)
house_size = np.array([0.9, 1.4, 2, 2.1, 2.6, 3.3, 3.35, 3.9, 4.4, 4.7, 5.2, 5.75, 6.7, 6.9])
# 목표 변수(집 가격) 초기화 (모든 집 값 데이터를 1/10 크기로 줄임)
house_price = np.array([0.3, 0.75, 0.45, 1.1, 1.45, 0.9, 1.8, 0.9, 1.5, 2.2, 1.75, 2.3, 2.49, 2.6])
theta_0 = -3
theta_1 = 2
prediction_difference(-3, 2, house_size, house_price)4.12 (실습) 선형 회귀 경사 하강법 구현하기

gradient_descent 함수
함수 gradient_descent는 실제 경사 하강법을 구현하는 함수입니다. 파라미터로는 임의의 값을 갖는 파라미터들 theta_0, theta_1, 입력 변수 x, 목표 변수 y, 경사 하강법을 몇 번을 하는지를 나타내는 변수 iterations, 그리고 학습률 alpha를 갖습니다.
처음에 gradient_descent 함수에 넘겨주는 theta_0, theta_1 변수들은 0 또는 임의의 값들이고요. gradient_descent 함수는 경사 하강법을 이용해서 최적의 theta_0, theta_1 값들을 찾아서 리턴합니다.
numpy 배열 원소들 평균
numpy 배열에 mean() 메소드를 사용하면 안에 들어 있는 원소들의 평균을 쉽게 구할 수 있습니다.
np_array = np.array([1, 2, 3, 4, 5])
np_array.mean() # 3code
import numpy as np
def prediction(theta_0, theta_1, x):
return theta_0 + theta_1 * x
def prediction_difference(theta_0, theta_1, x, y):
"""모든 예측 값들과 목표 변수들의 오차를 벡터로 리턴해주는 함수"""
return prediction(theta_0, theta_1, x) - y
def gradient_descent(theta_0, theta_1, x, y, iterations, alpha):
"""주어진 theta_0, theta_1 변수들을 경사 하강를 하면서 업데이트 해주는 함수"""
for _ in range(iterations): # 정해진 번만큼 경사 하강을 한다
error = prediction_difference(theta_0, theta_1, x, y) # 예측값들과 입력 변수들의 오차를 계산
theta_0 = theta_0 - alpha * error.mean()
theta_1 = theta_1 - alpha * (error * x).mean()
# 원소별 곱하기이기 때문에 error * x 를 쓴다
return theta_0, theta_1
# 입력 변수(집 크기) 초기화 (모든 집 평수 데이터를 1/10 크기로 줄임)
house_size = np.array([0.9, 1.4, 2, 2.1, 2.6, 3.3, 3.35, 3.9, 4.4, 4.7, 5.2, 5.75, 6.7, 6.9])
# 목표 변수(집 가격) 초기화 (모든 집 값 데이터를 1/10 크기로 줄임)
house_price = np.array([0.3, 0.75, 0.45, 1.1, 1.45, 0.9, 1.8, 0.9, 1.5, 2.2, 1.75, 2.3, 2.49, 2.6])
# theta 값들 초기화 (아무 값이나 시작함)
theta_0 = 2.5
theta_1 = 0
# 학습률 0.1로 200번 경사 하강
theta_0, theta_1 = gradient_descent(theta_0, theta_1, house_size, house_price, 200, 0.1)
theta_0, theta_14.13 경사 하강법 구현 시각화
import numpy as np
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.pyplot as plt
def prediction(theta_0, theta_1, x):
return theta_0 + theta_1 * x
def prediction_difference(theta_0, theta_1, x, y):
return prediction(theta_0, theta_1, x) - y
def gradient_descent(theta_0, theta_1, x, y, iterations, alpha):
m = len(x) #총 데이터 개수
cost_list = [] # 손실을 저장하는 리스트 (경사하강을 할 때마다의 손실을 저장)
"""주어진 theta_0, theta_1 변수들을 경사 하강를 하면서 업데이트 해주는 함수"""
for i in range(iterations): # 정해진 번만큼 경사 하강을 한다
error = prediction_difference(theta_0, theta_1, x, y) # 예측값들과 입력 변수들의 오차를 계산
cost = (error @ error) / (2*m) # 손실 계산
cost_list.append(cost) # 손실 저장
theta_0 = theta_0 - alpha * error.mean()
theta_1 = theta_1 - alpha * (error * x).mean()
# 원소별 곱하기이기 때문에 error * x 를 쓴다
if i % 10 == 1: # 그래프를 200개 띄우는 건 좀 그러니 10번에 한번 나오게 함
plt.scatter(house_size, house_price) # 선점도 그리기
plt.plot(house_size, prediction(theta_0, theta_1, x), color = 'red') # 가설함수 그리기
plt.show() # 그래프 띄우기
return theta_0, theta_1, cost_listhouse_size = np.array([0.9, 1.4, 2, 2.1, 2.6, 3.3, 3.35, 3.9, 4.4, 4.7, 5.2, 5.75, 6.7, 6.9])
house_price = np.array([0.3, 0.75, 0.45, 1.1, 1.45, 0.9, 1.8, 0.9, 1.5, 2.2, 1.75, 2.3, 2.49, 2.6])
th_0 = 2.5
th_1 = 0th_0, th_1, cost_list = gradient_descent(th_0, th_1, house_size, house_price, 200, 0.1)output
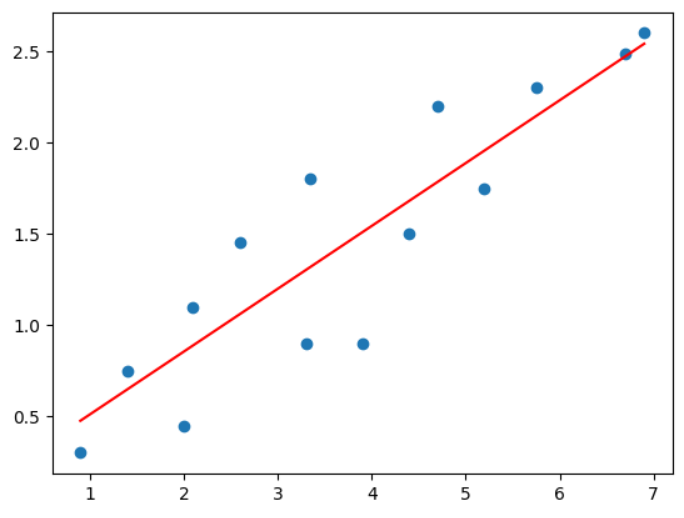
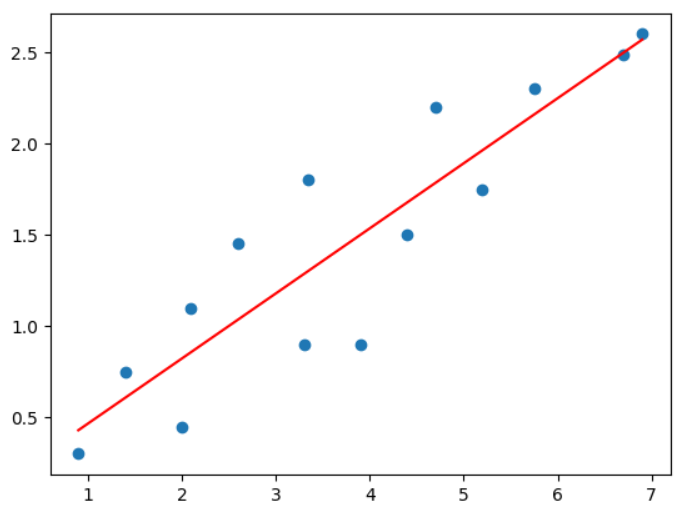
ㄴ 경사하강을 반복하면서 점점 선이 데이터와 연관되어지는 것을 볼 수 있다
print(th_0, th_1)plt.plot(cost_list) #경사 하강을 반복 할수록 손실이 줄어든다output
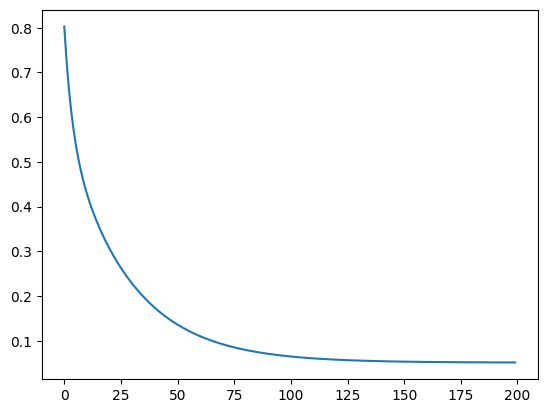
4.14 학습률 알파
경사 하강법을 하기 위해서는 θ0,θ1를
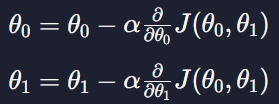
이 식처럼 계속 업데이트 하면 된다
여기서 알파가 학습률인데 이는 경사를 내려갈 때마다 얼마나 많이 그 방향으로 갈 건지를 결정하는 변수이다
학습률 알파를 잘 못 고를 때 생기는 문제점을 알아보고자 함
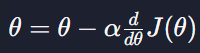
손실함수 J가 하나의 변수 θ로만 이루어졌다고 가정
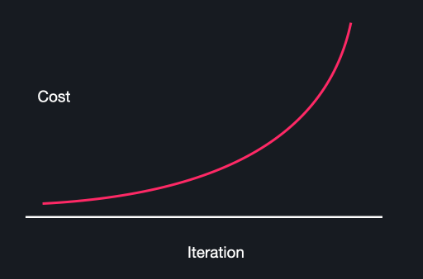
학습률 알파가 너무 큰 경우
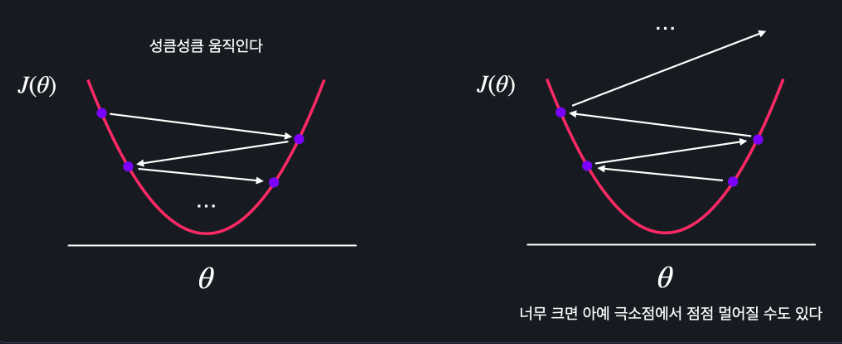
알파가 크면 클수록 경사하강을 할 때마다 θ의 값이 많이 바뀌게 돼서 알파가 너무 크면 경사 하강법을 진행할수록 손실함수 J의 최소점에서 멀어질 수 있다
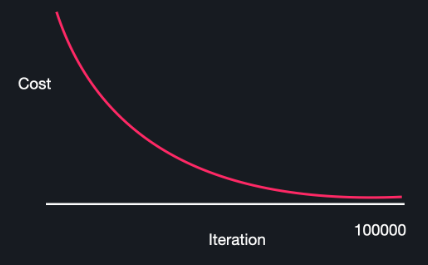
학습률 알파가 너무 작은 경우
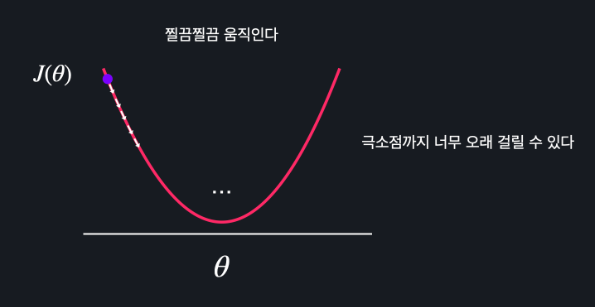
알파가 작으면 θ가 엄청 찔끔찔끔 움직이는데 이러면 최소 지점을 찾는 데에 시간이 너무 오래 걸리게 된다
적절한 학습률
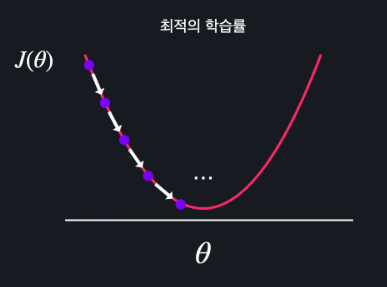
학습률이 너무 클 때에 경사하강법을 한 손실 그래프
작을 때는 iteration 수가 너무 많아짐
그래서 일반적으로 1.0 ~ 0.0 사이의 숫자로 정하고 실험을 통해 경사 하강을 제일 적게 하면서 손실이 잘 줄어드는 학습률을 선택해야한다
4.15 모델 평가하기
가설함수를 수학적으로 표현한다는 의미에서 모델이라고 부른다
데이터를 통해 모델을 개선시키는 것 = 모델을 학습시킨다
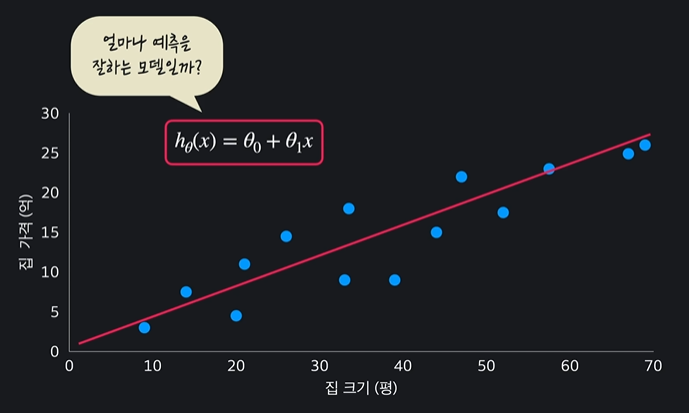
얼마나 결과를 정확히 예측할 수 있을지가 궁금한데 이걸
평균 제곱근 오차를 사용해서 판단할 수 있다
ㄴ = 평균 제곱 오차에 루트를 씌워주는 것
평균 제곱 오차는 제곱이 들어가있으므로 해석하기 힘들기 때문에 평균 제곱근 오차에서 루트를 씌워주는 것이다
우리는 이 데이터에 맞게 학습시켰기 때문에 평균 제곱오차가 낮을 수 밖에 없다
ㄴ 그럼 어떻게 신빙성 있게 모델을 평가할 수 있을까?
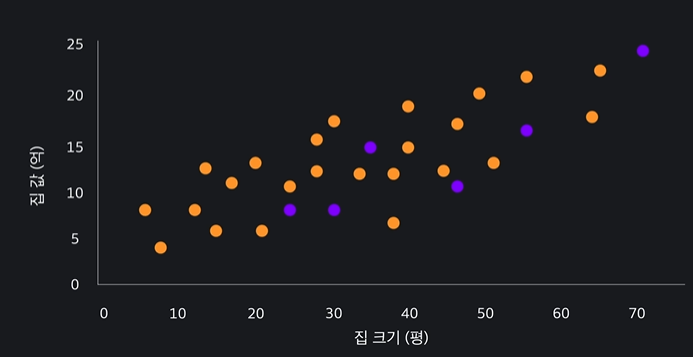
- 학습 (training set)과 평가 (test set) 를 위한 데이터를 나눈다
과정
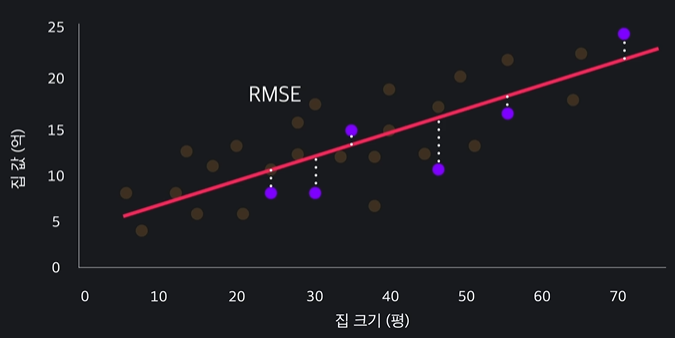
학습데이터로 모델을 학습 시키고 최적선을 구함 -> 평가 데이터만 보고 평가를 한다 !
4.16 scikit-learn 소개 및 데이터 준비
인공지능과 관련된 좋은 라이브러리인 sklearn1이라는 것이 있다 ㅏ!
불러오는 방법
from sklearn.datasets import fetch_california_housing이 라이브러리 안에 있는 데이터를 이용해볼 예정이다.
from sklearn.datasets import fetch_california_housing
import pandas as pd
cal_dataset = fetch_california_housing()
print(cal_dataset.DESCR)output
.. _california_housing_dataset:
California Housing dataset
--------------------------
**Data Set Characteristics:**
:Number of Instances: 20640
:Number of Attributes: 8 numeric, predictive attributes and the target
:Attribute Information:
- MedInc median income in block group
- HouseAge median house age in block group
- AveRooms average number of rooms per household
- AveBedrms average number of bedrooms per household
- Population block group population
- AveOccup average number of household members
- Latitude block group latitude
- Longitude block group longitude
:Missing Attribute Values: None
This dataset was obtained from the StatLib repository.
https://www.dcc.fc.up.pt/~ltorgo/Regression/cal_housing.html
The target variable is the median house value for California districts,
expressed in hundreds of thousands of dollars ($100,000).
This dataset was derived from the 1990 U.S. census, using one row per census
block group. A block group is the smallest geographical unit for which the U.S.
Census Bureau publishes sample data (a block group typically has a population
of 600 to 3,000 people).
A household is a group of people residing within a home. Since the average
number of rooms and bedrooms in this dataset are provided per household, these
columns may take surprisingly large values for block groups with few households
and many empty houses, such as vacation resorts.
It can be downloaded/loaded using the
:func:`sklearn.datasets.fetch_california_housing` function.
.. topic:: References
- Pace, R. Kelley and Ronald Barry, Sparse Spatial Autoregressions,
Statistics and Probability Letters, 33 (1997) 291-297이렇게 안에 있는 데이터들과 설명들이 나온다
속성 이름들 (column) 나오게 하려면 .feature_names를 사용하자
cal_dataset.feature_names # 속성 이름들이 나옴output
['MedInc',
'HouseAge',
'AveRooms',
'AveBedrms',
'Population',
'AveOccup',
'Latitude',
'Longitude']입력 변수들이 행렬로 나오게 하는 법은 .data
cal_dataset.data # 입력 변수들이 행렬로 나옴output
array([[ 8.3252 , 41. , 6.98412698, ..., 2.55555556,
37.88 , -122.23 ],
[ 8.3014 , 21. , 6.23813708, ..., 2.10984183,
37.86 , -122.22 ],
[ 7.2574 , 52. , 8.28813559, ..., 2.80225989,
37.85 , -122.24 ],
...,
[ 1.7 , 17. , 5.20554273, ..., 2.3256351 ,
39.43 , -121.22 ],
[ 1.8672 , 18. , 5.32951289, ..., 2.12320917,
39.43 , -121.32 ],
[ 2.3886 , 16. , 5.25471698, ..., 2.61698113,
39.37 , -121.24 ]])이 행렬의 모양을 보려면 .shape 이용
cal_dataset.data.shape # 행렬 모양 보기output
(20640, 8)목표 변수가 나오게 하려면 .target을 이용하기
cal_dataset.target # 목표 변수가 나옴output
array([4.526, 3.585, 3.521, ..., 0.923, 0.847, 0.894])그리고 이 목표변수의 행렬 모양을 다시 봐보면
cal_dataset.target.shapeoutput
(20640,)위에꺼는 다 numpy였는데 dataframe을 사용하기 위해 pandas로도 해보자
x = pd.DataFrame(cal_dataset.data, columns = cal_dataset.feature_names)
xoutput

이번 강에서는 입력 변수가 하나인 경우만 보기로 했다
x = x[["MedInc"]] # 입력 변수가 하나인 경우만 보기 때문
x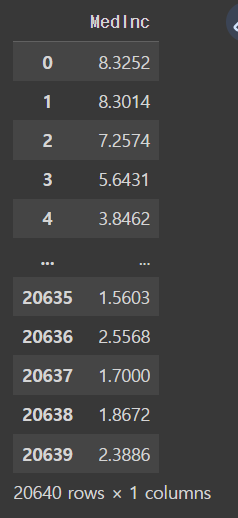
output
y = pd.DataFrame(cal_dataset.target, columns = ['HouseAge'])
youtput
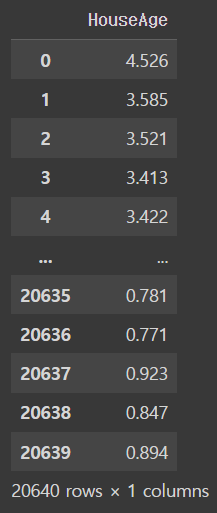
이렇게 데이터 준비는 끝났당 ~~
4.17 scikit-learn 데이터 셋 나누기
from sklearn.model_selection import train_test_split
ㄴ training set과 test set 으로 나눠주는 라이브러리
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size = 0.2, random_state=5)train_test_split()안에 test_size 는 전테 뎅터 중에 testsize를 20%로 설정해서 training set을 80%가 되게 해주는 뜻
random state 는 그 20%를 어떻게 고를지 정하는 뜻 이건 optional parameter라서 굳이 안적어줘도 돌아가긴 한다.
print(x_train.shape)
print(x_test.shape)
print(y_train.shape)
print(y_test.shape)output
(16512, 1)
(4128, 1)
(16512, 1)
(4128, 1)ㄴ 이렇게 나오는 이유 !!는 20:80으로 나눠줬기 때문
여기서도 보면 4128 x 4 = 16512 인게 나타난다
4.18 scikit-learn으로 선형 회귀 쉽게 하기
from sklearn.linear_model import LinearRegression선형회귀 모델을 import 해와야 한다 !
그리고 우리는 평균 제곱근 오차를 구할 것이기 때문에
from sklearn.metrics import mean_squared_error이 역시 import 해준다
model = LinearRegression()선형회귀 함수를 불러와서 model변수에 넣어준다
그 후에 .fit()을 사용하고 매개변수로 training set들을 넣어주어서 모델을 학습시켜줍니다
model.fit(x_train, y_train)output
.coef_는 학습된 선형 회귀 모델의 계수(coefficients)를 나타내는 속성이다. 우리는 여기서 theta 1 값을 구할 수 있다
model.coef_ouput
array([[0.41715893]]).intercept_는 선형 회귀 모델의 절편(intercept)를 나타내는 속성임 ! 우리는 theta 0의 값을 알 수 있음
model.intercept_output
array([0.45036681])출력값들을 보고 우리는 f(x) = 0.45036681 - 0.41715893x 라는 최적선을 구했다
test set에 대한 예측값들
y_test_prediction = model.predict(x_test) # test set에 대한 예측값들
y_test_predictionoutput
array([[1.59175535],
[1.95656084],
[1.33682953],
...,
[1.65165938],
[1.70735009],
[1.30099558]])평균 제곱 오차는 mean_squared_error()함수로 구한다
mean_squared_error(y_test, y_test_prediction) #평균 제곱 오차output
0.7106636941251759근데 우리는 평균 제곱근 오차가 구하고 싶기 때문에 루트를 씌워주는 ** 0.5를 써준다
mean_squared_error(y_test, y_test_prediction) ** 0.5 # 평균 제곱근 오차output
0.84300871533168394.19 (실습) 범죄율로 집 값 예측하기
이번 챕터에서는 선형 회귀 이론과 구현, 그리고 scikit-learn 라이브러리를 사용해서 쉽게 사용하는 법까지 배웠는데요. 이번 과제에서는 scikit-learn을 사용해서 선형 회귀를 직접 연습해 볼게요.
전 레슨에서는 집의 나이 AGE 열을 가지고 와서 선형 회귀를 적용했었는데요. 이번 과제에서는 한번 동네의 범죄율, CRIM을 사용해서 선형 회귀를 해보도록 하겠습니다.
sci-kit learn 라이브러리에서 데이터를 가져 오고, 각각 입력 변수와 목표 변수를 pandas Dataframe으로 변환하는 부분까지의 코드는 작성해 놓았는데요.
이후, 다음 내용을 직접 작성해 보세요.
- 범죄율 열을 선택
- training-test set 나누기
- 모델을 학습
- test 데이터로 예측
조건
- 입력 변수로는 범죄율 열만 이용하세요.
- train_test_split 함수의 옵셔널 파라미터는 test_size=0.2, random_state=5 이렇게 설정해주세요.
- 예측 값 벡터 변수 이름은 꼭 y_test_predict를 쓰세요!
- 정답 확인은 모델의 성능으로 합니다. (템플렛 가장 아래 줄에 출력 코드 있음)
code
# 필요한 라이브러리 import
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import pandas as pd
# 보스턴 집 데이터 갖고 오기
boston_house_dataset = datasets.load_boston()
# 입력 변수를 사용하기 편하게 pandas dataframe으로 변환
X = pd.DataFrame(boston_house_dataset.data, columns=boston_house_dataset.feature_names)
# 목표 변수를 사용하기 편하게 pandas dataframe으로 변환
y = pd.DataFrame(boston_house_dataset.target, columns=['MEDV'])
# 여기에 코드를 작성하세요
x = X[['CRIM']] # 데이터에서 범죄율 열만 선택
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size = 0.2, random_state = 5) # x에는 입력변수(범죄율 데이터) y에는 목표변수(집값)이 저장되어있음
model = LinearRegression() # 데이터로 모델을 학습시켜야 돼서 모델을 갖고와줌
model.fit(x_train, y_train) # training set 데이터만 이용해서 학습 시키기
y_test_predict = model.predict(x_test)
# 테스트 코드 (평균 제곱근 오차로 모델 성능 평가)
mse = mean_squared_error(y_test, y_test_predict)
mse ** 0.5