다중 선형 회귀

5.1 다중 선형 회귀

선형회귀 : 입력변수 1개 --(예측)--> 목표변수

여러 입력변수를 사용하는게 다중 선형 회귀이다

• 다중 선형 회귀는 시각적으로 표현하기 힘들다
  ㄴ 하지만 개념은 똑같다 !!

---

5.2 다중 선형 회귀 표현법

입력변수를 속성이라고 한다

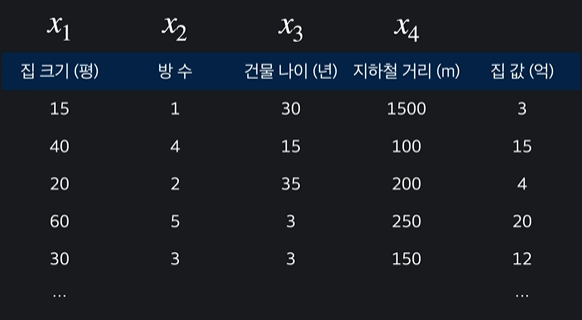
이 표에서는 속성이 4개여서 n=4라고 한다
그리고 입력변수는 4개이지만 목표변수는 하나이다 y라고 나타냄 !

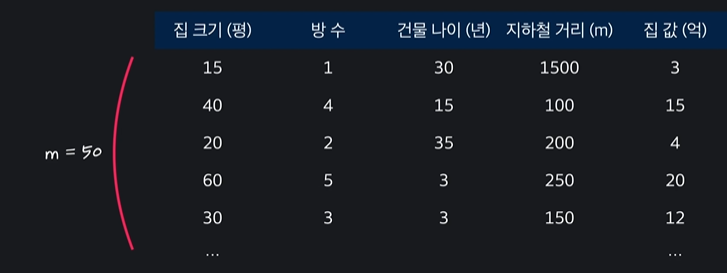
학습데이터의 개수는 m이라고 한다

첫번째 집의 입력변수는

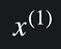
로 표현하고
첫번째 집의 목표변수는

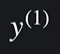
로 표현한다

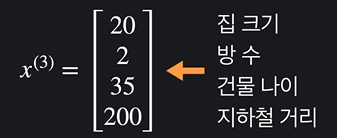
그리고 이는 벡터이다 !!

그럼 만약에 3번째 집의 속성 중 방수를 나타내고 싶으면 어떻게 해야할까?

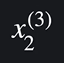
이렇게 표현하고 이걸 일반화 하면

로 쓴다

---

5.3 다중 선형 회귀 가설 함수

가설함수 복습 !

입력 변수가 하나였을 때)

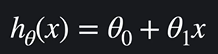
가설함수는 입력변수를 받으면 목표변수를 예측해준다
ex) 집 크기 --(예측)--> 집 값

다중 선형 회귀의 가설함수는

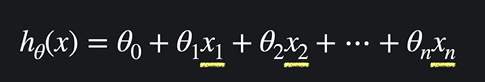
이렇게 생겼고 입력변수가 여러개이다. 복잡해보이지만 일차항이다 ~~

이렇게 볼 수 있다

그리고 세타들은

이렇게 영향력이라고 볼 수 있고 결과값인 가설함수는 집 값이다.

다중 선형 회귀에서 목적은 세타값들을 조금씩 조율하면서 최적의 값들을 구하는 것이다 !!

이를 벡터를 사용해서

이렇게 다시 쓸 수 있다

---

5.4 다중 선형 회귀 경사 하강법

가설 함수가 얼마나 좋은지 평가해야하는데 이를 손실함수로 평가한다

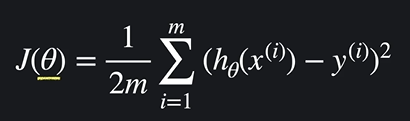
• 손실함수가 크면 -> 가설 함수가 데이터에 잘 안맞는다
• 손실함수가 작으면 -> 가설 함수가 데이터에 잘 맞는다

경사하강법 : 손실을 가장 빨리 줄이는 방향으로 세타 값들을 바꿔주는 방법

그럼 다중선형회귀에서는 어떻게 할 수 있을까?

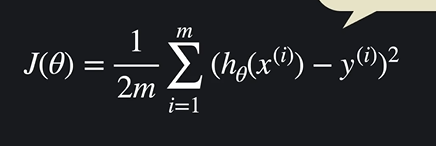
다중 선형회귀에서도 손실함수는 똑같다

입력변수가 하나일 때 경사하강법 )

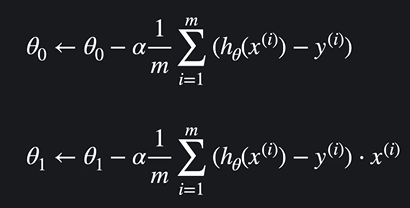
입력변수가 여러개일 때 경사하강법 )

이렇게 나열 되어있는걸 한 줄로 일반화시키면

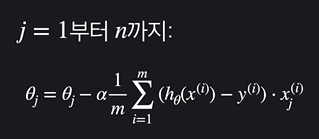
로 볼 수 있다

---

5.5 다중 선형 회귀 구현하기 쉽게 표현하기

입력 변수와 파라미터 표현

다중 선형회귀에서 속성을 벡터로 표현할 때는

이렇게 표현 ! 오른쪽 위의 숫자는 몇번째 데이터인지, 오른쪽 아래 숫자는 몇번째 속성인지를 나타냄

다중선형회귀에서는 가설함수를

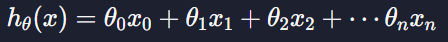
가상의 0번째 속성 x0을 만들고 값을 항상 1로 설정해주어서 표현한다 !

세타 값들도 두개에서 그 이상으로 넘어갈 때에는 벡터로 표현함

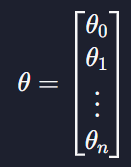
모든 데이터 예측 값

가설함수를 행렬 연산에서 어떻게 표현하는지 !

우선 입력변수와 파라미터를

이렇게 표현함

그 다음 모든 데이터의 예측값은 두 행렬의 곱으로 나타낼 수 있다

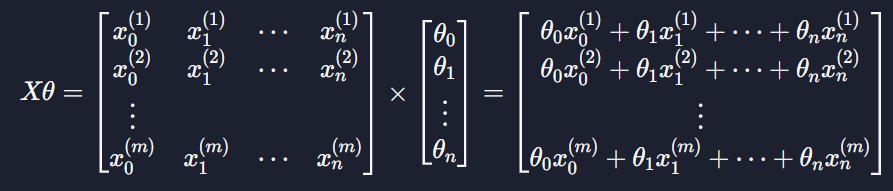
예측 오차

목표변수는 다중선형회귀여도 하나이기 때문에

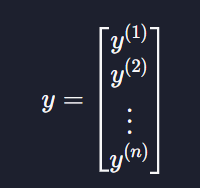
로 표현한다

Xθ에서 y를 빼면

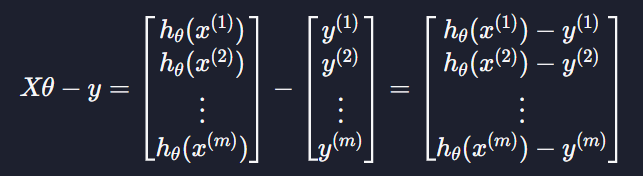
로 표현이 가능하고 이를 error라고 부른다 ~~

경사 하강법

다중 선형 회귀에서 θ값 업데이트는

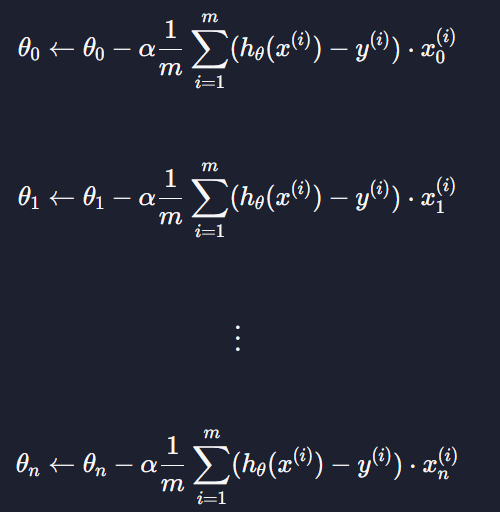
이렇게 하는데 이를 행렬 연산을 사용해서 짧게 표현이 가능하다 !!

행렬연산은

이거고 이 결과값이

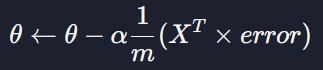
이와 같은 짧은 식이 나온다
그리고

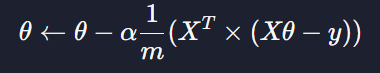
이것 또한 같다

5.6 다중 선형 회귀 가설 함수 구현하기

이번 레슨에서는 다중 선형 회귀의 가정 함수를 prediction 함수로 구현해보겠습니다.

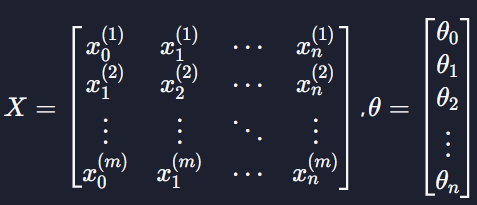
라고 할 때, 모든 학습 데이터에 대한 예측 값들을 그냥 간단하게 Xθ로 나타낼 수 있다고 했잖아요? 이 부분을 구현하면 되는 거죠.

가정 함수 prediction은 파라미터로 입력 변수 X를 나타내는 X 그리고, 파라미터 θ를 나타내는 theta를 받습니다. 이 두 파라미터를 갖고 모든 데이터의 예측 값을 numpy 배열로 리턴하는 함수 prediction을 구현해보세요!

code

import numpy as np

def prediction(X, theta):
    f = X @ theta
    return f
    
# 입력 변수
house_size = np.array([1.0, 1.5, 1.8, 5, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0, 6.0, 7.0, 8.0, 8.5, 9.0, 10.0])  # 집 크기
distance_from_station = np.array([5, 4.6, 4.2, 3.9, 3.9, 3.6, 3.5, 3.4, 2.9, 2.8, 2.7, 2.3, 2.0, 1.8, 1.5, 1.0])  # 지하철역으로부터의 거리 (km)
number_of_rooms = np.array([1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4])  # 방 수

# 설계 행렬 X 정의
X = np.array([
    np.ones(16),
    house_size,
    distance_from_station,
    number_of_rooms
]).T

# 파라미터 theta 값 정의
theta = np.array([1, 2, 3, 4])

prediction(X, theta)

---

5.7 다중 선형 회귀 경사 하강법 구현하기

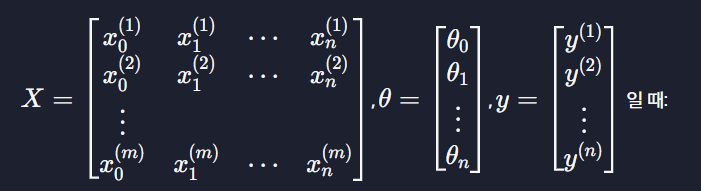
다중 선형 회귀 경사 하강법을 행렬 연산으로

손실함수 J(θ) 최소점을 찾을 때까지(또는 미리 정한 횟수 만큼) :

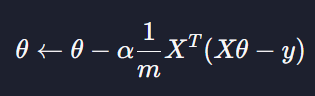
이렇게 표현할 수 있다고 했는데요. 이번 레슨에서는 이 내용을 한번 코드로 구현해 보겠습니다.

gradient_descent 함수
gradient_descent 함수는 경사 하강법을 구현하는 함수입니다. 파라미터로는 설계 행렬 X, 파라미터 theta, 목표 변수 y, 경사 하강법을 실행하는 횟수 iterations, 그리고 학습률 alpha를 받습니다.

iterations번만큼 경사 하강법을 진행하고, 그 결과(theta)를 리턴합니다.

code

import numpy as np

def prediction(X, theta):
    """다중 선형 회귀 가정 함수. 모든 데이터에 대한 예측 값을 numpy 배열로 리턴한다"""
    return X @ theta
    

def gradient_descent(X, theta, y, iterations, alpha):
    """다중 선형 회귀 경사 하강법을 구현한 함수"""
    m = len(X)  # 입력 변수 개수 저장
    
    for _ in range(iterations):
        # 코드를 쓰세요
        error = prediction(X, theta) - y
        theta = theta - alpha / m * (X.T @ error)
        
    return theta

# 입력 변수
house_size = np.array([1.0, 1.5, 1.8, 5, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0, 6.0, 7.0, 8.0, 8.5, 9.0, 10.0])  # 집 크기
distance_from_station = np.array([5, 4.6, 4.2, 3.9, 3.9, 3.6, 3.5, 3.4, 2.9, 2.8, 2.7, 2.3, 2.0, 1.8, 1.5, 1.0])  # 지하철역으로부터의 거리 (km)
number_of_rooms = np.array([1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4])  # 방 수

# 목표 변수
house_price = np.array([3, 3.2, 3.6 , 8, 3.4, 4.5, 5, 5.8, 6, 6.5, 9, 9, 10, 12, 13, 15])  # 집 가격

# 설계 행렬 X 정의
X = np.array([
    np.ones(16),
    house_size,
    distance_from_station,
    number_of_rooms
]).T

# 입력 변수 y 정의
y = house_price

# 파라미터 theta 초기화
theta = np.array([0, 0, 0, 0])

# 학습률 0.01로 100번 경사 하강
theta = gradient_descent(X, theta, y, 100, 0.01)

theta

---

5.8 정규 방정식

극소점을 찾기 위해 경사하강법을 진행하는데 바로 극소점을 찾는 방법은 없을까?

ㄴ 극소점은 기울기가 0이기 때문에 방정식으로 전개해서 풀 수 있다 !!

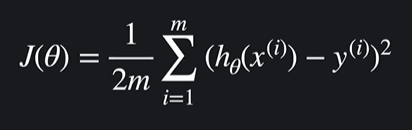
선형 회귀에서 손실함수가 이렇게 생겼는데

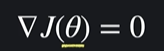
이 기울기가 0이 되는 지점을 방정식을 풀어서 최적의 θ값을 구하면 된다

경사하강법이 아니라 방정식을 통해 극소점을 찾는 방법을 정규 방정식이라고 한다 ~~

---

5.9 (실습) 다중 선형 회귀 정규 방정식 구현하기

이번 과제에서는 정규 방정식을 구현해서 선형 회귀 문제를 해결해보겠습니다.
정규 방정식은 손실 함수 J(θ)의 경사를 0으로 정의해서 (∇J(θ) = 0) J의 최소 지점을 찾는 방법이었는데요.

이렇게 단순 행렬 계산만으로도 최적의 θ값들을 구할 수 있습니다. 이번 과제에서는 numpy를 이용해서 이 식을 한 번 직접 구현해보겠습니다.

normal_equation 함수
normal_equation 함수는 파라미터로 설계 행렬 X, 모든 목표 변수 벡터 y를 받아서 정규 방정식을 계산해 최적의 theta 값들을 numpy 배열로 리턴합니다.

code

import numpy as np

def normal_equation(X, y):
    """설계 행렬 X와 목표 변수 벡터 y를 받아 정규 방정식으로 최적의 theta를 구하는 함수"""
    res = np.linalg.pinv(X.T @ X) @ X.T @ y
    return res
    
# 입력 변수
house_size = np.array([1.0, 1.5, 1.8, 5, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0, 6.0, 7.0, 8.0, 8.5, 9.0, 10.0])  # 집 크기
distance_from_station = np.array([5, 4.6, 4.2, 3.9, 3.9, 3.6, 3.5, 3.4, 2.9, 2.8, 2.7, 2.3, 2.0, 1.8, 1.5, 1.0])  # 지하철역으로부터의 거리 (km)
number_of_rooms = np.array([1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4])  # 방 수

# 목표 변수
house_price = np.array([3, 3.2, 3.6 , 8, 3.4, 4.5, 5, 5.8, 6, 6.5, 9, 9, 10, 12, 13, 15])  # 집 가격

# 입력 변수 파라미터 X 정의
X = np.array([
    np.ones(16),
    house_size,
    distance_from_station,
    number_of_rooms
]).T

# 입력 변수 y 정의
y = house_price

# 정규 방적식으로 theta 계산
theta = normal_equation(X, y)
theta

---

5.10 경사 하강법 vs 정규 방정식

이번 챕터에서는 선형 회귀의 손실 함수 J(θ)를 최소화하는 θ를 찾는 두 가지 방법, 경사 하강법과 정규 방정식을 봤는데요. 이 두 가지 방법을 표로 만들어서 비교해보도록 하겠습니다.

경사 하강법

• 적합한 학습율 α를 찾거나 정해야 한다
• 반복문을 이용해야 한다
• 입력 변수의 개수 n이 커도 효율적으로 연산을 할 수 있다.

정규방정식

• 학습율 α를 정할 필요가 없다
• 한 단계로 계산을 끝낼 수 있다
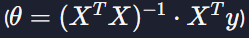
• 입력 변수의 개수 n이 커지면 커질수록 월등히 비효율적이다. (행렬 연산을 하는 비용이 경사 하강법을 하는 것 보다 크다)
• 역행렬이 존재하지 않을 수도 있다

표로 나타내기

이런 차이가 있습니다.

그렇다면 둘 중 어떤 걸 선택해야 되는 걸까요?

절대적으로 정해진 건 없긴한데요. 입력 변수(속성)의 수가 엄청 많을 때는(1000개를 넘느냐를 기준으로 사용할 때가 많습니다) 경사 하강법을, 그리고 비교적 입력 변수의 수가 적을 때는 정규 방정식을 사용합니다.

이번 레슨은 어땠나요?

---

5.11 Convex 함수

저번과 이번 챕터에서는 경사 하강법, 그리고 정규 방정식을 이용해서 선형과 다중 회귀 손실 함수를 최소화시키는 방법을 배웠는데요.

손실 함수 J(θ)의 경사를 구한 뒤에 이걸 이용해서 최솟값을 갖는 θ를 찾았습니다. 근데 단순히 경사 하강법과 정규 방정식만 이용하면 항상 손실 함수의 최소 지점을 찾을 수 있을까요?

이런 함수에서 경사 하강법을 한다고 해볼게요.

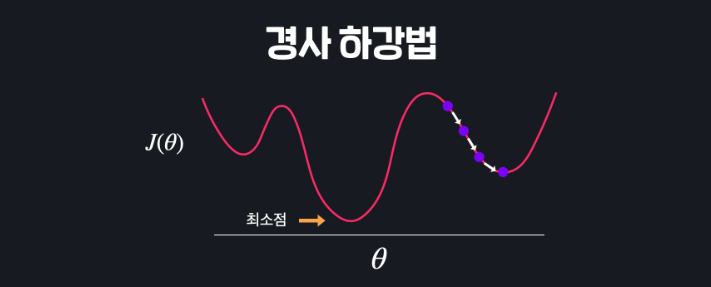
이 지점에서 시작을 해서 경사를 따라 쭉 내려갑니다. 내려가다가 보면 어느 순간 여러 극소값 중 하나에 오겠죠? 그럼 여기서는 경사가 0이어서 경사 하강이 종료가 될 텐데요. 그럼 손실 함수의 최저점을 찾아갈 수가 없습니다.

정규 방정식도 마찬가지입니다.

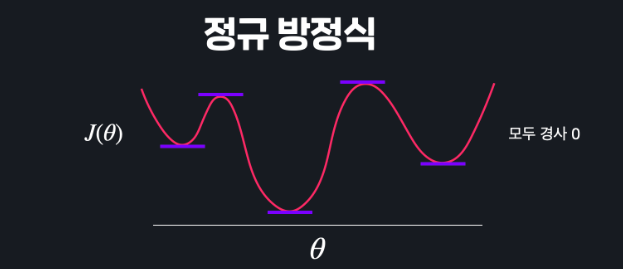
이렇게 수많은 극소값들과 극대값들이 있으면 아무리 방정식을 해결해도 구한 수많은 지점 중에서 어떤 지점이 최소점인지를 알 수가 없죠. 이 모든 지점들이 경사가 0일테니까요.

그러니까 함수가 이런 식으로 생긴 경우에는 경사 하강법과 정규 방정식을 통해서 구한 극소 지점이 손실 함수 전체에서 최소 지점이라고 확실하게 얘기할 수가 없는 건데요.

반대로 손실 함수가 이렇게 생겼다고 합시다.

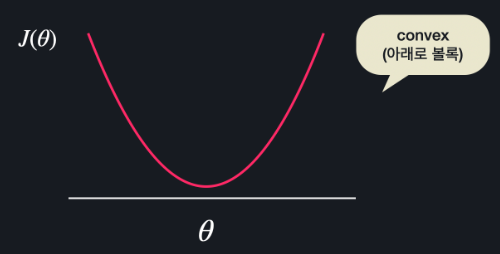
이 함수는 어떤 지점에서 경사 하강을 시작해도 항상 손실 함수의 최소 지점을 찾을 수 있고, 정규 방정식을 이용해서 최소점을 구할 수 있겠죠?

이런 함수를 convex 함수(아래로 볼록한 함수)라고 부릅니다.

convex 함수에서는 항상 경사 하강법이나 정규 방정식을 이용해서 최소점을 구할 수 있는 반면, 노트 위에서 봤던 non-convex 함수에서는 구한 극소점이 최소점이라고 확신할 수 없죠.

선형 회귀의 평균 제곱 오차

선형 회귀에서는 가정 함수의 예측값들과 실제 목표 변수들의 평균 제곱 오차(MSE)를 손실 함수로 사용했는데요. 다행히 선형 회귀 손실 함수로 사용하는 MSE는 항상 convex 함수입니다. 그러니까 선형 회귀를 할 때는 경사 하강법을 하거나 정규 방정식을 하거나 항상 최적의 θ값들을 구할 수 있는 거죠.

---

5.12 scikit-learn 데이터 준비

from sklearn.datasets import fetch_california_housing
import pandas as pd

cal_dataset = fetch_california_housing()

cal_dataset.feature_names

output

['MedInc',
 'HouseAge',
 'AveRooms',
 'AveBedrms',
 'Population',
 'AveOccup',
 'Latitude',
 'Longitude']

cal_dataset.data

numpy를 dataframe으로 바꾸고자 !!

X = pd.DataFrame(cal_dataset.data, columns = cal_dataset.feature_names)
X

output

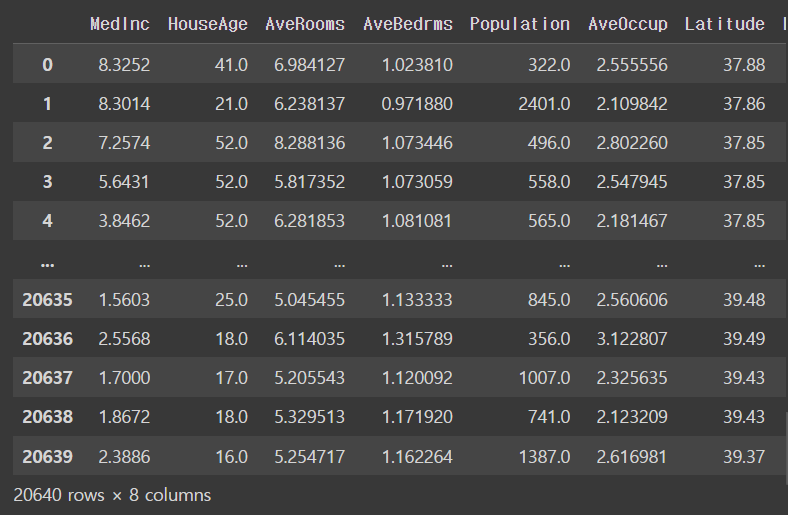
목표변수는 .target으로 정하기

cal_dataset.target

output

array([4.526, 3.585, 3.521, ..., 0.923, 0.847, 0.894])

이거 역시 dataframe으로 하기 위해서

y = pd.DataFrame(cal_dataset.target, columns = ['Longitude'])
y

output

---

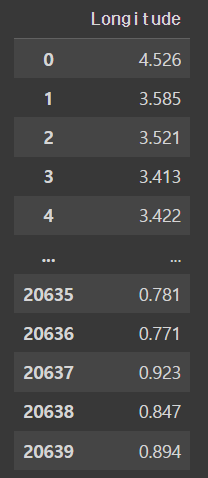
5.13 scikit-learn으로 다중 선형 회귀 쉽게 하기

test set 과 training set을 나누고 변수 입력을 해준다

X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.2, random_state = 5)

어떻게 생겼는지 보기 위해 .shape 씀

print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

output

(16512, 8)
(4128, 8)
(16512, 1)
(4128, 1)

선형회귀를 쓰기 위해 변수에 넣어줌

model = LinearRegression()

training set 을 학습시키기 위해 .fit사용

model.fit(X_train, y_train)

output

세타 1 ~~ 끝 을 벡터에 넣어주는거

model.coef_ # 세타값들이 들어있는거

output

array([[ 4.38384807e-01,  9.17273492e-03, -1.11793600e-01,
         6.79331516e-01, -3.04158117e-06, -4.12179113e-03,
        -4.19560244e-01, -4.33473567e-01]])

세타 0만 넣은거

model.intercept_ # 세타 0은 여기 들어있음

output

array([-36.89554297])

이제 test set을 예측 값으로 만들기 위해 .predict()를 사용

y_test_prediction = model.predict(X_test) # test set 데이터들 !
y_test_prediction

output

array([[1.69422277],
       [1.94022419],
       [1.00866627],
       ...,
       [2.0254698 ],
       [2.07781354],
       [1.06749589]])

마지막으루 평균 제곱근 오차 구하기 !!

mean_squared_error(y_test, y_test_prediction) ** 0.5 # 평균 제곱근 오차

output

0.7323542382277796

---

5.14 scikit-learn으로 당뇨 수치 예측하기

이번 과제에서는 scikit-learn 라이브러리에 있는 또 다른 데이터 셋인 당뇨병 수치 데이터를 이용해서 선형 모델을 학습시켜 보겠습니다.

당뇨병 데이터 셋을 가지고 와서 각각 입력 변수와 목표 변수를 dataframe으로 바꾸는 코드까지는 이미 작성돼 있어요. 앞에서 배운 것처럼 이번 실습에서는 아래 내용들을 작성해 보겠습니다.

1. 데이터를 training/test 셋으로 나누기
2. 선형 회귀 모델을 학습
3. 학습 데이터를 이용한 예측

(과제를 하기 전 꼭 print(diabetes_dataset.DESCR)을 써서 데이터 셋 내용을 살펴보세요!)

조건

• train_test_split 함수의 옵셔널 파라미터는 test_size=0.2, random_state=5 이렇게 설정해 주세요.
• testing set의 예측 값들은 꼭 변수 y_test_predict에 저장해 주세요.
• 정답 확인은 모델의 성능으로 합니다. (템플렛 가장 아래 줄에 출력 코드 있음)

code

# 필요한 라이브러리 import
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

import pandas as pd  

# 당뇨병 데이터 갖고 오기
diabetes_dataset = datasets.load_diabetes()

# 입력 변수를 사용하기 편하게 pandas dataframe으로 변환
X = pd.DataFrame(diabetes_dataset.data, columns=diabetes_dataset.feature_names)

# 목표 변수를 사용하기 편하게 pandas dataframe으로 변환
y = pd.DataFrame(diabetes_dataset.target, columns=['diabetes'])

# train_test_split를 사용해서 주어진 데이터를 학습, 테스트 데이터로 나눈다
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.2, random_state = 5)

model = LinearRegression() # 선형 회귀 모델을 가지고 오고 
model.fit(X_train, y_train)  # 학습 데이터를 이용해서 모델을 학습 시킨다

y_test_predict = model.predict(X_test)  # 학습시킨 모델로 예측

# 평균 제곱 오차의 루트를 통해서 테스트 데이터에서의 모델 성능 판단
mse = mean_squared_error(y_test, y_test_predict)

mse ** 0.5