다항 회귀

6.1 다항 회귀

데이터들에 적합한 선이 꼭 직선이 아닐 수도 있다

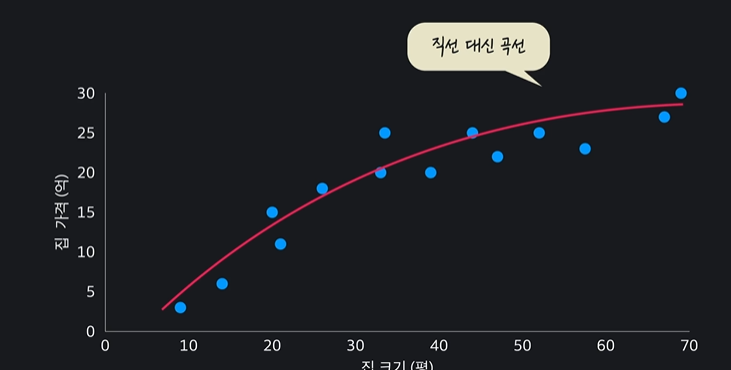
이렇게 ! 곡선일 수도 있다는 것 !!

선형회귀에서 최적선이 직선일 때에 가설함수는

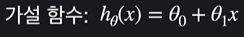
였는데

곡선일 때에는

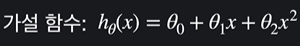
이런식의 2차식으로 쓸 수 있고

삼차함수일 때엔

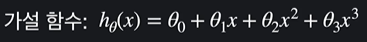
3차식의 가설함수를 써서

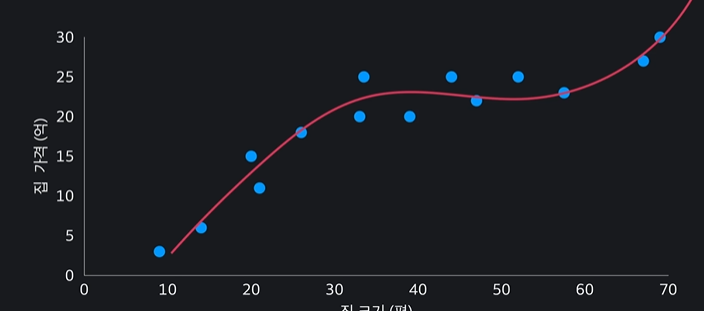
이런 그래프를 나타낼 수 있다

이렇게 데이터에 잘 맞는 다항식이나 곡선을 구해서 학습하는 것을 다항회귀라고 부른다 ~~

---

6.2 단일 속성 다항 회귀

다항 회귀는 속성이 1개인 경우와 속성이 여러개인 경우로 나뉨

• 하나인 경우 !

둘이 아주 비슷하다
첫째줄 : 다항 회귀의 가설함수
둘째줄 : 입력변수가 3개인 다중 선형 회귀의 가설함수

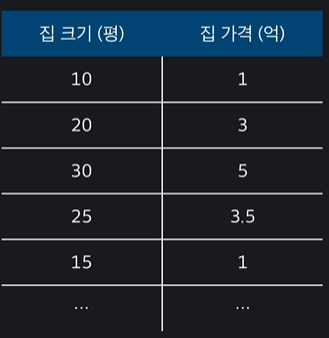
입력 변수인 집크기를 제곱한 값을 열로 만들어서 입력변수를 차항 만큼 늘려서 이 데이터를 갖고 다중 선형 회귀를 하면 된다 ~~

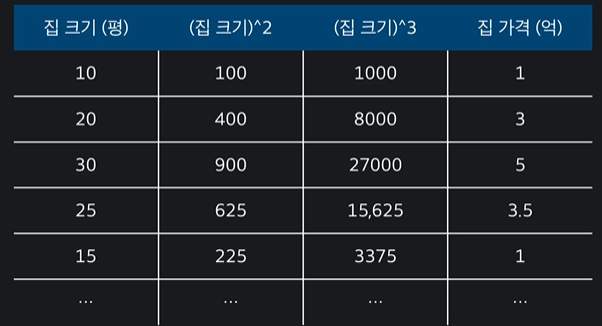
6.3 다중 다항 회귀

다중 다항 회귀는 속성이 여러개인 다항 회귀이다 ~~

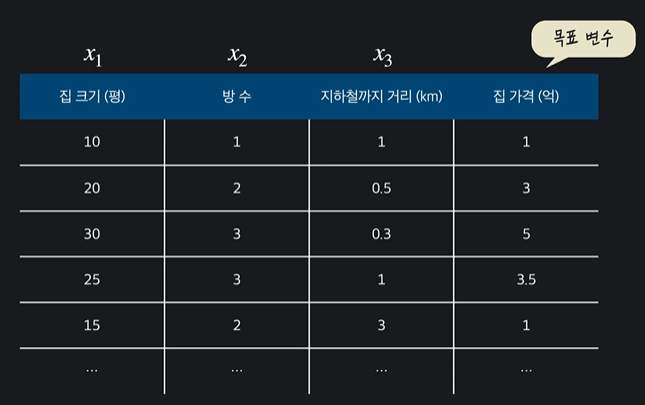
이렇게 속성이 다를 수 이씅ㅁ

가설함수가 2차 함수라고 하면 상수항 + 일차항 + 이차항 이렇게 있음

이를 가상의 열을 추가해줌

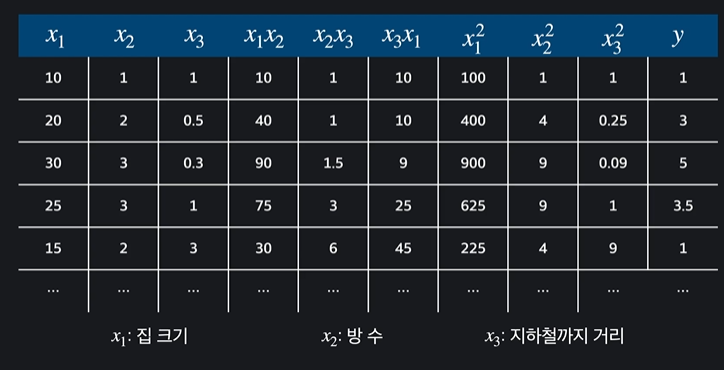
그러면 이제 이 문제를 입력 변수가 9개인 다중 선형 회귀라고 생각할 수 있습니다. 다항 회귀라는 생각을 하지 않고, 그냥 다중 선형 회귀인 것처럼 취급을 하고 문제를 풀면 되는 거죠.

---

6.4 다항 회귀의 힘

다항회귀를 사용하면 단순히 복잡한 고차식에 데이터를 맞추는 것을 넘어서 어떻게 모델의 성능을 극대화할 수 있음

속성 사이의 복잡한 관계

예시를 집 값 예측 문제로 생각해보게씀

집의 크기를 속성으로 이용했는데 이 데이터가 항상 하나만 사용해도 의미가 있는 완벽한 변수일 수는 없다
ex) 집 = 사각형 & 집 크기 대신 집의 높이와 너비 데이터만 있다고 가정

이럴때 아무리 너비가 커도 높이가 작거나, 높이만 크고 너비가 작으면 구조가 비효율적이기 때문에 집값이 안높을 것임
-> 훨씬 더 좋은 수치 = 높이와 너비를 곱한 값 (=집의 넓이)

단순 선형 회귀를 사용하면 두 변수가 독립적이기 때문에 높이와 너비가 같이 커야지만 집 값도 커진다라는 관계를 학습할 수 없음

하지만 속성들을 서로 곱해서 차항을 높여주면, 즉 선형 회귀 문제를 다항 회귀 문제로 만들어주면 속성들 사이에 있을 수 있는 복잡한 관계들을 학습시킬 수 있다 ~

---

6.5 scikit-learn으로 다항 회귀 문제 만들기

모듈들을 불러와줍니다
이번에 새로 나온 다항 속성을 만들어주는 모듈이 있는데 이는
from sklearn.preprocessing import PolynomialFeatures로 불러와주면 된다

from sklearn.datasets import fetch_california_housing
from sklearn.preprocessing import PolynomialFeatures # 다항 속성을 만들어주는 툴

import pandas as pd

데이터 불러오기

cal_dataset = fetch_california_housing()

cal_dataset.data

output

array([[   8.3252    ,   41.        ,    6.98412698, ...,    2.55555556,
          37.88      , -122.23      ],
       [   8.3014    ,   21.        ,    6.23813708, ...,    2.10984183,
          37.86      , -122.22      ],
       [   7.2574    ,   52.        ,    8.28813559, ...,    2.80225989,
          37.85      , -122.24      ],
       ...,
       [   1.7       ,   17.        ,    5.20554273, ...,    2.3256351 ,
          39.43      , -121.22      ],
       [   1.8672    ,   18.        ,    5.32951289, ...,    2.12320917,
          39.43      , -121.32      ],
       [   2.3886    ,   16.        ,    5.25471698, ...,    2.61698113,
          39.37      , -121.24      ]])

어떻게 생겼는지

cal_dataset.data.shape

output

(20640, 8)

속성 이름들은 뭔지 !!

cal_dataset.feature_names

output

['MedInc',
 'HouseAge',
 'AveRooms',
 'AveBedrms',
 'Population',
 'AveOccup',
 'Latitude',
 'Longitude']

이제 데이터를 다항 회귀를 하기 위해 가공해야 한다 !! 그럴 땐 PolynomialFeatures()를 이용하장

polynomial_transformer = PolynomialFeatures(2) 

다항식 변환기인 polynomial_transformer를 사용해서 cal_dataset.data에 포함된 데이터를 다항식 형태의 새로운 데이터로 변환하는 작업을 수행 -> 그 결과 데이터를 polynomial_data에 할당한다 ~~

polynomial_data = polynomial_transformer.fit_transform(diabetes_dataset.data)

그 후에 데이터 확인

polynomial_data

output

array([[ 1.00000000e+00,  8.32520000e+00,  4.10000000e+01, ...,
         1.43489440e+03, -4.63007240e+03,  1.49401729e+04],
       [ 1.00000000e+00,  8.30140000e+00,  2.10000000e+01, ...,
         1.43337960e+03, -4.62724920e+03,  1.49377284e+04],
       [ 1.00000000e+00,  7.25740000e+00,  5.20000000e+01, ...,
         1.43262250e+03, -4.62678400e+03,  1.49426176e+04],
       ...,
       [ 1.00000000e+00,  1.70000000e+00,  1.70000000e+01, ...,
         1.55472490e+03, -4.77970460e+03,  1.46942884e+04],
       [ 1.00000000e+00,  1.86720000e+00,  1.80000000e+01, ...,
         1.55472490e+03, -4.78364760e+03,  1.47185424e+04],
       [ 1.00000000e+00,  2.38860000e+00,  1.60000000e+01, ...,
         1.54999690e+03, -4.77321880e+03,  1.46991376e+04]])

polynomial_data.shape 

output

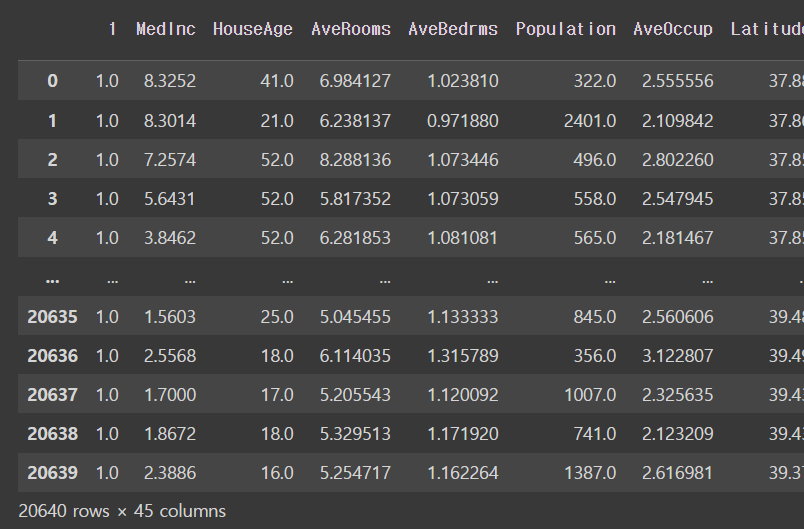
(20640, 45)

아깐 열이 8개 였는데 45개가 된 이유 : 그전의 열을 조합하고 가상의 열 추가해서

polynomial_feature_names = polynomial_transformer.get_feature_names_out(cal_dataset.feature_names)

다항식 변환기인 polynomial_transformer를 사용해서 주어진 데이터셋의 특성 이름에 대응하는 다항식 형태의 특성 이름을 반환하는 작업을 수행 ~~

polynomial_feature_names #가능한 모든 이차 조합이 다 있음

output

array(['1', 'MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population',
       'AveOccup', 'Latitude', 'Longitude', 'MedInc^2', 'MedInc HouseAge',
       'MedInc AveRooms', 'MedInc AveBedrms', 'MedInc Population',
       'MedInc AveOccup', 'MedInc Latitude', 'MedInc Longitude',
       'HouseAge^2', 'HouseAge AveRooms', 'HouseAge AveBedrms',
       'HouseAge Population', 'HouseAge AveOccup', 'HouseAge Latitude',
       'HouseAge Longitude', 'AveRooms^2', 'AveRooms AveBedrms',
       'AveRooms Population', 'AveRooms AveOccup', 'AveRooms Latitude',
       'AveRooms Longitude', 'AveBedrms^2', 'AveBedrms Population',
       'AveBedrms AveOccup', 'AveBedrms Latitude', 'AveBedrms Longitude',
       'Population^2', 'Population AveOccup', 'Population Latitude',
       'Population Longitude', 'AveOccup^2', 'AveOccup Latitude',
       'AveOccup Longitude', 'Latitude^2', 'Latitude Longitude',
       'Longitude^2'], dtype=object)

이거를 이제 데이터프레임으로 !!!

pd.DataFrame(polynomial_data, columns = polynomial_feature_names)

output

---

6.6 scikit-learn으로 다항 회귀 하기

이제 목표변수 !!

cal_dataset.target

output

array([4.526, 3.585, 3.521, ..., 0.923, 0.847, 0.894])

이걸 dataframe 형식으로

y = pd.DataFrame(cal_dataset.target, columns = ['MedInc'])
y

output

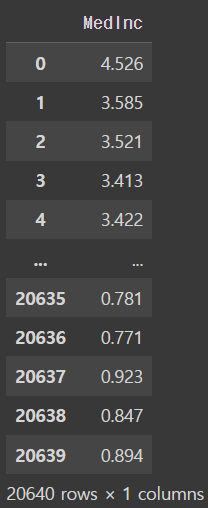
test set과 training set을 변수 저장해준다

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 5)

그리구 선형회귀 모델을 만들어주장

model = LinearRegression()

train set들을 학습시켜준다 ~~

model.fit(X_train, y_train)

output

세타 1~끝 까지의 값

model.coef_

output

array([[-2.80248011e-08, -1.11460579e+01, -8.42046678e-01,
         5.87000335e+00, -3.01542591e+01,  7.20176782e-04,
         1.26283255e+00,  9.33913838e+00,  6.53367998e+00,
        -3.19413706e-02,  1.72899488e-03,  4.79729289e-02,
        -1.95588952e-01,  5.70610752e-05,  1.39122241e-02,
        -1.50452986e-01, -1.42318532e-01,  1.95235463e-04,
        -1.48800352e-03,  1.32187964e-02,  2.07859123e-06,
        -1.48270170e-03, -1.01744841e-02, -9.96935878e-03,
         9.17449054e-03, -8.54938496e-02, -7.22232186e-05,
        -3.05461562e-03,  7.95604098e-02,  7.44834510e-02,
         1.94627546e-01,  4.54000811e-04,  3.79241637e-02,
        -4.20723964e-01, -3.84372526e-01,  1.49691637e-09,
         2.32667180e-05,  2.20900756e-05,  1.62102746e-05,
        -4.48299195e-05,  3.11890742e-02,  2.19467176e-02,
         6.50793940e-02,  1.15401126e-01,  4.37692730e-02]])

세타 0의 값

model.intercept_

output

array([232.6453115])

이제 예측값을 구해보자 !!

y_test_prediction = model.predict(X_test)

output

[[1.52413927]
 [1.99449594]
 [1.22066642]
 ...
 [2.32452997]
 [1.96277818]
 [0.67911811]]

마지막으로 평균 제곱근 오차 구하기

mean_squared_error(y_test, y_test_prediction) ** 0.5

output

1.3135630458302878

---

6.7 다항 회귀로 당뇨병 예측하기 I : 문제 만들기

이번 과제에서는 다항 회귀를 직접 만들어 보겠습니다. 전에 사용했던 당뇨 데이터를 가져오는 부분 코드가 작성돼 있는데요. 데이터를 바꿔서, 당뇨 수치 예측 문제를 2차 다항 문제로 변환해 보세요.

조건

• 2차 다항 회귀 문제로 바꾼 입력 변수 데이터는 변수 X에 pandas dataframe으로 저장해 주세요.
• 데이터 열 이름도 변환한 내용에 맞게 바꿔 주세요.

code

# 필요한 라이브러리 import
from sklearn import datasets
from sklearn.preprocessing import PolynomialFeatures

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

import pandas as pd  

diabetes_dataset = datasets.load_diabetes()  # 데이터 셋 갖고오기

polynomial_transformer = PolynomialFeatures(2) # 2차식 변형기를 정의
polynomial_data = polynomial_transformer.fit_transform(diabetes_dataset.data) # 당뇨 데이터를 2차항 문제로 변환

polynomial_feature_names = polynomial_transformer.get_feature_names(diabetes_dataset.feature_names) # 입력 변수 이름들도 맞게 바꾼다 !!

X = pd.DataFrame(polynomial_data, columns = polynomial_feature_names)

# 테스트 코드
X.head()

---

6.8 다항 회귀로 당뇨병 예측하기 II: 모델 학습하기

저번 과제에서는 당뇨병 데이터를 다항 회귀 문제로 변환했는데요. 이번엔 바꾼 데이터를 사용해서 다항 회귀를 직접 해보겠습니다.

아래 순서대로 진행해 볼게요.

1. 데이터를 training/test set으로 나눈다.
2. 선형 회귀 모델을 가져와서, training set 데이터를 사용해서 학습시킨다.
3. test set 데이터를 이용해서 학습시킨 모델로 예측한다.

조건

• train_test_split 함수의 옵셔널 파라미터는 test_size=0.2, random_state=5 이렇게 설정해 주세요.
• 예측 값 벡터 변수 이름은 꼭 y_test_predict를 사용하세요!
• 정답 확인은 모델의 성능으로 합니다. (템플렛 가장 아래 줄에 출력 코드 있음)

code

# 필요한 라이브러리 import
from sklearn import datasets
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

import pandas as pd  

diabetes_dataset = datasets.load_diabetes()

diabetes_dataset = datasets.load_diabetes()  # 데이터 셋 갖고오기

polynomial_transformer = PolynomialFeatures(2) # 2차식 변형기를 정의
polynomial_data = polynomial_transformer.fit_transform(diabetes_dataset.data) # 당뇨 데이터를 2차항 문제로 변환

polynomial_feature_names = polynomial_transformer.get_feature_names(diabetes_dataset.feature_names) # 입력 변수 이름들도 맞게 바꾼다 !!

X = pd.DataFrame(polynomial_data, columns = polynomial_feature_names)

# 목표 변수
y = pd.DataFrame(diabetes_dataset.target, columns=['diabetes'])

# train_test_split를 사용해서 주어진 데이터를 학습, 테스트 데이터로 나눈다
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 5)

# 선형 회귀 모델을 가지고 오고 
model = LinearRegression()
model.fit(X_train, y_train) # 학습 데이터를 이용해서 모델을 학습 시킨다

# 평균 제곱 오차의 루트를 통해서 테스트 데이터에서의 모델 성능 판단
y_test_predict = model.predict(X_test)

mse = mean_squared_error(y_test, y_test_predict)
mse ** 0.5