
7.1 분류 문제
ex) 어떤 이메일이 스팸인지 아닌지, 아니면 기사가 스포츠 기사인지 정치 기사인지 연예 기사인지.. 를 본다고 가정
보통 분류 문제를 풀 때) 각 결괏값에 어떤 숫자 값을 지정해줌
ex) 이메일이 스팸인지 아닌지 분류할 때
- 이메일엔 0, 스팸에는 1 이런식으로
선형 회귀를 이용한 분류
ex) 공부한 시간을 갖고 시험을 통과할지 예측
- 통과 못하는걸 : 0, 통과 하는걸 1
이걸 가지고 선형회귀를 해서 최적선을 구하면
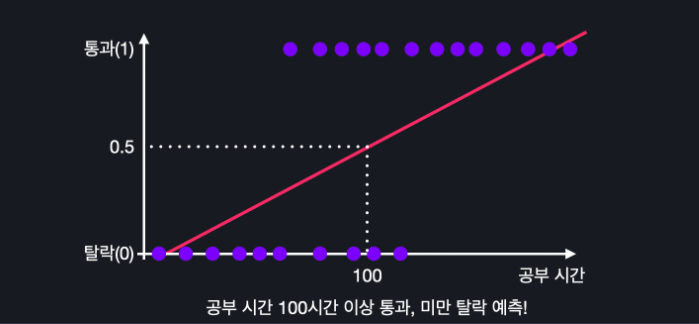
이렇게 최적선이 형성이 되는데 이러면
0.5가 넘는건 통과,0.5가 안되는건 통과 못한 것으로 분류
하지만 우리는 분류 문제를 풀 때에 선형 회귀를 잘 사용하지 않는다. 왜냐?!!
ㄴ ex) 여기에 1000시간을 공부한 데이터 하나 추가
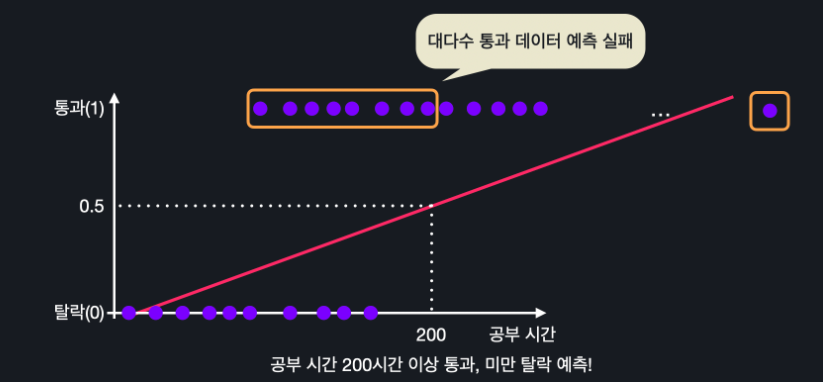
그러면 최적선이 이 데이터 하나로 인해 눕혀지게 된다. 즉, 선형 회귀는 이런 예외적인 데이터에 너무 민감하게 반응하기 때문에 보통 데이터를 분류하고 싶을 때는 잘 사용 X
7.2 로지스틱 회귀
선형회귀일 때 )
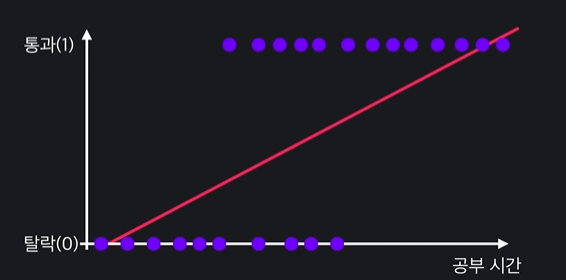
이 데이터에 잘 맞는 일차함수를 찾는 형식
로지스틱 회귀 일 때 )
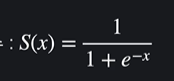
일차함수 말고 시그모이드 함수를 찾음. 시그모이드 함수는 무조건 0~1 사이의 값을 낸다 !!
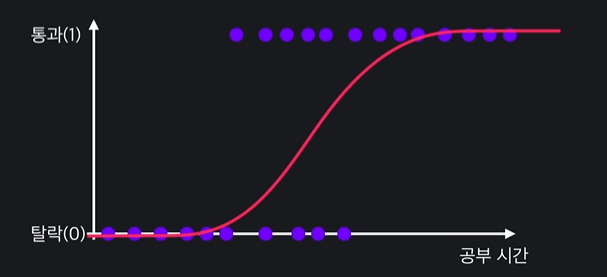
이렇게 생김
선형회귀는 일차함수이기 때문에 결과가 범위 없이 얼마든지 크거나 작아질 수 있다
하지만 시그모이드 함수는 값이 0과 1사이기 때문에 분류에 더 적합!!
7.3 로지스틱 회귀 가설 함수
가설함수 : 입력 변수를 받아서 목표 변수를 예측해주는 함수

ㄴ 선형회귀에서는 이랬음

선형회귀의 가설함수인 gθ(x) = θ^Tx 를 로지스틱 회귀 가설함수에 대입하면 이런 값이 나옴
선형회귀 가설함수는 일차함수이기 때문에 결과값이 엄청 커질수도, 작아질 수도 있는데 이를 로지스틱 회귀 가설함수의 인풋으로 넣으면 무조건 0~1 로 아웃풋이 나온다 ~~
그럼 0과 1사이의 수로 우린 무엇을 할까?
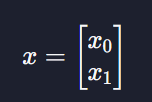
이런 벡터가 있고 가설함수가 하는 일이 공부한 시간을 바탕으로 시험을 통과할지 예측하는거라고 한다면 0은 통과 못하는거, 1은 통과하는 것을 의미
x를 가설함수에 넣었더니 0.9가 나왔다 = 목표 변수가 1일 확률이 0.9 (=90%) 라는 뜻
그러니까 50시간 공부한 학생이 시험을 통과할 확률이 90%라는 뜻 = 이 학생은 통과한 학생으로 분류
하지만 아웃풋이 0.4 라면 통과할 확률이 40%이기 때문에 이 학생은 통과 못한 것으로 분류
7.4 로지스틱 회귀에서 하려는 것
단순화한 시각화
단순화 해서 입력변수가 1개라고 하자
우리는 로지스틱 회귀로
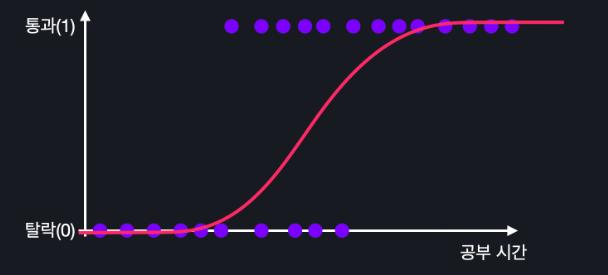
이런 시그모이드 모양의 곡선을 찾아야됨 -> 이 곡선을 어떻게 찾을까? -> θ 값들을 조절해서 찾음 !!
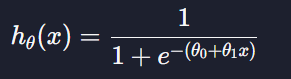
변수가 하나라는건 θ 값이 θ0,θ1로 두개라는 뜻. 이 때 가설함수는 ?
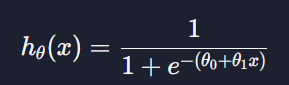
이렇게 표현한다
θ0의 값을 늘리면 곡선이 왼쪽으로, 줄이면 오른쪽으로 움직임
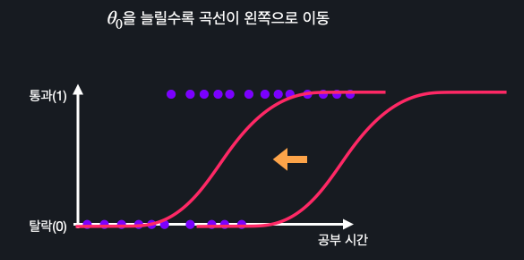
θ1의 값을 늘리면 곡선이 조여지고 줄이면 늘어진다
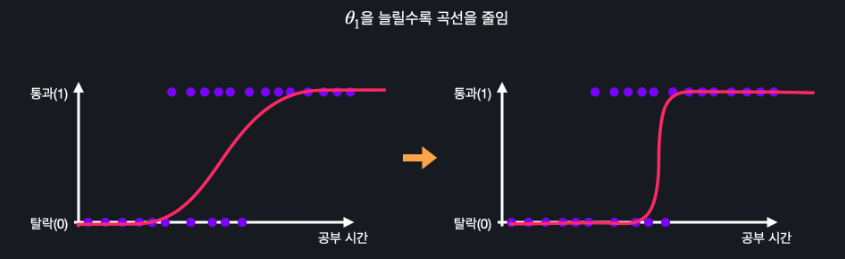
이렇게 θ0,θ1의 값들을 바꿔가면서 갖고 있는 학습 데이터에 잘 맞는 시그모이드 모양의 곡선을 찾아내는 게 로지스틱 회귀의 목적 !!
7.5 결정 경계
속성이 하나일 때
ex) 공부 시간으로 시험을 통과했는지 탈락했는지 예측하고 싶을 때
속성이 하나니까 가설함수가
이렇게 형성됨
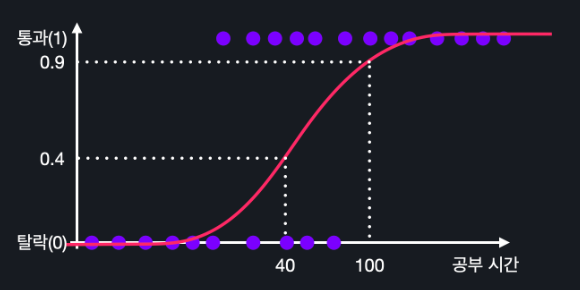
x에 100시간을 넣어서 0.9가 나오면 100시간 공부한 학생이 시험을 통과할 확률은 90%인 것이고 x에 40시간을 넣어서 0.4가 나오면 40시간 공부한 학생이 시험을 통과할 확률은 40%인 것 !!
그렇기 때문에 가설함수의 아웃풋이 0.5인 공부 시간을 알아내면
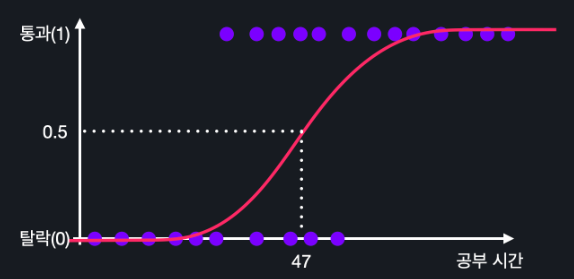
이렇게 47 시간 이상 공부한 모든 학생은 통과, 47 시간 미만 공부한 모든 학생은 탈락… 이렇게 예측할 수 있는 건데요. 그럼 이렇게 47 시간에 선을 긋고
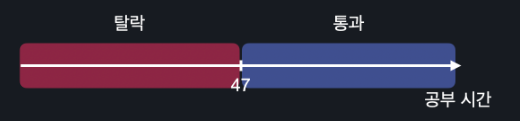
모든 데이터에 대해서 파란색 영역에 있으면, 통과, 빨간색 영역에 있으면 탈락이라고 할 수 있겠죠? 이렇게 분류를 할 때, 분류를 구별하는 경계선을 Decision Boundary라고 부릅니다.
속성이 2개일 때
ex) 공부시간, 모의고사 시험 점수로 시험을 통과했을지 예측 / 공부시간 = x1, 모의고사 시험 점수 = x2
가설함수는
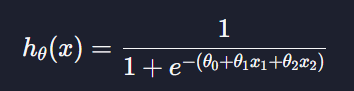
이렇게 나온다
그리고 이 함수의 결과가 0.5 이상이면 시험을 통과, 미만이면 탈락을 예측할 수 있는 건데요. 변수가 하나일 때 47 시간에 선을 그릴 수 있던 것처럼, 방금 말한 내용을 시각화하면 이런 선을 그릴 수 있습니다.
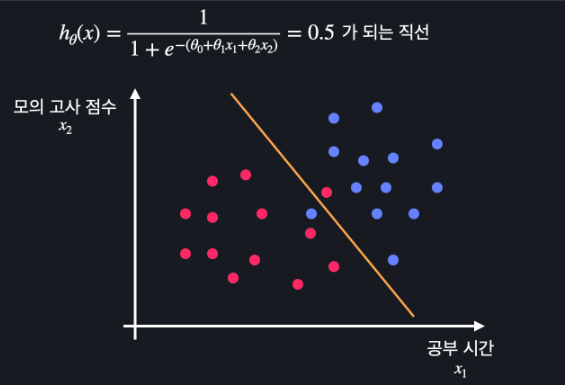
가설함수가 0.5가 되는 식을 풀면 변수 x1, x2의 관계식을 구할 수 있음
그 선이 함수가 데이터를 분류하는 기준선이 되고 통과와 탈락을 예측한다
이 때 Decision Boundary를 시각화 하면
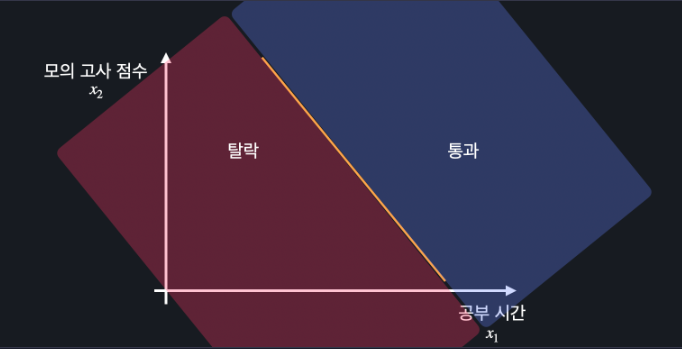
이렇게 된다
7.6 로그 손실
로지스틱 회귀 손실함수는 로그손실을 사용함
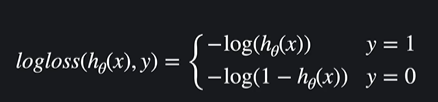
로그 손실은 이렇게 생겼다. 로그 손실함수는 예측값이 실제 결과와 얼마나 괴리가 있는지 알려줌
i) 실제 값이 1일 때
-
hθ(x) = 1이면 :
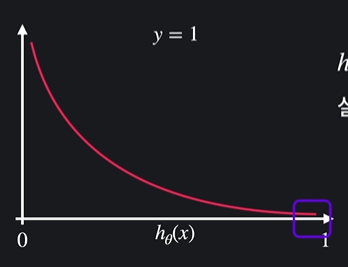
실제로 y=1이기 때문에 손실 0 -
hθ(x) = 0.8이면 (= 80%로 y=1이라고 예측):
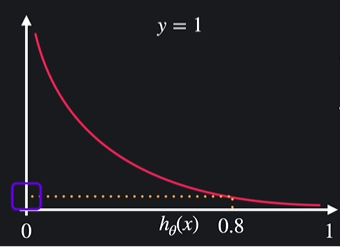
y=1이기 때문에 손실이 작음
ㄴ 이 그래프는 hθ(x)가 1에서 멀어질수록 잘못하고 있는거니까 손실을 엄청나게 키운다
ii) 실제 값이 0일 때
-
hθ(x) = 0이면 :
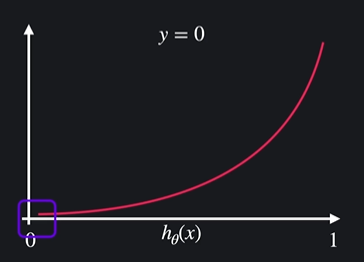
실제로 y-0이기 때문에 손실 0 -
hθ(x) = 0.2이면 (= 20%로 y=1이라고 예측) :
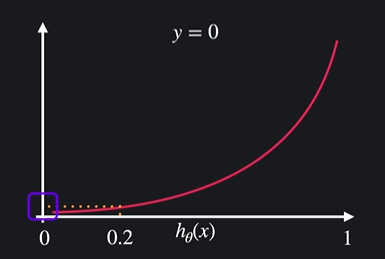
실제로 y=0이기 때문에 손실이 적음
ㄴ 이 그래프는 hθ(x)가 0에서 멀어질수록 잘못하고 있는거니까 손실을 엄청나게 키운다
- 로그 손실이라고 부르는 이유 : 손실의 정도를 로그함수로 결정하기 때문
7.7 로지스틱 회귀 손실 함수
우리가 선형회귀를 할 때에는 평균제곱오차를 사용해서 손실함수를 만들었음
로지스틱 회귀를 할 때에는 로그손실을 이용해서 손실함수를 만든다
로그 손실을 이용해서 로지스틱 회귀 손실함수를 만들면
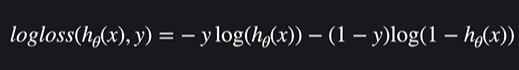
이 형태를 씀
y = 1일 때
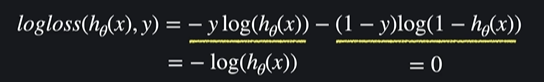
즉 -log(h(x))인 것임
y = 0일 때
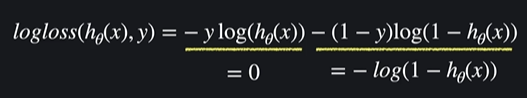
즉 -log(1-h(x))가 되는 것 !
우리가 하려는 것은 각 데이터의 손실을 구한 후 그 손실의 평균을 내는 것이당
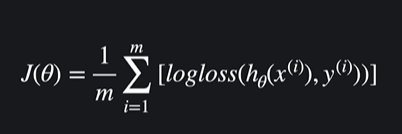
: 모든 데이터의 로그 손실을 계산한 후, 평균을 냄 -> 그걸로 가설함수를 평가
손실함수의 인풋은 θ인데 왜냐면 가설함수는 θ값들을 어떻게 설정하느냐에 따라 학습데이터의 손실이 달라지기 때문
만약 이 식에 로그 손실함수를 완전히 대입하고 싶으면
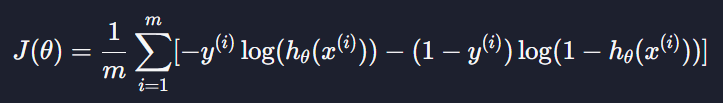
이렇게 하면 된다
7.8 로지스틱 회귀 경사 하강법
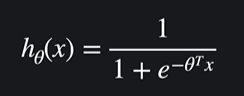
: 처음에 θ값들을 다 0 또는 임의로 설정
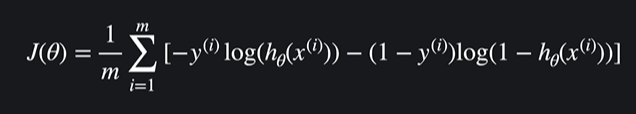
θ을 업데이트 해서 손실을 점점 최소화 시켜야 됨
ex)
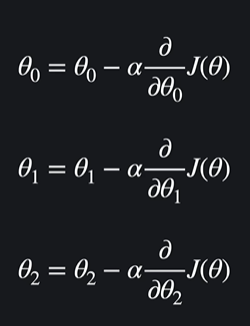
손실함수를 θ에 대해 편미분 하고 그 결과에 학습율 알파를 곱함 그 후에 기존의 θ에다가 값을 뺀다
-> 이렇게 모든 θ값들을 업데이트 하면 이게 경사하강을 1번 했다고 할 수 있음 --(반복)--> 손실 최소화
- 선형회귀든 로지스틱 회귀든 경사 하강할 때는 항상 이렇게 하는데 다른 점은 손실함수 J가 다르다는 점이다 !!
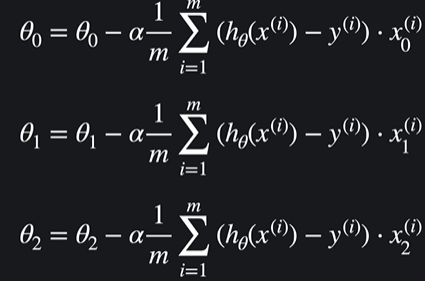
선형회귀랑 똑같음 !
일반화 하면
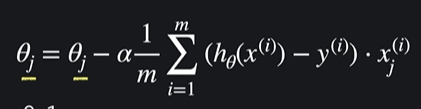
이런 식이 나온다. 선형회귀랑 같은데 유일하게 다른것은 h(x)인 가설함수임
선형회귀에서는 가설함수가 일차 함수였지만
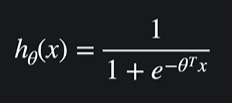
로지스틱 회귀에서는 가설함수가 시그모이드 함수 임
이 시그모이드 함수를 대입해서 각 세타 값을 업데이트 하면 된다 ~~
7.9 로지스틱 회귀 구현하기 쉽게 표현하기
입력 변수와 파라미터 표현
모든 입력 변수 데이터를 행렬에 넣으면
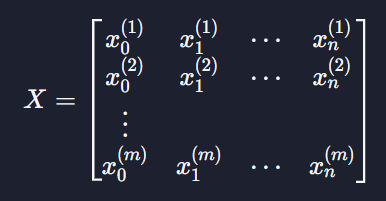
그리고 파라미터를 하나의 벡터로 하면
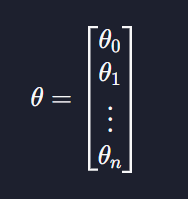
이렇게 표현이 가능하다
모든 데이터 예측 값
아까 입력변수와 파라미터를 이용해서
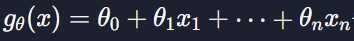
를 계산할 수 있다 이는 Xθ 와 같음 -> 이는 선형회귀 부분이랑 똑같다 !!
하지만 로지스틱 회귀는 선형회귀랑 가설함수 h(x)가 다르다
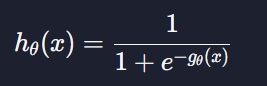
위에서 계산한 모든 결과 값을 시그모이드 함수에 넣어줘야 하는데
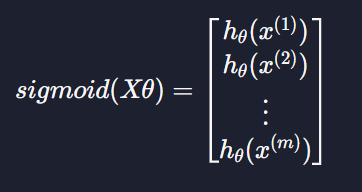
이렇게 Xθ의 모든 원소를 시그모이드 함수에 넣어준다 ~~
예측 오차
데이터의 목표변수 값은 하나이기 때문에
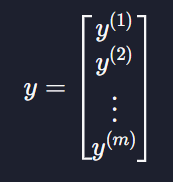
이렇게 표현해준다
sigmoid(Xθ)에서 y를 빼면
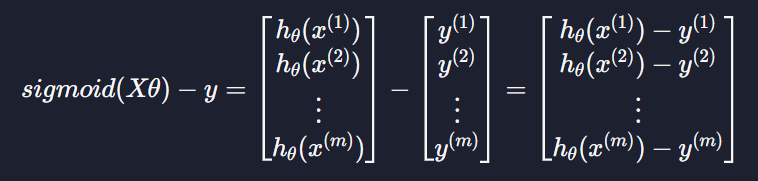
이렇게 나오고 우리는 이걸 error라고 부른다
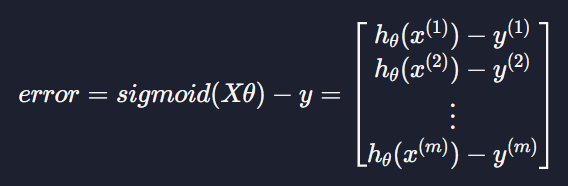
경사 하강법
로지스틱회귀는 선형회귀 경사 하강법 공식이랑 똑같다 !!
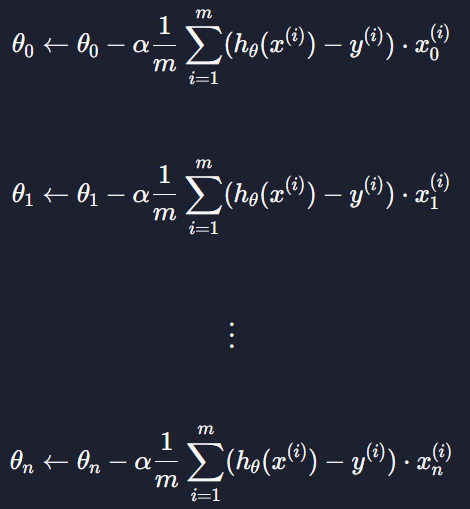
이렇게 0부터 n까지의 θ값들을 업데이트 하는데, 그렇기 때문에 경사 하강법도 다중선형 회귀를 할 때랑 같이 표현한다
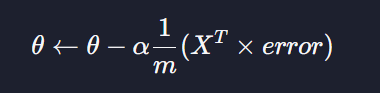
이렇게 쉽게 표현할 수 있당 ~~
7.10 (실습) 로지스틱 회귀 가정 함수 구현하기
이번 과제에서는 로지스틱 회귀 가정 함수를 구현해 보겠습니다.
입력 변수와 파라미터를 아래 식처럼 표현합니다.

행렬의 모든 원소를 시그모이드 함수에 넣어 계산해 준다는 표현을 sigmoid() 라고 할 때 로지스틱 회귀 가설 함수는 아래와 같이 표현할 수 있습니다.
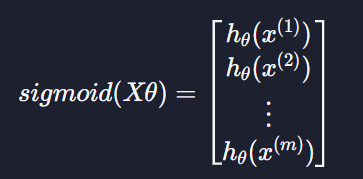
행렬의 모든 원소에 대해서 시그모이드 함수 결과 값을 계산해주는 sigmoid함수는 이미 구현해 놨는데요. sigmoid 함수를 사용해서 로지스틱 함수의 가정 함수를 구현해 보세요.
sigmoid 함수
이렇게 시그모이드 함수 안에 numpy 배열을 넣으면 모든 원소를 시그모이드 함수에 넣은 결과 값을 구할 수 있습니다.
np_array_1 = np.array([-3, -2, -1, 0, 1, 2, 3])
sigmoid(np_array_1) # array([ 0.04742587, 0.11920292, 0.26894142, 0.5, 0.73105858, 0.88079708, 0.95257413])prediction함수
prediction 함수는 설계 행렬 X를 X로, 파라미터 θ를 theta로 받습니다. 그리고 모든 데이터에 대해서 로지스틱 회귀 예측 값을 numpy 배열로 리턴합니다.
code
import numpy as np
def sigmoid(x):
"""시그모이드 함수"""
return 1 / (1 + np.exp(-x))
def prediction(X, theta):
"""로지스틱 회귀 가정 함수"""
return sigmoid(X@theta)
# 입력 변수
hours_studied = np.array([0.2, 0.3, 0.7, 1, 1.3, 1.8, 2, 2.1, 2.2, 3, 4, 4.2, 4, 4.7, 5.0, 5.9]) # 공부 시간 (단위: 100시간)
gpa_rank = np.array([0.9, 0.95, 0.8, 0.82, 0.7, 0.6, 0.55, 0.67, 0.4, 0.3, 0.2, 0.2, 0.15, 0.18, 0.15, 0.05]) # 학년 내신 (백분률)
number_of_tries = np.array([1, 2, 2, 2, 4, 2, 2, 2, 3, 3, 3, 3, 2, 4, 1, 2]) # 시험 응시 횟수
# 설계 행렬 X 정의
X = np.array([
np.ones(16),
hours_studied,
gpa_rank,
number_of_tries
]).T
# 파라미터 theta 정의
theta = [0.5, 0.3, -2, 0.2]
prediction(X, theta)7.11 (실습) 로지스틱 회귀 경사 하강법 구현하기
로지스틱 회귀 경사 하강법은
입력 변수, 파라미터, 예측값 오차를 이렇게 표현할 때:

다중 선형 회귀를 구현할 때와 똑같이

이렇게 표현할 수 있다고 했는데요. 이번 과제에서는 이걸 이용해서 경사 하강법을 직접 구현해 보겠습니다.
gradient_descent함수
gradient_descent 함수는 파라미터로 입력 변수 X, 파라미터 theta, 목표 변수 y, 경사 하강 횟수 iterations 그리고 학습률 alpha를 받습니다. 이 입력 변수들로 경사 하강법을 사용해서 찾은 최적화된 theta를 리턴해 줍니다.
code
import numpy as np
def sigmoid(x):
"""시그모이드 함수"""
return 1 / (1 + np.exp(-x))
def prediction(X, theta):
"""로지스틱 회귀 가정 함수"""
return sigmoid(X@theta)
def gradient_descent(X, theta, y, iterations, alpha):
"""로지스틱 회귀 경사 하강 알고리즘"""
m = len(X) # 입력 변수 개수 저장
for _ in range(iterations):
theta = theta - alpha * 1 / m * (X.T @ (sigmoid(X@theta) - y))
return theta
# 입력 변수
hours_studied = np.array([0.2, 0.3, 0.7, 1, 1.3, 1.8, 2, 2.1, 2.2, 3, 4, 4.2, 4, 4.7, 5.0, 5.9]) # 공부 시간 (단위: 100시간)
gpa_rank = np.array([0.9, 0.95, 0.8, 0.82, 0.7, 0.6, 0.55, 0.67, 0.4, 0.3, 0.2, 0.2, 0.15, 0.18, 0.15, 0.05]) # 학년 내신 (백분률)
number_of_tries = np.array([1, 2, 2, 2, 4, 2, 2, 2, 3, 3, 3, 3, 2, 4, 1, 2]) # 시험 응시 횟수
# 목표 변수
passed = np.array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1]) # 시험 통과 여부 (0: 탈락, 1:통과)
# 설계 행렬 X 정의
X = np.array([
np.ones(16),
hours_studied,
gpa_rank,
number_of_tries
]).T
# 입력 변수 y 정의
y = passed
theta = [0, 0, 0, 0] # 파라미터 초기값 설정
theta = gradient_descent(X, theta, y, 300, 0.1) # 경사 하강법을 사용해서 최적의 파라미터를 찾는다
theta이렇게 적을 수도 있다 ~
def gradient_descent(X, theta, y, iterations, alpha):
"""로지스틱 회귀 경사 하강 알고리즘"""
m = len(X) # 입력 변수 개수 저장
for _ in range(iterations):
error = prediction(X, theta) - y
theta = theta - alpha / m * (X.T @ error)
return theta7.12 분류가 3개 이상일 때
ex) 이메일을 세가지로 분류할 때

그리고 이걸 그래프에 나타낸다
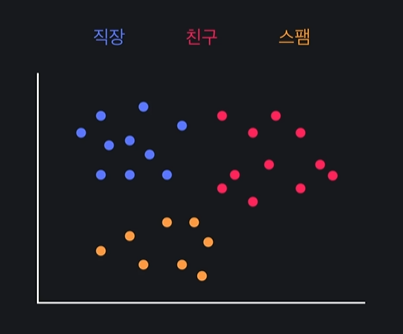
분류해보기 !
1) 직장인지 아닌지 분류하기 -(학습)-> h0(x)로 분류 (= 직장 메일일 확률을 리턴하는 함수)
2) 친구인지 아닌지 분류하기 -(학습)-> h1(x)로 분류 (= 친구 메일일 확률을 리턴하는 함수)
3) 스팸인지 아닌지 분류하기 -(학습)-> h2(x)로 분류 (= 스팸 메일일 확률을 리턴하는 함수)
이제 이메일 데이터들을 세개의 가설함수에 각각 넣는다 !

이런 결과가 나왔다면 직장 메일이 나올 확률이 60%, 친구 메일이 나올 확률이 45%, 스팸 메일이 나올 확률이 78% 이다
=> 스팸 메일이 나올 확률이 가장 높기 때문에 이 메일을 스팸메일로 분류한다
7.13 로지스틱 회귀와 정규 방정식
로지스틱 회귀에서는 선형회귀와 같이 정규 방정식과 같은 단순 행렬 연산만으로는 손실 함수의 최소 지점을 찾을수가 없다
로지스틱 회귀 알고리즘에서 θj에 대한 편미분 함수를 구하면
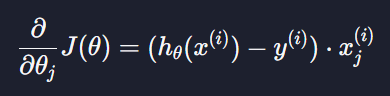
이렇게 나왔고 여기서 가설함수는
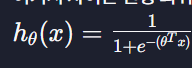
이거였당
로지스틱 회귀에서 손실함수 J(로그 손실)가 아래로 볼락한 convex이다. 그래서 경사 하강법을 사용하면 항상 최적의 θ갑슬을 찾을 수 있다. 하지만 J에 대한 편미분 원소들이 선형식이 아니여서 일차식으로 표현이 불가능 !!
= 단순 행렬 연산만으로는 최소 지점을 찾아낼 수 없다
7.14 scikit-learn 로지스틱 회귀 데이터 준비
저번과는 다른 붓꽃에 대한 데이터셋을 불러오는 모듈을 임포트 했다
from sklearn.datasets import load_iris # 붓꽃에 대한 데이터셋
import pandas as pd데이터셋을 변수에 넣어준다 ~
iris_data = load_iris()한번 설명을 프린트 해봄
print(iris_data.DESCR)output
.. _iris_dataset:
Iris plants dataset
--------------------
**Data Set Characteristics:**
:Number of Instances: 150 (50 in each of three classes)
:Number of Attributes: 4 numeric, predictive attributes and the class
:Attribute Information:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
- class:
- Iris-Setosa
- Iris-Versicolour
- Iris-Virginica
:Summary Statistics:
============== ==== ==== ======= ===== ====================
Min Max Mean SD Class Correlation
============== ==== ==== ======= ===== ====================
sepal length: 4.3 7.9 5.84 0.83 0.7826
sepal width: 2.0 4.4 3.05 0.43 -0.4194
petal length: 1.0 6.9 3.76 1.76 0.9490 (high!)
petal width: 0.1 2.5 1.20 0.76 0.9565 (high!)
============== ==== ==== ======= ===== ====================
:Missing Attribute Values: None
:Class Distribution: 33.3% for each of 3 classes.
:Creator: R.A. Fisher
:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
:Date: July, 1988
The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.
This is perhaps the best known database to be found in the
pattern recognition literature. Fisher's paper is a classic in the field and
is referenced frequently to this day. (See Duda & Hart, for example.) The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant. One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other.
.. topic:: References
- Fisher, R.A. "The use of multiple measurements in taxonomic problems"
Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions to
Mathematical Statistics" (John Wiley, NY, 1950).
- Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.
(Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.
- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New System
Structure and Classification Rule for Recognition in Partially Exposed
Environments". IEEE Transactions on Pattern Analysis and Machine
Intelligence, Vol. PAMI-2, No. 1, 67-71.
- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule". IEEE Transactions
on Information Theory, May 1972, 431-433.
- See also: 1988 MLC Proceedings, 54-64. Cheeseman et al"s AUTOCLASS II
conceptual clustering system finds 3 classes in the data.
- Many, many more ...입력 변수들을 데이터프레임으로 만들어줌
X = pd.DataFrame(iris_data.data, columns = iris_data.feature_names)
Xoutput
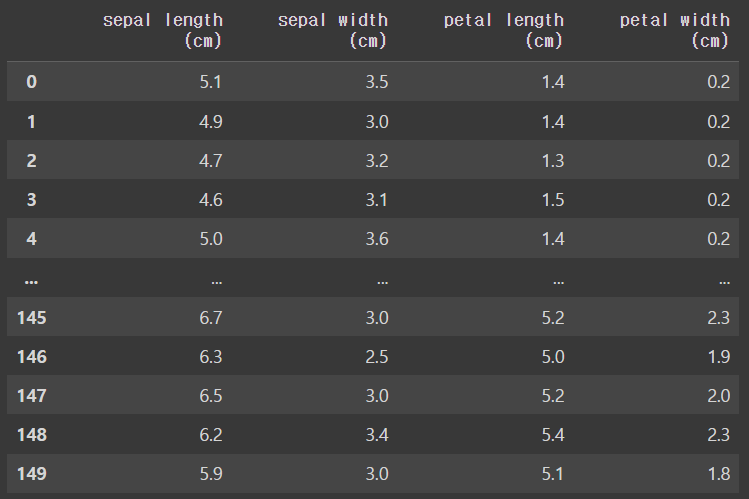
목표 변수 또한 만들어준당
y = pd.DataFrame(iris_data.target, columns = ['class'])
youtput
데이터 준비 끝 !!
7.15 scikit-learn으로 로지스틱 회귀 쉽게 하기
변수 설정
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 5)로지스틱 회귀에서는 이 코드를 쓰는 것이 좋다고 함 (에러가 날 수도 잇어서)
이는 y_train이라는 면수가 dataframe 혹은 series일 때 y_train.values는 이를 numpy 배열로 변환 시켜주고 ravel()함수는 다차원 배열을 1차원 배열로 평평하게 만들어주는 역할을 함
y_train = y_train.values.ravel()solver = 모델을 최적화 할때 어떤 알고리짐을 쓸지 선택
max_iter = 최적화를 할 때 그 과정을 몇번 반복할지 결정해줌
model = LogisticRegression(solver = 'saga', max_iter = 2000)trainig set을 학습시켜 준다
model.fit(X_train, y_train)output
test set을 예측해줌
model.predict(X_test) # 분류 문제여서 아웃풋이 0,1,2 밖에 없음output
array([1, 2, 2, 0, 2, 1, 0, 2, 0, 1, 1, 2, 2, 2, 0, 0, 2, 2, 0, 0, 1, 2,
0, 1, 1, 2, 1, 1, 1, 2])모델의 분류 확률을 계산해준다
model.score(X_test, y_test) # 이 모델이 0.9666666666666667의 확률로 제대로 분류한다는 뜻output
0.96666666666666677.16 (실습) 로지스틱 회귀로 와인 종류 분류하기
이번 과제에서는 scikit-learn을 이용해서 다양한 와인 데이터를 분류해 볼게요. 데이터는 scikit-learn에서 기본적으로 사용할 수 있는 와인 데이터를 사용할 거고요. 이걸 가지고 와서 입력과 목표 변수로 나누는 부분까지는 코드가 작성돼 있습니다. 여러분이 직접 아래 내용들을 코드로 작성해 주세요.
- 데이터를 training/test set으로 나눈다.
- scikit-learn의 LogisticRegression 모델을 학습시킨다.
- 학습시킨 모델을 이용해서 test set 데이터에 대해 예측한다.
(본격적으로 시작하기 전에print(wine_data.DESCR)을 실행해서 데이터 셋을 살펴보는 걸 잊지마세요!)
조건
train_test_split함수의 옵셔널 파라미터는test_size=0.2, random_state=5이렇게 설정해 주세요.- 경고 메시지가 나오지 않도록, 학습시키기 전에
y_train = y_train.values.ravel()이 코드를 추가하는 걸 잊지마세요. - LogisticRegression 모델의 옵셔널 파라미터는
solver='saga', max_iter=7500이렇게 설정해 주세요. - test set 데이터 예측 값들을 저장하는 numpy 배열 변수 이름은
y_test_predict으로 정의하세요.
code
# 필요한 라이브러리 import
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import pandas as pd
wine_data = datasets.load_wine()
# 입력 변수를 사용하기 편하게 pandas dataframe으로 변환
X = pd.DataFrame(wine_data.data, columns=wine_data.feature_names)
# 목표 변수를 사용하기 편하게 pandas dataframe으로 변환
y = pd.DataFrame(wine_data.target, columns=['Y/N'])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=5)
y_train = y_train.values.ravel()
# sci-kit learn에서 로지스틱 모델을 가지고 온다
logistic_model = LogisticRegression(solver = 'saga', max_iter = 7500)
# 학습 데이터를 이용해서 모델을 학습 시킨다
logistic_model.fit(X_train, y_train)
# 로지스틱 회귀 모델를 이용해서 각 와인 데이터 분류를 예측함
y_test_predict = logistic_model.predict(X_test)
# 로지스틱 회귀 모델의 성능 확인 (정확성 %를 리턴함)
score = logistic_model.score(X_test, y_test)
y_test_predict, score