
- 모델이 너무 간단해서 복잡한 곡선 관계를 학습할 수 없다 =
편향이 높다 - 모델이 데이터들 사이의 관계를 완벽하게 학습했다 =
편향이 낮다
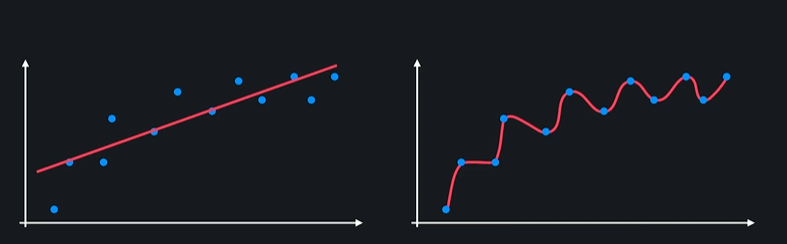
그럼 편향이 낮은 모델이 항상 편향이 높은 모델보다 좋을까??
ㄴ 꼭 그렇지는 않다
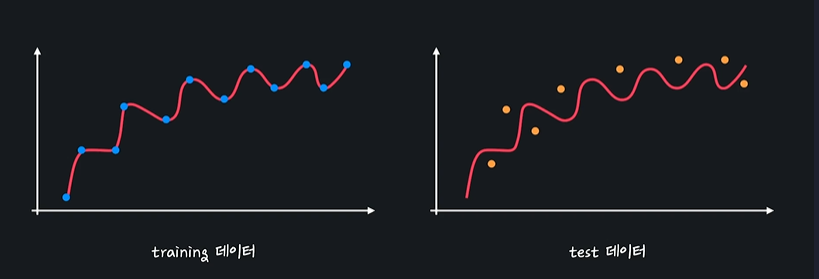
이 모델은 training 관계를 완벽하게 이해한 모델이다. 하지만 처음 보는 테스트 데이터들에 대해서는 이해를 못해서 성능이 별로 안좋다 -> 분산이 높다
분산 = 데이터 셋 별로 모델이 얼마나 일관된 성능을 보여주는지
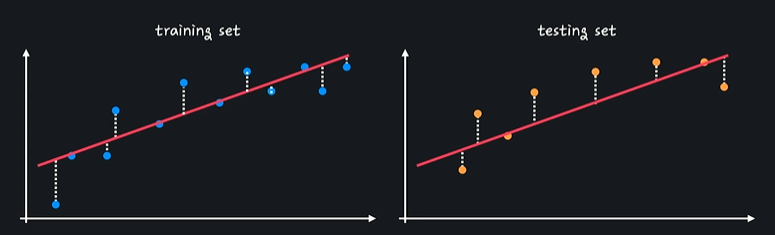
training set과 test set에서 성능에 큰 차이가 없다 -> 분산이 낮다
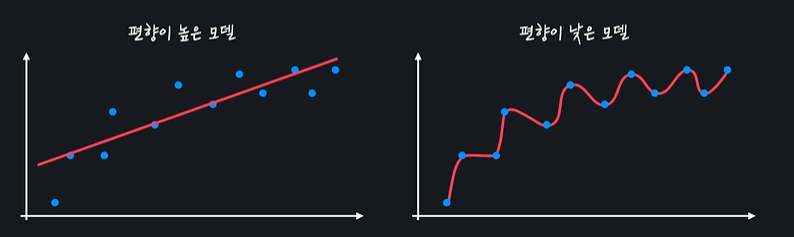
- 편향이 높은 모델은 너무 간단해서 주어진 데이터의 관계를 잘 학습하기 못한다
- 편향이 낮은 모델은 주어진 데이터의 관계를 잘 학습한다
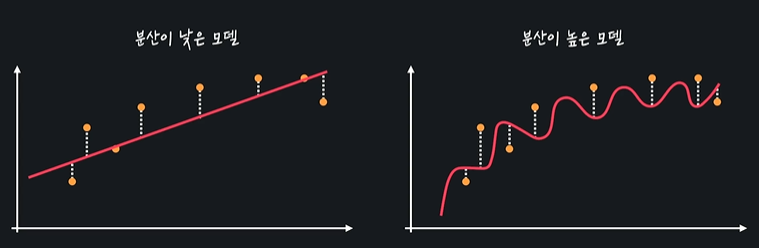
- 분산은 다양한 테스트 데이터가 주어졌을 때 모델의 성능이 얼마나 일관적인지를 나타낸다
2.2 편향-분산 트레이드오프
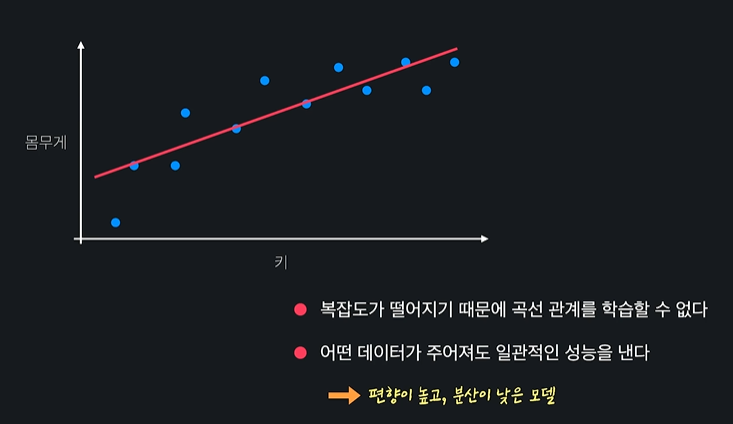
ㄴ 이런 경우 과소적합(underfit) 된 것이다
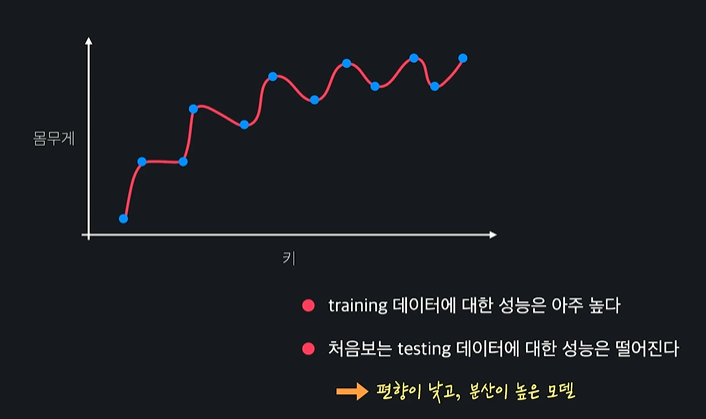
ㄴ 이런 경우 과적합(overfit) 된 것이다
모델이 training data 관계를 잘 나타내지 못하면 과소적합, 관계를 지나치게 잘 나탄면 과적합이다
일반적으로 편향과 분산은 하나가 줄어들수록 하나는 늘어나는 관계가 있다 = 편향-분산 트레이드오프
ㄴ 편향과 분산, 다르게는 과소적합과 과적합의 적당한 밸런스를 찾아야한다
2.3 scikit-learn으로 과적합 문제 직접 보기
필요한 모듈 임포트 하기
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures
from math import sqrt
import numpy as np
import pandas as pd파일 경로 변수 저장 & 필요없는 데이터 삭제
ADMISSION_FILE_PATH = 'drive/MyDrive/dataScience/data/admission_data.csv'
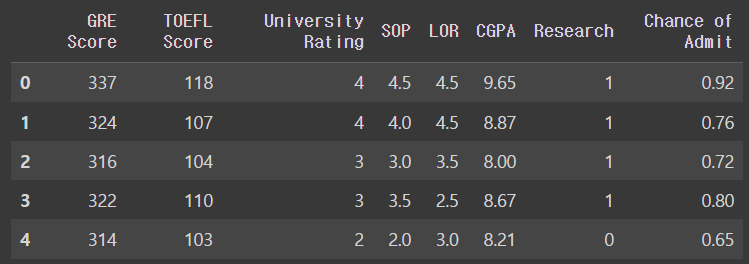
admission_df = pd.read_csv(ADMISSION_FILE_PATH).drop('Serial No.', axis = 1)데이터 프레임 확인하기
admission_df.head()output
다항식 특성을 데이터에 추가해서 새로운 데이터 프레임 X를 생성
X = admission_df.drop(['Chance of Admit '],axis = 1) # 입력변수 따로 저장
polynomial_transformer = PolynomialFeatures(6) #6차항 변형기 정의
polynomial_features = polynomial_transformer.fit_transform(X.values) # 인풋 데이터 넣어서 변수를 높은 차항으로 해줌
features = polynomial_transformer.get_feature_names_out(X.columns) #변수 이름 생성
X = pd.DataFrame(polynomial_features, columns = features)
X.head()output
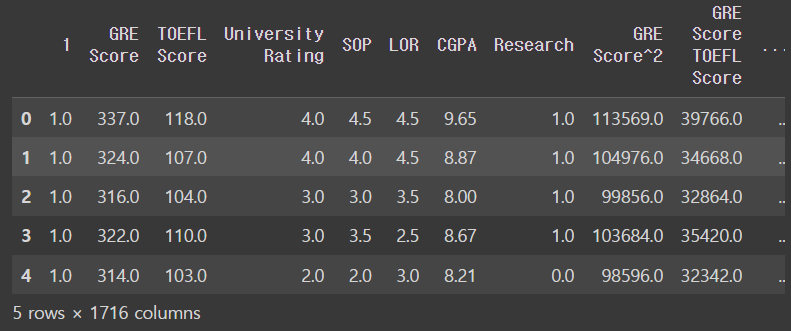
목표 변수
y = admission_df[['Chance of Admit ']]
y.head()output
training set, test set 변수 저장
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3, random_state = 5)선형 회귀 모델로 데이터 학습시키기
model = LinearRegression()
model.fit(X_train, y_train)output
trainig set과 test set으로 예측값 계산하기
y_train_predict = model.predict(X_train) # training set으로 예측값 계산
y_test_predict = model.predict(X_test) # test set으로 예측값 계산그리고 나서 각각 성능을 평균 제곱근 오차로 평가하기
mse = mean_squared_error(y_train, y_train_predict)
print('training set에서의 성능')
print('-----------------------')
print(sqrt(mse))
print()
mse = mean_squared_error(y_test, y_test_predict)
print('test set에서의 성능')
print('-----------------------')
print(sqrt(mse))output
training set에서의 성능
-----------------------
0.0015048220797102617
test set에서의 성능
-----------------------
5.09066922665522452.4 정규화 개념
ex) 모델이 과적합돼서 굉장히 복잡한 다항함수가 나왔을 때
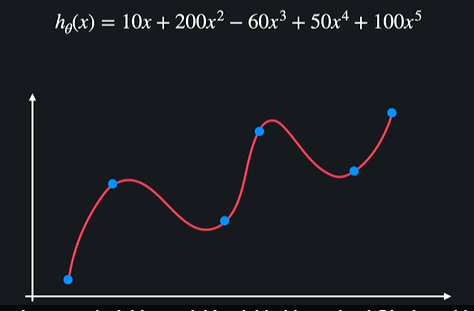
ㄴ 과적합된 함수는 보통 위아래로 많이 왔다갔다 한다
함수가 이렇게 급격히 변한다는 건 세타값들(계수)가 되게 크다는 것
정규화 = 이 세타값들이 너무 커지는 것을 방지하는 방법이다 ! -> 가설함수를 완만하게 만들어줌 = 여러 데이터셋에서 일관된 성능을 보이기 때문에 과적합을 예방함
2.5 L1, L2 정규화
정규화 = 손실함수 + 정규화 항
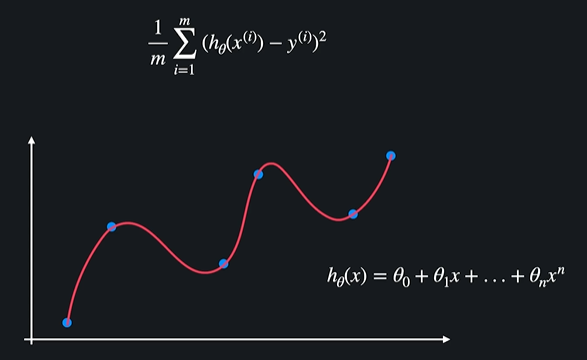
데이터와 가장 잘 맞는 선을 찾는게 목표 = training data에 대한 평균 제곱 오차를 최소화 한다는 뜻
과적합 함수 = 오차는 굉장히 작지만 세타값들이 너무 커서 성능이 별루 !!
새로운 좋은 가설함수의 기준
: training data에 대한 오차도 작고 세타값들도 작아야지 좋은 가설함수
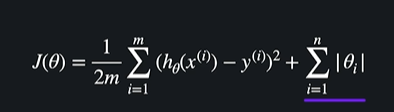
여기서 세타값들이 크면 가설함수가 안 좋고 세타값들이 작으면 가설함수가 좋다는 뜻이당
ex)

h(x)는 g(x)보다 평균 제곱 오차는 작지만 세타값들이 커서 덜 좋은 가설함수가 된다
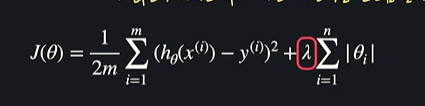
사실 정규화 항에는 lamda라는 상수를 곱해준다
ㄴ 이것은 세타값들이 커지는 것에 대한 패널티를 얼만큼 줄지 정할 수 있음
ex) lamda = 100 : 세타값들이 조금만 커져도 손실함수가 굉장히 커져서 세타값을 줄이는게 우선이 됨
lamda = 0.01 : 세타값들이 많이 커져도 손실함수가 별로 안커져서 평균 제곱 오차를 줄이는게 우선이 됨
L1 정규화
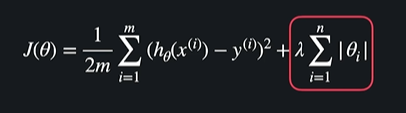
L1정규화를 적용한 회귀 모델을 Lasso Regression, Lasso 모델이라고 한다
L2 정규화
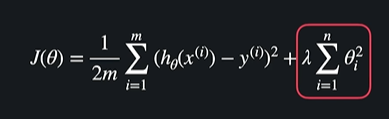
L1과는 살짝 다르게 세타값의 제곱을 더해주는 것
L2 정규화를 적용한 회귀 모델을 Ridge Regression, Ridge 모델이라고 한다
- 정리
정규화 = 머신러닝 모델을 학습시킬 때 세타값들이 너무 커지는 것을 방지해주는 기법
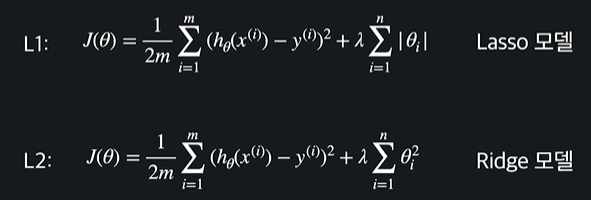
데이터에 대한 오차와 θ값 중 어떤 것을 줄이는 게 더 중요한지는 상수 λ에 따라 결정됩니다. λ가 클수록 θ값을 줄이는 게 중요하고, λ가 작을수록 데이터에 대한 오차를 줄이는 게 중요한 거죠.
2.6 scikit-learn으로 과적합 문제 해결해보기
총 코드
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import MinMaxScaler
from math import sqrt
import numpy as np
import pandas as pd
ADMISSION_FILE_PATH = 'drive/MyDrive/dataScience/data/admission_data.csv'
admission_df = pd.read_csv(ADMISSION_FILE_PATH).drop('Serial No.', axis = 1)
X = admission_df.drop(['Chance of Admit '],axis = 1) # 입력변수 따로 저장
polynomial_transformer = PolynomialFeatures(6) #6차항 변형기 정의
polynomial_features = polynomial_transformer.fit_transform(X.values) # 인풋 데이터 넣어서 변수를 높은 차항으로 해줌
features = polynomial_transformer.get_feature_names_out(X.columns) #변수 이름 생성
X = pd.DataFrame(polynomial_features, columns = features)
y = admission_df[['Chance of Admit ']]
# X_train을 스케일링 (MinMax 스케일링) - 데이터를 [0, 1] 범위로 조정
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
# Lasso 모델 생성 및 학습
model = Lasso(alpha=0.001, max_iter=1000) #L2 쓰고 싶으면 Lasso -> Ridge로 바꾸면 됨
model.fit(X_train_scaled, y_train)
y_train_predict = model.predict(X_train) # training set으로 예측값 계산
y_test_predict = model.predict(X_test) # test set으로 예측값 계산
# 각각 성능 평균 제곱근 오차로 평가
mse = mean_squared_error(y_train, y_train_predict)
print('training set에서의 성능')
print('-----------------------')
print(sqrt(mse))
print()
mse = mean_squared_error(y_test, y_test_predict)
print('test set에서의 성능')
print('-----------------------')
print(sqrt(mse))바뀐게 뭐가 있느냐 !! 보면
우선 LinearRegression을 import 했었지만 이제는
from sklearn.linear_model import Lasso를 import한다
그리고 데이터 학습 시키는 부분에서도 Lasso()를 써줌
# X_train을 스케일링 (MinMax 스케일링) - 데이터를 [0, 1] 범위로 조정
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
# Lasso 모델 생성 및 학습
model = Lasso(alpha=0.001, max_iter=1000) #L2 쓰고 싶으면 Lasso -> Ridge로 바꾸면 됨
model.fit(X_train_scaled, y_train)ㄴ 근데 이게 강의랑 버전이 달라서 나는 이상하게 쓰게 됐다
원래 강의에서는
model = Lasso(alpha = 0.001, max_iter = 1000, normalize = True)
model.fit(X_train, y_train)이거였음
그 다음에 평가했는데
# 각각 성능 평균 제곱근 오차로 평가
mse = mean_squared_error(y_train, y_train_predict)
print('training set에서의 성능')
print('-----------------------')
print(sqrt(mse))
print()
mse = mean_squared_error(y_test, y_test_predict)
print('test set에서의 성능')
print('-----------------------')
print(sqrt(mse))output
training set에서의 성능
-----------------------
908.6131622983793
test set에서의 성능
-----------------------
902.4631945099151ㄴ 이렇게 개같이 나와서 아무래도 위에 학습시키는 부분에서 이상해진듯 하다.. 우울
2.7 (실습) L1 정규화 직접 해보기
저희가 이번 과제에서 사용하는 데이터는 환자들의 보험료 데이터입니다. 보험료 데이터에는 고객의 나이, 성별, bmi, 자녀가 몇 명인지, 흡연 여부, 출신 지역 그리고 보험료가 있습니다.
# 데이터 파일 경로 정의
INSURANCE_FILE_PATH = '../datasets/insurance.csv'
insurance_df = pd.read_csv(INSURANCE_FILE_PATH) # 데이터를 pandas dataframe으로 갖고 온다 (insurance_df.head()를 사용해서 데이터를 한번 살펴보세요!)아래 데이터 준비 코드를 살펴보시고, 각 단계에서 출력문을 사용해서 데이터가 어떻게 바뀌고 있는지 꼭 확인을 해보시면서 넘어가시길 바랍니다.
insurance_df = pd.get_dummies(data=insurance_df, columns=['sex', 'smoker', 'region']) # 필요한 열들에 One-hot Encoding을 해준다
# 입력 변수 데이터를 따로 새로운 dataframe에 저장
X = insurance_df.drop(['charges'], axis=1)
polynomial_transformer = PolynomialFeatures(4) # 4 차항 변형기를 정의
polynomial_features = polynomial_transformer.fit_transform(X.values) # 4차 항 변수로 변환
features = polynomial_transformer.get_feature_names(X.columns) # 새로운 변수 이름들 생성
X = pd.DataFrame(polynomial_features, columns=features) # 다항 입력 변수를 dataframe으로 만들어 준다
y = insurance_df[['charges']] # 목표 변수 정의데이터 준비 부분 코드가 좀 많기는 합니다. 요약해서 말씀드릴게요.
- 보험료 데이터를 가지고 온다.
- 입력 변수를 따로 저장한다.
- 입력 변수를 4차 항으로 변환한다.
- 변환한 입력 변수와 목표 변수를 따로 새로운 dataframe에 저장한다.
이번 과제에서는 Lasso 모델과, 입력 변수 X, 그리고 목표 변수 y를 사용해서 보험료를 예측해 보겠습니다. 밑에 나와 있는 내용들을 코드로 직접 구현해 보세요!
- train_test_split을 이용해서 데이터를 training 그리고 test set으로 나누세요. (옵셔널 파라미터는 test_size=0.3, random_state=5로 해 주세요)
- Lasso 모델을 만들고, training set 데이터를 이용해서 학습시키세요. (Lasso 모델의 옵셔널 파라미터는 alpha=1, max_iter=2000, normalize=True로 해 주세요.)
- 각각 training과 test 데이터에 대한 예측값을 y_train_predict, y_test_predict 변수에 저장해 주세요.
code
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures
from math import sqrt
import numpy as np
import pandas as pd
# 데이터 파일 경로 정의
INSURANCE_FILE_PATH = './datasets/insurance.csv'
insurance_df = pd.read_csv(INSURANCE_FILE_PATH) # 데이터를 pandas dataframe으로 갖고 온다 (insurance_df.head()를 사용해서 데이터를 한 번 살펴보세요!)
insurance_df = pd.get_dummies(data=insurance_df, columns=['sex', 'smoker', 'region']) # 필요한 열들에 One-hot Encoding을 해준다
# 입력 변수 데이터를 따로 새로운 dataframe에 저장
X = insurance_df.drop(['charges'], axis=1)
polynomial_transformer = PolynomialFeatures(4) # 4 차항 변형기를 정의
polynomial_features = polynomial_transformer.fit_transform(X.values) # 4차 항 변수로 변환
features = polynomial_transformer.get_feature_names(X.columns) # 새로운 변수 이름들 생성
X = pd.DataFrame(polynomial_features, columns=features) # 다항 입력 변수를 dataframe으로 만들어 준다
y = insurance_df[['charges']] # 목표 변수 정의
# 데이터를 training과 test 셋으로 나누기
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3, random_state = 5)
# 회귀 모델에 L1 정규화를 적용한 모델인 Lasso 모델을 새롭게 정의
model = Lasso(alpha = 1, max_iter = 2000, normalize = True)
# fit() 메소드를 사용해서 training 셋 데이터를 이용해서 새롭게 정의
model.fit(X_train, y_train)
# predict() 메소드를 각각 training과 test 셋 입력 변수들에 대한 예측 값들을 찾아내기
# 각 예측 값들을 y_train_predict과 y_test_predict에 저장
y_train_predict = model.predict(X_train)
y_test_predict = model.predict(X_test)
mse = mean_squared_error(y_train, y_train_predict)
print("training set에서 성능")
print("-----------------------")
print(f'오차: {sqrt(mse)}')
mse = mean_squared_error(y_test, y_test_predict)
print("testing set에서 성능")
print("-----------------------")
print(f'오차: {sqrt(mse)}')2.8 (실습) L2 정규화 직접 해보기
이번 과제에서는 sklearn 라이브러리의 linear_model 모듈에서 Ridge 모델을 사용해서 L2 정규화를 직접 해 보겠습니다.
이번 과제에서 사용할 도구들을 import해 줍니다. L1 직접 해보기 과제와는 다르게 sklearn 라이브러리 linear_model 모듈에서 Lasso 가 아닌 Ridge를 import해 옵니다.
(이 부분은 L1 직접 해보기 과제와 동일합니다.)
저희가 이번 과제에서 사용하는 데이터는 환자들의 보험료 데이터입니다. 보험료 데이터에는 고객의 나이, 성별, bmi, 자녀가 몇 명인지, 흡연 여부, 출신 지역 그리고 보험료가 있습니다.
아래 데이터 준비 코드를 살펴보시고, 각 단계에서 출력문을 사용해서 데이터가 어떻게 바뀌고 있는지 꼭 확인을 해 보시면서 넘어가시길 바랍니다.
데이터 준비 부분 코드가 좀 많기는 합니다. 요약해서 말씀드릴게요.
- 보험료 데이터를 가지고 온다.
- 입력 변수를 따로 저장한다.
- 입력 변수를 4차 항으로 변환한다.
- 변환한 입력 변수와 목표 변수를 따로 새로운 dataframe에 저장한다.
이번 과제에서는 Ridge 모델과, 입력 변수 X, 그리고 목표 변수 y를 사용해서 보험료를 예측해 보겠습니다. 밑에 나와 있는 내용들을 코드로 구현해 보세요!
- train_test_split을 이용해서 데이터를 training 그리고 test set으로 나누세요. (옵셔널 파라미터는 test_size=0.3, random_state=5로 해 주세요)
- Ridge 모델을 만들고, training set 데이터를 이용해서 학습시키세요 (Ridge 모델의 옵셔널 파라미터는 alpha=0.01, max_iter=2000, normalize=True로 해 주세요)
- 각각 training과 test 데이터에 대한 예측값을 y_train_predict, y_test_predict 변수에 저장해 주세요.
code
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures
from math import sqrt
import numpy as np
import pandas as pd
INSURANCE_FILE_PATH = './datasets/insurance.csv'
insurance_df = pd.read_csv(INSURANCE_FILE_PATH)
insurance_df = pd.get_dummies(data=insurance_df, columns=['sex', 'smoker', 'region'])
# 기존 데이터에서 입력 변수 데이터를 따로 저장한다
X = insurance_df.drop(['charges'], axis=1)
polynomial_transformer = PolynomialFeatures(4) # 4 차항 변형기를 정의한다
polynomial_features = polynomial_transformer.fit_transform(X.values) # 데이터 6차 항 변수로 바꿔준다
features = polynomial_transformer.get_feature_names(X.columns) # 변수 이름들도 바꿔준다
# 새롭게 만든 다항 입력 변수를 dataframe으로 만들어 준다
X = pd.DataFrame(polynomial_features, columns=features)
y = insurance_df[['charges']]
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3, random_state = 5)
# 회귀 모델에 L2 정규화를 적용한 모델인 Ridge 모델을 새롭게 정의
model = Ridge(alpha = 0.01, max_iter = 2000, normalize = True)
# fit() 메소드를 사용해서 training 셋 데이터를 이용해서 새롭게 정의
model.fit(X_train, y_train)
# predict() 메소드를 각각 training과 test 셋 입력 변수들에 대한 예측 값들을 찾아내기
# 각 예측 값들을 y_train_predict과 y_test_predict에 저장
y_train_predict = model.predict(X_train)
y_test_predict = model.predict(X_test)
# 테스트 코드
mse = mean_squared_error(y_train, y_train_predict)
print("training set에서 성능")
print("-----------------------")
print(f'오차: {sqrt(mse)}')
mse = mean_squared_error(y_test, y_test_predict)
print("testing set에서 성능")
print("-----------------------")
print(f'오차: {sqrt(mse)}')2.9 L1, L2 정규화 일반화
정규화는 모델의 파라미터 (즉 학습을 통해 찾고자 하는 값들 - 회귀의 경우 θ)에 대한 손실 함수를 최소화 하는 모든 알고리즘에 적용할 수 있습니다. 따라서 다중 회귀, (다중) 다항 회귀, 로지스틱 회귀 모델 모두에 정규화를 적용할 수 있는데요. 그냥 모델에 해당하는 손실 함수에 정규화 항
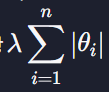
또는
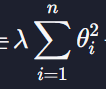
를 더해주면 된다
물론 scikit-learn같은 라이브러리를 사용해서 실제로 모델을 만들 때는 알아서 정규화를 적용해 주는 모델을 사용하면 되는데요. 다중 회귀 또는 다항 회귀 모델을 만들 때는 LinearRegression 대신 Lasso (L1 정규화) 또는 Ridge (L2 정규화) 모델을 사용하면 됩니다.
그렇다면 로지스틱 회귀 모델을 구현한 LogisticRegression에 정규화를 적용하고 싶으면 어떻게 해야할까??
사실 이 모델은 자동으로 L2정규화를 적용한다 -> 정규화를 적용하도록 따로 모델을 안바꿔줘도 된다
어떤 정규화 기법을 사용할지는 모델의 penalty라는 파라미터로 정해줄 수 있다
LogisticRegression(penalty='none') # 정규화 사용 안함
LogisticRegression(penalty='l1') # L1 정규화 사용
LogisticRegression(penalty='l2') # L2 정규화 사용
LogisticRegression() # 위와 똑같음: L2 정규화 사용그리고 딥러닝을 배울 때도 정규화는 아주 중요하다
딥러닝 모델의 파라미터는 세타가 아닌 w로 나타낸다
그래서 손실함수에 정규화 항
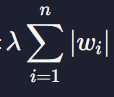
또는
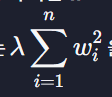
2.10 L1, L2 정규화 차이점
-
L1 정규화는 여러 θ값들을 0으로 만들어 줍니다. 모델에 중요하지 않다고 생각되는 속성들을 아예 없애주는 거죠.
-
L2 정규화는 θ값들을 0으로 만들기보다는 조금씩 줄여 줍니다. 모델에 사용되는 속성들을 L1처럼 없애지는 않는 거죠.
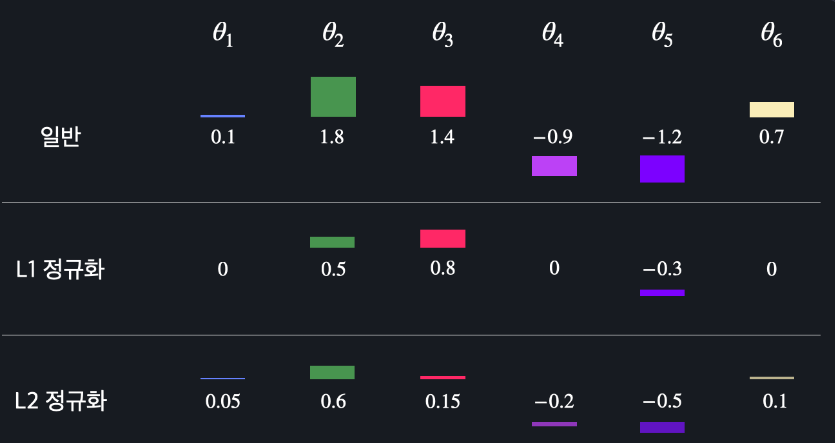
-> L1 정규화는 어떤 모델에 쓰이는 속성 or 변수의 개수를 줄이고 싶을 때 사용
ex) 속성 20개를 사용해서 2차 다중 다항 회귀 모델을 만든다 -> 속성 = 230개

이렇게 속성이 많으면 좋지 않음 -> L1 정규화 사용 -> 많은 θi를 0으로 만들어줘서 속성의 개수를 많이 줄일 수 있다
예시 )
L1 손실함수
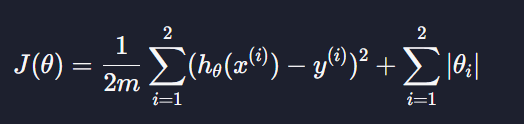
θ0은 정규화 항에 안 포함 되니까 상수로 가정, 정규화 항에 곱하는 상수는 λ=1 이라고 가정
최소화 기법을 활용해서 손실함수를 최소화하는 (θ1,θ2) = (a,b) 를 찾았다고 하고 정규화 항의 값은 어떤 숫자 t라고 하면 L1 손실 함수를 최소화하는 θ값들은 θ1 도는 θ2가 0일 확률이 높다는게 보일 것이다
-
θ1과 θ2에 대한 평균 제곱 오차 그래프

ㄴ 어떤 최소점이 있고 최소점에서 멀어질 수록 평균 제곱 오차가 커지는 모습 -
θ1과 θ2에 대한 정규화 항의 값 그래프 (정규화 항의 값이 t)
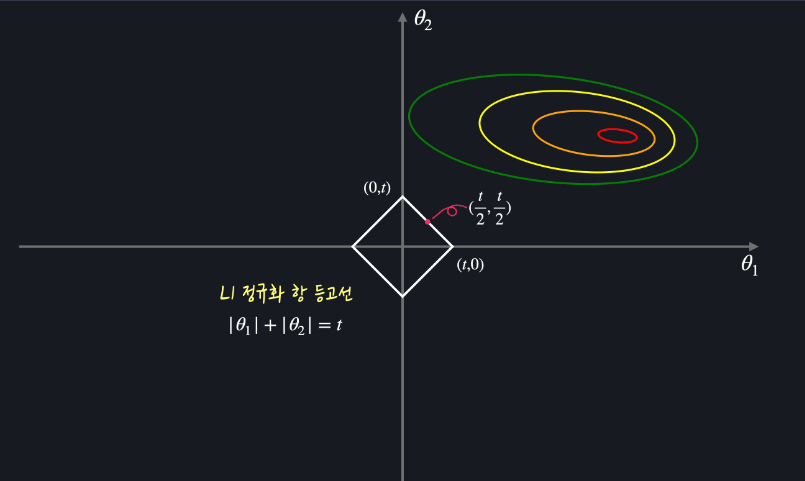
ㄴ 우리가 찾은 최적값(a,b)도 이 등고선 위에 있을텐데, 정규화 항의 값이 t로 고정돼있다면 손실을 최소화하기 위해 평균 제곱 오차만 최소화하면 된다
ㄴ 평균 제곱 오차를 최소화 하는 방법 : 평균 제곱오차의 등고선이 마름모에 닿을 때 까지 조금씩 더 큰 등고선을 그려주면 됨
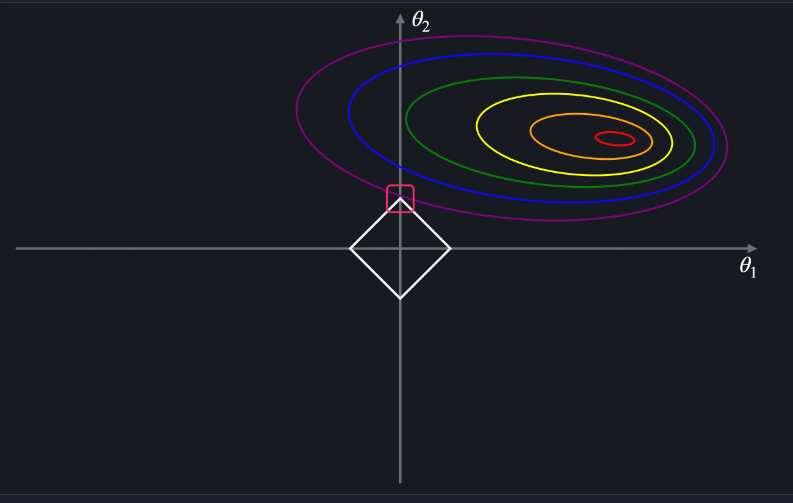
마름모에 닿는 지점에 해당하는 θ1은 0, θ2는 t 이다 = (a,b) = (0,t)
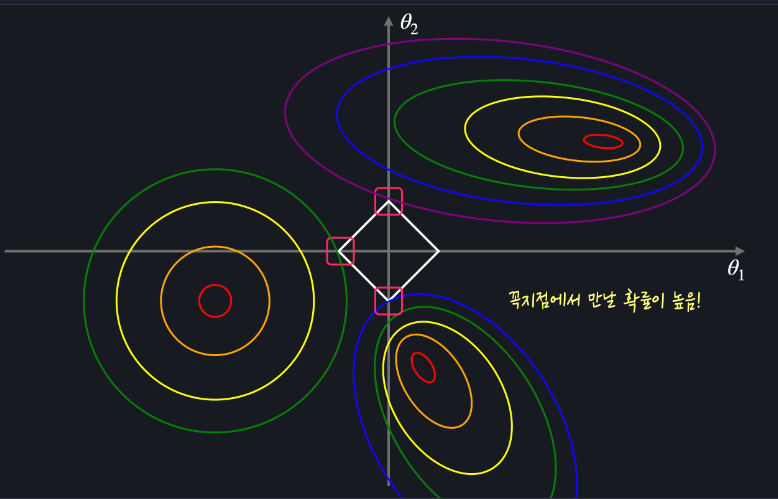
t의 값이 어떻고 평균 제곱 오차의 그래프가 어떻게 생겼든 마름모와 평균 제곱 오차의 등고선이 닿는 지점은 꼭짓점일 확률이 높다 = θ1 또는 θ2 가 0이라는 뜻
- L2정규화
L2의 손실함수
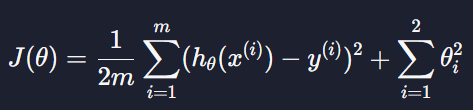
L2 정규화 항 등고선 (θ1^2 + θ2^2 = t)
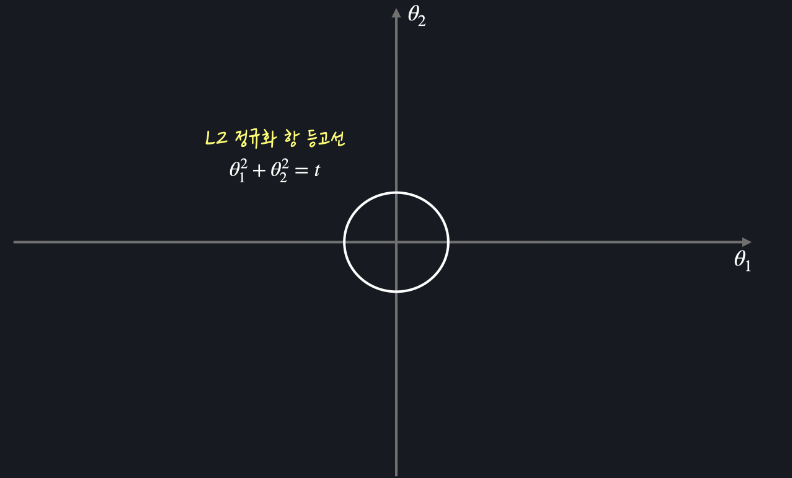
마름모 모양과 다르게 원모양 등고선은 평균 제곱 오차의 등고선과 닿는 지점이 축 위가 아닐 확률이 높다
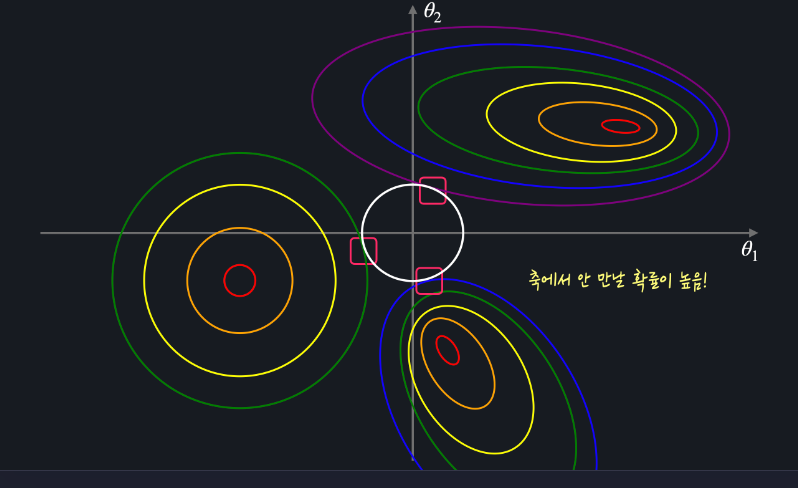
= L2 손실 함수를 최소화 하는 θ1, θ2 값은 둘 다 0이 아닐 확률이 높다
정리 !
L1 손실 함수를 최소화하는 θ는 여러 θi가 0일 확률이 높고, L2 손실 함수를 최소화하는 θ는 모든 θi가 0이 아닐 확률이 높습니다.
