[Inception-v3] Rethinking the Inception Architecture for Computer Vision

안암동컴맹·2026년 1월 7일

Paper Review

목록 보기

5/12

🤗 소개

이 글은 Szegedy et al.(2015)의 Rethinking the Inception Architecture for Computer Vision 을 원 논문이 실제로 전개하는 흐름(Introduction → General Design Principles → Factorizing Convolutions → Auxiliary Classifiers → Efficient Grid Reduction → Inception-v2/v3 구성 → Label Smoothing → Training → Low-resolution input 실험 → Experimental Results → Conclusions)을 최대한 그대로 따라가며 상세히 분석한 리뷰이다.

이 논문은 2014년 GoogLeNet(Inception-v1) 이후 Inception 계열을 한 번 더 밀어붙인다. 포인트는 단순히 더 깊게가 아니라, 추가 계산을 최대한 효율적으로 쓰는 방식으로 네트워크를 스케일업하는 것이다. 핵심 도구로는

큰 커널 합성곱을 더 작은 합성곱의 조합으로 factorization 하기
1×1 합성곱을 차원 축소/확장에 적극적으로 써서 병목(bottleneck) 을 피하기
grid size를 줄일 때 표현 병목이 생기지 않게 grid reduction 블록을 설계하기
보조 분류기(auxiliary classifier)를 최적화 가속용이 아니라 regularizer로 재해석하기
라벨 스무딩(label smoothing)으로 분류기를 덜 확신하도록 만들어 일반화를 높이기

같은 설계가 묶여 있다.

논문은 정량적으로도 매우 강한 수치를 제시한다. ILSVRC 2012 validation에서, 단일 모델(single frame) 기준 top-1 error 21.2%, top-5 error 5.6%를, 그리고 4개 모델 앙상블 + multi-crop에서 top-5 error 3.5%까지 보고한다. 또한 모델은 inference 당 5 billion multiply-adds 정도의 연산 비용으로, 파라미터 수는 25M 미만이라고 말한다.

1️⃣ 배경 상황

🔹 AlexNet 이후의 큰 흐름

논문은 AlexNet 이후 CNN이 object detection, segmentation, pose estimation, video classification 등 광범위한 비전 문제에 성공적으로 적용되면서, 더 높은 성능의 아키텍처를 찾는 연구가 빠르게 확산되었다고 말한다. 2014년에는 VGGNet과 GoogLeNet이 ILSVRC에서 비슷한 수준의 높은 성능을 보였고, 중요한 관찰로서 분류 성능의 개선이 다른 작업으로도 잘 전이된다고 강조한다. 즉 좋은 아키텍처를 만들면, 단일 과제에 그치지 않고 비전 전반의 표현 품질이 올라간다는 이야기다.

여기서 VGGNet과 GoogLeNet을 대비시키는 메시지는 다음처럼 정리된다.

VGGNet: 구조가 단순하지만 계산 비용이 매우 크다.
GoogLeNet(Inception-v1): 메모리/연산 예산이 제한된 상황에서도 좋은 성능이 나오도록 설계되었다.
- 파라미터 수가 5M 수준으로 AlexNet(60M) 대비 12× 적었다.

이 논문은 이 효율성 관점을 유지한 채로, Inception 계열을 더 확장하면서도 계산을 낭비하지 않도록 하는 설계로 들어간다.

🔸 이 논문이 말하는 스케일업의 목표

큰 모델은 보통 성능을 올리지만, 계산 비용과 파라미터 증가는 현실 제약(특히 모바일/대규모 서비스)과 충돌한다. 그래서 이 논문은 다음을 목표로 한다.

더 큰 계산을 쓰더라도, 그 계산이 실제 성능 향상으로 이어지도록 아키텍처를 구성한다.
큰 커널을 그대로 쓰는 대신, 연산/파라미터 효율이 좋은 형태로 쪼개서 사용한다.
규제(regularization)도 구조적으로 설계해 일반화 성능을 더 안정적으로 끌어올린다.

2️⃣ 일반적인 디자인 원칙

🔹 초반에서 Representative Bottleneck 피하기

논문은 feed-forward 네트워크를 입력에서 출력으로 흐르는 DAG로 보고, 입력과 출력을 나누는 임의의 cut을 생각했을 때 그 cut을 통과하는 정보량을 직관적으로 떠올릴 수 있다고 말한다. 핵심은 극단적인 압축을 조심하라는 것이다.

여기서 중요한 뉘앙스는 다음과 같다.

표현 차원(dimensionality)이 정보량의 정확한 측정치는 아니다(상관 구조 등 때문에).
하지만 차원은 대략적인 정보량의 상한 및 구조를 주므로, 과도한 차원 축소는 위험 신호다.
일반적으로 입력에서 출력으로 갈수록 표현 크기가 완만하게 감소해야 하며, 마지막 task representation으로 갈 때만 충분히 줄어들면 좋다.

이 원칙은 뒤에서 grid size를 줄일 때의 블록 설계로 직결된다.

🔸 고차원 표현은 로컬 처리가 쉬움

논문은 동일한 공간 타일(tile)에서 더 많은 activation을 유지하면 더 disentangled feature를 만들기 쉽고, 그 결과 네트워크가 더 빨리 학습된다고 말한다. 즉 표현력을 키우고 싶다면, 무조건 공간 해상도를 키우는 것만이 아니라 채널 차원에서 충분히 넓은 표현을 주는 것도 중요한 스케일업 방식이라는 이야기다.

Inception-v3에서 coarsest grid(8×8)에서 채널을 크게 늘리는 설계가 이 원칙과 연결된다.

🔹공간 집계는 낮은 차원 임베딩 위에서도 가능

인접 activation들이 강하게 상관되어 있다면, 공간적으로 퍼진 집계(예: 3×3 conv)를 하기 전에 채널 차원을 줄여도 표현력이 크게 깨지지 않을 수 있다고 논문은 주장한다. 이는 GoogLeNet이 1×1 reduction을 통해 병목을 제거하고 계산을 절약했던 핵심 아이디어를, 더 넓은 범위로 일반화한 것이다.

즉 1×1 reduction은 단순한 트릭이 아니라, 인접 신호가 쉽게 압축된다는 가정(강한 상관)을 전제로 하는 설계 원칙으로 읽을 수 있다.

🔸 Depth와 Width를 균형적으로 늘리기

고정된 연산 예산에서 성능을 올리려면, width만 키우거나 depth만 키우는 것보다 둘을 함께 늘리는 것이 더 낫다고 논문은 주장한다. 즉 자원 분배 관점에서 stage별 필터 수와 네트워크 깊이를 균형 있게 조절해야 한다는 것이다.

논문은 이 원칙들이 그럴듯하지만, 실제로는 애매한 상황에서만 지침으로 쓰는 것이 좋다고 말한다. 즉 원칙은 절대 법칙이 아니라, 설계 과정에서 문제 상황을 감지하고 수정하는 기준에 가깝다.

3️⃣ 큰 필터 사이즈를 통한 Conv Factorization

🔹 Factorization의 중요성

논문은 Inception 네트워크가 fully convolutional 구조이기 때문에, 각 weight는 activation마다 곱셈 하나에 대응하며, 계산량 감소는 곧 파라미터 감소로 직결된다고 말한다. 즉 factorization으로 계산을 줄이면

모델이 더 작아지고
파라미터가 더 분해되어(disentangled) 학습이 쉬워질 수 있고
절약한 예산으로 다른 곳(필터 뱅크 크기 등)에 자원을 재배치할 수 있다.

이 관점은 이후의 5×5 → 3×3+3×3, 3×3 → 3×1+1×3, 7×7 → 1×7+7×1 같은 구체 설계로 이어진다.

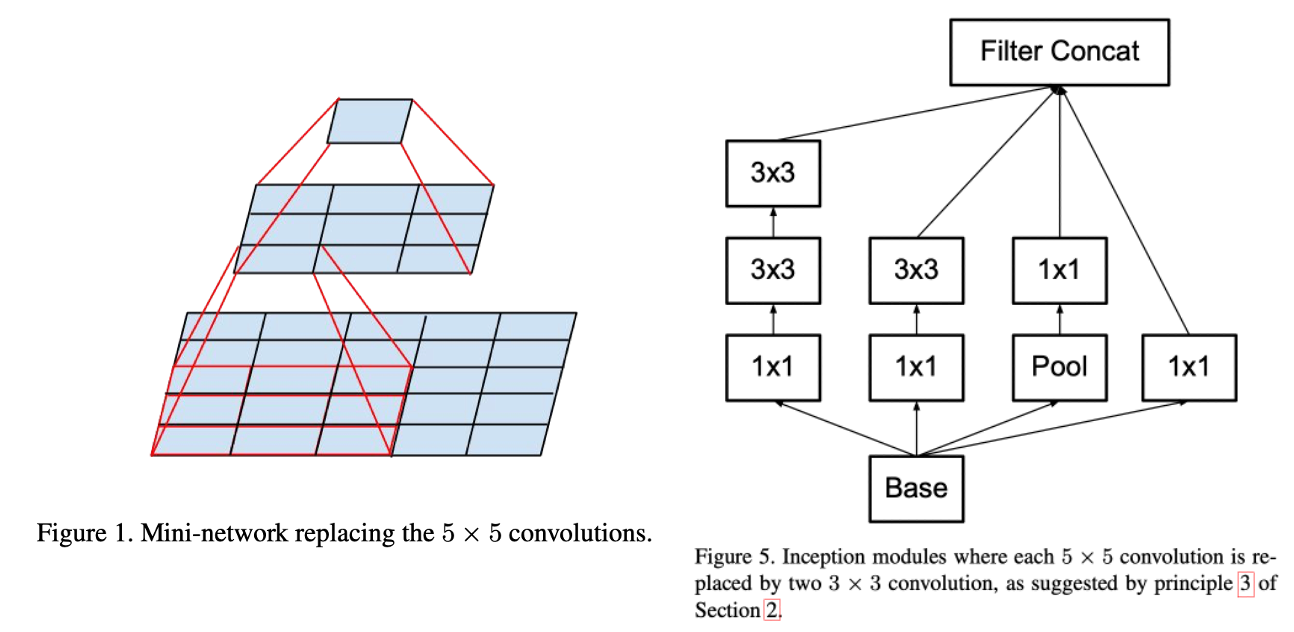
🔸 더 작은 합성곱 연산들로 분해

큰 커널 합성곱은 비싸다. 논문은 5×5 conv가 3×3 conv보다 같은 입력/출력 채널일 때 계산 비용이

\frac{25}{9} \approx 2.78

배라고 말한다.

하지만 5×5의 receptive field가 주는 표현력은 중요한데, 커널 크기를 줄이면 표현력이 줄 수 있다. 논문은 여기서 질문을 던진다.

"5×5 conv 하나를, 더 적은 파라미터를 갖는 다층 네트워크로 대체할 수 없을까?"

논문은 5×5 conv의 계산 그래프를 보면, 사실상 5×5 타일 위에서 작은 fully-connected 네트워크가 슬라이딩하는 것과 같다고 보고, translation invariance를 다시 이용해 이를 두 층의 conv로 대체하는 설계를 제안한다.

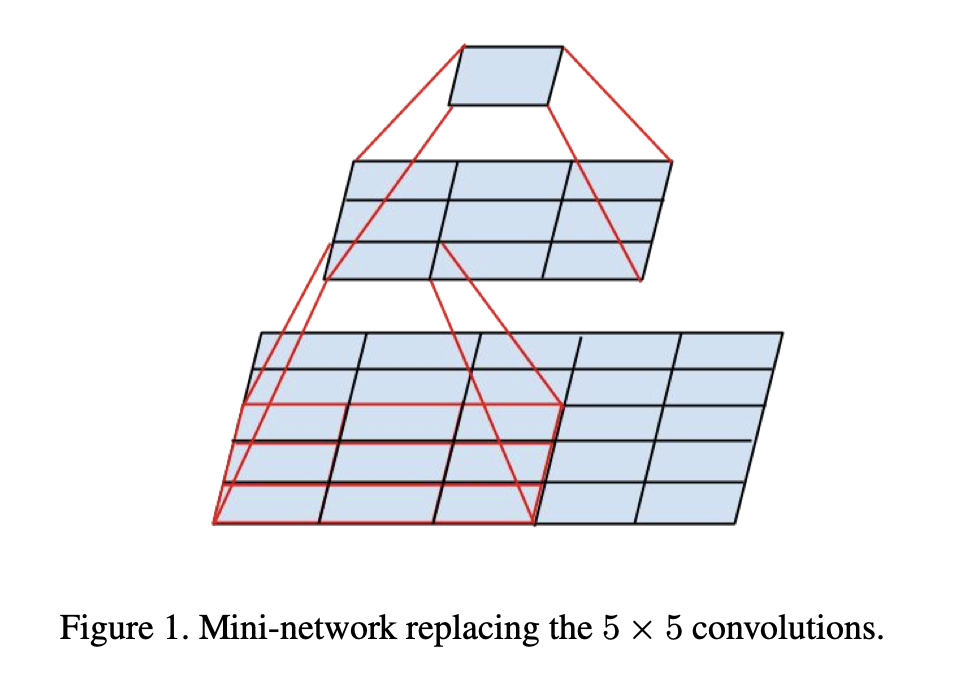
즉 다음과 같은 대체가 나온다.

원래: 5×5 conv
대체: 3×3 conv → 3×3 conv

두 3×3을 쌓으면 effective receptive field는 5×5가 된다. 중요한 점은, 이 대체는 단순히 5×5를 쪼개는 게 아니라 중간에 비선형성(ReLU, BN 등) 을 넣을 수 있어 표현력이 오히려 좋아질 여지가 있다는 것이다.

논문은 단순화된 계산에서, 5×5를 3×3 두 번으로 바꾸면 계산이

\frac{9 + 9}{25} = \frac{18}{25}

로 줄어들어 약 28% 절감된다고 말한다. 파라미터 수 절감도 동일하게 적용된다고 설명한다.

선형 활성화 vs ReLU

만약 우리가 선형 부분을 factorize하려는 것이라면, 첫 번째 3×3 뒤를 선형으로 두는 게 더 자연스럽지 않냐는 질문이 가능하다. 논문은 이 점을 직접 실험한다.

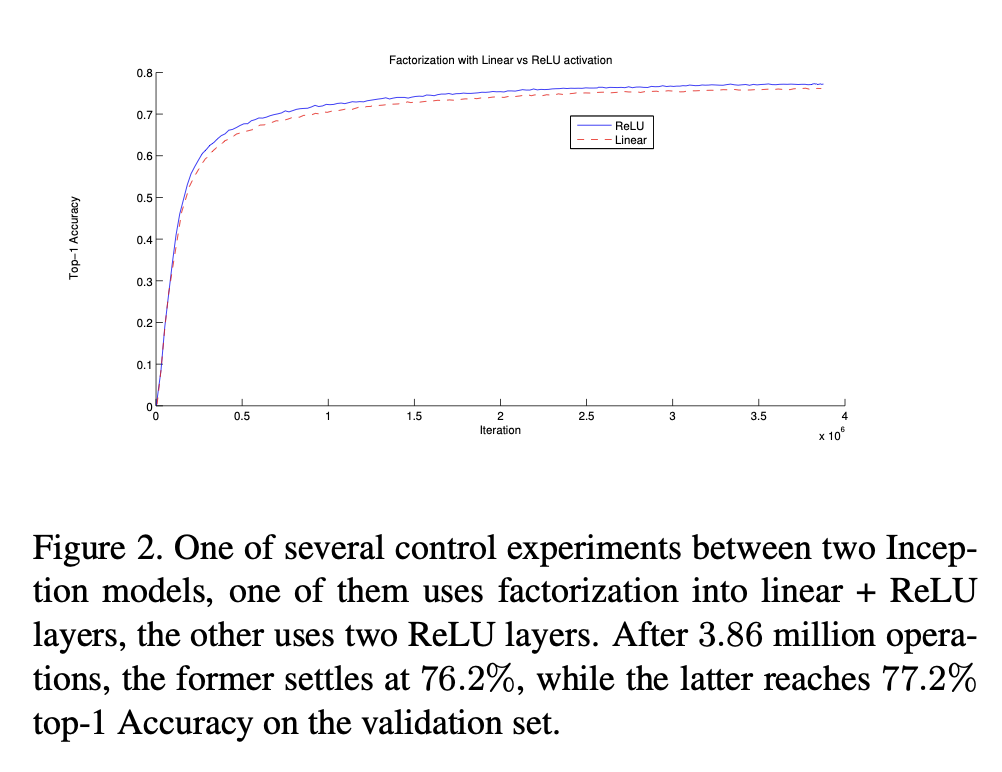
결론은 일관되게 ReLU를 모든 단계에 두는 것이 더 좋았고, BN을 넣을 때 특히 그 효과가 커졌다고 말한다. 즉 factorization은 단순한 선형 분해가 아니라, 비선형을 더 많이 넣는 구조적 설계로 이해하는 편이 맞다.

🔹 Spatial Factorization을 비대칭 Conv로

논문은 3×3도 2×2 두 번으로 줄일 수 있겠지만, 더 좋은 방법이 있다고 말한다. 바로 asymmetric(비대칭) conv를 쓰는 것이다.

3×1 conv → 1×3 conv

이 조합은 receptive field 관점에서 3×3과 동등한 범위를 커버하면서도, 같은 입력/출력 채널 수일 때 계산 비용이 더 낮다. 논문은 3×3을 3×1+1×3으로 바꾸면 33% 절감, 3×3을 2×2+2×2로 바꾸면 11% 절감이라고 비교한다.

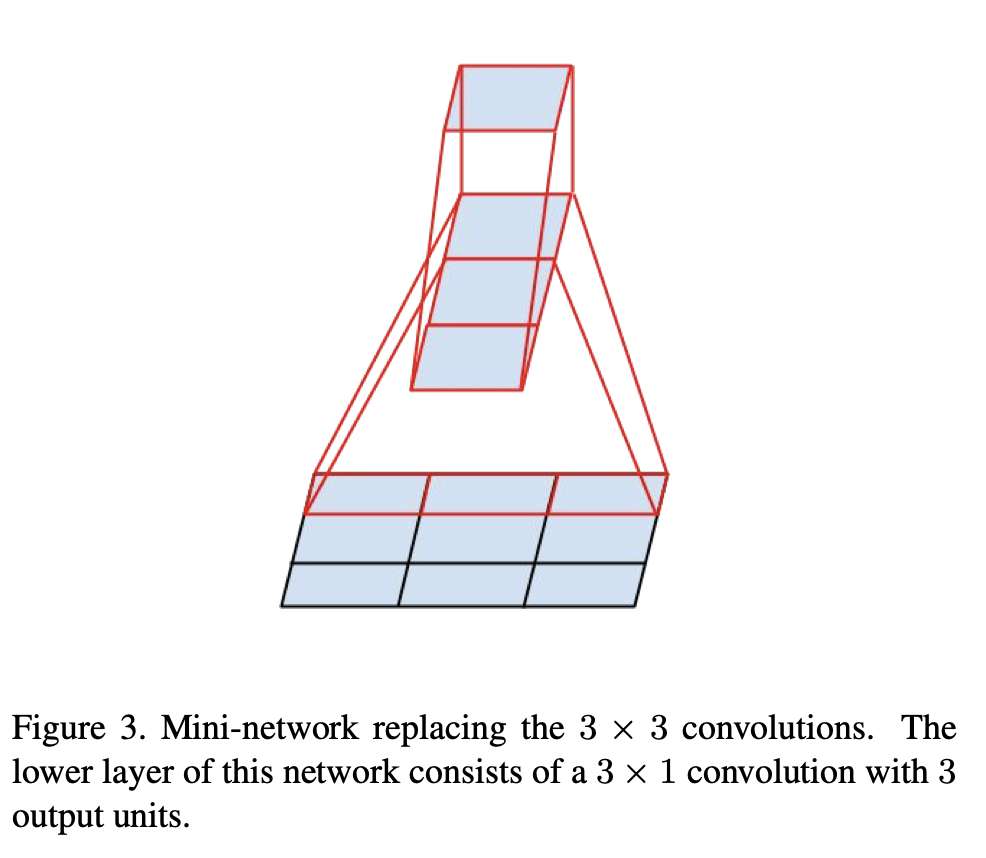
이 아이디어를 일반화하면, n×n conv를 1×n + n×1로 바꿀 수 있다. n이 커질수록 절감 폭도 커진다.

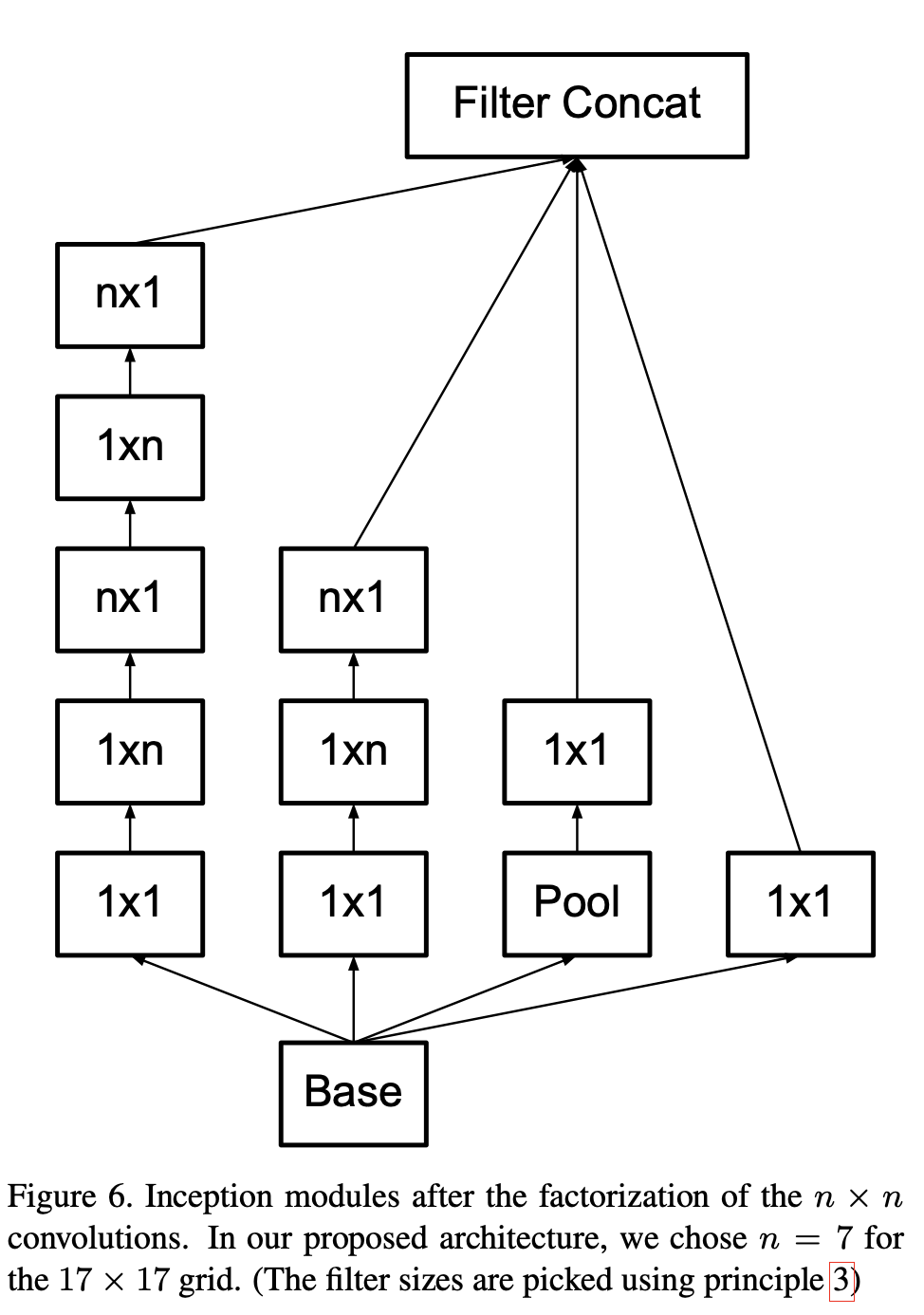
논문은 이 factorization이 초반 레이어에서는 잘 안 먹히지만, 중간 grid size(약 12~20)에서는 매우 잘 동작했으며, 구체적으로 17×17 grid에서는 1×7 + 7×1이 좋은 결과를 줬다고 말한다.

4️⃣ 보조 분류기의 활용

🔹 GoogLeNet(v1)에서의 가설과 이 논문의 관찰

GoogLeNet(v1)은 깊은 네트워크에서 vanishing gradient를 완화하기 위해 보조 분류기를 도입했다. 즉 중간 레이어에 side head를 달아, 하위 레이어에 더 직접적인 gradient를 전달해 학습을 가속한다는 가설이다.

하지만 이 논문은 실험적으로 다른 관찰을 보고한다.

학습 초반에는 보조 분류기 유무에 따른 수렴 속도 차이가 거의 없다.
학습 후반부에서 보조 분류기가 있는 모델이 조금 더 좋은 plateau에 도달한다.

즉 보조 분류기는 최적화 가속이라기보다는, 학습이 충분히 진행된 이후 일반화에 도움이 되는 방향으로 작동하는 것으로 해석할 수 있다.

또한 v1에서 2개의 side head를 쓰던 것과 달리, 더 낮은(aux lower) 분류기를 제거해도 성능에 악영향이 없었다고 말한다.

🔸 Regularizer 역할의 보조 분류기

논문은 보조 분류기가 regularizer로 작동한다는 근거로 다음을 든다.

보조 분류기의 main classifier 성능은, side head가 BN을 포함하거나 dropout이 있을 때 더 좋아진다.
특히 side head의 BN이 top-1 accuracy를 0.4%p 올렸다고 보고한다.

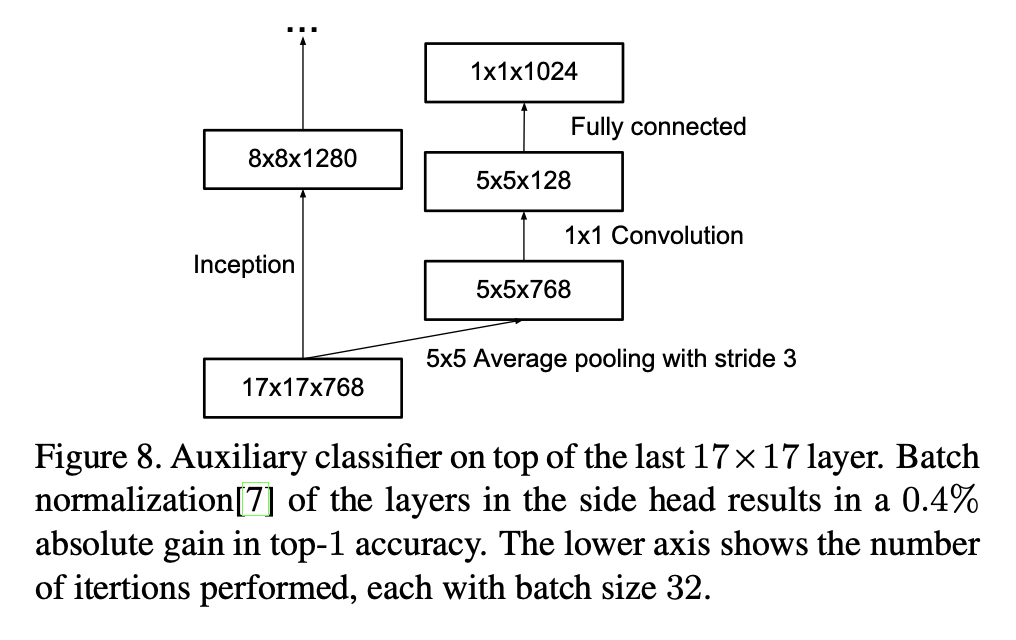
이 관찰은 BN이 regularizer 역할도 한다는 weak evidence로 연결된다.

5️⃣ 효율적인 Grid Size 감소

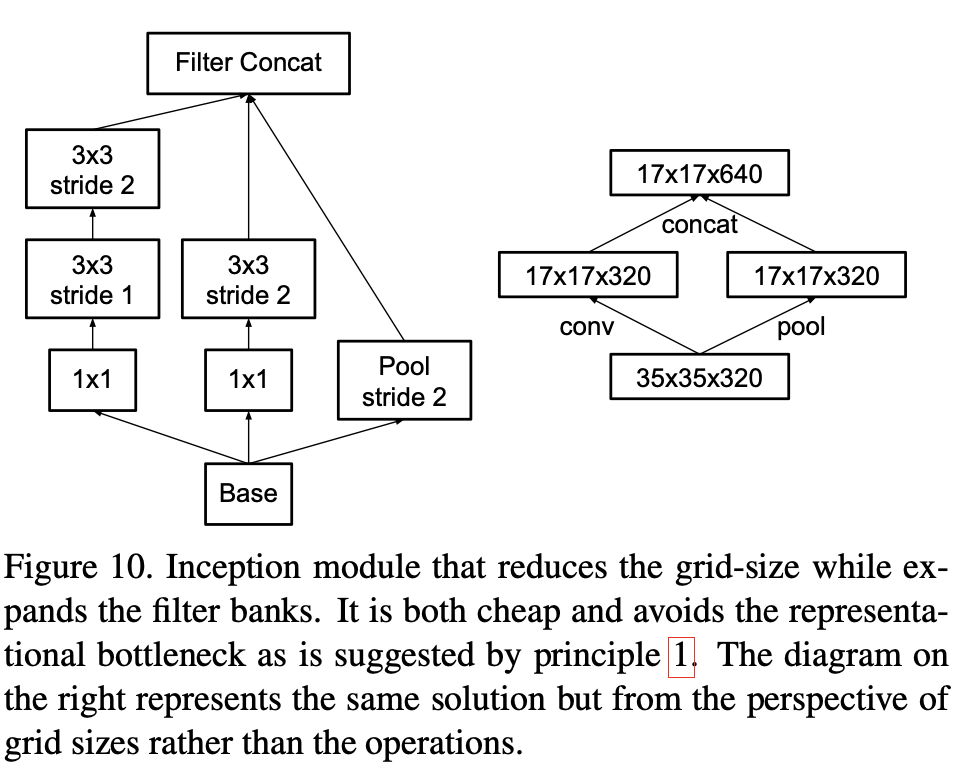
🔹 Grid Reduction에서 발생하는 문제

전통적으로 feature map의 grid size(H×W)를 줄일 때 pooling 을 사용한다. 하지만 표현 병목을 피하려면 pooling 전에 채널 수를 늘리는(expand) 것이 일반적이다. 논문은 이를 정량적으로 설명한다.

$d×d$ grid에서 $k$ 채널을 갖는 feature map을, $d/2×d/2$ grid에서 $2k$ 채널로 만들고 싶다고 하자. 병목 없이 가려면 대략 다음이 필요하다.

stride 1 conv로 $2k$ 채널을 먼저 만들고
pooling으로 $d/2×d/2$ 로 줄인다

그러면 계산은 큰 grid에서 $2k$ 채널을 만드는 conv가 지배하고, 대략 $\mathcal{O}(2d^2k^2)$ 형태로 비싸진다.

그렇다고 그냥 pooling과 conv를 섞어 stride 2로 내려버리면 계산은 줄지만, 표현 차원이

d \times d \times k \;\;\to\;\; \frac{d}{2}\times \frac{d}{2} \times 2k

가 되어 전체 표현 크기(타일 수 × 채널 수)가 줄어들어 병목이 생길 수 있다.

이에 대한 해결책으로 논문은 grid reduction의 두 가지 naive한 대안을 아래 그림으로 보여준다.

하지만 위 그림에서 나타나듯이, 병목을 피하려고 하면 계산이 크게 증가하고, 계산을 줄이면 병목이 생기는 딜레마가 있다.

🔹 병렬 stride 2 경로 + concat으로 병목 회피

논문은 이 딜레마를 해결하기 위해, grid reduction 자체를 Inception처럼 병렬 구조로 만든다.

경로 P: pooling(stride 2)
경로 C: conv(stride 2) 경로(여러 conv 조합)
두 경로의 출력 채널을 concat해 다음 스테이지로 넘긴다

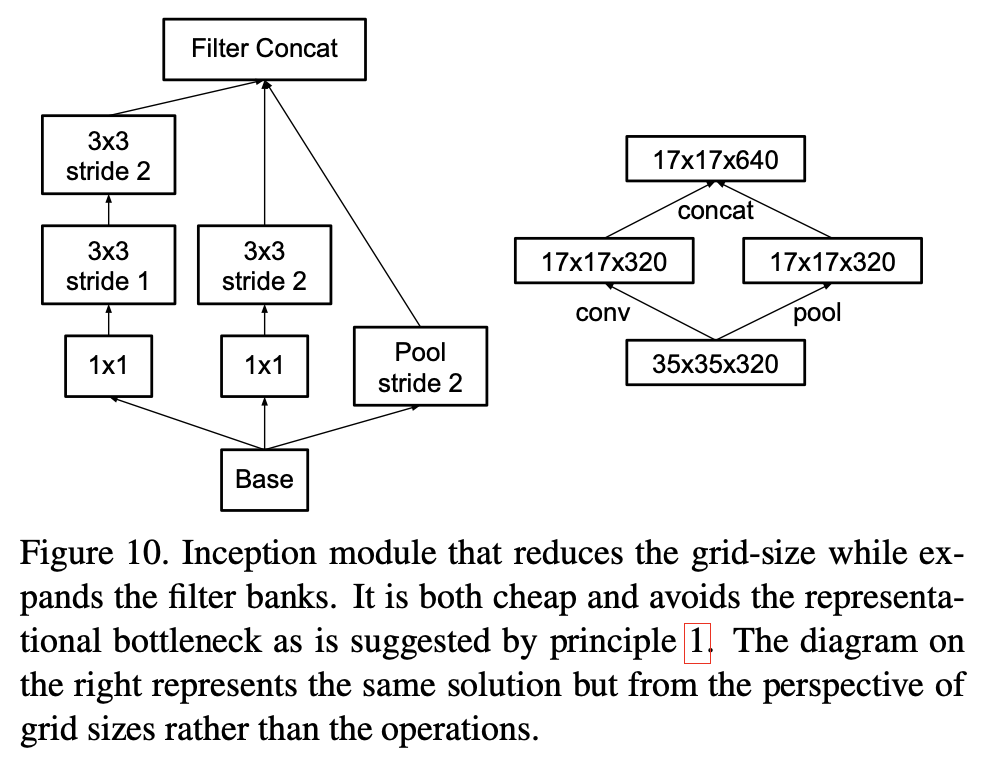
핵심은 grid가 줄어드는 순간에 채널을 충분히 늘리되, 그 증가를 한 번의 비싼 conv로 하지 않고 병렬 경로로 분산시켜 계산 효율을 유지한다는 것이다.

6️⃣ Inception-v2 / Inception-v3

🔹 전체 네트워크 개요

논문은 앞에서 소개한 요소들을 모아 새로운 네트워크를 제안한다. 전체 아키텍처 개요는 아래 도표에 제시된다.

표의 큰 흐름을 텍스트로 재구성하면 다음과 같다.

Stem: 초기 conv/pool로 299×299를 35×35 수준으로 줄이면서 채널을 만든다
35×35 스테이지: 전통적인 Inception 모듈을 3번 쌓는다(논문은 Fig. 5 계열을 언급)
grid reduction: 35×35 → 17×17(sect. 5의 기법)
17×17 스테이지: factorized Inception 모듈을 5번 쌓는다(Fig. 6의 n×n factorization, 여기서는 n=7을 선택했다고 설명)
grid reduction: 17×17 → 8×8(Fig. 10 기법)
8×8 스테이지: 고차원 표현을 위해 확장된 모듈(Fig. 7)을 2번 쌓는다. 각 타일당 출력 filter bank가 2048이 되도록 설계한다.
마지막: 8×8에서 global pooling을 거쳐 1×1×2048, linear, softmax로 분류

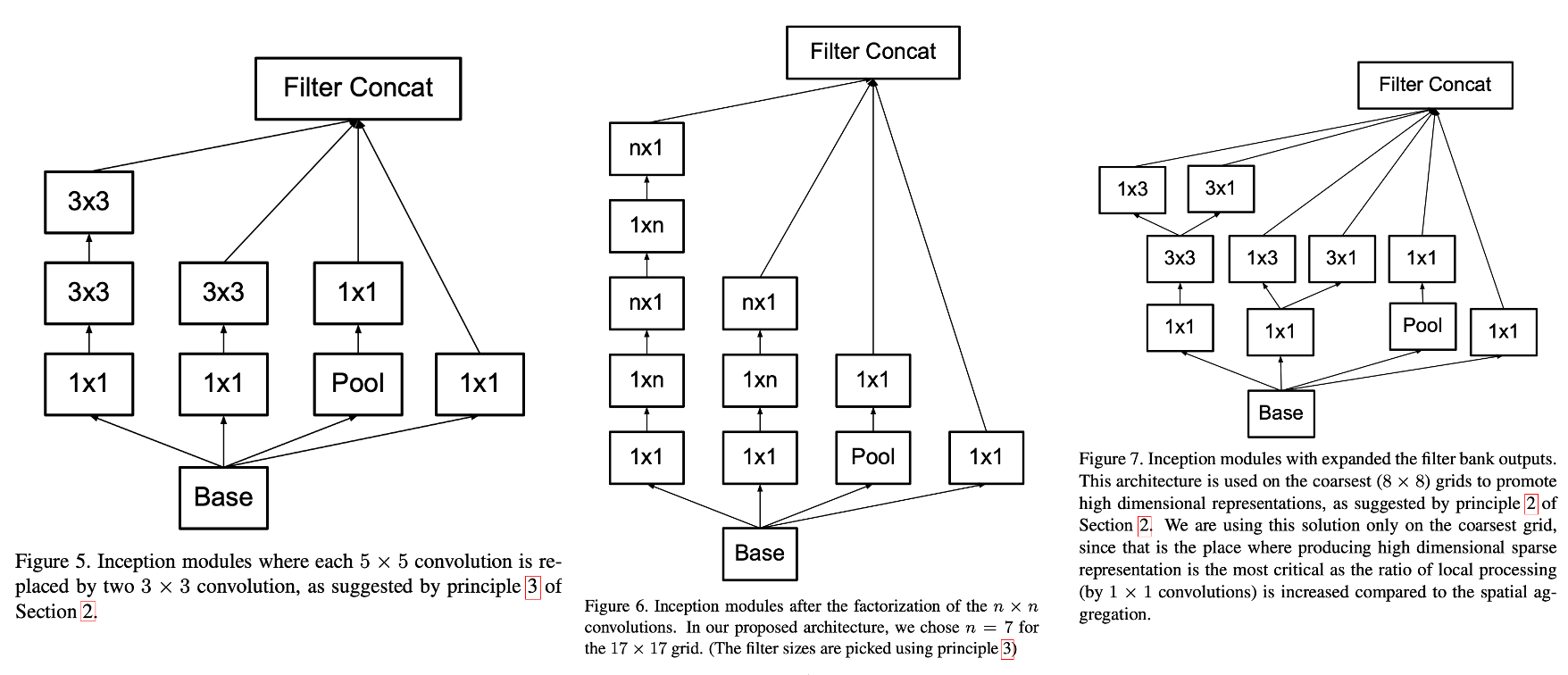
논문은 네트워크가 42 layers deep라고 말하며, 계산 비용은 GoogLeNet 대비 2.5× 정도이지만 VGGNet보다는 훨씬 효율적이라고 주장한다.

🔸 Inception-v2와 Inception-v3의 관계

논문 본문에서 Inception-v2는 제안 아키텍처의 누적 개선 과정(각 섹션의 변경 사항을 계속 적용한 결과)을 가리키는 이름으로 쓰이고, 최종적으로 모든 변경을 반영한 모델을 Inception-v3라고 부르는 흐름으로 읽힌다.

이 구분은 (Table 3)에서 특히 중요하다. 표의 각 줄은 이전 변경 사항을 포함한 누적(cumulative) 결과이며, 마지막 줄의 모든 변경을 포함한 모델이 Inception-v3라고 명시된다.

7️⃣ Label Smoothing를 통한 모델 규제

🔹 Label Smoothing 기본 설정

Label smoothing을 설명하기 위해 논문은 먼저 표기를 정리한다.

클래스 수가 $K$ 일 때, 입력 $x$ 에 대해 모델이 로짓 $z \in \mathbb{R}^K$ 를 출력한다고 하자. softmax 확률은

p(k\mid x)=\frac{\exp(z_k)}{\sum_{i=1}^{K}\exp(z_i)}.

정답 분포를 $q(k\mid x)$ 라고 하고(합이 1), 크로스 엔트로피 손실을

\ell = -\sum_{k=1}^{K} q(k)\log p(k)

로 둔다. (여기서 $x$ 의존은 생략)

논문은 이 손실을 로짓에 대해 미분하면

\frac{\partial \ell}{\partial z_k}=p(k)-q(k)

가 되어 gradient가 $-1$ 과 $1$ 사이로 bounded된다고 말한다.

🔸 One-Hot Label이 만드는 문제

단일 정답 라벨 $y$ 를 갖는 분류에서는 보통

q(y)=1,\;\;\; q(k)=0\;\;(k\neq y)

인 one-hot 분포를 쓴다. 이때 크로스 엔트로피를 최소화하는 방향은 $z_y$ 가 다른 로짓보다 훨씬 커지도록 만드는 것이고, 이 과정에서 모델이 지나치게 확신하게 될 수 있다.

논문은 이로 인해 두 가지 문제가 생길 수 있다고 말한다.

과적합: 학습 데이터에 대해 정답 확률을 $1$ 로 만들었다고 일반화가 보장되진 않는다.
적응성 저하: 가장 큰 로짓과 나머지 로짓들의 차이가 커지면, bounded gradient 특성과 결합되어 모델이 덜 잘 적응할 수 있다.

🔹 Label Smoothing의 정의

논문은 고정 분포 $u(k)$ 와 smoothing 파라미터 $\varepsilon$ 를 정의하고, 정답 분포를 다음처럼 바꾼다.

q'(k\mid x) = (1-\varepsilon)\delta_{k,y} + \varepsilon u(k).

직관적으로는 다음과 같은 확률 과정이다.

일단 라벨을 GT $y$ 로 둔다.
확률 $\varepsilon$ 로 라벨을 $u(k)$ 에서 다시 샘플링해 바꾼다.

논문은 $u(k)$ 로 prior 분포를 쓰자고 제안하며, 실험에서는 uniform prior를 사용한다.

u(k)=\frac{1}{K}\;\;\Rightarrow\;\; q'(k)=(1-\varepsilon)\delta_{k,y}+\frac{\varepsilon}{K}.

ILSVRC 2012에서는 $K=1000$ , $\varepsilon=0.1$ 을 사용했고, top-1/top-5 error가 약 0.2%p 개선되었다고 보고한다.

🔸 손실의 또 다른 해석

논문은 $q'$ 를 쓰는 크로스 엔트로피가 다음처럼 분해된다고 말한다.

H(q',p) = (1-\varepsilon)H(q,p) + \varepsilon H(u,p).

즉 label smoothing은

정답 분포 $q$ 에 대한 loss와
prior 분포 $u$ 에 대한 loss

를 가중합으로 함께 최소화하는 것과 같다. $H(u,p)$ 는 $D_{KL}(u\Vert p)+H(u)$ 로도 쓸 수 있으며( $H(u)$ 는 상수), 결국 예측 분포 $p$ 가 prior에서 지나치게 멀어지지 않도록 제약을 거는 형태의 regularization으로 이해할 수 있다.

Label Smoothing 학습 의사코드

논문 정의를 그대로 절차로 정리하면 아래처럼 쓸 수 있다.

Algorithm: Label smoothing regularization (Sect. 7)
Inputs:
  - class count K
  - smoothing epsilon
  - prior distribution u(k) (paper uses uniform)
  - ground-truth label y
1) Construct softened label distribution:
     q'(k) = (1-epsilon)*1[k=y] + epsilon*u(k)
2) Compute cross entropy:
     L = -sum_k q'(k) * log p(k)
Output: L

8️⃣ 훈련 방법론

🔹 분산 학습 설정

논문은 학습을 TensorFlow 분산 시스템으로 수행했다고 한다.

replicas: 50
각 replica: NVidia Kepler GPU
batch size: 32
epochs: 100

즉 총 배치 처리량은 replica 수까지 고려하면 상당히 큰 분산 학습 환경이다.

🔸 Optimizer와 Gradient Clipping

논문은 초기에는 momentum을 썼지만, 최종적으로 가장 좋은 모델은 RMSProp을 사용했다고 말한다. 하이퍼파라미터는 다음이 명시된다.

RMSProp decay: 0.9
RMSProp epsilon: 1.0
learning rate: 0.045
decay schedule: 2 epoch마다 exponential rate 0.94로 감소
gradient clipping threshold: 2.0 (학습 안정화에 유용)
evaluation: 시간에 따른 파라미터 running average를 사용

이 섹션은 아키텍처만큼이나, 대규모 학습에서 안정적인 최적화 설정이 중요하다는 점을 보여준다.

학습 절차 의사코드

Algorithm: Training setup (Sect. 8)
1) Train for 100 epochs with batch size 32 on 50 GPU replicas
2) Use RMSProp (decay=0.9, epsilon=1.0)
3) Use lr=0.045 and decay it every 2 epochs by factor 0.94
4) Apply gradient clipping with threshold 2.0
5) Evaluate using running average of parameters

9️⃣ Experimental Results and Comparisons

🔹 Single Crop에서의 누적 개선과 Inception-v3의 정의

논문은 Table 3에서 누적 개선을 정리한다. 핵심은 다음이다.

각 줄은 이전 변경 사항을 포함한 누적 결과다.
마지막 줄의 모든 변경을 포함한 모델을 이후 Inception-v3로 부른다고 말한다.

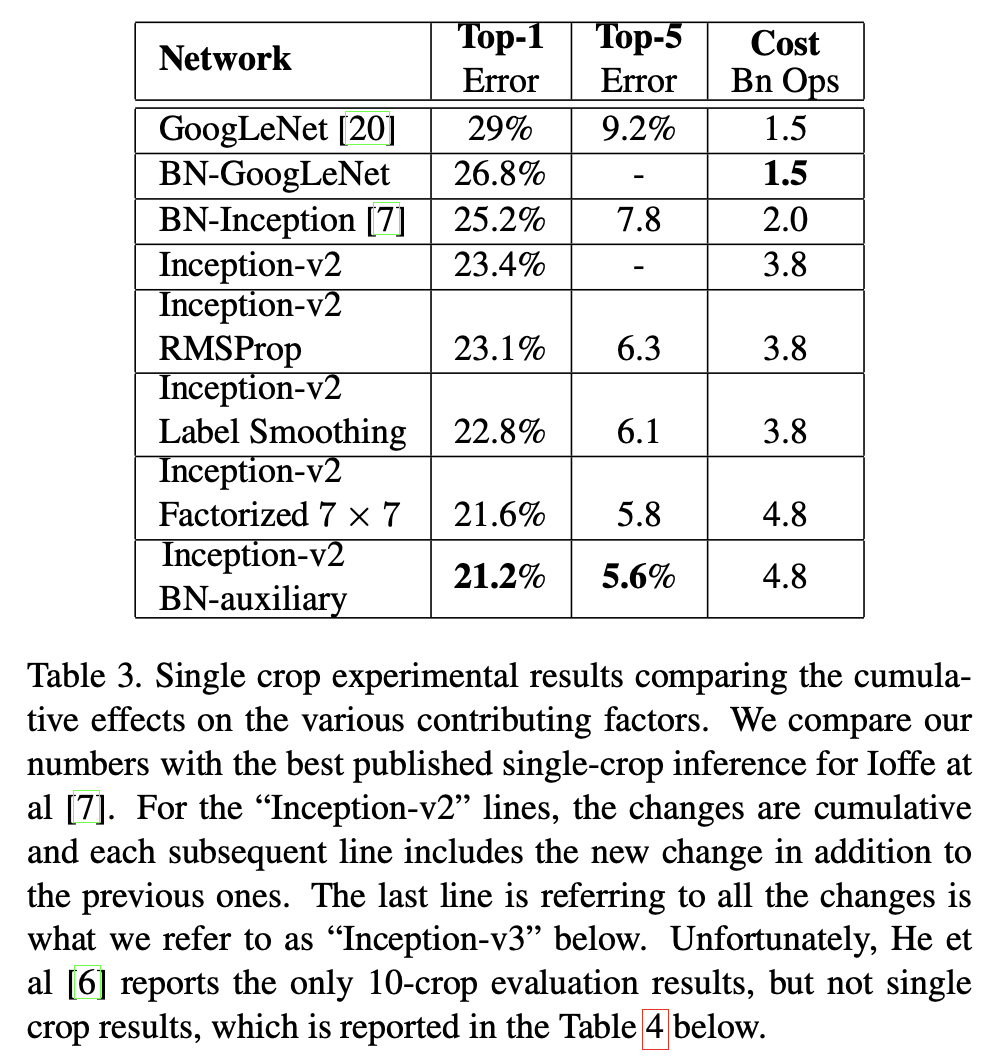
텍스트 추출본에서 표 정렬이 완전하지 않지만, 본문/표에서 읽히는 핵심 수치들은 다음과 같다.

GoogLeNet: top-1 error 29%, top-5 error 9.2%, cost 1.5Bn Ops
Inception-v2 계열로 개선이 누적되며 top-5 error가 5.8%까지 내려간다
최종 Inception-v3: top-1 error 21.2%, top-5 error 5.6%

여기서 Label Smoothing, Factorized 7×7, BN-auxiliary 같은 항목이 각각 개선을 더하는 요소로 등장하며, 각각이 0.2%p 단위의 개선을 만들었다는 식으로 해석할 수 있다.

🔸 Single-Model Multi-Crop에서의 비교

Table 4는 single-model에서 multi-crop을 적용했을 때의 성능을 비교한다. Inception-v3는 12-crop, 144-crop 평가를 보고한다.

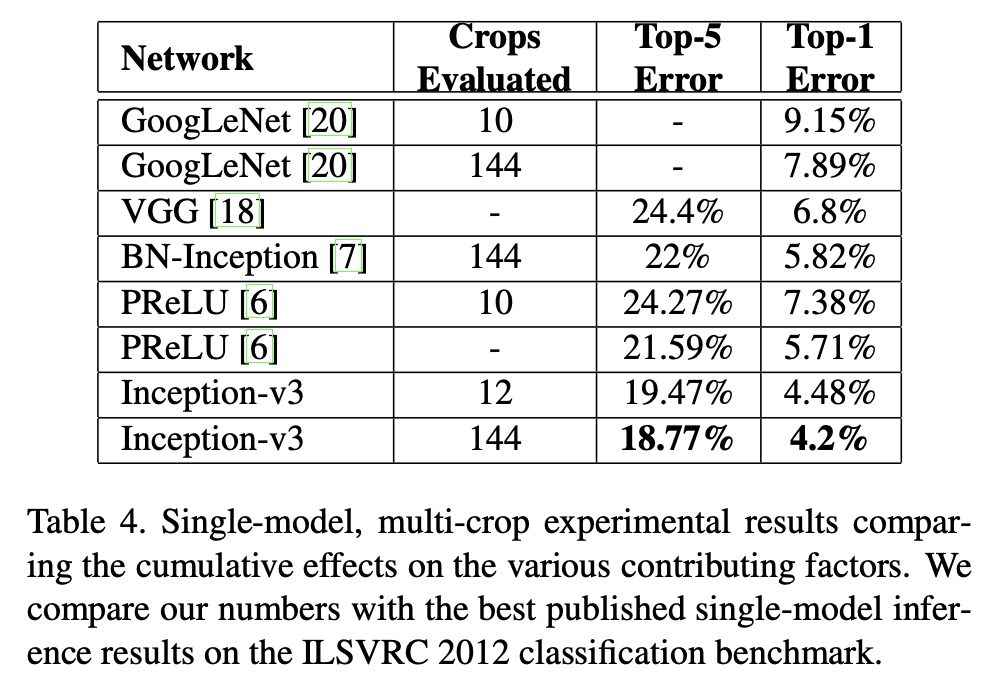
Network	Crops	Top-1 Error	Top-5 Error
Inception-v3	12	19.47%	4.48%
Inception-v3	144	18.77%	4.2%

즉 crop 수를 늘리면 좋아지지만, 증가폭은 점점 작아지는 형태다.

🔹 앙상블 결과

마지막으로 Table 5는 multi-model, multi-crop의 앙상블 비교를 제시한다.

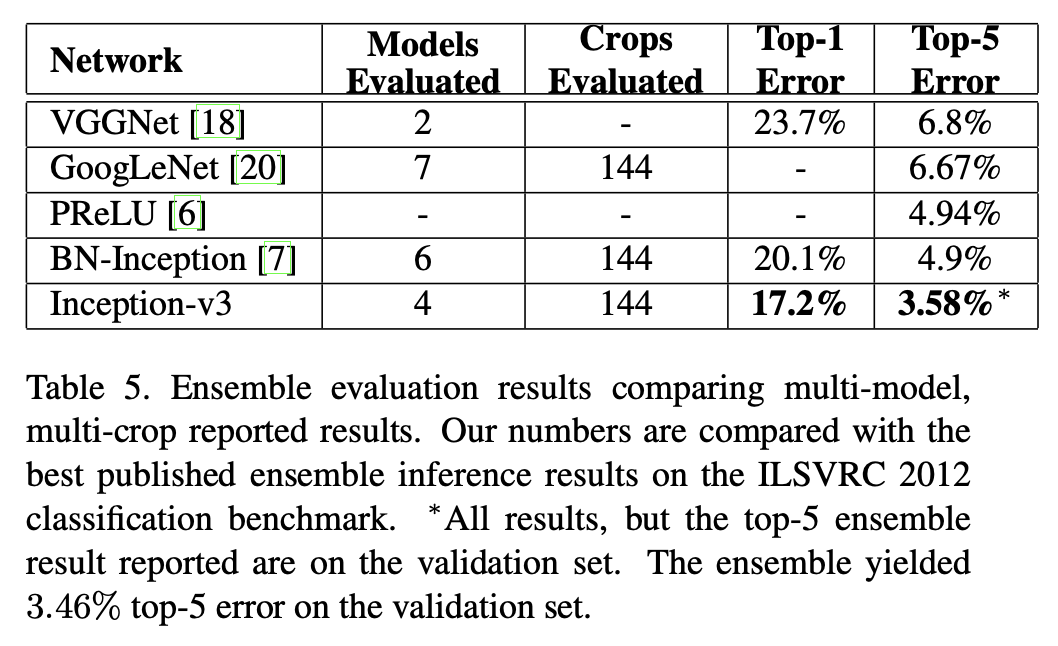
여기서 논문이 강조하는 핵심은 Inception-v3가 4개 모델 앙상블과 144-crop에서 top-5 error 3.58% 수준을 달성했고, validation에서 3.46%까지도 관찰되었다는 점이다. 이는 2014년 GoogLeNet 앙상블 대비 큰 상대 개선이라고 결론에서 다시 말한다.

🔟 실험에 대한 결론

🔹 원칙 기반 스케일업과 factorization/regularization의 결합

논문은 다음을 결론으로 정리한다.

Inception 아키텍처 맥락에서 네트워크를 스케일업하기 위한 설계 원칙들을 제시했고,
factorization과 aggressive dimension reduction을 통해 계산 효율을 유지하면서도 성능을 크게 올릴 수 있었고,
BN이 들어간 auxiliary classifier와 label smoothing 같은 regularization이 고품질 학습에 도움이 되었다.

또한 낮은 해상도의 receptive field에서도 좋은 결과가 가능하다는 점을 근거로, 작은 객체 분류 같은 문제에 응용 가능성을 언급한다.

마지막으로 성능 비교 관점에서, Inception-v3가 당시의 더 조밀한 네트워크 기반 방법들보다 훨씬 적은 계산/파라미터로도 더 낮은 error를 달성했다고 강조한다.

💡 해당 논문의 시사점과 한계

이 논문의 가장 큰 의의는 Inception 계열을 단순히 경험적 트릭 묶음이 아니라, 계산 예산을 어떻게 배치할지에 대한 설계 원칙 + 이를 구현하는 구체 블록들로 정리했다는 점이다.

Factorization의 관점 전환
5×5를 3×3 두 번으로, 3×3을 3×1+1×3으로, 7×7을 1×7+7×1로 바꾸는 방식은 단순한 계산 절감이 아니라, 비선형을 더 많이 주입해 표현력을 유지/증가시키는 구조적 설계로 제시된다.
병목 회피를 구조로 해결
grid reduction에서 생기는 병목 문제를 병렬 블록으로 해결하면서, 네트워크 전체에서 표현 크기가 급격히 줄지 않게 만든다. 이는 이후 많은 아키텍처에서도 반복되는 설계 감각이다.
Regularization을 아키텍처 수준으로 끌어올림
보조 분류기의 역할을 최적화 가속이 아니라 regularization으로 재해석하고, label smoothing을 수식으로 정리해 효과를 보인 점은 이후 분류기 학습의 표준 기법들로 이어졌다.

한계로는 다음을 짚을 수 있다.

논문은 많은 설계 원칙을 제시하지만, 스스로도 말하듯 원칙의 엄밀한 보편성은 확정적이지 않다. 즉 특정 작업/데이터/학습 세팅에서 유효한 경험 법칙으로 읽는 편이 안전하다.
본문에서 아키텍처의 세부 채널 구성은 supplementary에 의존하는 부분이 있고, 논문 자체만으로 완전 재현을 하려면 추가 자료 를 함께 봐야 한다.

그럼에도 이 논문은 Inception-v3라는 강력한 베이스라인을 제시하면서, 이후의 많은 모델 설계가 factorization, 병목 회피, 규제 기법 같은 키워드를 중심으로 전개되게 만든 중요한 기준점이다.

👨🏻‍💻 Inception-v3 구현하기

이 파트에서는 lucid라이브러리 내부의 inception.py 안의 Inception-v3 구현을 논문 관점으로 읽는다. Lucid에서는 Inception-v3를 inception_v3라는 팩토리 함수로 노출하며, 실제 모델 클래스는 Inception_V3다.

논문에서 Inception-v3는 다양한 factorization(예: 5×5 대체, 7×7 factorization), grid reduction, auxiliary classifier(regularizer), BN 등을 포함한 개선 결과로 제시된다. Lucid 구현은 그중 아키텍처 골격과 핵심 모듈 구성을 코드로 제공하며, 학습 레시피(RMSProp, label smoothing 등)는 모델 코드 바깥(optimizer/손실)에서 구현되는 것이 일반적이므로 본 파일에는 포함되지 않는다.

1️⃣ 베이스 클래스: `Inception`

Lucid에서 Inception 계열은 공통적으로 Inception(nn.Module)을 베이스로 두고, num_classes와 use_aux 같은 설정을 저장한다. forward는 타입만 열어두고(튜플 반환), 실제 계산은 하위 클래스가 구현한다.

class Inception(nn.Module):
    def __init__(self, num_classes: int, use_aux: bool | None = True) -> None:
        super().__init__()
        self.num_classes = num_classes
        self.use_aux = use_aux

    @override
    def forward(self, x: Tensor) -> Tuple[Tensor | None, ...]:
        return super().forward(x)

이렇게 베이스를 분리해두면, 하위 클래스들이 공통 파라미터를 공유하면서도 forward 반환 형태(보조 헤드 포함 여부)를 유연하게 바꿀 수 있다.

2️⃣ 보조 분류기: `_InceptionAux`

논문은 auxiliary classifier를 최적화 가속이 아니라 regularizer 관점에서 재해석한다. 그리고 side head에 BN이나 dropout을 주면 성능이 좋아졌다고 말한다.

Lucid의 _InceptionAux는 그 구조를 다음처럼 구현한다.

AdaptiveAvgPool2d(pool_size)로 공간 크기를 고정
1×1 conv로 채널을 128로 만들고
FC 1024 + ReLU + dropout(p=0.7)
FC로 클래스 로짓 출력

class _InceptionAux(nn.Module):
    def __init__(
        self, in_channels: int, num_classes: int, pool_size: tuple[int, int]
    ) -> None:
        super().__init__()

        self.avgpool = nn.AdaptiveAvgPool2d(pool_size)
        self.conv = nn.ConvBNReLU2d(in_channels, 128, kernel_size=1)

        self.fc1 = nn.Linear(128 * pool_size[0] * pool_size[1], 1024)
        self.fc2 = nn.Linear(1024, num_classes)

        self.relu = nn.ReLU()
        self.dropout = nn.Dropout(p=0.7)

    def forward(self, x: Tensor) -> Tensor:
        x = self.avgpool(x)
        x = self.conv(x)

        x = x.reshape(x.shape[0], -1)
        x = self.fc1(x)
        x = self.dropout(self.relu(x))
        x = self.fc2(x)

        return x

논문은 5×5 stride 3 average pooling로 4×4를 만든다고 설명하지만, Lucid는 adaptive pooling으로 목표 출력 크기 자체를 고정한다. 목적은 동일하고 구현이 더 일반화된 형태다.

3️⃣ 35×35 Inception 모듈: `_InceptionModule_V2A`

논문은 5×5를 3×3 두 번으로 대체하는 factorization을 설명하며, 그 구조를 Inception 모듈에 반영한 형태를 제시한다.

Lucid의 _InceptionModule_V2A는 35×35 스테이지에 해당하는 Inception 블록으로, branch1에서 3×3을 두 번 쌓는 경로가 핵심이다.

class _InceptionModule_V2A(nn.Module):
    def __init__(self, in_channels: int) -> None:
        super().__init__()

        self.branch1 = nn.Sequential(
            nn.ConvBNReLU2d(in_channels, 64, kernel_size=1),
            nn.ConvBNReLU2d(64, 96, kernel_size=3, padding=1),
            nn.ConvBNReLU2d(96, 96, kernel_size=3, padding=1),
        )

        self.branch2 = nn.Sequential(
            nn.ConvBNReLU2d(in_channels, 48, kernel_size=1),
            nn.ConvBNReLU2d(48, 64, kernel_size=3, padding=1),
        )

        self.branch3 = nn.Sequential(
            nn.MaxPool2d(kernel_size=3, stride=1, padding=1),
            nn.ConvBNReLU2d(in_channels, 64, kernel_size=1),
        )

        self.branch4 = nn.ConvBNReLU2d(in_channels, 64, kernel_size=1)

    def forward(self, x: Tensor) -> Tensor:
        return lucid.concatenate(
            [self.branch1(x), self.branch2(x), self.branch3(x), self.branch4(x)],
            axis=1,
        )

여기서도 Inception 스타일의 핵심인 병렬 경로 + 채널 concat이 그대로 유지되며, 큰 커널 경로는 작은 커널 스택으로 대체된다.

4️⃣ 35×35 → 17×17 Grid Reduction: `_InceptionReduce_V2A`

논문은 grid reduction에서 병목이 생기지 않도록, stride 2 downsampling을 병렬 경로로 구성해 concat하는 블록을 제시한다.

Lucid의 _InceptionReduce_V2A는 3개 경로를 병렬로 두고 17×17로 내려간다.

class _InceptionReduce_V2A(nn.Module):
    def __init__(self, in_channels: int) -> None:
        super().__init__()

        self.branch1 = nn.Sequential(
            nn.ConvBNReLU2d(in_channels, 64, kernel_size=1),
            nn.ConvBNReLU2d(64, 96, kernel_size=3, padding=1),
            nn.ConvBNReLU2d(96, 96, kernel_size=3, stride=2),
        )

        self.branch2 = nn.ConvBNReLU2d(in_channels, 384, kernel_size=3, stride=2)
        self.branch3 = nn.MaxPool2d(kernel_size=3, stride=2)

    def forward(self, x: Tensor) -> Tensor:
        return lucid.concatenate(
            [self.branch1(x), self.branch2(x), self.branch3(x)], axis=1
        )

pooling 경로와 conv 경로를 함께 두고 concat하기 때문에, grid가 줄어드는 순간에 표현이 과도하게 줄어드는 병목을 피하려는 설계로 읽을 수 있다.

5️⃣ 17×17 Inception 모듈: `_InceptionModule_V2B`

논문은 n×n을 1×n + n×1로 factorize하는 asymmetric convolution을 제안하고, 17×17 구간에서 1×7과 7×1이 잘 동작했다고 말한다.

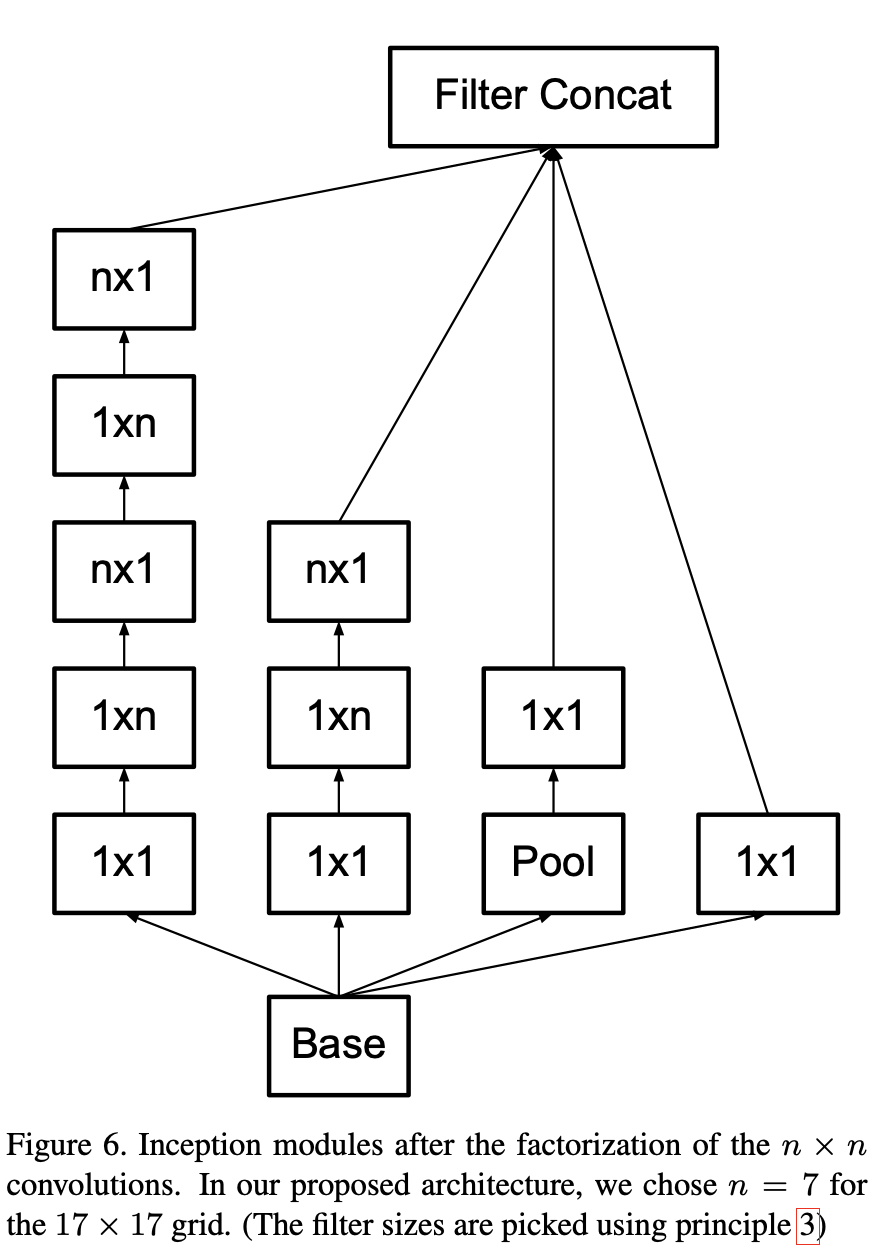
Lucid의 _InceptionModule_V2B는 이 아이디어를 그대로 코드 구조로 드러낸다.

class _InceptionModule_V2B(nn.Module):
    def __init__(self, in_channels: int, out_channels: int) -> None:
        super().__init__()

        self.branch1 = nn.Sequential(
            nn.ConvBNReLU2d(in_channels, out_channels, kernel_size=1),
            nn.ConvBNReLU2d(
                out_channels, out_channels, kernel_size=(1, 7), padding=(0, 3)
            ),
            nn.ConvBNReLU2d(
                out_channels, out_channels, kernel_size=(7, 1), padding=(3, 0)
            ),
            nn.ConvBNReLU2d(
                out_channels, out_channels, kernel_size=(1, 7), padding=(0, 3)
            ),
            nn.ConvBNReLU2d(out_channels, 192, kernel_size=(7, 1), padding=(3, 0)),
        )

        self.branch2 = nn.Sequential(
            nn.ConvBNReLU2d(in_channels, out_channels, kernel_size=1),
            nn.ConvBNReLU2d(
                out_channels, out_channels, kernel_size=(1, 7), padding=(0, 3)
            ),
            nn.ConvBNReLU2d(out_channels, 192, kernel_size=(7, 1), padding=(3, 0)),
        )

        self.branch3 = nn.Sequential(
            nn.MaxPool2d(kernel_size=3, stride=1, padding=1),
            nn.ConvBNReLU2d(in_channels, 192, kernel_size=1),
        )

        self.branch4 = nn.ConvBNReLU2d(in_channels, 192, kernel_size=1)

    def forward(self, x: Tensor) -> Tensor:
        return lucid.concatenate(
            [self.branch1(x), self.branch2(x), self.branch3(x), self.branch4(x)],
            axis=1,
        )

kernel_size=(1, 7)과 kernel_size=(7, 1)의 반복이 곧 논문에서 말한 factorization이며, padding도 (0,3)/(3,0)로 잡아 공간 크기를 유지한다.

6️⃣ 17×17 → 8×8 Grid Reduction: `_InceptionReduce_V2B`

두 번째 grid reduction도 같은 철학으로 병렬 경로를 둔다. 다만 17×17 구간의 1×7/7×1 factorization을 reduction 경로에도 포함한다.

class _InceptionReduce_V2B(nn.Module):
    def __init__(self, in_channels: int) -> None:
        super().__init__()

        self.branch1 = nn.Sequential(
            nn.ConvBNReLU2d(in_channels, 192, kernel_size=1),
            nn.ConvBNReLU2d(192, 192, kernel_size=(1, 7), padding=(0, 3)),
            nn.ConvBNReLU2d(192, 192, kernel_size=(7, 1), padding=(3, 0)),
            nn.ConvBNReLU2d(192, 192, kernel_size=3, stride=2),
        )

        self.branch2 = nn.Sequential(
            nn.ConvBNReLU2d(in_channels, 192, kernel_size=1),
            nn.ConvBNReLU2d(192, 320, kernel_size=3, stride=2),
        )

        self.branch3 = nn.MaxPool2d(kernel_size=3, stride=2)

    def forward(self, x: Tensor) -> Tensor:
        return lucid.concatenate(
            [self.branch1(x), self.branch2(x), self.branch3(x)], axis=1
        )

7️⃣ 8×8 Inception 모듈: `_InceptionModule_V2C`

coarsest grid(8×8)에서는 타일 수가 적기 때문에 채널을 크게 늘려도 계산이 감당 가능하고, 논문 원칙 2의 맥락에서 고차원 표현을 만드는 것이 특히 중요하다고 말한다(Fig. 7). 또한 3×3을 3×1과 1×3으로 쪼개는 asymmetric factorization도 중요한 도구다(Fig. 3).

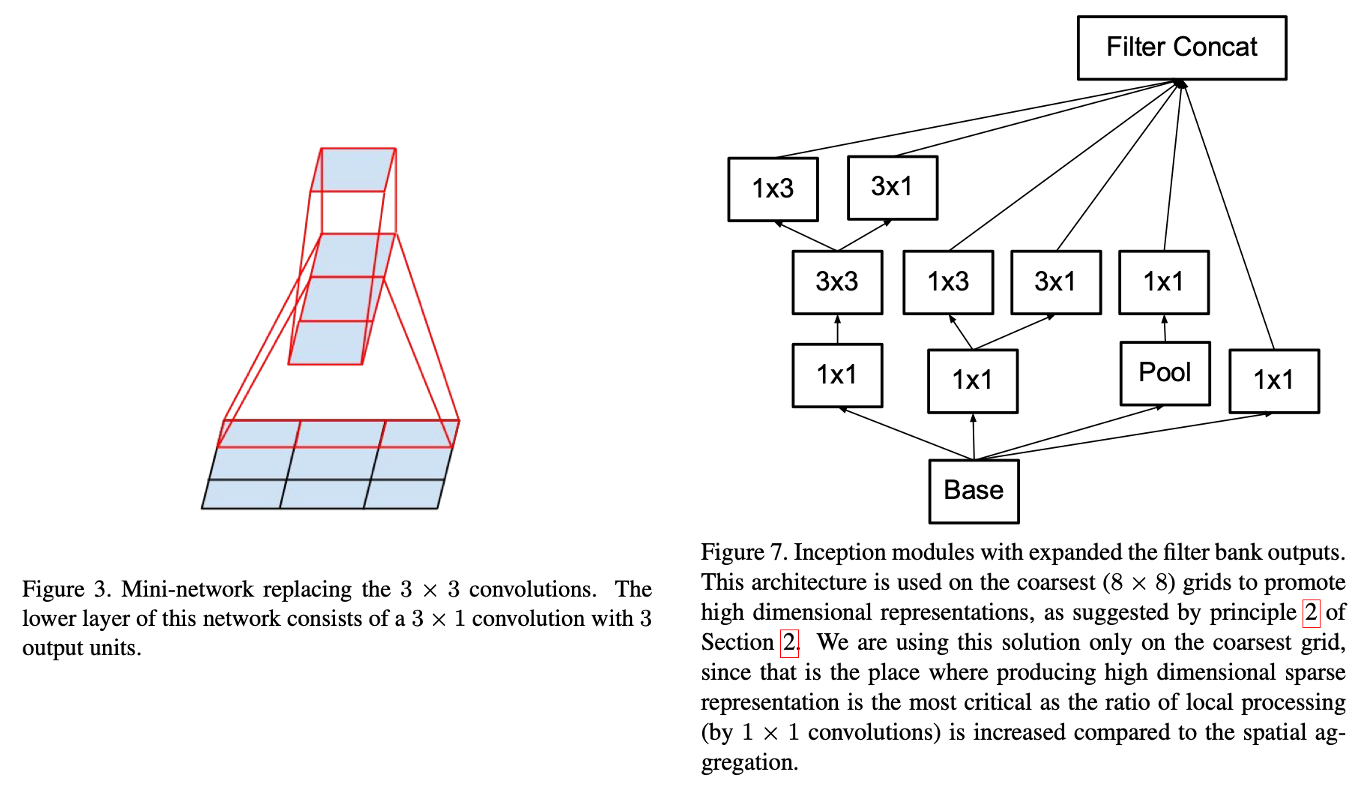
Lucid의 _InceptionModule_V2C는 한 경로에서 3×3을 만든 뒤 이를 (1,3)과 (3,1)로 나눠 concat하는 형태로, 3×3 factorization을 구조적으로 드러낸다.

class _InceptionModule_V2C(nn.Module):
    def __init__(self, in_channels: int) -> None:
        super().__init__()

        self.branch1_stem = nn.Sequential(
            nn.ConvBNReLU2d(in_channels, 448, kernel_size=1),
            nn.ConvBNReLU2d(448, 384, kernel_size=3, padding=1),
        )
        self.branch1_left = nn.ConvBNReLU2d(
            384, 384, kernel_size=(1, 3), padding=(0, 1)
        )
        self.branch1_right = nn.ConvBNReLU2d(
            384, 384, kernel_size=(3, 1), padding=(1, 0)
        )

        self.branch2_stem = nn.ConvBNReLU2d(in_channels, 384, kernel_size=1)
        self.branch2_left = nn.ConvBNReLU2d(
            384, 384, kernel_size=(1, 3), padding=(0, 1)
        )
        self.branch2_right = nn.ConvBNReLU2d(
            384, 384, kernel_size=(3, 1), padding=(1, 0)
        )

        self.branch3 = nn.Sequential(
            nn.MaxPool2d(kernel_size=3, stride=1, padding=1),
            nn.ConvBNReLU2d(in_channels, 192, kernel_size=1),
        )

        self.branch4 = nn.ConvBNReLU2d(in_channels, 320, kernel_size=1)

    def forward(self, x: Tensor) -> Tensor:
        branch1_stem = self.branch1_stem(x)
        branch2_stem = self.branch2_stem(x)

        branch1 = lucid.concatenate(
            [self.branch1_left(branch1_stem), self.branch1_right(branch1_stem)],
            axis=1,
        )
        branch2 = lucid.concatenate(
            [self.branch2_left(branch2_stem), self.branch2_right(branch2_stem)],
            axis=1,
        )
        branch3 = self.branch3(x)
        branch4 = self.branch4(x)

        return lucid.concatenate([branch1, branch2, branch3, branch4], axis=1)

8️⃣ 전체 네트워크: `Inception_V3`

이제 위 블록들을 실제 순서로 연결한 것이 Inception_V3다. 전체 흐름은 논문 (Table 1)의 스테이지 흐름과 대응된다.

Lucid 구현은 다음과 같다.

class Inception_V3(Inception):
    def __init__(
        self,
        num_classes: int = 1000,
        use_aux: bool = True,
        dropout_prob: float = 0.5,
    ) -> None:
        super().__init__(num_classes, use_aux)
        in_channels = 3

        self.conv1 = nn.Sequential(
            nn.ConvBNReLU2d(in_channels, 32, kernel_size=3, stride=2, conv_bias=False),
            nn.ConvBNReLU2d(32, 32, kernel_size=3, conv_bias=False),
            nn.ConvBNReLU2d(32, 64, kernel_size=3, padding=1, conv_bias=False),
        )
        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2)

        self.conv2 = nn.Sequential(
            nn.ConvBNReLU2d(64, 80, kernel_size=1, conv_bias=False),
            nn.ConvBNReLU2d(80, 192, kernel_size=3, stride=2, conv_bias=False),
            nn.ConvBNReLU2d(192, 288, kernel_size=3, padding=1, conv_bias=False),
        )

        self.incep_3 = nn.Sequential(
            _InceptionModule_V2A(288),
            _InceptionModule_V2A(288),
            _InceptionModule_V2A(288),
        )
        self.incep_red1 = _InceptionReduce_V2A(288)

        self.incep_4 = nn.Sequential(
            _InceptionModule_V2B(768, 128),
            _InceptionModule_V2B(768, 160),
            _InceptionModule_V2B(768, 160),
            _InceptionModule_V2B(768, 160),
            _InceptionModule_V2B(768, 192),
        )
        self.incep_red2 = _InceptionReduce_V2B(768)

        if use_aux:
            self.aux = _InceptionAux(768, num_classes, pool_size=(5, 5))
        else:
            self.aux = None

        self.incep_5 = nn.Sequential(
            _InceptionModule_V2C(1280), _InceptionModule_V2C(2048)
        )
        self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
        self.dropout = nn.Dropout(p=dropout_prob)
        self.fc = nn.Linear(2048, num_classes)

    def forward(self, x: Tensor) -> Tuple[Tensor, Optional[Tensor]]:
        x = self.maxpool(self.conv1(x))
        x = self.conv2(x)

        x = self.incep_3(x)
        x = self.incep_red1(x)
        x = self.incep_4(x)

        if self.aux is not None and self.training:
            aux = self.aux(x)
        else:
            aux = None

        x = self.incep_red2(x)
        x = self.avgpool(self.incep_5(x))

        x = x.reshape(x.shape[0], -1)
        x = self.dropout(x)
        x = self.fc(x)

        return x, aux if self.aux is not None else x

forward의 큰 흐름은

stem에서 해상도를 낮추고
35×35 Inception 블록 3개
reduction으로 17×17
17×17 Inception 블록 5개
reduction으로 8×8
8×8 Inception 블록 2개
global average pooling과 dropout 뒤 linear 분류기

로 읽히며, 논문이 말한 factorization과 grid reduction 설계를 그대로 코드 레벨에서 추적할 수 있다.

또한 보조 분류기는 self.training일 때만 계산되므로, 논문이 말한 inference에서 auxiliary discard와 같은 사용 방식이 된다.

9️⃣ 모델 등록 함수: `inception_v3`

Lucid에서 Inception-v3를 생성하는 entry point는 @register_model이 붙은 팩토리 함수다.

@register_model
def inception_v3(
    num_classes: int = 1000,
    use_aux: bool = True,
    dropout_prob: float = 0.5,
    **kwargs,
) -> Inception:
    return Inception_V3(num_classes, use_aux, dropout_prob, **kwargs)

use_aux는 보조 분류기 사용 여부를, dropout_prob는 마지막 dropout 확률을 조절한다. 논문에서의 label smoothing이나 optimizer 설정은 모델 외부에서 처리되므로, 이 팩토리는 네트워크 구조만 구성한다.

✅ 정리

Inception-v3 논문은 Inception-v1의 방향을 유지하면서, 계산 효율을 무너뜨리지 않는 스케일업을 위해 큰 커널을 작은 커널 조합으로 factorize하고, grid reduction에서의 병목을 병렬 경로 concat으로 해결하며, auxiliary classifier와 label smoothing 같은 regularization을 체계적으로 붙여 성능을 끌어올린다. 특히 5×5를 3×3 두 번으로, 7×7을 1×7과 7×1로, 3×3을 3×1과 1×3으로 분해하는 설계는 단순 절감이 아니라 비선형과 BN을 활용해 표현력을 유지하면서 계산을 줄이는 구조적 아이디어로 제시된다.

Lucid에 구현된 Inception_V3는 이러한 아이디어를 실제 아키텍처로 조직한 형태이며, 35×35 스테이지에서의 3×3 반복, 17×17 스테이지에서의 1×7/7×1 factorization, reduction 블록의 병렬 경로, 그리고 global average pooling 기반 분류기까지 Inception-v3의 핵심 흐름을 코드로 그대로 따라갈 수 있다.

📄 출처

Szegedy, Christian, et al. "Rethinking the Inception Architecture for Computer Vision." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016. arXiv:1512.00567.

안암동컴맹

Korea Univ. Computer Science & Engineering

이전 포스트

[GoogLeNet] Going Deeper with Convolutions

다음 포스트