그래프
그래프
노드와 간선으로 이루어진 자료 구조
(데이터간 관계를 표시하기 위해)
정점(Vertex)들의 집합과 이들을 연결하는 간선(Edge)들의 집합으로 구성된 자료 구조
IVI : 정점의 개수
IEI : 그래프에 포함된 간선의 개수
완전 그래프
정점들에 대해 가능한 모든 간선들을 가진 그래프
부분 그래프
원래 그래프에서 일부의 정점이나 간선을 제외한 그래프
인접(Adjacency)
두 개의 정점에 간선이 존재(연결됨)하면 서로 인접해 있다고 한다.
완전 그래프에 속한 임의의 두 정점들은 모두 인접해있다.
문제에서는 연결보다 인접을 더 많이 씀
ex ) 마을끼리 인접해있다 → 그래프
그래프 경로
경로란 간선들을 순서대로 나열한 것이다.
경로 중 한 정점을 최대한 한번만 지나는 경로를 단순경로라 한다.
시작한 정점에서 끝나는 경로를 사이클이라고 한다.
그래프 표현
간선의 정보를 저장하는 방식, 메모리나 성능을 고려하여 결정
인접 행렬
IVI * IVI 크기의 2차원 배열을 이용해서 간선 정보를 저장
배열의 배열 (포인터 배열)
인접 리스트
각 정점마다 해당 정점으로 나가는 간선의 정보를 저장
간선의 배열
간선(시작 정점, 끝 정점)을 배열에 연속적으로 저장
Union-Find(Disjoint set)
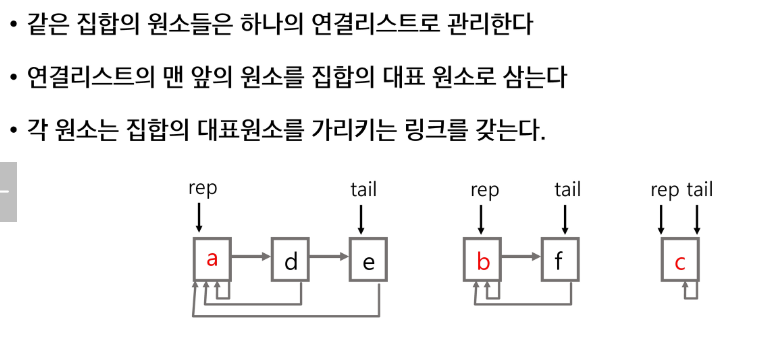
서로소 집합(Disjoint set)
서로소 또는 상호베타 집합들은 서로 중복 포함된 원소가 없는 집합들이다. 다시 말해 교집합이 없다.
집합에 속한 하나의 특정 멤버를 통해 각 집합들을 구분한다 이를 대표자(representative)라 한다.
데이터가 같은 집합에 속해있다 → 관계가 있다.
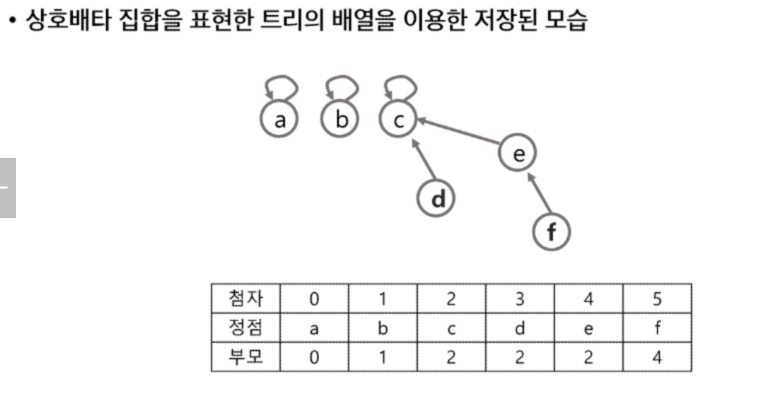
그래프를 나아가 트리로 표현한다.


'''
1~6 까지 노드가 존재
'''
# 1. Make_set
def make_set(n):
return [i for i in range(n)] # 자기 자신이 대표인 데이터 6개가 리스트로 생성됨
# 대표자의 정보를 가지고 있음 (배열에)
# 1~6번까지를 사용하기 위해 7개 생성(0은 버림)
parents = make_set(7)
# 2. find_set : 대표자를 찾아보자
# - 부모 노드를 보고, 부모 노드도 연결이 되어있다면 다시 반복
# - 언제까지? 자기 자신이 대표인 데이터를 찾을때까지
def find_set(x):
# 자기 자신이 대표네? 끝
if parents[x] == x:
return x
# 위의 조건이 걸리지 않았다 == 대표자가 따로 있다.
return find_set(parents[x])
# 3. Union
def union(x, y):
x = find_set(x)
y = find_set(y)
# 이미 같은 집합에 속해있다면 continue
if x == y:
return
# 다른 집합이라면 합침
# 예 ) 더 작은 루트노드에 합쳐라~
if x < y:
parents[y] = x
else:
parents[x] = y
union(1, 3)
union(2, 3)
union(5, 6)