최소 비용 신장 트리 (MST)
그래프에서 최소 비용 문제
-
모든 정점을 연결하는 간선들의 가중치의 합이 최소가 되는 트리
-
두 정점 사이의 최소 비용의 경로 찾기
신장 트리
- n개의 정점으로 이루어진 무방향 그래프에서 n개의 정점과 n-1개의 간선으로 이루어진 트리
최소 신장 트리 (Minimum Spannig Tree)
- 무방향 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치의 합이 최소인 신장 트리
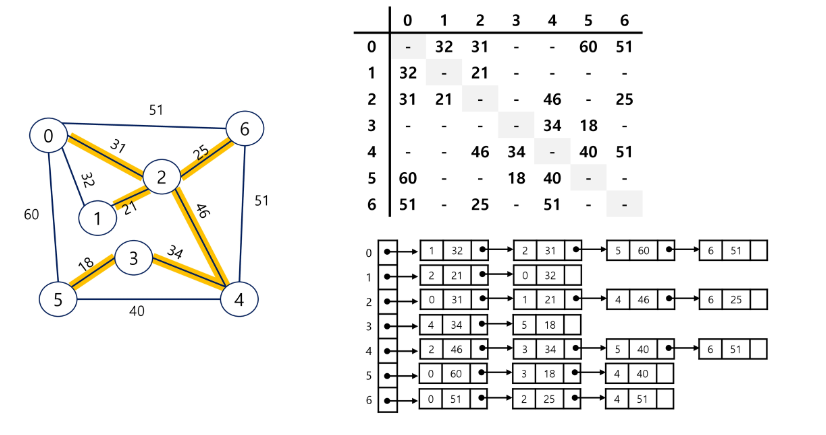
간선의 개수를 최소화하며 모든 정점을 연결하는 방법
-
여러가지 방법이 있다.
-
사이클이 발생하지 않는다.
-
간선의 개수 : (N-1) 개
→ 신장 트리
최소 비용 신장 트리
→ 그 중에서 비용의 합이 가장 작은 트리
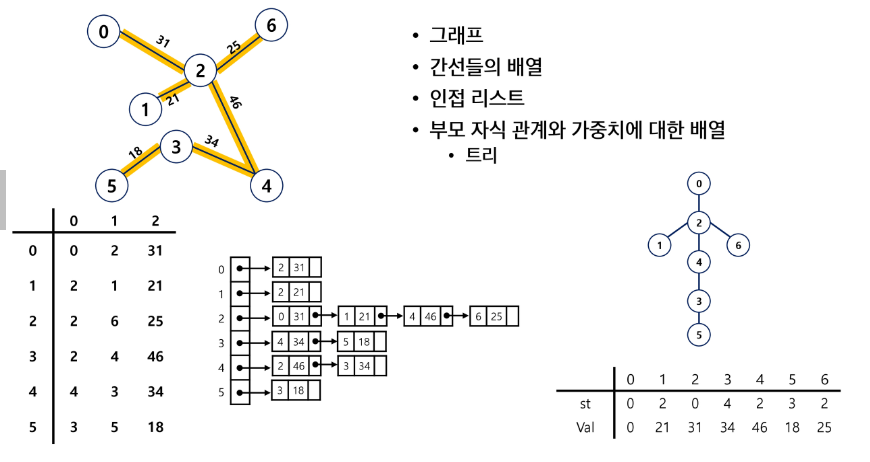
Prim 알고리즘
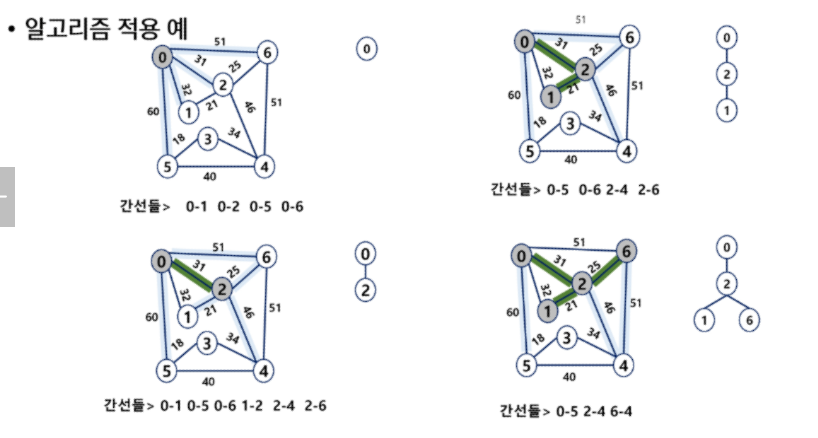
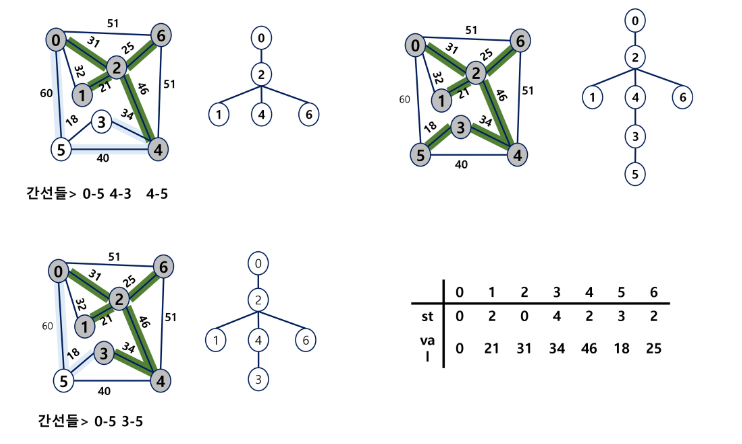
하나의 정점에서 연결된 간선들 중에 하나씩 선택하면서 MST를 만들어 가는 방식
-
임의 정점을 하나 선택해서 시작
-
선택한 정점과 인접한 정점들 중의 최소 비용의 간선이 존재하는 정점을 선택
-
모든 정점이 선택될 때 까지 1, 2 과정을 반복
서로소인 2개의 집합(2 disjoint-set) 정보를 유지
-
트리 정점들 - MST를 만들기 위해 선택된 정점들
-
비트리 정점들(nontree vertices) - 선택되지 않은 정점들
from heapq import heappush, heappop
def prim(start):
pq = []
MST = [0] * V # 방문표시 리스트 (visited와 같은 역할)
# 최소 비용
sum_weight = 0
# 시작점 추가
# [기존 bfs] 노드 번호만 관리
# [PRIM] 우선 순위가 가중치에 따라 정렬 / 가중치가 낮으면 먼저 나와야 한다.
# -> 관리해야 할 데이터는 2가지 : 가중치, 노드번호
# -> 동시에 2가지 데이터 다루는 방법
# 1. class로 만들기
# 2. 튜플로 관리 (오늘 사용할 방법)
heappush(pq, (0, start))
while pq:
weight, now = heappop(pq)
# 우선 순위 큐의 특성 상
# 더 먼 거리로 가는 방법이 큐에 저장되어 있기 때문에
# 기존에 이미 더 짧은 거리로 방문했다면, continue
# 방문했다면 continue
if MST[now]:
continue
# 방문 처리
MST[now] = 1
# 누적합 처리
sum_weight += weight
# 갈 수 있는 노드들을 보면서
for to in range(V):
# 갈 수 없거나 이미 방문했다면 pass
if graph[now][to] == 0 or MST[to] == 1:
continue
# 갈 수 있고 방문하지 않았으면
# pq에 넣기
heappush(pq, (graph[now][to], to))
print(f'최소 비용 : {sum_weight}')
# 정점의 개수 V, 노드의 개수 E
V, E = map(int, input().split())
# 인접 행렬로 저장
# -[과제] 인접 리스트로 저장
graph = [[0] * V for _ in range(V)]
for _ in range(E):
start, end, w = map(int, input().split())
# [기존 의미] : 3에서 4로 갈 수 있다.
# graph[3][4] = 1
# [가중치 그래프] : 3에서 4로 가는데 31이라는 비용이 든다.
# graph[3][4] = 31
# 가중치 저장
graph[start][end] = w
graph[end][start] = w # 무방향 그래프
prim(0)
Kruskal 알고리즘
간선을 하나씩 선택해서 MST를 찾는 알고리즘
-
최초, 모든 간선을 가중치에 따라 오름차순으로 정렬
-
가중치가 가장 낮은 간선부터 선택하면서 트리를 증가시킴
- 사이클이 존재하면 다음으로 가중치가 낮은 간선 선택
- n-1개의 간선이 선택될 때 까지 2를 반복
# 전체 그래프를 보고, 가중치가 제일 작은 간선부터 뽑자
# -> 코드로 구현: 전체 간선 정보를 저장 + 가중치로 정렬
def find_set(x):
if parents[x] == x:
return x
# 경로 압축
parents[x] = find_set(parents[x])
return parents[x]
def union(x, y):
x = find_set(x)
y = find_set(y)
# 같은 집합이면 pass
if x == y:
return
if x < y:
parents[y] = x
else:
parents[x] = y
V, E = map(int, input().split())
edges = [] # 간선 정보들을 모두 저장
for _ in range(E):
s, e, w = map(int, input().split())
edges.append([s, e, w])
edges.sort(key=lambda x:x[2]) # 가중치를 기준으로 정렬렬
parents = [i for i in range(V)] # 대표자 배열
sum_weight = 0
# 간선들을 모두 확인한다.
for s, e, w in edges:
# 싸이클이 발생하면 pass
# 이미 같은 집합에 속해 있다면 pass
if find_set(s) == find_set(e):
continue
# 싸이클이 없으면 방문처리
union(s, e)
sum_weight += w
print(f'최소비용 = {sum_weight}')
# 전체 그래프를 보고, 가중치가 제일 작은 간선부터 뽑자
# -> 코드로 구현: 전체 간선 정보를 저장 + 가중치로 정렬
def find_set(x):
if parents[x] == x:
return x
# 경로 압축
parents[x] = find_set(parents[x])
return parents[x]
def union(x, y):
x = find_set(x)
y = find_set(y)
# 같은 집합이면 pass
if x == y:
return
if x < y:
parents[y] = x
else:
parents[x] = y
V, E = map(int, input().split())
edges = [] # 간선 정보들을 모두 저장
for _ in range(E):
s, e, w = map(int, input().split())
edges.append([s, e, w])
edges.sort(key=lambda x:x[2]) # 가중치를 기준으로 정렬렬
parents = [i for i in range(V)] # 대표자 배열
# MST 완성 = 간선의 개수가 V-1개 일때
cnt = 0
sum_weight = 0
# 간선들을 모두 확인한다.
for s, e, w in edges:
# 싸이클이 발생하면 pass
# 이미 같은 집합에 속해 있다면 pass
if find_set(s) == find_set(e):
continue
print(s, e, w)
cnt += 1
# 싸이클이 없으면 방문처리
union(s, e)
sum_weight += w
if cnt == V: # MST 완성 ! 간선의 개수 == V-1
break
print(f'최소비용 = {sum_weight}')
최단경로 (Dijkstra)
최단 경로 정의
- 간선의 가중치가 있는 그래프에서 두 정점 사이의 경로들 중에서 간선의 가중치 합이 최소인 경로
하나의 시작 정점에서 끝 정점까지의 최단 경로
- 다익스트라 알고리즘
→ 음의 가중치를 허용하지 않음
- 벨만-포드 알고리즘
→ 음의 가중치 허용
모든 정점들에 대한 최단 경로
- 플로이드-워샬 알고리즘
시작 정점에서 거리가 최소인 정점을 선택해 나가면서 최단경로를 구하는 방식이다.
시작 정점(s)에서 끝 정점(t)까지의 최단 경로에 정점 x가 존재한다.
이때 최단 경로는 s에서 x까지의 최단 경로와 x에서 t까지의 최단 경로로 구성된다.
탐욕 기법을 사용한 알고리즘으로 MST의 프림 알고리즘과 유사하다.
