🐹 DP
복잡한 문제를 더 작은 하위 문제로 나누어 해결하는 알고리즘입니다.
동적 계획법에서는 어떤 부분 문제가 다른 문제들을 해결하는데 사용될 수 있어, 답을 여러 번 계산하는 대신 한 번만 계산하고 그 결과를 재활용하는 메모이제이션(Memoization)기법으로 속도를 향상시킬 수 있습니다.
메모이제이션
동일한 계산을 반복해야 할 때, 이전에 계산한 값을 재사용함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술입니다.
2가지 조건
중복되는 부분 문제 - 중복되는 부분 문제는 나눠진 부분 문제가 중복되는 경우로, 메모이제이션 기법을 사용해 중복 계산을 없앱니다.
최적 부분 구조 - 최적 부분 구조를 가진다는 것은 전체 문제의 최적해가 부분 문제의 최적해들로써 구성된다는 것 (즉, 큰 문제를 해결하기 위해 그 문제를 더 작은 부분 문제로 나누었을 때, 각 부분 문제의 최적해를 조합하면 전체 문제의 최적해를 얻을 수 있다는 것입니다)
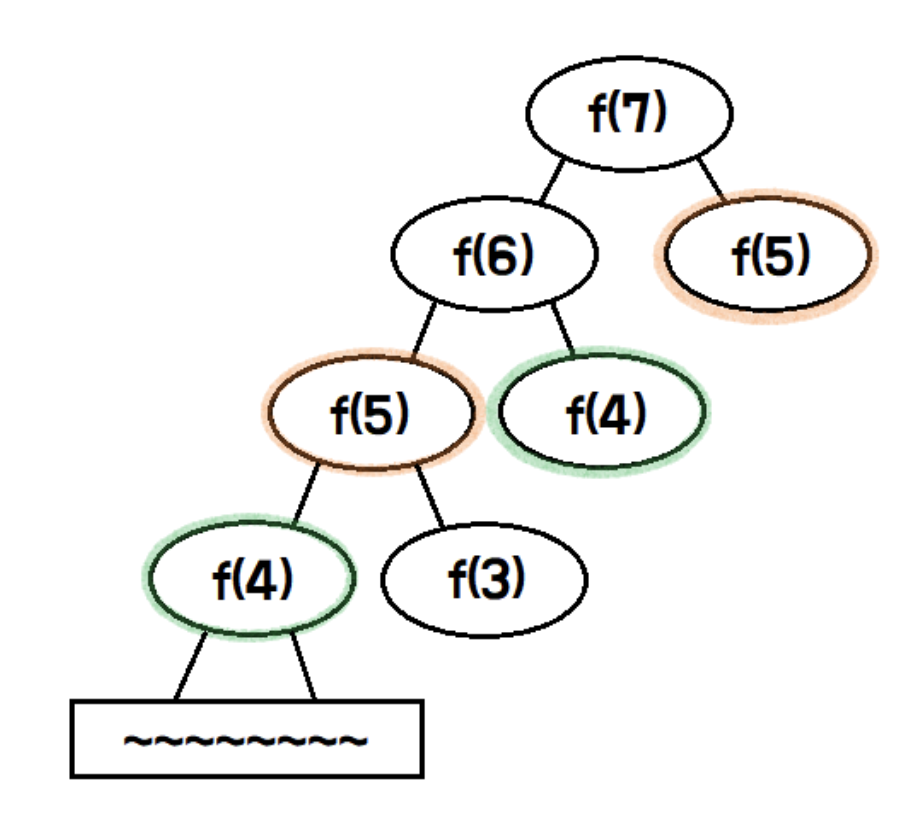
❤️🔥 Top-down 접근 (재귀 사용)
큰 문제를 작은 부분 문제로 나누어 해결하는 방식입니다.
재귀 함수를 사용하여 문제를 작은 부분 문제들로 쪼개고, 중복 계산을 피하기 위해 이전에 계산한 값을 저장하는 메모이제이션을 활용합니다.
public class example {
static int[] dp = new int[8];
public static void main(String[] args) {
System.out.println(fibonacci(7));
}
public static int fibonacci(int n) {
if (n == 0) return 0; // 기저값 설정
if (n == 1) return 1; // 기저값 설정
if(dp[n] > 0 ) return dp[n]; // 캐시 확인
dp[n] = fibonacci(n - 1) + fibonacci(n - 2); // 재귀 호출
return dp[n];
}
}
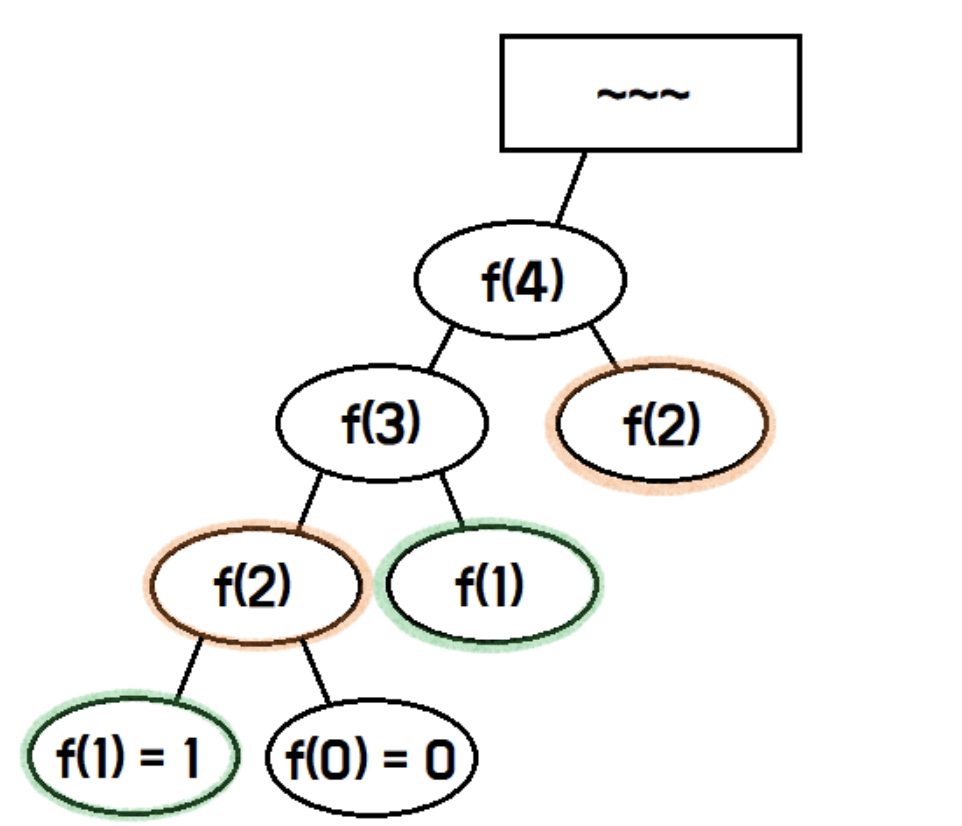
❤️🔥 Bottom-up 접근
작은 부분 문제부터 차례대로 해결하여 전체 문제를 해결하는 방식입니다.
반복문을 사용하여 부분 문제들을 해결하고, 결과를 배열 등에 저장합니다.
public class example {
static int[] dp = new int[8];
public static void main(String[] args) {
System.out.println(fibonacci(7));
}
public static int fibonacci(int n) {
dp[0] = 0; // 기저값 설정
dp[1] = 1; // 기저값 설정
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2]; // 캐시 값으로 다음 값 구하기
}
return dp[n];
}
}
❤️🔥 LIS(최장 증가 부분 수열)
어떤 수열에서 만들 수 있는 부분 수열 중에서 가장 길면서 오름차순을 유지하는 수열을 말합니다.
문제
N개의 자연수로 이루어진 수열이 주어졌을 때, 그 중에서 가장 길게 증가하는 원소들의 집합을 찾는 프로그램을 작성. (작은 수에서 큰 수로)
예를 들어, 원소가 2, 7, 5, 8, 6, 4, 7, 12, 3 이면 가장 길게 증가하도록 원소들을 차례대로 뽑아내면 2, 5, 6, 7, 12를 뽑아내어 길이가 5인 최대 부분 증가수열을 만들 수 있습니다.
public class 최대부분증가수열 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int answer = 0;
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int[] dp = new int[N];
dp[0] = 1;
for (int i = 1; i < N; i++) {
int max = 0; // if 조건이 만족하지 않으면 자기 혼자이므로 dy[i] 갓은 0이 된다. ex) 4, 6, 7, 2
for (int j = i - 1; j >= 0; j--) {
if(arr[j] < arr[i] && dp[j]>max) max = dp[j];
}
dp[i] = max + 1; // 길이가 추가
answer = Math.max(answer, dp[i]);
}
System.out.println(answer);
}
}❤️🔥 냅색 알고리즘 (배낭 문제)
주어진 가방의 용량에 최대한 가치가 높은 물건을 넣는 문제입니다.
각 물건은 가치와 무게를 가지고 있으며, DP를 사용하여 가방의 용량에 따른 최대 가치를 구할 수 있습니다.
배낭 이외데 동전 문제도 냅색 알고리즘에 해당됩니다.
🖇️ 백준 평범한 배낭
🖇️ 동전 문제
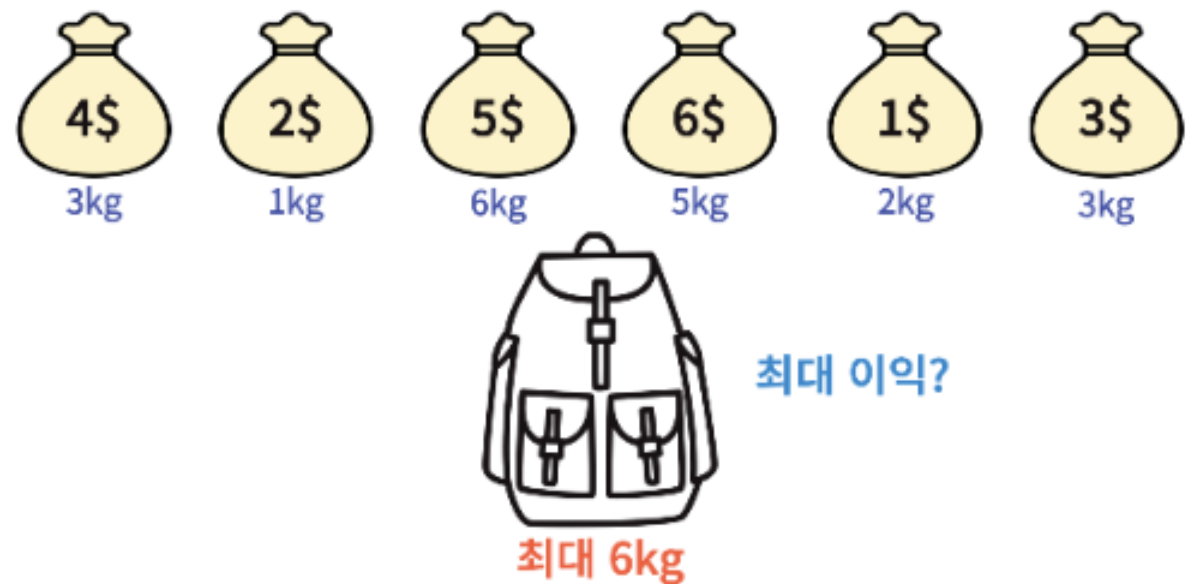
배낭의 최대 용량을 초과하지 않으면서 배낭에 담을 수 있는 최대 가치의 합을 찾는 문제입니다.
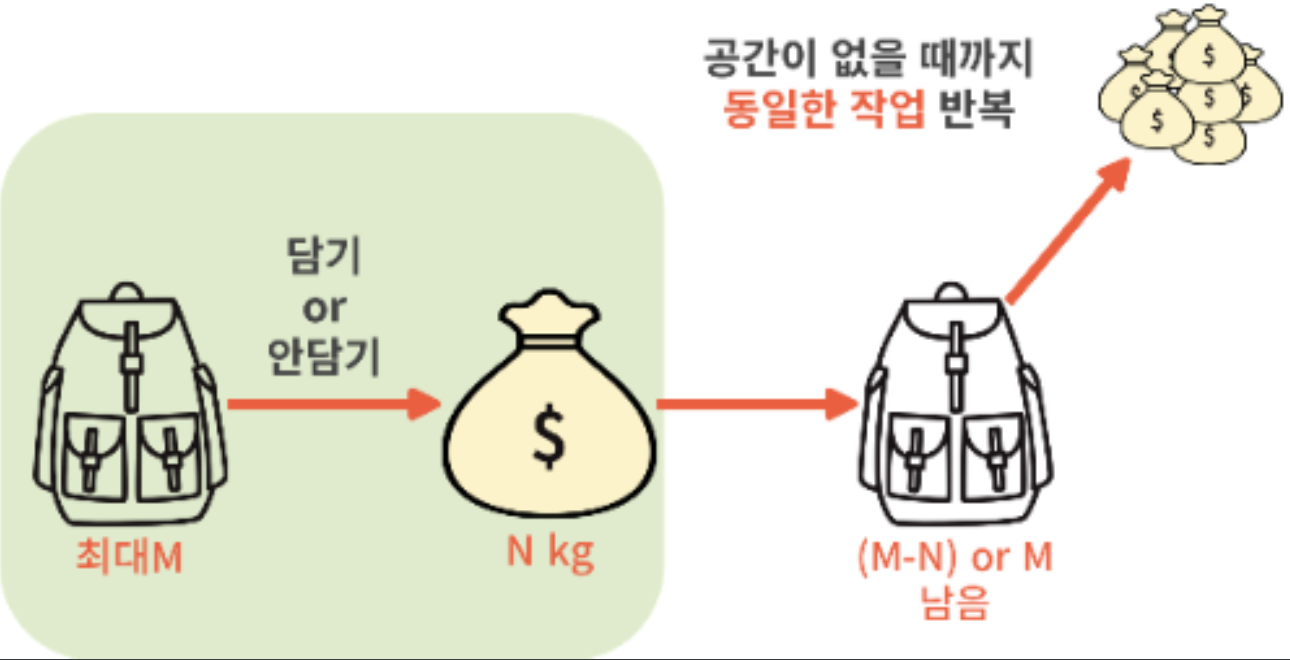
그림에서처럼 배낭에 넣을지 안 넣을지 선택을 하면 되는데 넣는 경우라면 최대 M까지 담을 수 있는 배낭이 있다고 했을 때 배낭에 공간이 (M-N) 으로 남거나 그대로 M이 남거나 입니다.
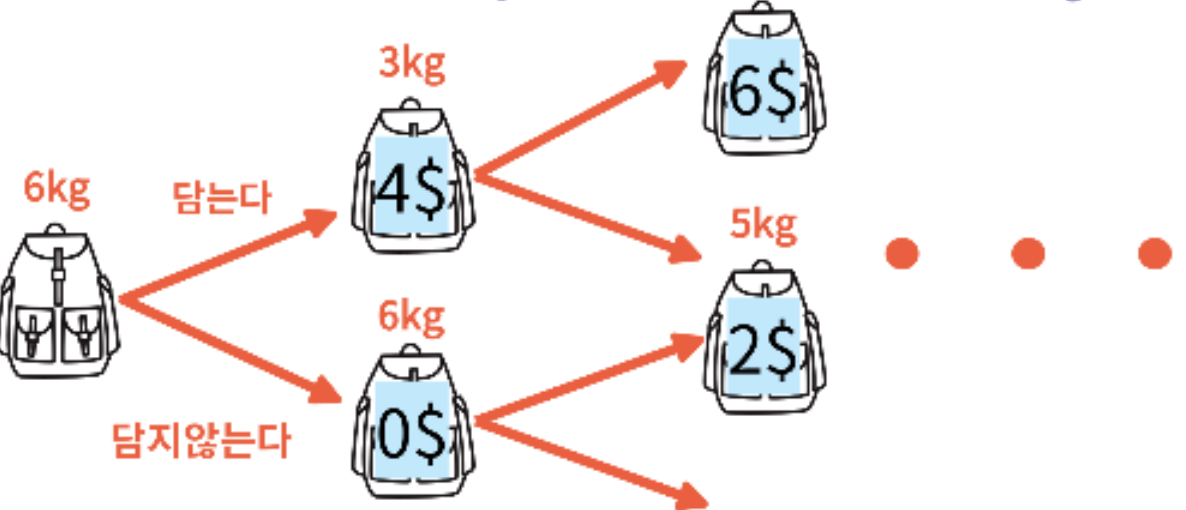
이 과정을 반복해서 최대 가치를 담게 될 경우를 구하면 됩니다.
🖇️ 냅색 알고리즘
❤️🔥 최단 경로 문제
주어진 그래프에서 시작 노드부터 도착 노드까지의 최단 경로를 찾는 문제에 사용합니다.
DP 사용하여 각 노드까지의 최단 거리를 저장하고, 이를 이용하여 최단 경로를 찾을 수 있습니다.
대표적으로 플로이드 와샬이 있습니다.
문제를 보고 싶다면 "이것이 코딩테스트다" 책에서 미래도시를 보면 됩니다.
🖇️ 이것이 코딩테스트다 문제
장단점
중복 계산을 줄일 수 있고 효율적인 시간 복잡도를 가질 수 있습니다. 하지만 메모리 사용량이 큽니다.
DP는 중간 결과를 저장하기 위해 추가적인 메모리를 사용합니다. 따라서 문제의 크기가 커질수록 필요한 메모리도 증가할 수 있습니다.
