2022.06.29 연구실 공부(PyTorch). 'PyTorch로 시작하는 딥 러닝 입문'< 이 글은 이 책의 내용을 요약 정리한 것임.>(내 저작물이 아니고 저 위 링크에 있는 것이 원본임)
05-01 One-hot Encoding & Softmax Regression
Summary
- One-hot Encoding
- Softmax Regression
- MNIST Classification by Softmax Regression
1. One-hot Encoding
- (차원의 개수 = 선택지의 개수) && ((선택지의 index에 해당) ? 1 : 0)
- ex) 강아지, 고양이, 냉장고 라는 3가지 선택지의 경우
강아지 = [1, 0, 0]
고양이 = [0, 1, 0]
냉장고 = [0, 0, 1] - 위와 같은 벡터의 표현 방식을 원-핫 벡터(one-hot vector)라고 함
1-1. 원-핫 벡터의 무작위성
- 적절한 표현 방식임 for 각 클래스 간의 관계가 균등
- 직관적인 방식으로는 정수로 구분을 짓는 정수 인코딩이 더 합리적인 것처럼 보임
- ex) Banana, Tomato, Apple의 경우 {1, 2, 3}으로 정수 인코딩할 경우
Loss function에서 제곱 오차(Squared Error)를 떠올려보자
실제값이 Tomato일때 예측값이 Banana이었다면 제곱 오차 : (2 - 1)^2 = 1
실제값이 Apple일때 예측값이 Banana이었다면 제곱 오차 : (3 - 1)^2 = 4 - 따라서, Banana과 Tomato 사이의 오차보다 Banana과 Apple의 오차가 더 크다! -> 기계에게는 Banana가 Apple보다 Tomato에 더 가깝다는 잘못된 정보를 줄 수 있음.
- Order가 있는 데이터의 경우 : 정수 인코딩이 적합함({baby, child, adolescent, adult}나 {1층, 2층, 3층, 4층}이나 {10대, 20대, 30대, 40대}와 같은 경우)
- 원-핫 벡터의 제곱 오차가 균등함은 아래 식을 통해 확인할 수 있다.
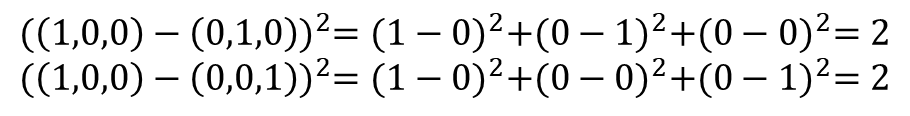
- 원-핫 벡터의 단점 : 단어의 유사성을 표현할 경우 등에는 사용이 어려움.
2. Softmax Regression
2-1. Multi-class Classification
- Multi-class Classification : 세 개이상의 답 중 하나를 고르는 문제를 말함
- 예시) 붓꽃 품종 중 어떤 품종인지를 예측하는 문제(4개의 특성(feature) : 꽃받침 길이, 꽃받침 넓이, 꽃잎 길이, 꽃잎 넓이)
| SepalLengthCm(x1) | SepalWidthCm(x2) | PetalLengthCm(x3) | PetalWidthCm(x4) | Species(y) |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 5.8 | 2.6 | 4.0 | 1.2 | versicolor |
| 6.7 | 3.0 | 5.2 | 2.3 | virginica |
| 5.6 | 2.8 | 4.9 | 2.0 | virginica |
- 입력 : X, 가중치 : W, 편향 : B, 출력 : Y^ -> 각 변수는 Vector/Matrix임.
2-2. Softmax function
- Softmax function : 분류해야하는 정답지(클래스)의 총 개수를 k라고 할 때, k차원의 벡터를 입력받아 각 클래스에 대한 확률을 추정
- k차원 벡터에서 i번째 원소(z_i), i번째 클래스가 정답일 확률(p_i)라 할때, Softmax Function은 p_i를 다음과 같이 정의
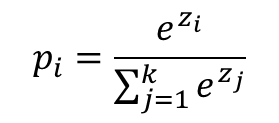
- 따라서, 위에서 말하는 virginica, setosa, versicolor로 구분하는 문제는 곧 virginica일 확률, setosa일 확률, versicolor일 확률로 나타내는 문제이다
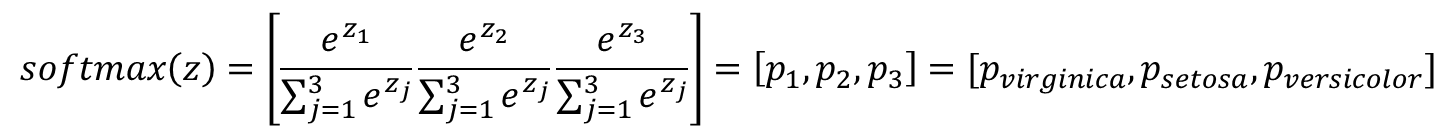
- k차원의 벡터를 입력받아서 모든 벡터 원소의 값을 0과 1사이의 값으로 값을 변경하여 다시 k차원의 벡터를 리턴

- 입력 벡터(z)의 차원 수만큼 결과값이 나오도록 가중치 곱을 진행 -> 화살표는 총 12개(4 * 3 = 12) -> 전부 다른 가중치 -> 학습 중 점점 오차를 최소화하는 가중치로 값이 변경
- 오차 계산 : 클래스의 개수 = 차원의 수인 출력 벡터의 각 원소는 0, 1의 값을 갖는다 -> 예측값과 비교할 수 있는 실제값의 표현방법이 있어야 함 -> 원-핫 벡터 사용
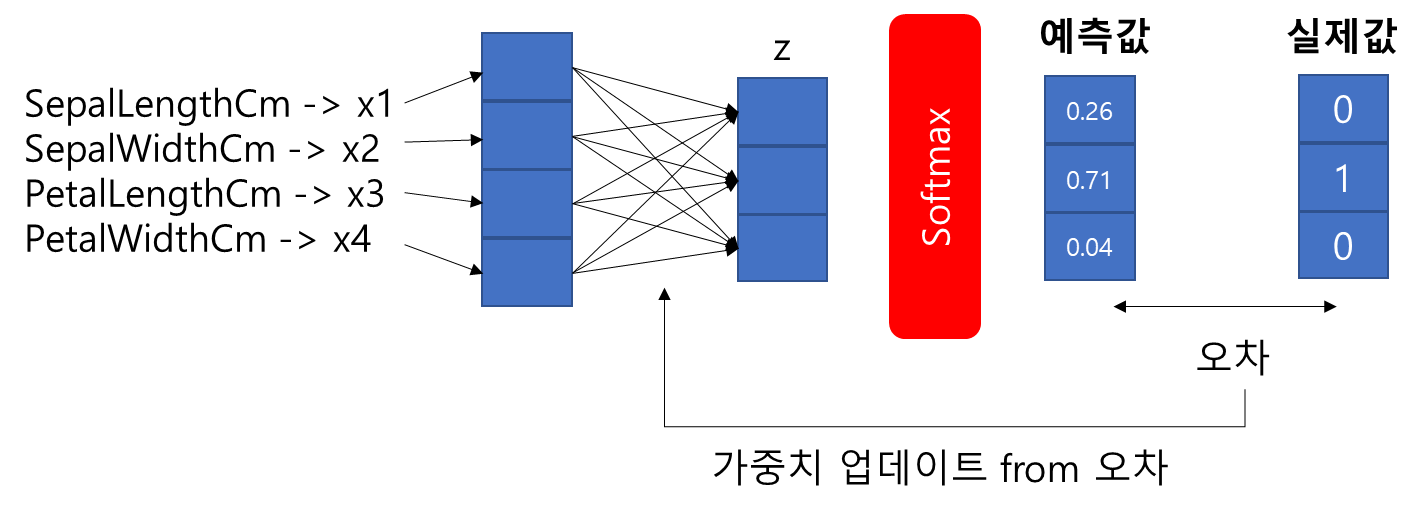
2-3. Softmax function Hypothesis by Matrix
- X : 5 × 4 행렬(입력 데이터)
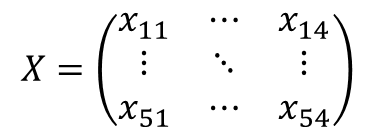
- Y^ : 5 × 3 행렬(예측값)

- W : 4 × 3 행렬(X와 Y^의 크기로 인해)

- B : 5 × 3 행렬(가중치)
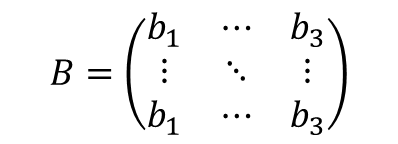
- 가설식
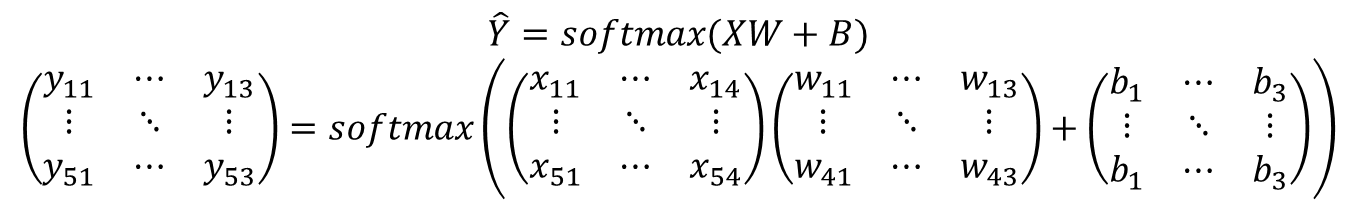
- 위와 같은 가설식으로 나타낼 수 있다.(Matrix 연산 기준)
2-4. Cost function
- 크로스 엔트로피 함수(Cross-entropy function) 사용
- entropy는 예측의 정도에 따라 값이 차이가 나는데, 주로 예측의 정확도에 반비례(예측하기 쉬운 일에서보다, 예측하기 힘든일에서 더 높음)한다.
- 이때, p가 1이면 log(1)=0 이다. -> p가 1이라는 것은 반드시 정확히 예측한 것이고 오차값은 0이 된다. -> 원-핫 인코딩에 적합한 비용 함수이다. -> 이 식의 값을 최소화하는 방향으로 학습 진행
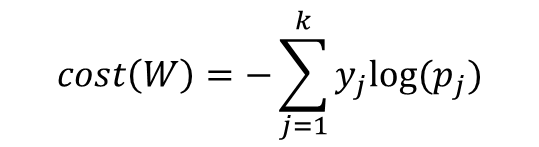
- n개 전체 데이터에 대한 평균을 구한다면 최종 비용 함수는 다음과 같다.
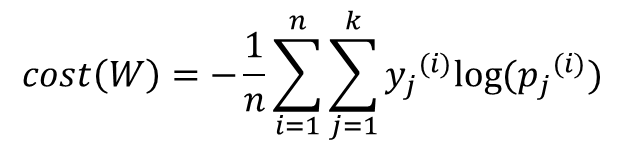
2-5. Cost function of Softmax Regression by PyTorch
Low Level 구현
- 먼저 필요한 도구 임포트 및 랜덤 시드 값을 고정
import torch
import torch.nn.functional as F
torch.manual_seed(1)- 3차원 텐서를 정의하고 Softmax Regression을 이용한 결과값 확인
z = torch.FloatTensor([1, 2, 3])
hypothesis = F.softmax(z, dim=0)
print(hypothesis)tensor([0.0900, 0.2447, 0.6652])- 이제 임의의 3 × 5 행렬의 크기를 가진 텐서 선언 후, dim=1을 통해 2차원에 대한 Softmax 함수를 적용 후 값 확인
z = torch.rand(3, 5, requires_grad=True)
hypothesis = F.softmax(z, dim=1)
print(hypothesis)tensor([[0.2645, 0.1639, 0.1855, 0.2585, 0.1277],
[0.2430, 0.1624, 0.2322, 0.1930, 0.1694],
[0.2226, 0.1986, 0.2326, 0.1594, 0.1868]], grad_fn=<SoftmaxBackward>)- 각 샘플에 대해서 임의의 레이블 부여
y = torch.randint(5, (3,)).long()
print(y)tensor([0, 2, 1])- 모든 원소가 0인 3 × 5 텐서 선언
y_one_hot = torch.zeros_like(hypothesis)
y_one_hot.scatter_(1, y.unsqueeze(1), 1)
print(y_one_hot)tensor([[1., 0., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 1., 0., 0., 0.]])- 교차 엔트로피 함수 구현
cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()
print(cost)tensor(1.4689, grad_fn=<MeanBackward1>)High Level 구현
- torch.log(F.softmax(z, dim=1))은 F.log_softmax()로 구현가능(파이토치에서)
F.log_softmax(z, dim=1)- 교차 엔트로피 구현 관련
(y_one_hot * -torch.log(F.softmax(z, dim=1))).sum(dim=1).mean()(y_one_hot * - F.log_softmax(z, dim=1)).sum(dim=1).mean()F.nll_loss(F.log_softmax(z, dim=1), y)F.cross_entropy(z, y)- 위 4개 식은 전부 같은 코드이며 같은 값을 나타냄
- 단, cross_entropy()는 log_softmax()를 포함한다는 사실을 반드시 기억할 것!
2-6. Softmax Regression by PyTorch
Softmax Regression
- 필요한 도구 임포트 및 랜덤 시드 고정, 훈련 데이터와 레이블 텐서 선언
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)
x_train = [[1, 2, 1, 1],
[2, 1, 3, 2],
[3, 1, 3, 4],
[4, 1, 5, 5],
[1, 7, 5, 5],
[1, 2, 5, 6],
[1, 6, 6, 6],
[1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0]
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)- x_train : 4개의 특성, 8개의 샘플
- y_train : 3개의 클래스(0, 1, 2)
- x_train이 8 × 4, y_train이 8 × 1이므로 원-핫 인코딩한 결과는 8 × 3이어야 함(레이블이 3개이므로)
y_one_hot = torch.zeros(8, 3)
y_one_hot.scatter_(1, y_train.unsqueeze(1), 1)- y_one_hot은 8 × 3이므로 W 행렬은 4 × 3이어야 함
- 옵티마이저는 경사 하강법 이용, 학습률은 0.1
# 모델 초기화
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.1)- F.softmax()와 torch.log()를 사용하여 가설과 비용 함수를 정의하고, 총 1,000번의 에포크를 수행
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# 가설
hypothesis = F.softmax(x_train.matmul(W) + b, dim=1)
# 비용 함수
cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
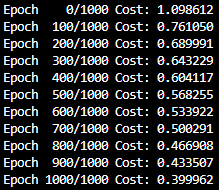
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
- F.cross_entropy()를 사용한 경우
# 모델 초기화
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# Cost 계산
z = x_train.matmul(W) + b
cost = F.cross_entropy(z, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
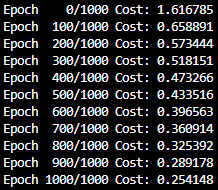
- 같은 결과임을 확인할 수 있음
Softmax Regression by nn.Module
- nn.Linear()를 사용 -> output_dim은 클래스의 개수여야 함(Linear Regression에서는 output_dim이 1이었음)
# 모델을 선언 및 초기화. 4개의 특성을 가지고 3개의 클래스로 분류. input_dim=4, output_dim=3.
model = nn.Linear(4, 3)- 전체 코드
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)
x_train = [[1, 2, 1, 1],
[2, 1, 3, 2],
[3, 1, 3, 4],
[4, 1, 5, 5],
[1, 7, 5, 5],
[1, 2, 5, 6],
[1, 6, 6, 6],
[1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0]
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)
# 모델을 선언 및 초기화. 4개의 특성을 가지고 3개의 클래스로 분류. input_dim=4, output_dim=3.
model = nn.Linear(4, 3)
# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=0.1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.cross_entropy(prediction, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 20번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
Softmax Regression by Class
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)
x_train = [[1, 2, 1, 1],
[2, 1, 3, 2],
[3, 1, 3, 4],
[4, 1, 5, 5],
[1, 7, 5, 5],
[1, 2, 5, 6],
[1, 6, 6, 6],
[1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0]
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)
class SoftmaxClassifierModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(4, 3) # Output이 3!
def forward(self, x):
return self.linear(x)
model = SoftmaxClassifierModel()
# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=0.1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.cross_entropy(prediction, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 20번마다 로그 출력
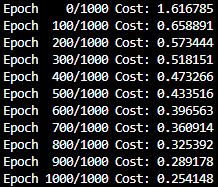
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
3. MNIST Classification by Softmax Regression
3-1. MNIST Dataset
- 숫자 0부터 9까지의 이미지로 구성된 손글씨 데이터셋
- 총 60,000개의 훈련 데이터와 레이블, 총 10,000개의 테스트 데이터와 레이블로 구성 -> 레이블은 0부터 9까지 총 10개
- 각 이미지는 28 픽셀 × 28 픽셀의 이미지임 -> 28 픽셀 × 28 픽셀 = 784 픽셀 -> 총 784의 원소를 가진 벡터로 구성(차원 수가 784)
3-2. 사전 설정
import torch
import torchvision.datasets as dsets
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
import torch.nn as nn
import matplotlib.pyplot as plt
import random
USE_CUDA = torch.cuda.is_available() # GPU를 사용가능하면 True, 아니라면 False를 리턴
device = torch.device("cuda" if USE_CUDA else "cpu") # GPU 사용 가능하면 사용하고 아니면 CPU 사용
print("다음 기기로 학습합니다:", device)- 필요한 도구 임포트(토치비전 필요)
- GPU 연산이 가능하다면 CUDA를 사용하고 그렇지 않으면 CPU연산
- 랜덤 시드 고정
# for reproducibility
random.seed(777)
torch.manual_seed(777)
if device == 'cuda':
torch.cuda.manual_seed_all(777)- 하이퍼파라미터를 변수로
# hyperparameters
training_epochs = 15
batch_size = 100- MNIST Dataset 불러오기
# MNIST dataset
mnist_train = dsets.MNIST(root='MNIST_data/',
train=True,
transform=transforms.ToTensor(),
download=True)
mnist_test = dsets.MNIST(root='MNIST_data/',
train=False,
transform=transforms.ToTensor(),
download=True)- DataLoader로 미니 배치 및 데이터 불러오기 진행
# dataset loader # 배치 크기는 100
data_loader = DataLoader(dataset=mnist_train, batch_size=batch_size,
shuffle=True,
drop_last=True)- 배치 사이즈에 대해 남을 경우 drop_last를 통해 그냥 버릴 수 있음(배치 사이즈가 128인데 나머지가 104개가 남은 경우 drop_last로 버리면 대부분인 128개의 배치들에 비해 상대적으로 104개가 overfitting나는 것을 막을 수 있음)
- 모델을 설계(input_dim = 784, output_dim = 10)
# MNIST data image of shape 28 * 28 = 784
linear = nn.Linear(784, 10, bias=True).to(device)- 비용 함수(교차 엔트로피, 여기서 사용한 torch.nn.CrossEntropyLoss()도 소프트맥스가 포함됨), 옵티마이저(SGD) 정의하기
# 비용 함수와 옵티마이저 정의
criterion = nn.CrossEntropyLoss().to(device) # 내부적으로 소프트맥스 함수를 포함하고 있음.
optimizer = torch.optim.SGD(linear.parameters(), lr=0.1)- 에포크 15로 학습 진행
for epoch in range(training_epochs): # 앞서 training_epochs의 값은 15로 지정함.
avg_cost = 0
total_batch = len(data_loader)
for X, Y in data_loader:
# 배치 크기가 100이므로 아래의 연산에서 X는 (100, 784)의 텐서가 된다.
X = X.view(-1, 28 * 28).to(device)
# 레이블은 원-핫 인코딩이 된 상태가 아니라 0 ~ 9의 정수.
Y = Y.to(device)
optimizer.zero_grad()
hypothesis = linear(X)
cost = criterion(hypothesis, Y)
cost.backward()
optimizer.step()
avg_cost += cost / total_batch
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.9f}'.format(avg_cost))
print('Learning finished')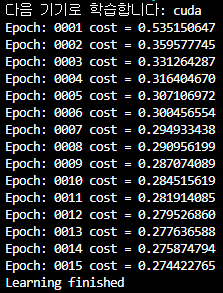
- 테스트 데이터로 모델 테스트
# 테스트 데이터를 사용하여 모델을 테스트한다.
with torch.no_grad(): # torch.no_grad()를 하면 gradient 계산을 수행하지 않는다.
X_test = mnist_test.test_data.view(-1, 28 * 28).float().to(device)
Y_test = mnist_test.test_labels.to(device)
prediction = linear(X_test)
correct_prediction = torch.argmax(prediction, 1) == Y_test
accuracy = correct_prediction.float().mean()
print('Accuracy:', accuracy.item())
# MNIST 테스트 데이터에서 무작위로 하나를 뽑아서 예측을 해본다
r = random.randint(0, len(mnist_test) - 1)
X_single_data = mnist_test.test_data[r:r + 1].view(-1, 28 * 28).float().to(device)
Y_single_data = mnist_test.test_labels[r:r + 1].to(device)
print('Label: ', Y_single_data.item())
single_prediction = linear(X_single_data)
print('Prediction: ', torch.argmax(single_prediction, 1).item())
plt.imshow(mnist_test.test_data[r:r + 1].view(28, 28), cmap='Greys', interpolation='nearest')
plt.show()출처 : 'PyTorch로 시작하는 딥 러닝 입문' <이 책의 내용을 요약 정리한 것임.>
