보통 논문은 Regression보다는 Classification을 사용함.
⇒ 비교/측정하기 좋음.(직관적)
#1. 모델링 방법론
분석방법론
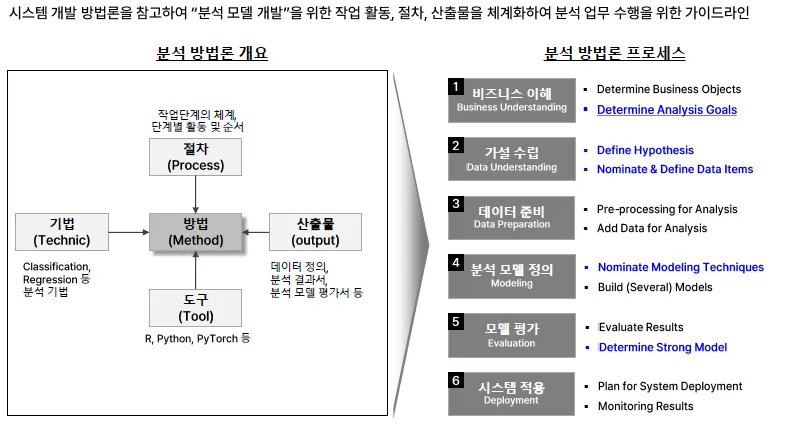
전체 절차
- A. EDA, 탐색적 데이터 분석 (기술통계, 시각화)
- B. 모델 설계 및 학습
- C. 모델 최적화 및 모델 평가
절차별 FAQ
A. 기술 통계 분석
- 평균, 표준편차 등으로 이상치 파악이 가능한지, 실제 업무에 적용할 수 있는지
- 데이터 분포의 왜곡(비대칭성) 여부 확인 방법
- 산점도 등 시각화로 변수 간 상관관계 파악 방법
B. 모델 설계 및 학습
- 문제 해결에 필요한 알고리즘은 어떤 기준으로 선정하는지
- Tree 모델, Boosting 계열 등 다양한 알고리즘 중 선택 기준
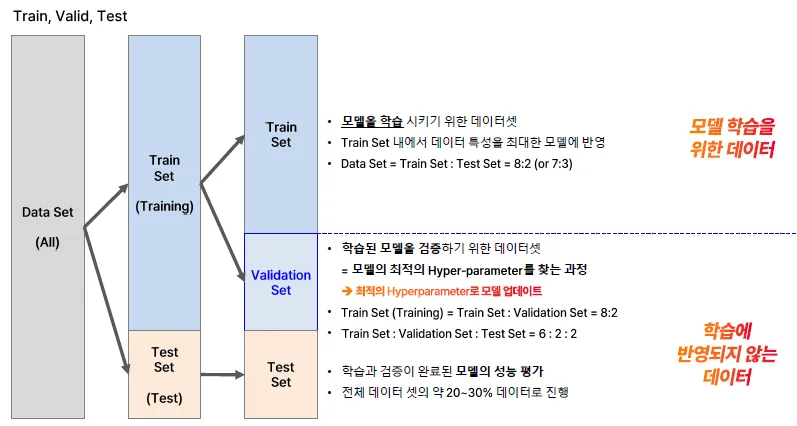
- 데이터셋 분할(Train, Validation, Test)의 목적과 비율 설정 방법
C. 모델 최적화 및 모델 평가
- 1종(Type1) 오류와 2종(Type2) 오류의 차이와 구분 방법
- 과적합(Overfitting) 방지 방법
- 예측 모델의 RMSE 등 성능 평가지표 해석 및 활용 방법
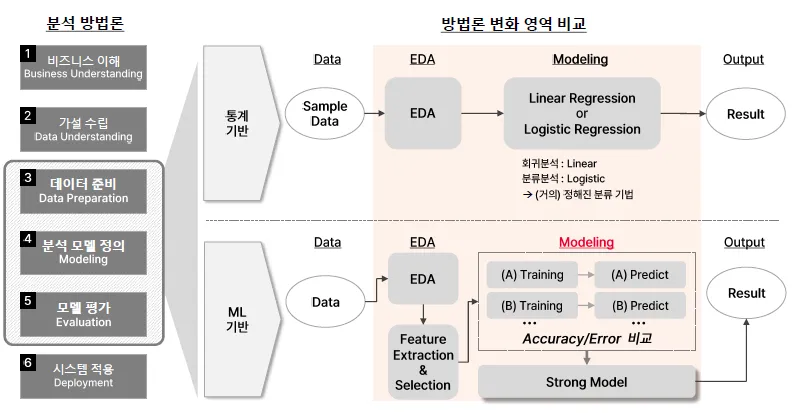
ML 기반에서는 통계 기반에서의 검증 단계를 생략함
최적의 모델을 뽑기 위하여 서로 비교하여 도출함
머신러닝의 종류
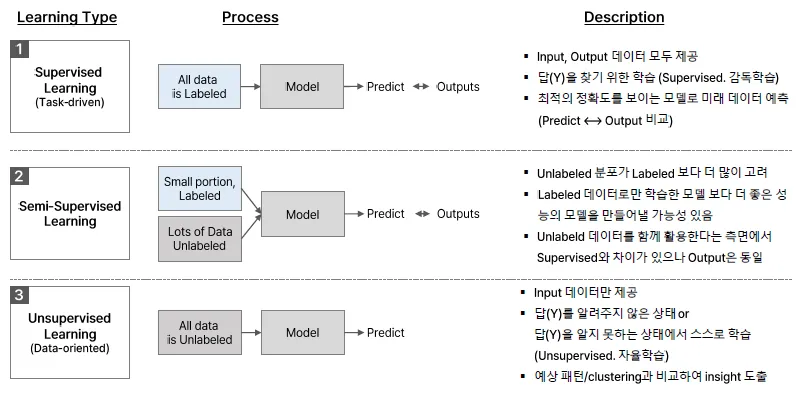
- 그리디 알고리즘
처음부터 최선을 다한다는 느낌으로, 최적의 결과를 찾고자 함
Ex) 의사결정나무
- 엡실론 모델
처음부터 최적의 모델을 찾는 것이 아닌 점차적으로 오류를 줄여나가는 방식으로 학습함.
Ex) 딥러닝
- 사례 기반 모델
실시간으로 가장 가까운 k 개의 Data를 기반으로 결과를 도출함
"비슷한 상황이 과거에 있었는데, 그때 이렇게 해결했어. 그러니까 이번에도 비슷하게 하면 되겠네!”
⇒ 사례(학습 데이터)의 퀄리티가 매우 중요함.
통계 VS 머신러닝
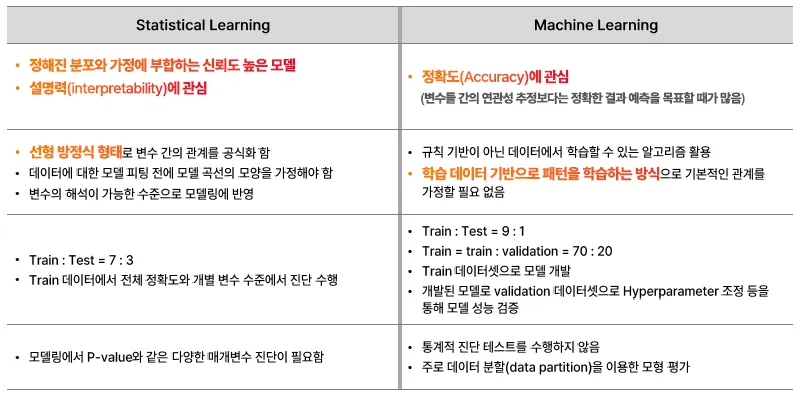
| 구분 | Statistical Learning (통계적 학습) | Machine Learning (머신러닝) |
|---|---|---|
| 관심사 | - 정해진 분포와 가정에 부합하는 신뢰도 높은 모델 - 설명력(해석력)에 관심 | - 정확도(Accuracy)에 관심 - 정확한 결과 예측을 목표로 함 |
| 관계 추정 방식 | - 선형 방정식 형태로 변수 간 관계를 공식화 - 모델 피팅 전 분포/모양 가정 필요 | - 규칙 기반이 아닌 데이터에서 패턴을 학습 - 관계에 대한 가정 불필요 |
| 데이터 분할 | - Train : Test = 7 : 3 | - Train : Test = 9 : 1 - 또는 Train : Validation = 70 : 20 |
| 진단/평가 | - 전체 정확도 및 변수별 수준에서 진단 수행 - p-value 등 통계적 검정 필요 | - 통계적 진단 없이 - 데이터 분할을 통한 모델 평가 |
| 모델링 과정 | - 변수 해석이 가능한 수준으로 모델링 - 다양한 매개변수 진단 필요 | - Train 데이터로 모델 개발 - Validation 데이터로 하이퍼파라미터 조정 등 |
#2. 데이터 분할 전략
Learning VS Inference
학습 데이터를 활용하여 모델을 생성하고, 추론 데이터에 적용하여 Y를 예측
Learning(학습)
- 정의: 분류/예측을 위한 모델(함수)을 생성하는 과정
- 특징:
- 학습 데이터에는 Target(Y) 값이 알려져 있음
- 모델이 과적합되지 않도록 하기 위해 Validation data를 사용
- 학습을 통해 모델이 예측을 잘하도록 최적화됨 (오류 역전파 사용)
Inference(추론)
- 정의: 학습된 모델을 새로운 데이터에 적용하여 예측하는 과정
- 특징:
- 입력 데이터는 학습 때와는 다르며, Target(Y) 값은 알려지지 않음
- 학습된 모델을 그대로 사용해 새로운 입력에 대해 결과를 추론함
Generalization(일반화)
- 정의: 모델이 학습 데이터뿐만 아니라 새로운 데이터에 대해서도 정확하게 예측할 수 있는 능력
- 특징:
- 실제 문제는 훈련 데이터보다 훨씬 다양한 입력이 존재
- 훈련 데이터에만 맞는 모델은 일반화되지 않음 → 오버피팅
- 일반화가 잘 된 모델은 새로운 입력에서도 잘 작동
학습 데이터 내의 특수한 경우까지 학습하여 과적화됨
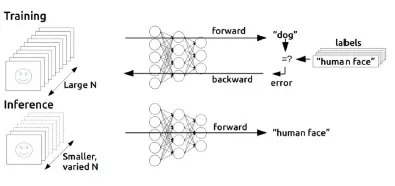
- Training 과정:
- 다수의 라벨이 포함된 데이터를 모델에 입력
- 예측 결과와 실제 라벨의 차이를 바탕으로 모델을 업데이트(오류 역전파)
- Inference 과정:
- 적은 수의 새로운 데이터를 입력하여 예측만 수행 (학습 없음)
Learing Curve
복잡도가 높아질수록 일반화 성능은 감소
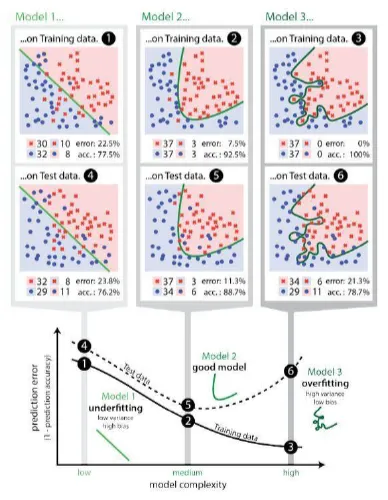
X축 : 모델의 복잡도
Y축 : 예측 오류
모델의 복잡도가 적정선 이상으로 커지면, 모델의 성능이 오히려 떨어짐을 확인
오버피팅
특수한 경우까지 학습하여 일반화 성능이 떨어짐
ML Process
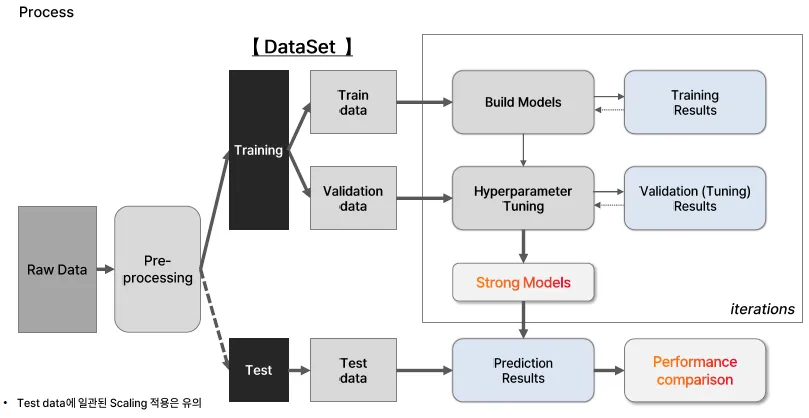
면접 질문: test set이 있는데, validation이 있는 이유
Validation set은 모델을 튜닝하기 위해 필요하고, Test set은 최종 평가용이기 때문에 따로 분리해야 합니다.
Validation set의 역할:
- 모델 훈련 중 하이퍼파라미터 튜닝(예: learning rate, layer 수 등)을 위해 사용
- 과적합 여부를 확인하기 위해 사용
- 훈련 중 모델의 성능을 점검하고 최적의 모델 선택에 활용됨
Test set의 역할:
- 모델 학습 및 튜닝 과정에 절대 사용되지 않음
- 오직 최종 평가에만 사용
- 실제 배포/현업에서 성능이 어떨지를 객관적으로 확인하기 위한 기준
데이터 분할
Cross Validation, 교차검증
학습 데이터셋의 특징을 충분히 반영하여 일관된 성능을 가질 수 있도록 하는 것이 목적임
데이터를 여러 개의 부분(fold)으로 나누어, 모델의 성능을 안정적으로 평가하기 위한 방법
왜 필요한가요?
- Validation set 하나에 의존하면 운 좋게 분할된 데이터로 성능이 과대평가될 수 있음
- 데이터가 적을 때는 train/validation으로 단순 분할하면 정보 손실이 큼
- 모든 데이터를 최대한 활용하면서도 일반화 성능을 평가하고 싶을 때 유용
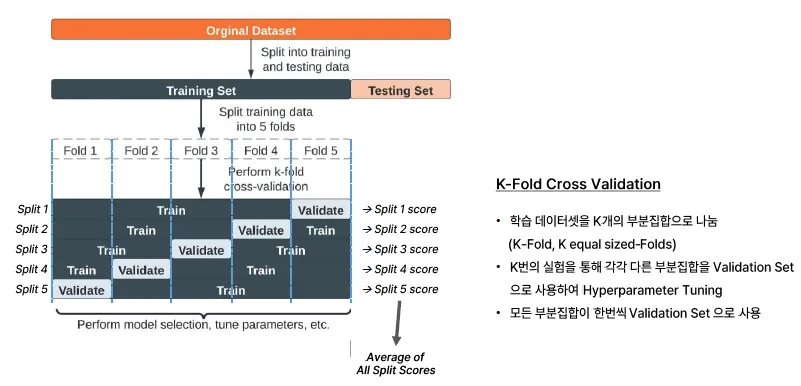
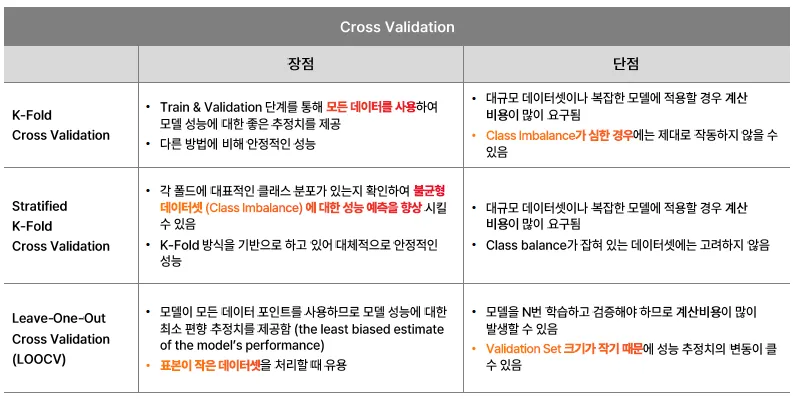
K-Fold Cross Validation
제한된 데이터셋을 활용해 모델의 성능을 정확히 측정하기 위한 연구에서 시작
과정:
- 데이터를 K개의 폴드(fold)로 나눔
- 총 K번 반복:
- 매번 한 폴드를 검증용(validation)으로, 나머지 K-1개를 훈련용(training)으로 사용
- K번의 검증 결과를 평균 내어 최종 성능 평가
- 장점
- 평가 결과가 더 안정적이고 신뢰 가능
- 데이터 효율성이 높음 (모든 데이터가 한 번 이상 validation에 사용됨)
단점
- 모델을 K번 학습해야 하므로 시간이 오래 걸림
- 특히 딥러닝 모델에서는 계산 자원이 많이 소모됨
실전 팁
- Grid Search + Cross Validation을 함께 사용 → 하이퍼파라미터 튜닝 최적화
- Scikit-learn에서는
cross_val_score,KFold등으로 쉽게 구현 가능
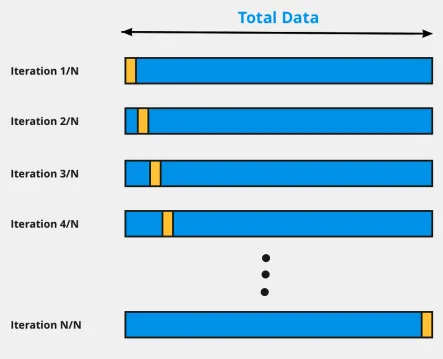
LOOCV, Leave-One-Out- CV
단 하나의 샘플만 Validation set으로 활용
⇒ 데이터셋이 작은 규모인 경우 고려
- n-1개의 샘플을 Train에 활용하므로 bias가 낮음
- Resampling에 따른 임의성이 없음
- 높은 연산 비용
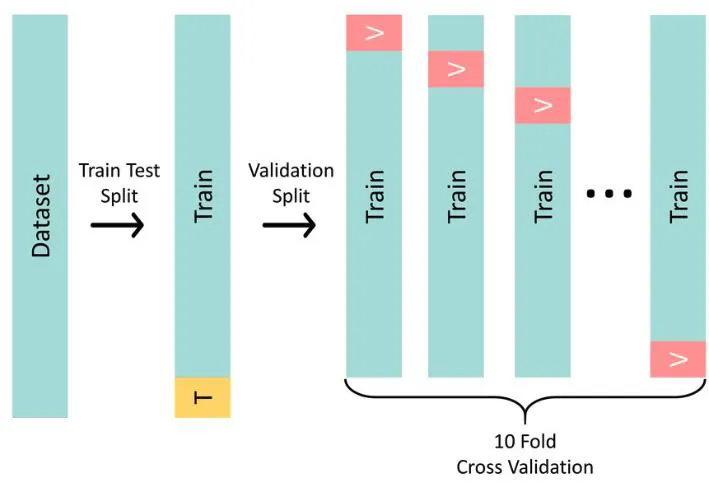
K-Fold CV
k번 학습을 진행하여, k개의 평균
LOOCV보다 낮은 연산비용
- 중간정도의 bias
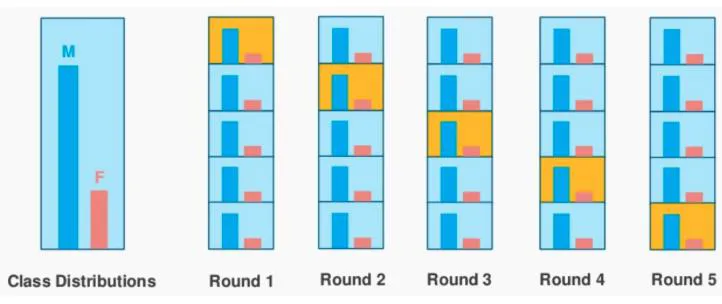
Stratified k-fold CV
계층화된, 분류 문제에 사용
- 비율이 균등하게 유지되도록 분할
생각해보기…

시계열 데이터는 변동이 존재하게 됨. + 최근 패턴을 무시할 수 없음
validation과 test 내의 dynamic이 아까울 수 있음
⇒ 학습을 통해서 구축된 모델에 대해서 배포하기 전에 데이터의 100%를 다시 학습해서 배포함
⇒ 최근의 패턴과 경향도 반영되어서 배포가 됨.
BUT, 선형모델을 사용할 때에는 이러한 방식을 사용하면 안됨.
다시 적합시키면 회귀계수가 다시 Fitting되므로 문제 生
#3. 선형모형 최적화
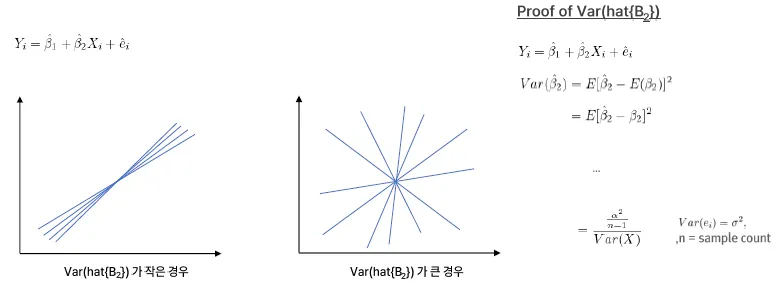
회귀 방정식
- 핵심 개념 요약
- 표본(sample)에 기반한 회귀선 (Regression Line)
- N개의 데이터 샘플을 통해 구한 회귀식
- 여기서 각 β는 표본으로부터 추정한 계수
- 이는 X와 Y의 평균적인 관계를 설명함
- 모집단(Population) 관점의 Y
- 실제 Y값은 예측값에 오차 e_i를 더한 것
- 이 오차는 설명되지 않는 부분 또는 노이즈
- 설명되는 부분 vs. 설명되지 않는 부분
- X에 의해 설명되는 부분: 회귀선
- 설명되지 않는 부분: e_i
- 이 구조는 회귀 분석의 기본 구조
- 모집단 회귀 방정식의 의미
- 우리가 궁극적으로 알고 싶은 것은 모집단의 관계임
- 예: 소득(X)과 소비(Y)의 관계 → 모집단의 특성을 반영
- 모든 사람이 동일한 모델을 따르는 건 아님 (이건 추정된 평균적 관계일 뿐임)
핵심 메시지
- 표본 기반 추정은 모집단의 평균적 관계를 반영하기 위한 방법
- 회귀식은 항상 설명 가능한 부분(선형식) + 설명되지 않는 부분(오차)로 나뉨
- 모델을 해석할 때는 이 불확실성(ei)을 고려해야 신중한 해석이 가능
해당 함수에는 모집단의 특성이 반영되어야 함
회귀방정식의 가정
- 잔차의 평균은 0
- 잔차는 등분산성
- 잔차 간의 공분산 = 0
→ 자기상관이 없다는 말
자기상관(Auto-correlation)이란?
시간이나 순서가 있는 데이터에서, 오차항(Residual)들 사이에 서로 관련성이 있는 현상을 말해.
공식적 정의:
오차항 ei와 e(i+k) 사이의 상관관계(Correlation)가 0이 아닌 경우
→ 자기상관이 존재한다고 해.
만약 오늘의 주식 가격 변화가 어제의 변화랑 비슷한 방향이라면?
- 오늘 주가가 오르면, 내일도 오를 확률이 큼
- → 이건 서로 독립적이지 않음
- → 시간적으로 연관이 있음 = 자기상관이 존재
- 자기상관이 왜 문제인가?
회귀 분석에서는 오차항들이 서로 독립적이라고 가정함 (Assumption 3)
하지만 자기상관이 생기면 이 가정이 깨짐 → 문제 발생:
문제점
- *표준 오차(standard error)가 과소 추정됨 → t-검정, F-검정 왜곡**
- 신뢰구간, p-value 부정확 → 잘못된 의사결정
- 모델의 예측력 저하
언제 자주 나타나나?
- 시계열 데이터 (시간 순서): 주가, 날씨, 트래픽 등
- 예: "오늘 날씨가 더우면 내일도 더울 확률이 높다" → 자기상관 있음
진단 방법:
- 잔차 플롯(residual plot): 시간에 따라 패턴이 보이면 의심
- Durbin-Watson 통계량: 2에 가까우면 자기상관 없음
- 0~2: 양의 자기상관
- 2~4: 음의 자기상관
해결 방법:
- AR, ARIMA 등 시계열 모델 사용
- Newey-West 표준 오차로 보정
- GLS(Generalized Least Squares) 같은 방법 사용
요약
| 항목 | 내용 |
|---|---|
| 정의 | 오차들이 시간적으로 서로 연관 있는 현상 |
| 문제점 | 회귀 가정 위배 → 검정, 예측 신뢰도 하락 |
| 진단 방법 | 잔차 플롯, Durbin-Watson 통계량 |
| 해결 방법 | 시계열 모델, 보정된 표준 오차 사용 |
불편추정량
- 불편성
불편성이란, 어떤 모수의 추정량의 기댓값이 원래 모수가 되는 성질
표본 분산에 대해 평균을 내면 모집단의 분산이 되는데, 이를 불편 추정량이라고 함. 말 그대로 편의가 없는, 치우침이 없는 정확한 추정량이라는 것
표본을 이용해 모수(모집단의 특성)를 추정할 때, 그 추정값의 평균이 실제 모수와 같다면
→ 그 추정량은 불편(Unbiased) 이라 함.
불편성과 다른 개념들
| 개념 | 의미 |
|---|---|
| 불편성(Unbiasedness) | 평균적으로 정답에 가까움 |
| 일치성(Consistency) | 표본이 커질수록 진짜 값에 가까워짐 |
| 효율성(Efficiency) | 불편추정량들 중 분산이 가장 작음 |
요약 정리
| 용어 | 의미 |
|---|---|
| 불편추정량 | 평균적으로 정답을 정확히 추정 |
| 주의 | 불편하지만 분산이 클 수도 있음 (항상 최적 아님) |
강건성(Robustness)
모형의 복잡도와 강건성
왼쪽 텍스트 요약: "견고성(Robustness)이란?"
- 강건성(Robustness)이란, 모델이 다음과 같은 경우에도 예측 성능을 안정적으로 유지하는 능력
- 예상치 못한 상황이나 환경 변화 (ex. 데이터의 분포가 바뀜)
- 노이즈나 입력값의 변동
- 데이터 품질 저하 또는 드물게 발생하는 특이한 상황
즉, 현실 세계에서 모델을 실제로 사용할 때의 신뢰도를 높이는 핵심 요소야.
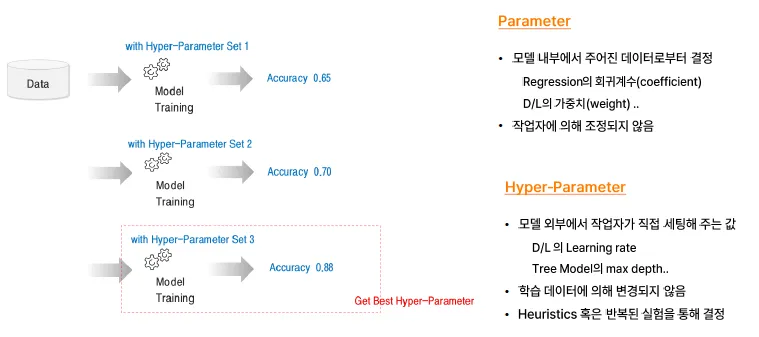
색깔별 그래프 설명
- 🟢 Training Sample (녹색): 복잡도가 높을수록 학습 데이터에 대해 정확도↑
- 🔵 Test Sample (파란색): 일반화된 정확도는 적절한 복잡도에서 최고 → 너무 단순하면 Underfitting, 너무 복잡하면 Overfitting
- 🔴 Shifted/Modified Test Sample (빨간색): 환경이 바뀌거나 예기치 않은 상황에서 성능이 떨어짐 → 여기서 견고성(Robustness) 이 중요하게 작용!
- Underfitting (High Bias, Low Variance): 모델이 너무 단순해서 데이터를 잘 설명하지 못함
- Overfitting (Low Bias, High Variance): 너무 복잡해서 훈련 데이터에 과적합됨 → 적절한 타협이 필요 (Bias-Variance Trade-off)
핵심 포인트 요약
| 항목 | 설명 |
|---|---|
| 견고한 모델 | 현실 변화에도 성능이 크게 떨어지지 않음 |
| 모델 복잡도 | 너무 낮으면 underfitting, 너무 높으면 overfitting |
| Robustness vs Accuracy | Accuracy만 추구하면 변화에 약해질 수 있음 |
| 현실 적용 | 예측 모델이 신뢰도 있게 동작하려면 견고성이 필요 |
본 사례에서 모형개발 최적화 방안을 작성해보세요.
(1)이상치는 중요한 정보일 수 있어 되도록이면 제거없이 모델링에 활용하고싶다
(2)재무비율마다 상이한 스케일 문제를 해소하고싶다
(3)변수들의 비교 가능성을 확보할 수 있는 일관된 설명력을 얻고싶다
(4)일반화를 통해 모델의 강건성을 확보하고 싶다
모형개발 최적화 방안
(1) 이상치는 중요한 정보일 수 있어 제거 없이 활용하고 싶다
- Robust Scaler 사용 : 이상치의 영향을 줄이면서 데이터 분포의 중심(중앙값)과 범위(IQR 기준)를 기준으로 스케일링 → 평균과 표준편차 대신, 중앙값(median)과 사분위 범위(IQR)를 사용 → 이상치를 제거하지 않고도 모델의 안정성 확보 가능
"이상치를 배제하지 않되, 전체 스케일 계산에 지나치게 영향을 주지 않게 하자”
- 트리 기반 모델 활용 : Random Forest, XGBoost 같은 트리 모델은 이상치에 상대적으로 덜 민감 → 선형 회귀보다 이상치의 영향이 적음
(2) 재무비율마다 상이한 스케일 문제 해결
- 스케일 조정 (정규화 또는 표준화)
StandardScaler(평균 0, 표준편차 1)RobustScaler(중앙값 기준)MinMaxScaler(0~1 스케일) 선택 기준:
- 이상치가 많다면 → RobustScaler
- 모델이 거리 기반(KNN, SVM 등)이라면 → MinMaxScaler
- 일반적인 선형 모델이라면 → StandardScaler
(3) 변수들의 비교 가능성을 확보하고 싶다
- 표준화(Standardization)를 적용하여 모든 변수들을 동일한 스케일로 맞춰 → 회귀 계수나 피처 중요도 해석 시, 서로 비교 가능 → 특히 선형 회귀에서 해석력을 높이기 위해 필수적인 전처리
- 공헌도(Feature Importance) 기반 해석 : 모델 학습 후, 변수의 중요도를 시각화하여 비교 → 모델 해석성 확보
(4) 일반화를 통해 모델의 강건성 확보
- K-Fold Cross Validation : 과적합 방지 및 모델의 일반화 성능 확인 → 다양한 데이터 셋 분할을 통해 일관된 성능 평가
- Regularization 적용 : L1(Lasso), L2(Ridge) 규제 추가 → 불필요한 변수의 영향 줄이고, 일반화 성능 향상
- Feature Selection/Engineering : 불필요한 변수 제거 + 파생변수 생성으로 모델 단순화 → 해석력 향상 + 성능 개선
- Ensemble 방법 활용 : 여러 모델의 예측을 결합 (Bagging, Boosting 등) → 일반화 성능 및 Robustness 확보
요약 정리
| 요구사항 | 최적화 방안 |
|---|---|
| 이상치 활용 | RobustScaler, 트리 기반 모델 |
| 스케일 문제 | Scaler 사용 (Standard, Robust 등) |
| 변수 비교 가능성 | 표준화 + 변수 중요도 분석 |
| 일반화와 견고성 | 교차검증, 정규화, 앙상블 |
#4. Hyper-parameter Tuning(HPO)
Parameter VS hyperparameter
Parameter (모델 파라미터)
- 학습 데이터로부터 자동으로 학습되는 값
- 예시: 선형회귀(Linear Regression)의 회귀계수(기울기), 절편
- 모델의 구조를 직접 결정하는 값 (→ 모델의 일부)
- 학습 과정에서 업데이트됨
- 모델을 학습시키면 자동으로 얻어짐 → 예:
model.coef_,model.intercept_
Hyper-parameter (하이퍼파라미터)
- 학습 방법이나 알고리즘의 설정을 미리 지정하는 값
- 예시: 결정트리(Decision Tree)의 최대 깊이(max_depth)
- 학습 데이터로부터 학습되지 않음 → 사용자가 직접 설정
- 모델 외부에서 조절하는 값 (→ 모델의 동작 방식 결정)
- 보통 여러 조합을 실험해서 최적값을 찾음 (Grid Search, Random Search 등 사용)
차이 요약
| 항목 | Parameter | Hyper-parameter |
|---|---|---|
| 학습 방법 | 데이터로부터 자동 학습됨 | 사용자가 사전 설정 |
| 위치 | 모델 내부의 값 | 모델 외부 설정값 |
| 예시 | 회귀 계수, 절편 | 트리 깊이, 학습률, batch size 등 |
| 결정 시점 | 학습 중 결정 | 학습 전에 설정 |
| 튜닝 방법 | 최적화 알고리즘에 의해 | 실험(Grid/Random Search 등)으로 |
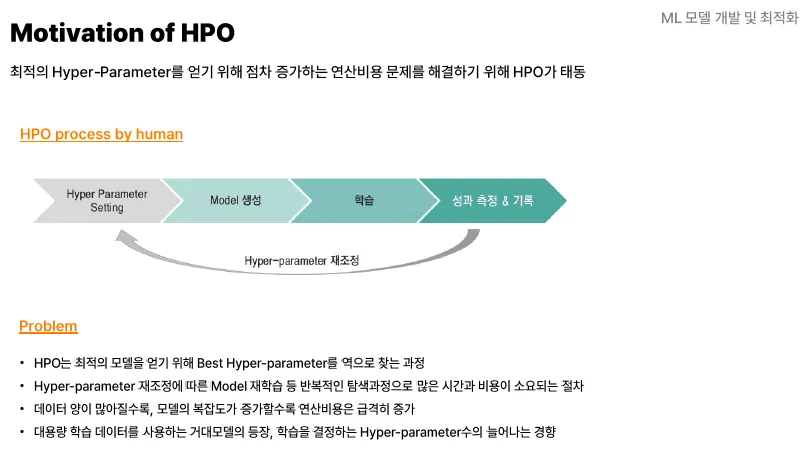
HPO

⇒ 반복적인 탐색을 통해서 최적의 Hyper-parameter를 찾는 과정.
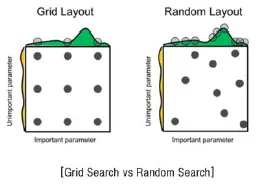
Grid Search
Hyper-parameter의 탐색 범위를 제한한 후 모든 조합을 순차적으로 탐색
- Min/Max 간격을 통해 탐색 범위를 제한
- 탐색할 hyper-parameter 조합들을 Grid에 보관
- Grid의 범위와 하이퍼 파라미터의 수가 늘어날수록 연산량이 기하급수적으로 증가

장점
- 구성이 쉽고 직관적인 방법
- 작업자가 원하는 탐색 범위를 정확하게 비교 분석할 수 있음 ⇒ 작업자가 숙련된 Data Scientist여서 적절한 탐색범위를 제한할 수 있다면 효과적
단점
- 매우 느림
- 균일한 간격으로 탐색하므로 최적해를 지나칠 수 있음
- 모든 구간을 탐색하므로 비효율적
Random Search
Hyper-parameter의 탐색 범위를 제한한 후 설정 횟수만큼 임의의 조합을 탐색
- 균일 간격 탐색이 아니라, Random 탐색을 통해 최적해를 발견할 가능성을 높임
- 탐색할 임의의 조합 수를 직접 설정하기에 불필요한 반복 탐색 감소
단점
- 탐색범위가 넓을 경우 일반화된 결과가 나오지 않음
- 성과가 설정하는 탐색 횟수가 의존적일 수 있음
성능이 가장 높은 최적해로 점차 찾아가는 기법이 아니라,
단순히 탐색 시행을 통해 비교 분석해서 최적해를 찾아가는 기법

Bayesian Search, 베이지안 탐색
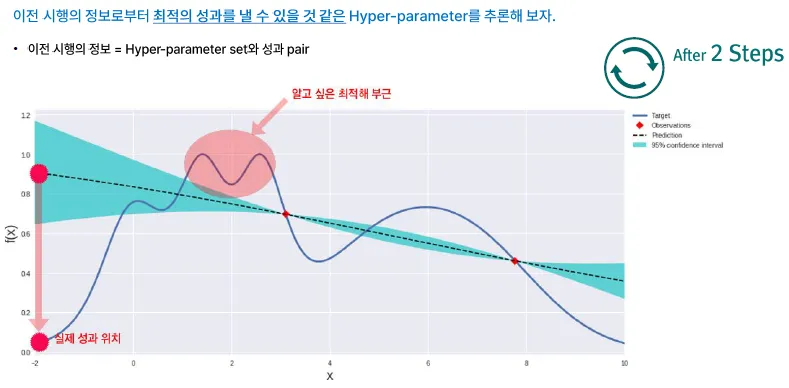
지금 알고 있는 정보(이전의 경험)과 현재의 증거(관측값)로 내가 알고자 하는 값을 점차 추론해(업데이트) 나가는 것
이전 시행의 정보로부터 최적의 성과를 낼 수 있을 것 같은 hyper-parameter를 추론

⇒ 관측치를 가지고 Predict line을 만들어서 실제 곡선(데이터 분포)와 유사하게 맞춰 나가는 방식
장점
- 단순한 Search Method 비해 보다 적은 시도로 최적의 결과를 낼 수 있는 이론적 근거를 가지고 있음. ⇒ 높은 성능의 Hyper-parameter를 찾을 수 있는 가능성 향상
단점
- 최적화 탐색의 속도 문제
- 기존의 탐색결과를 활용하는 Sequential approach 이기에 속도 향상의 한계 & 병렬처리 불가
- 활용(Exploitation)와 탐색(Exploation)의 적절한 Trade-Off
<데이터 분석 방법>
- 처리속도를 향상시킬 수 있는 방법(안될 것 같은 방법은 멈추기)
- 병렬처리에 대한 연구
- 최적의 해를 찾아갈 수 있는 알고리즘 연구
