- 모델 평가
Regression Measurement
실제값과 예측값의 평균적인 차이를 측정하는 것이 목적(오차의 크기)
각 방법론에 장단점이 있기 때문에, 여러 개를 함께 사용하기도 함.
MAE, Mean Absilute Error
데이터와 데이터 평균 간 절대적인 차이의 평균
제곱을 하는 이유는 차이값이 상쇄되는 것을 막기 위하여
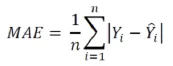
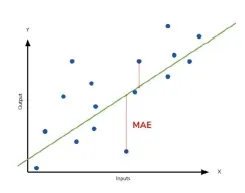
- 데이터의 크기에 의존적(데이터 자체의 크기를 반영하지 못함)
⇒ Scaling해주거나, 데이터 자체의 크기를 고려하도록 해야 함
- 이상치에 상대적으로 덜 민감함
⇒ 이상치에 대한 검정에 분리
MSE, Mean Squared Error
차이 제곱의 평균
제곱을 통해 부호가 상쇄되는 것을 막음
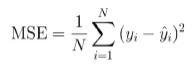
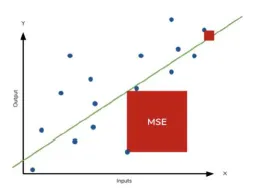
-
실제 데이터와 단위가 다름(제곱)
-
잔차를 제곱하므로 이상치에 민감하게 반응하여 penarty를 줄 수 있음
MAE vs MSE
-
MAE는 오류가 선형적으로 증가, MSE는 지수적으로 증가
-
오류가 1에서 10이 되었다면 MAE는 10배, MSE는 100배 커짐
| 항목 | MAE | MSE |
|---|---|---|
| 계산 방식 | 절댓값 | 제곱 |
| 이상치 민감도 | 낮음 | 높음 |
| 수식의 부드러움 | 비미분 가능점 존재 (절댓값) | 매끄럽게 미분 가능 |
| 해석 용이성 | 직관적 (평균 오차) | 오차의 크기에 민감하게 반응 |
Case Study
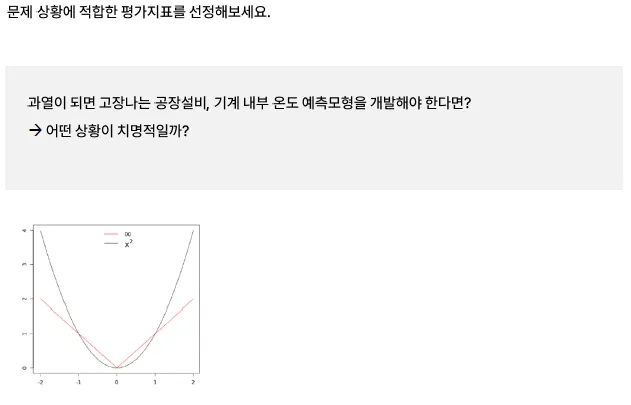
데이터를 통해 미리 조치를 취하고 싶음
- MSE를 사용하는 것이 더 좋음. 큰 오차가 발생하였을 때, 민감하게 반응해야 하므로..
RMSE, Root Mean Squared Error
MSE에 제곱근을 취하여 target과 단위를 동일하게 함으로써 해석성을 확보
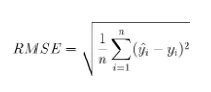
-
Scale에 의존적
-
이상치에 민감하게 반응하는 것은 MSE와 같지만, 그 정도가 덜하다
-
값 자체의 크기가 줄어들어 연산속도가 느려지는 단점을 상쇄함
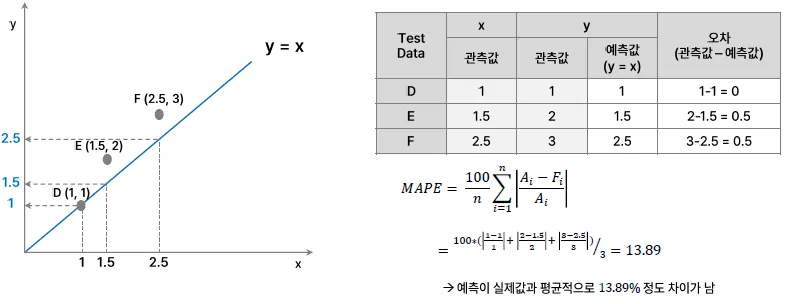
MAPE, Mean Absolute Percentage Error
MAE를 비율로 표현, 지표 자체가 직관적임 (MAE가 5%라면 실제값과 5% 차이)
100을 곱한 이유: 그 자체를 비율로써 표현하기 위함

- Scale에 의존적이지 않으며, 비율로써 표현하였기에 다른 모델 간 비교가 용이함
→ 서로 다른 척도 간의 오차의 크기를 비교 가능
- Actual 값이 0인 경우 계산 불가능

MPE는 잔차 간의 부호가 상쇄되므로 적절하지 않을 수 있음(왜곡 生)
⇒ 그럼에도 방법론이 있는 이유는, 부호가 있으므로 데이터의 방향성을 알 수 있음
+ : Over Estimated
⇒ 수요보다 과도한 경우(재고관리 비용 生)
- : Under Estimated
⇒ 수요가 있음에도 팔지 못하는 경우
MAPE의 단점
-
실제값이 0이면 계산 불가능
-
실제값이 0에 근접한 경우 오류율이 왜곡됨
- 실제값 0.5, 예측값 2 → 300%
- 실제값 0.1, 예측값 2 → 1,900%
WAPE, Weighted APE
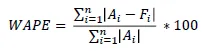
분모의 실제값을 평균(실제값)으로 대체, 실제값이 아닌 데이터의 전체 규모를 반영
sMAPE, Symmetric MAPE
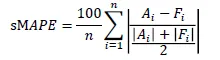
분모의 실제값을 실제값과 예측값의 평균으로 대체
-
상하한 값을 제한하여 오류율의 왜곡을 방지
-
분모값을 2로 나누어 주는지에 따라서 상하한 값은 0~1—%가 되거나 0~200%가 됨.
상항선이 200% 또는 100%로 제한할 수 있어 왜곡을 방지하고 이해하기 쉬움
- 튀는 이상치에 대한 반응정도 : 민감하지 않음
R-Squared, 결정계수
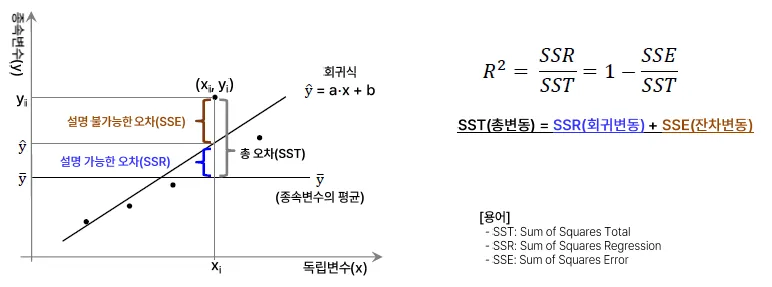
설명력, 적합된 회귀선이 주어진 데이터를 얼마나 잘 설명하고 있는가? = Goodness of Fit의 관점
-
결정계수가 높을수록 독립변수가 종속변수를 많이 설명함으로 해석(0~1)
-
Ex) R Squared 값이 0.6 : 원인변수의 분산이 결과변수의 분산을 60% 설명하고 있다.
평균: 어떤 사람이 평가를 내릴 수 있는 기준
SSR: 평균 대비하여 회귀선이 오차를 설명할 수 있는 정도
- 사용관점
| 항목 | 설명 |
|---|---|
| 모델 설명력 평가 | 전체 변동 중에서 모델이 설명한 비율을 수치로 나타냄 |
| 0~1 사이 값 | 1이면 완벽한 예측, 0이면 평균으로 예측한 것과 차이 없음 |
| 성능 비교 지표 | 여러 모델의 상대적인 설명력을 비교 가능 |
- 사용관점
| 비교 항목 | MAE / MSE | R² |
|---|---|---|
| 초점 | 오차의 크기에 초점 | 모델이 데이터를 얼마나 설명했는지에 초점 |
| 해석 | "얼마나 틀렸는가" | "모델이 얼마나 잘 설명했는가" |
| 단위 | 실제값의 단위와 같음 (MAE), 제곱 (MSE) | 단위 없음, 0~1 (또는 음수까지 가능) |
| 절대/상대 지표 | 절대적인 오차의 양 | 상대적인 설명력 |
| 이상치 영향 | MAE는 낮음, MSE는 높음 | 간접적으로 영향받음 (MSE 기반이므로) |
-
Train Data에 적합한 방법론임(Train Data에 대한 적합도)
-
음수값이 나오는 경우 : Out of Sample을 계산했을 경우
단변량 회귀를 하는 경우, 설명계수 = 상관계수의 제곱
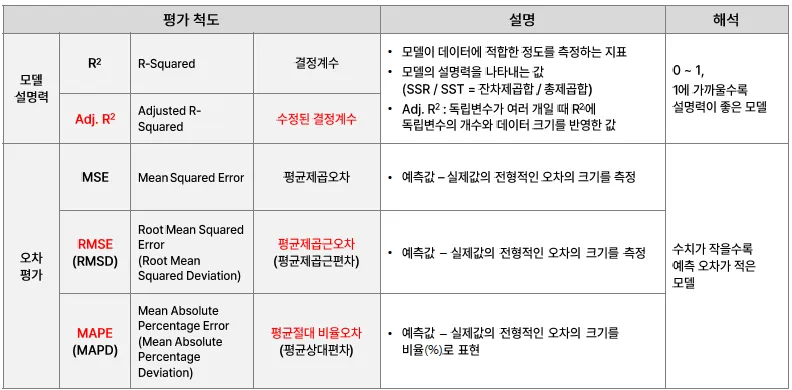
- 수정된 결정계수, Adj R squared
변수가 투입되는 경우 결정계수가 계속 커짐
⇒ 독립변수의 개수와 데이터 크기를 반영하여 결정계수를 계산함
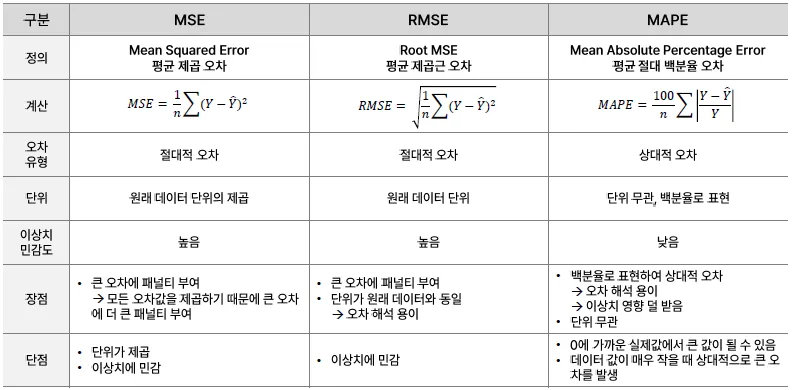
산출예시
- MSE
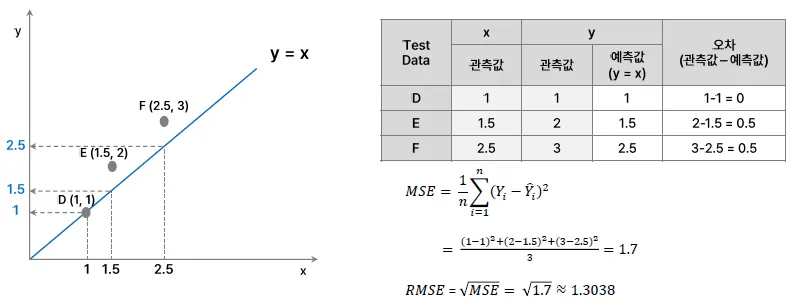
- MAPE
- sMAPE
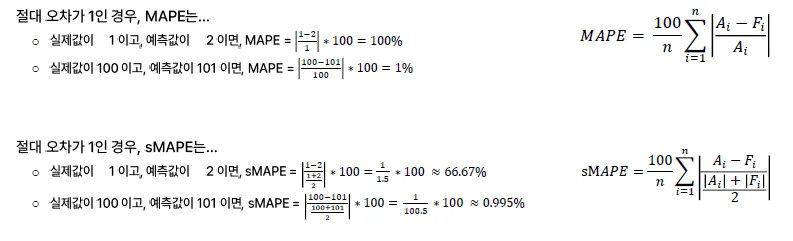
성능평가 유의점
-
성능 평가 기준을 먼저 정하고. 그에 맞는 평가지표를 기준으로 측정
-
모델 설명력은
-
Sample 크기와 변수의 개수를 고려하여 수정된 결정계수를 고려
-
결정계수에서 좋은 값에 대한 절대적인 기준은 존재하지 않음(절대 표준 X)
-
-
오차평가는
-
RMSE와 MAPE는 특별한 경우를 제외하면, 회귀모델에서 가장 유용하게 사용할 수 있는 지수
-
MAPE는 경우에 따라서 대체 지수로 비교해야 함
-
-
모델 성능은 Test Set의 평가에 더 해석 비중을 두어 진행함
(일반화 성능 평가, 과적합 방지, 모델 평가 정확성)
Classification Measurement
확률을 예측 → 임계치(Threshold)에 따른 분류
-
모델이 실제 데이터를 얼마나 잘 분류하는지 측정
-
분류 모델이 적용되는 도메인, 비지니스에 따라 적절한 성능지표는 달라짐에 유의
Case Study

-
해당 데이터에서 암환자에 대한 분류의 성능이 좋아야 함. (Critical 하므로)
-
또한, 하나의 class에 속한 data가 많은 경우 모든 데이터를 하나의 class로 예측하는 오류가 발생함
Confusion Metrics
실제값과 예측값의 비교 분류표를 뜻함
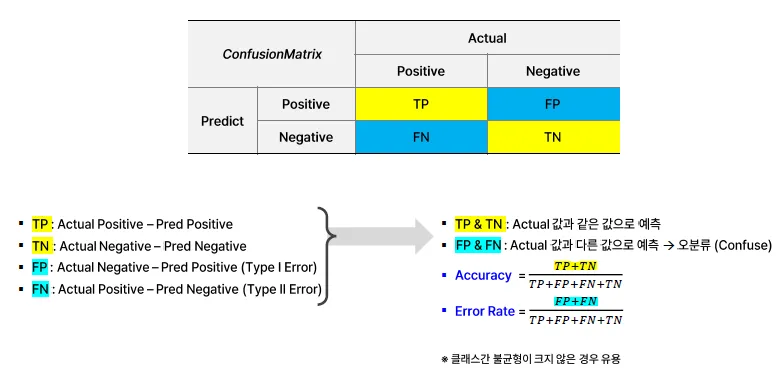
| 실제 / 예측 | Positive (1) | Negative (0) |
|---|---|---|
| Positive | TP | FN |
| Negative | FP | TN |
여기서 나오는 주요 지표들은:
-
정확도(Accuracy) = (TP + TN) / 전체
-
정밀도(Precision) = TP / (TP + FP)
-
재현율(Recall) = TP / (TP + FN)
클래스 불균형이 클 경우 (예: 99% Negative, 1% Positive)
-
모델이 무조건 Negative로만 예측해도
- 정확도는 99%
- 하지만 Positive는 하나도 못 맞춤 (TP=0, FN=100%)
-
이 경우 혼동 행렬 기반 정확도는 완전히 무의미
-
혼동 행렬 기반 지표들은 각 클래스가 비슷한 비율일 때:
- TP, FP, FN, TN이 고르게 나오기 때문에
- 정확도나 정밀도, 재현율이 더 신뢰성 있게 계산됨
즉, 클래스 간 균형이 잡혀 있어야 실제로 전 클래스에 대해 잘 맞춘다는 의미가 됨.
불균형 문제를 다룰 때는 다음과 같은 지표를 더 선호함:
| 지표 | 설명 |
|---|---|
| F1 Score | 정밀도와 재현율의 조화 평균 (불균형에 조금 더 강함) |
| ROC-AUC | 클래스 비율 무관하게 전체적인 분류 능력을 평가 |
| PR Curve (Precision-Recall Curve) | 특히 Positive 클래스가 희귀한 경우 더 유용 |
| Balanced Accuracy | 각 클래스의 정확도를 평균 |
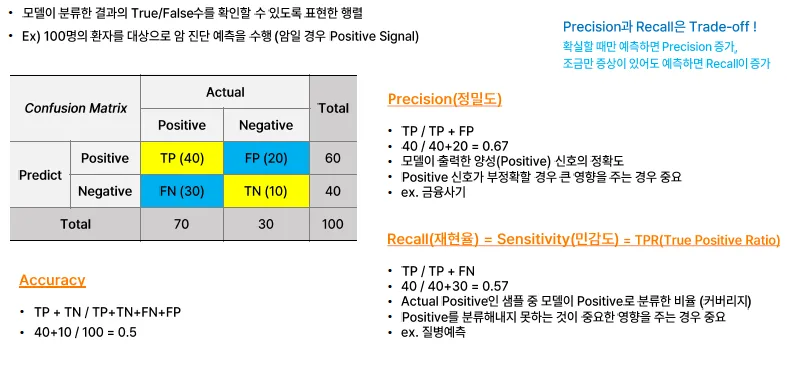
Precision과 Recall
두 개의 값은 Trade-off 관계를 가짐
- Precision
모델이 출력한 Positive의 정확성(Positive라고 예측한 것 중에 실제 Positive인 경우)
→ 확실할 때만 예측하면 Precision이 증가
- Recall = Sensitivity
실제 Positive인 것 중에 Positive로 예측한 경우
→ 증상이 조금만 있어도 True로 예측하면 Recall이 증가
→ 질병예측과 같이 Positive로 분류하는 것이 중요한 경우에 성능이 좋아야 함

Specificity, 특이도
실제 Negative인 경우 중에 Negative로 예측한 경우
- 제 1종 오류(알파)
Positive라고 예측했지만, 실제로는 Negative일 경우
- 제 2종 오류(베타)
Negative라고 예측했지만, 실제값은 Positive일 경우
F1-Score
precision과 Recall의 조화평균 (역수의 산술평균의 역수)
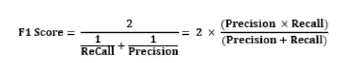
불균형한 데이터에서 잘 동작하며, 단편적인 성능이 아닌 종합적으로 보기 위함
-
조화평균을 사용하는 이유
- Precision, Recall 둘 중 하나가 극도로 낮을 때에도 지표에 그것이 잘 반영되도록 하기 위해
- 두 지표를 모두 균형있게 반영하기 위해
조화평균
ROC Curve, Receiver Operating Characteristic Curve
다양한 임계값 설정에서 분류 모델의 성능을 평하기 위해 사용됨
-
ROC 커브가 좌상단에 붙을수록 더 좋은 분류기를 의미
-
ROC 곡선은 클래스 분포의 변화에 불변
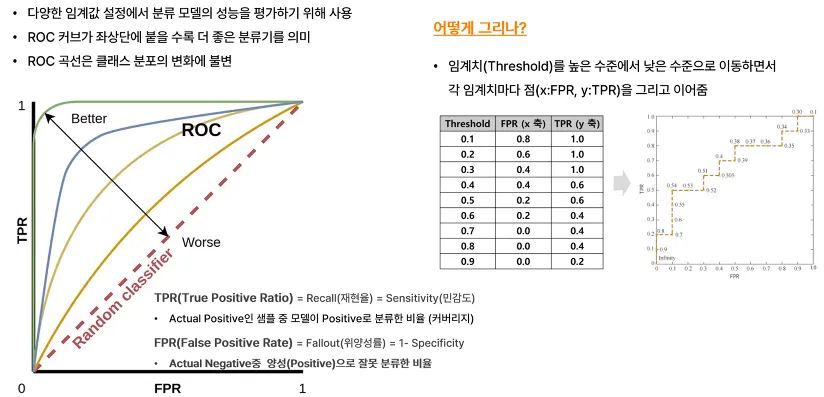
(분모) = FPR, 실제 NEGATIVE라고 예측한 것 중 POSITIVE로 예측한 비율
(분자) = TPR, 실제 POSITIVE인 것 중에 POSITIVE로 예측한 비율
위의 표에서 임계치가 작다는 것은 모두 Positive로 예측함을 의미해서, Recall값이 높아짐
AUROC, Area Under ROC Curve
ROC Curve 아래 면적을 통해서 모델성능을 하나의 수치로 정량화(0.8부터 좋은 값)
-
샘플의 분포가 변화하더라도 급격한 변화 X
-
안정적으로 모델 성능을 테스트할 수 있음

PR Curve를 사용하지 않고, ROC Curve를 사용하는 이유
보통 맞추고 싶은 데이터는 소수인데, PR Curve는 데이터에 대한 불균형 정도가 조금만 바뀌어도 Line이 확 바뀜.
→ 선이 확 바뀌는 이유는 Precision의 모수가 굉장히 적으므로(맞추고 싶은 target) 숫자가 크게 변화하게 됨.
→ 틀린 개수를 확인하게 되면, 데이터의 수가 많아져서 값의 변화가 작음
Log Loss
맞춘 결과로 성능을 평가하지 않고, 예측의 확신 정도(확률)을 반영하여 평가.
→ 확신의 정도가 낮을수록 페널티(Loss)값이 증가함
확률의 크기는 0~1 사이인데, log의 범위는 (0~1 사이에서) 음수의 값을 가지므로 이를 처리함
결론
F1-score
F1-score는 하나의 precision과 하나의 Recall이 사용됨
→ 적당한 임계치를 알고 있는 경우에는 F1-Score를 사용하는 것이 적절함.
AUROC
AUROC는 여러 개의 임계치를 사용하여 비교할 수 있음
→ 임계치에 상관없이 전반적인 경향을 확인할 수 있음.
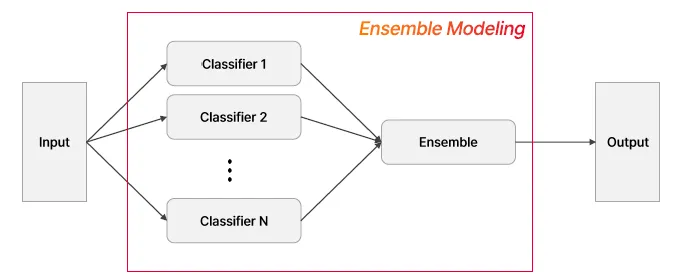
Ensemble Modeling
Ensemble
하나의 모델이 아닌, 여러 개의 모델을 생성하고 결합하여 좀 더 정확한 예측을 도출
-
단일 모델의 약점을 다수의 모델들을 결합하여 보완
-
성능이 떨어지더라도 서로 다른 유형의 모델을 섞는 것이 오히려 전체 성능에 도움이 될 수 있음
-
Decision Tree의 단점인 과적합은 여러 모델을 결합하고 보완하여, 알고리즘 자체의 장점인 직관적인 분류를 강화할 수 있음
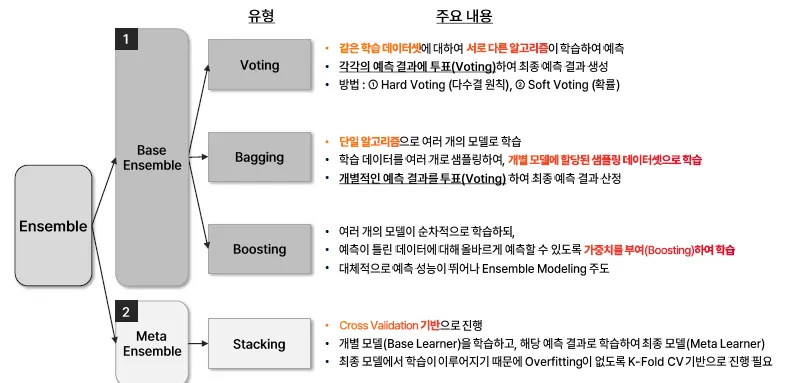
Ensemble 유형
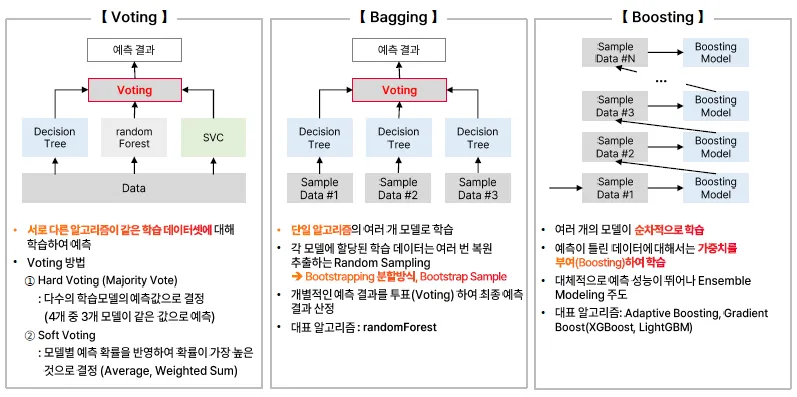
Voting
같은 학습 데이터셋에 대하여 서로 다른 알고리즘이 학습하여 예측하고, 이를 투표하여 결과 생송
-
Hard Voting(다수결)
-
SOft Voting(확률)
Bagging
단일 알고리즘으로 여러 개의 모델로 학습, 학습데이터를 여러 개로 샘플링하여 개별 모델에 할당된 샘플링 데이터셋으로 학습을 진행
Boosting
여러 개의 모델이 순차적(Sequential)으로 학습하되, 가중치를 부여하여 학습
앞에서의 오차를 수정할 수 있도록 뒤의 모델에서 다시 학습 및 예측함
Stacking
Cross Validation 기반으로 진행하며, 개별 모델을 학습하고 해당 예측 결과로 학습하여 최종 모델(Meta Learner)
→ 최종 모델에서 학습이 이루어지기 때문에 Overfitting이 없도록 K-Fold CV 기반으로 진행 필요
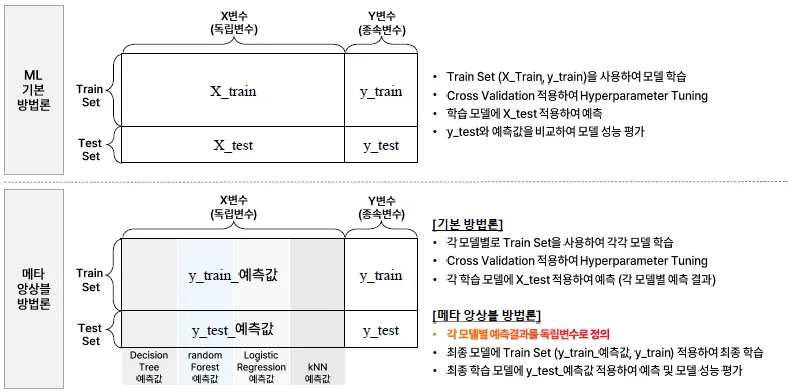
Meta Ensemble
메타 앙상블은 기본 모델들의 예측을 독립변수로 활용하여 최종 예측을 수행하는 기법으로, Overfitting 이슈로 신중하게 고려해야 함.
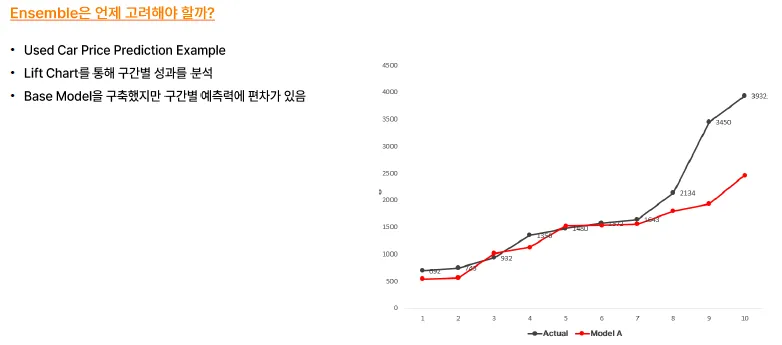
Case Study
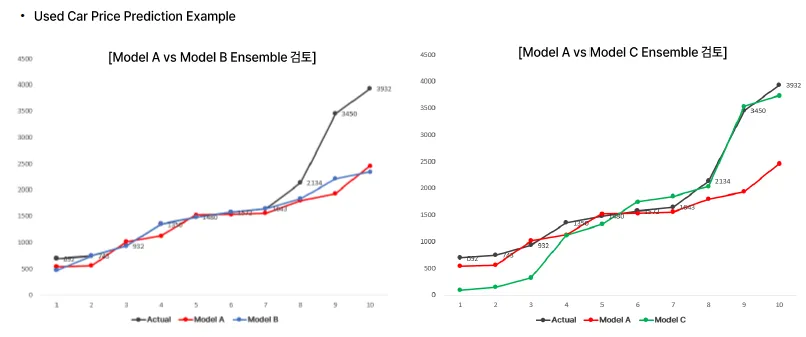
- 구간마다 몇 개씩 맞췄는지의 개념으로 접근할 수도,,,

단일 모델로는 특정 구간에서의 예측이 좋지 않을 경우, 앙상블 모델을 활용해서 해당 구간에 대해 성능을 높일 수도 있음
모델 최적화
모델의 학습과정에서 성능지표를 개선하기 위해 파라미터를 조정하고, 모델을 조정하여 최상의 성능을 얻는 과정
-
성능 향상: 모델이 정확하게 예측하고 좋은 성능을 발휘하도록 조정
-
일반화 향상: 새로운 데이터에 대해 잘 작동하도록 모델 개선
-
효율성 증가: 학습 과정의 속도를 높이고, 계산 자원을 효율적으로 사용
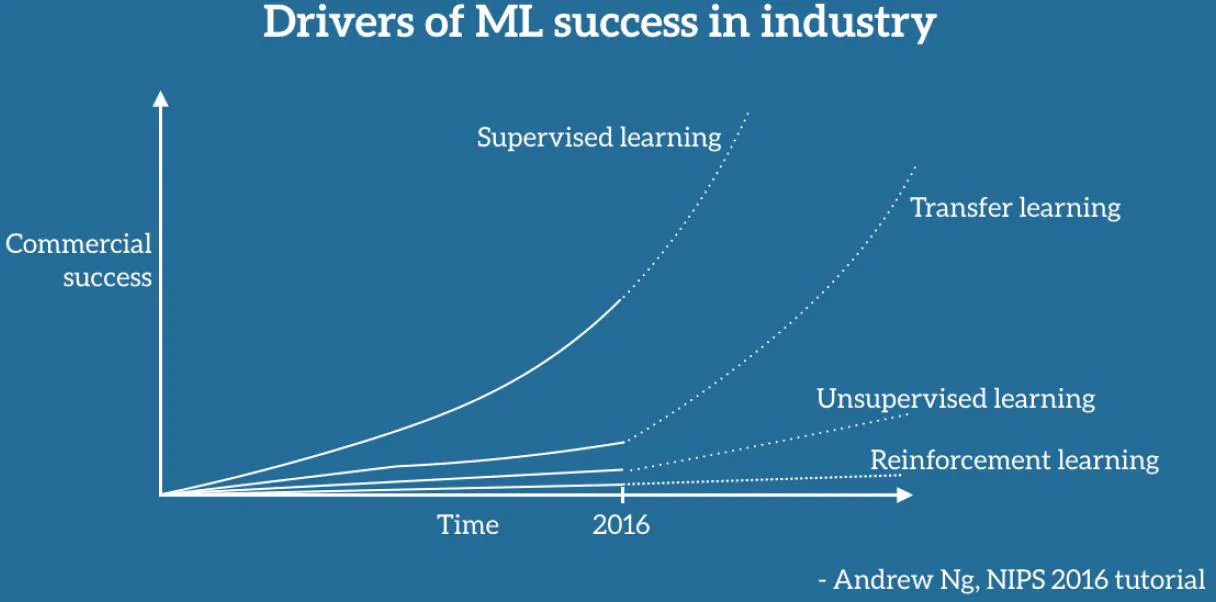
Transfer Learning, 전이학습
누군가 학습시켜 놓은 성능 높은 모델을 활용하여 내가 가진 데이터에 맞는 모델로 커스터마이징
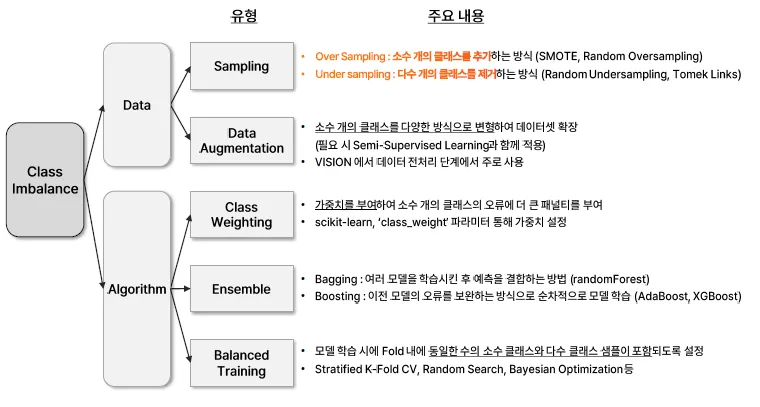
데이터 관점에서 최적화 방안
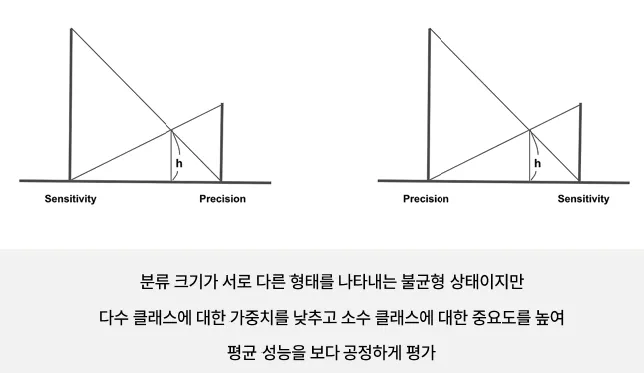
데이터 불균형
편향이 없도록 학습한 모델이 실제 9:1의 데이터를 만나더라도, 더 잘 예측할 수 있다는 믿음
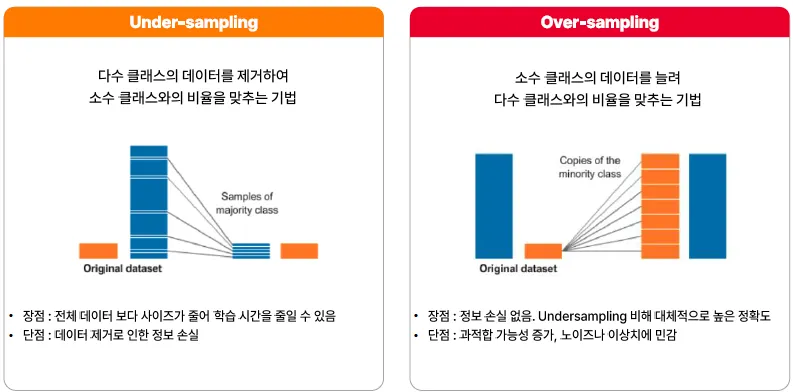
- 불균형한 데이터를 균형을 이루도록 맞춰주는 방법
구분 설명 Over Sampling 소수 클래스 샘플을 추가하는 방식예: SMOTE, Random Oversampling Under Sampling 다수 클래스 샘플을 제거하는 방식예: Random Undersampling, Tomek Links Data Augmentation 주로 비정형 - 목적 소수 클래스 데이터를 다양한 방식으로 변형하여 데이터셋 확장 - 특징 필요 시 Semi-Supervised Learning과 함께 적용 - 주요 사용 분야 VISION 분야에서 데이터 전처리 단계에서 주로 사용
현장에서는 주로 Sampling 과정에서 Over, Under Sampling을 많이 사용함
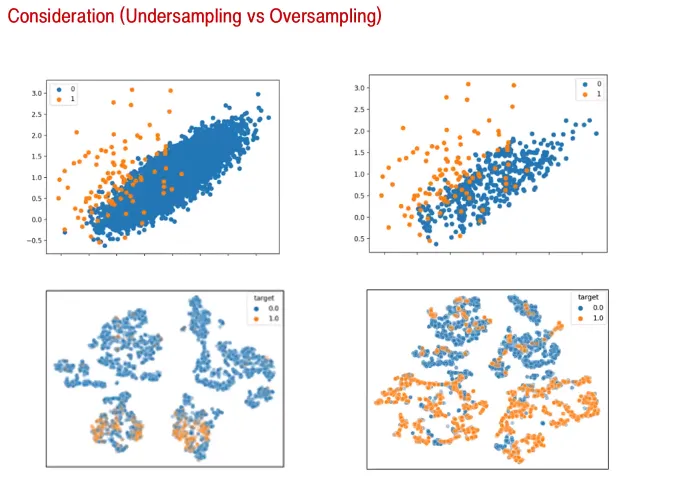
현장에서는 주로 Over-Sampling을 사용하는 경우가 많음
⇒ 작업자의 역량을 과시할 수 있기에..
Sampling을 잘했다는 기준은…?
-
숫자를 통해서 확인
-
시각화를 통해서 확인
⇒ 결국 Decision Boundary를 그리는 과정이므로, 최소한 결정경계가 손해를 보면 안됨.
- 위의 그림은 Under Sampling
시각적으로는 결정경계에서의 손해가 없어보임
- 아래 그림은 Over Sampling
시각적으로 결정경계가 모호해짐. 즉, 결정경계에서 손해가 생김
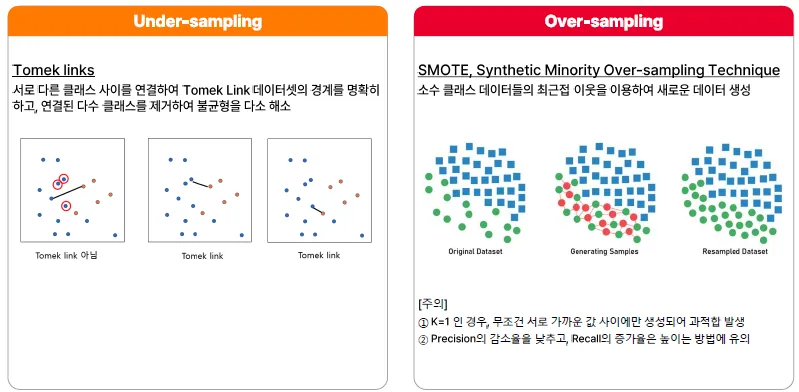
Tomek Link
-
각각의 점들에서 가장 가까운 점을 찾았을 때, 다른 Class이면 Tomek Link가 되어 연결됨 (3번째 그림이 적합)
-
이렇게 연결된 쌍들에 대해서 소수 class 쪽으로 class를 바꾸어버림
→ 소수 class가 Tomek link의 수만큼 늘어남, 경계가 선명해지는 효과
또는, 다수의 class를 날려버리는 방법도 있음
단점: 너무 많이 사용하면, 문제를 과하게 단순화한다는 점이 있음(과소적합)
SMOTE
- 소수 class들에 대해서 선을 긋고 사이에 데이터를 생성하는 방법론
단점: 똑같은(비슷한) 데이터를 복제하여 과적합되는 문제가 생길 수 있음
데이터 관점에서 최적화 방안
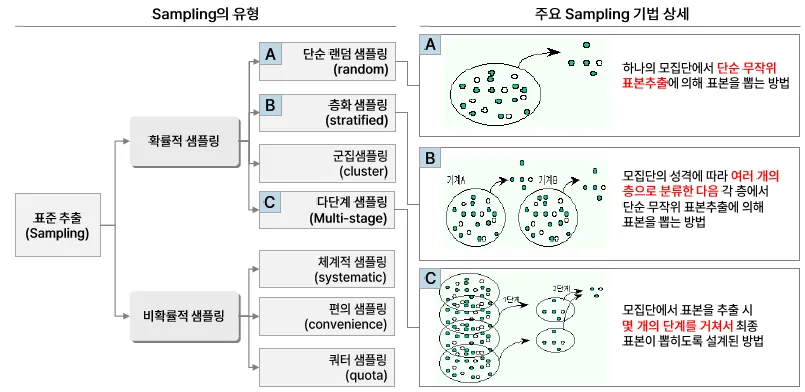
Sampling은 표본집단이 모집단의 특성을 반영하도록 표본을 추출하는 방법
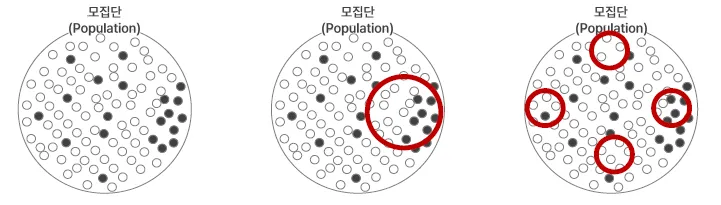
샘플링 편향, Sampling Bias
특정 데이터가 다른 데이터들보다 우선적으로 추출되어 발생하는 편향
-
표본은 모집단을 대표해야한다.
-
내가 가지고 있는 데이터(표본)이 전체 비지니스를 대변해야 함.
모델 관점에서 최적화 방안
배포된 모델이 기존 학습 데이터와는 다른 분포를 보이는 데이터로 모델 성능이 하락할 때 지속적인 모델 유지보수 필요
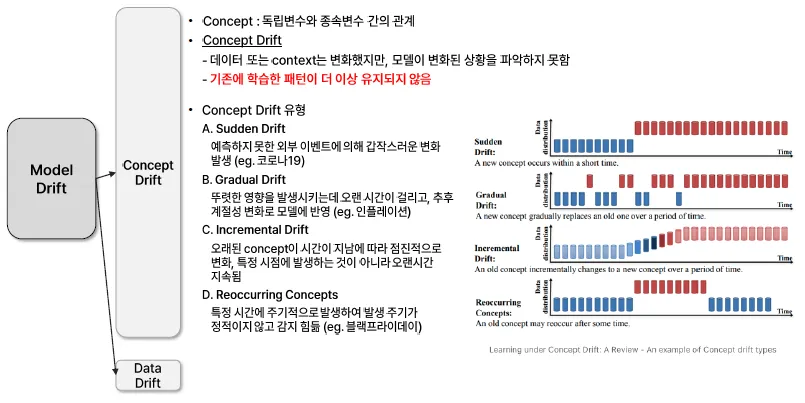
Concept Drift

| 유형 | 설명 | 예시 |
|---|---|---|
| Sudden Drift | 예측하지 못한 외부 이벤트로 인해 갑작스러운 변화 발생 | 코로나19 |
| Gradual Drift | 뚜렷한 영향은 있으나 오랜 시간에 걸쳐 점진적으로 변화 반영 | 인플레이션 |
| Incremental Drift | 오랜 시간 동안 지속적이고 서서히 변화, 특정 시점에 급격한 변화 없음 | - |
| Reoccurring Concepts | 일정한 주기가 없고, 비정기적으로 반복 발생하는 개념 변화 | 블랙프라이데이 |
(Reoccurring Concepts)는 Promotion과 같은 성격을 가짐
Data Drift
모델이 충분히 학습하지 못한 데이터가 있는 경우
| 유형 | 설명 | 예시 |
|---|---|---|
| Covariate Shift | Input 분포가 변하는 현상 | - 주요 고객층이 2030에서 4050대로 변화. 기존 모델은 2030을 대상으로 학습하여 4050대에 대해 예측 성능이 낮음 |
| Prior Probability Shift | Target 분포가 변하는 현상 | - 특정 제품의 구매율이 10% → 30%로 증가. 추천 시스템이 이 변화 반영 못 해 성능 저하. 신제품 등장 시 모델이 반영 못함 |
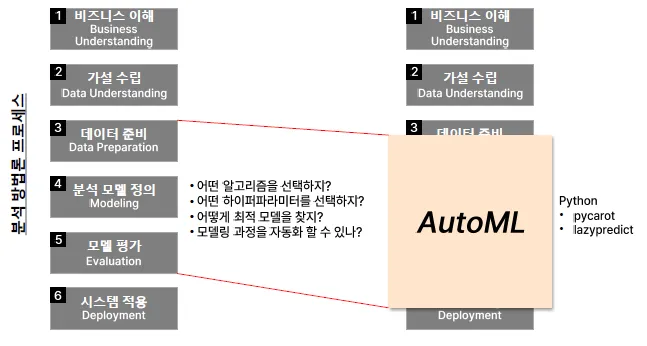
AutoML
머신러닝 모델을 학습하고 배포하는 과정을 자동화하는 기술 또는 도구
→ 다양한 알고리즘을 실험하고 하이퍼파라미터 비교를 통해 최적의 모델을 찾는 과정을 자동화
