AI
AI를 구현하는 방법에는 여러가지가 존재합니다.

우리는 이 중에서 머신러닝(Mechine Learning 통칭 ML)에 대해 이야기를 하고자 합니다.
ML(Mechine Learning)
프로그래밍 방식
먼저 기존 프로그래밍 방식은 Rule-based 방식으로 규칙에 기반한 방식으로 프로그래밍이 됩니다.
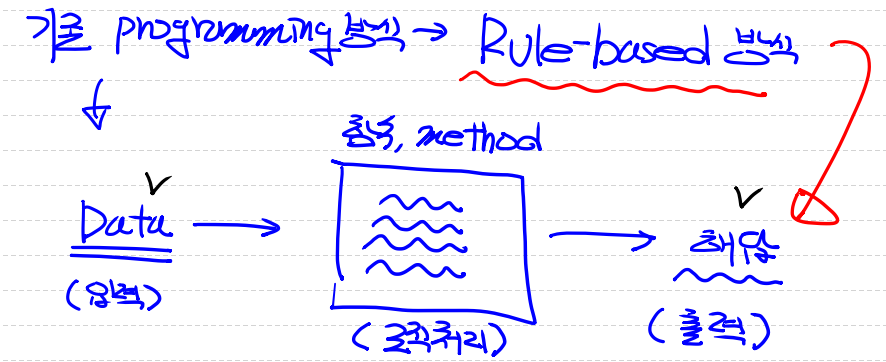
Data(입력) => 함수와 Method를 통한 로직처리 =>해답(출력)을 하게 됩니다.
머신러닝 방식
그에 반해 머신러닝은 다른 방식을 사용하게 됩니다.
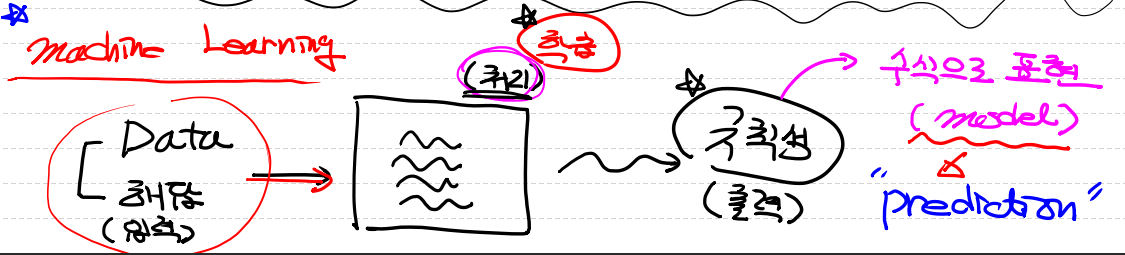
Data,해답(입력) 모두 입력 데이터에 같이 들어가게 되고,
학습에서는 Query를 통과 후 규칙성을 출력하게 됩니다.
이 규칙성이 인공지능에서 필요한 Model이 생성되게 됩니다.
이 Model은 수식으로 표현이 되고 다른말로는 Prediction 예측이라고도 합니다.

한 줄로 표현하자면 입력안에는 Data와 해답이 모두 존재하고 이것을 학습을 진행 => 데이터를 일반화하는 Model이 생성되게 됩니다.
여기서 학습이란 => 데이터와 정답간의 규칙성을 찾아내는 작업입니다.
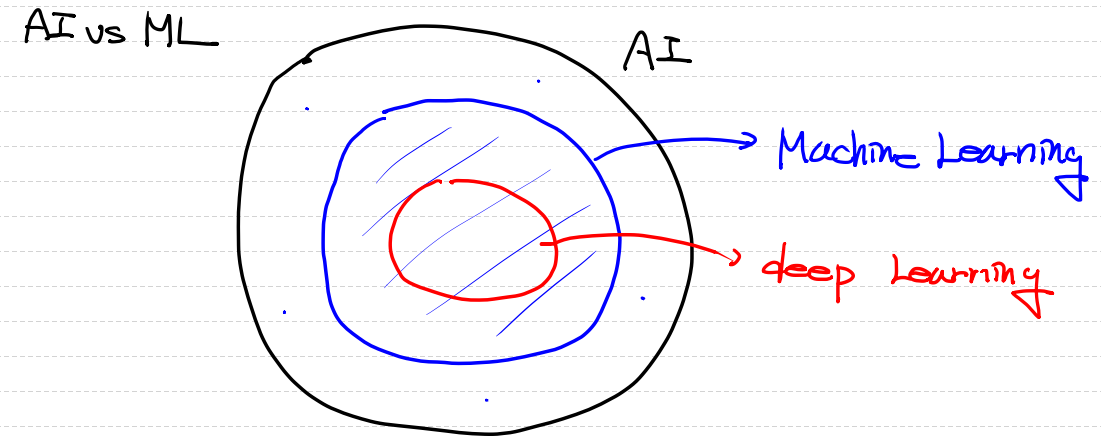
ML과 DL
흔히 우리가 말하는 딥러닝 Deep Learning(DL)은 크게 머신러닝안에 포함되어 있습니다.
ML과 DL의 차이점은 Data의 특성이 다르다는 것입니다.
ML은 정형 데이터를 사용하고
DL은 비정형 데이터를 사용하게 됩니다.
머신러닝 알고리즘
머신러닝의 알고리즘에는 다양한 많은 것들이 존재합니다
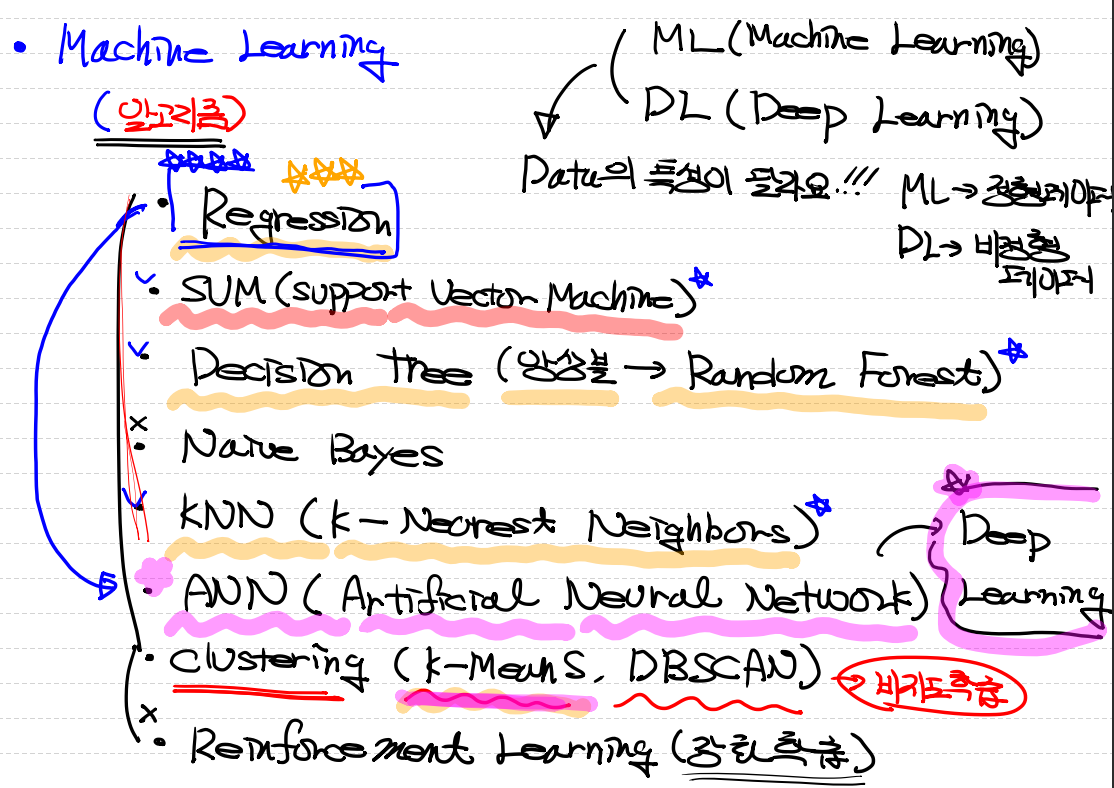
- Regression
- 회귀로 여러가지가 존재한다.
- SVM(Support Vector Mechine)
서포트 벡터 머신- 패턴 인식, 자료 분석을 위한 지도 학습 모델이며, 주로 분류와 회귀 분석을 위해 사용한다
- Decision Tree
의사결정 트리(앙상블 기법 적용 -> Random Forest)- 의사결정나무는 분류(classification)와 회귀(regression) 모두 가능합니다
- Naive Bayes
나이브 베이즈 - KNN(K - Nearest Neighbors)
K-최근접 이웃 - ANN(Artificial Neural Network)
인공 신경망=> Deep Learning에 주로 사용 - Clustering (K-Means, DBscan) => 비지도학습
- Reinforcement Learning
강화학습
머신러닝 타입
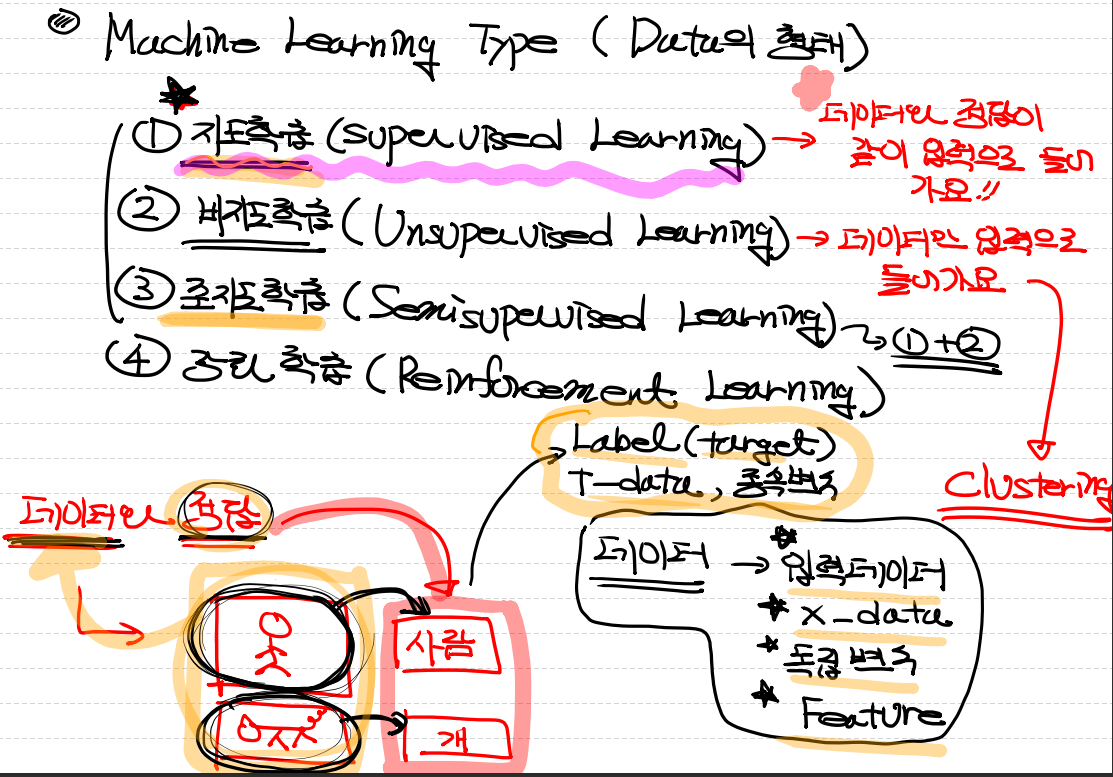
- 지도학습(Supervised learning)
- 데이터와 정답이 같이 입력으로 들어갑니다.
- 비지도 학습(Unsupervised learning)
- 데이터만 입력으로 들어감 => clustering 과정을 거침
- 준지도학습(Semisupervised learning)
- 지도학습과 비지도학습을 합친것
- 강화학습(Reinforcement Learning)
- 데이터
- 입력데이터
- X_data
- 독립변수
- Feature
- 정답
- label
- target
- T_data
- 종속변수지도학습(Supervised Learning)
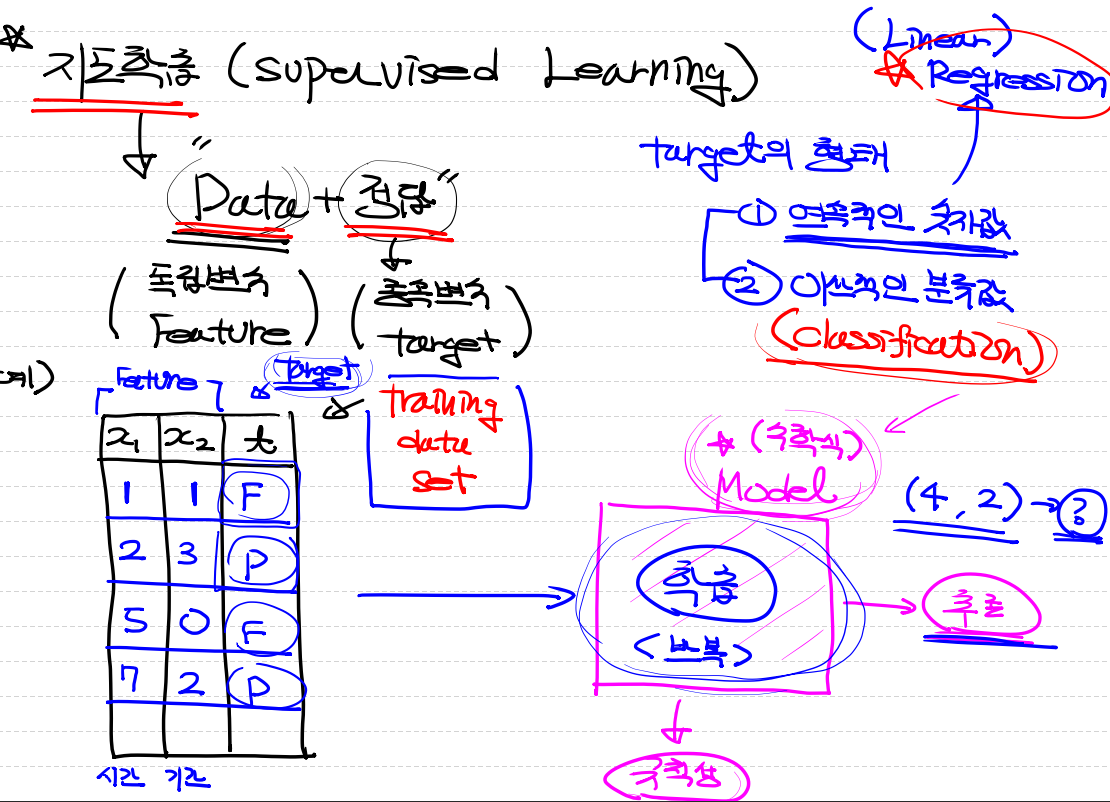
지도학습은 Data(독립변수) + 정답(종속변수)이 입력값이다
이 입력값을 위의 그림처럼 학습을 반복하여 규칙성을 찾아낸다.
이 규칙성이 Model이며 최종적으로 모델이 저장된다.
여기서 Target의 형태는 두가지로 나뉜다.
- 연속적인 숫자값일때 => (Linear Regression)
- 이산적인 분류값일때 => (Classification)
회귀(Regression)

- 회귀 : 어떤 데이터에 대해 그 데이터에 영향을 주는 조건들의 평균적인 영향력을 이용해서 데이터에 대한
조건부 평균을 구하는 기법이다.
==> 아주 간단하게 생각하면 회귀는평균을 구하는 기법이다.
회귀 예시
예를 들어보겠습니다.
ex) 우리나라의 아파트 시세가 얼마인지 조사 -> 아파트 시세를 나타내기위한 대표값은 어떤게 적절할까?
평균, 최대, 최소, 중위, 최빈 값을 사용한다.
ex) 우리나라의 아파트 시세가 얼마인지 조사 -> 아파트 시세를 나타내기위한 대표값은 어떤게 적절할까?
산출평균으로 계산한다 ==> `1억`
아파트 가격에 영향을 주는 요인이 굉장히 많습니다.
ex) 평수, 연식, 학군, 지역, 층수, 방향, 역세권 등등조금 더 자세하게 특정 조건에 따른 가격 변화(면적)를 보겠습니다.
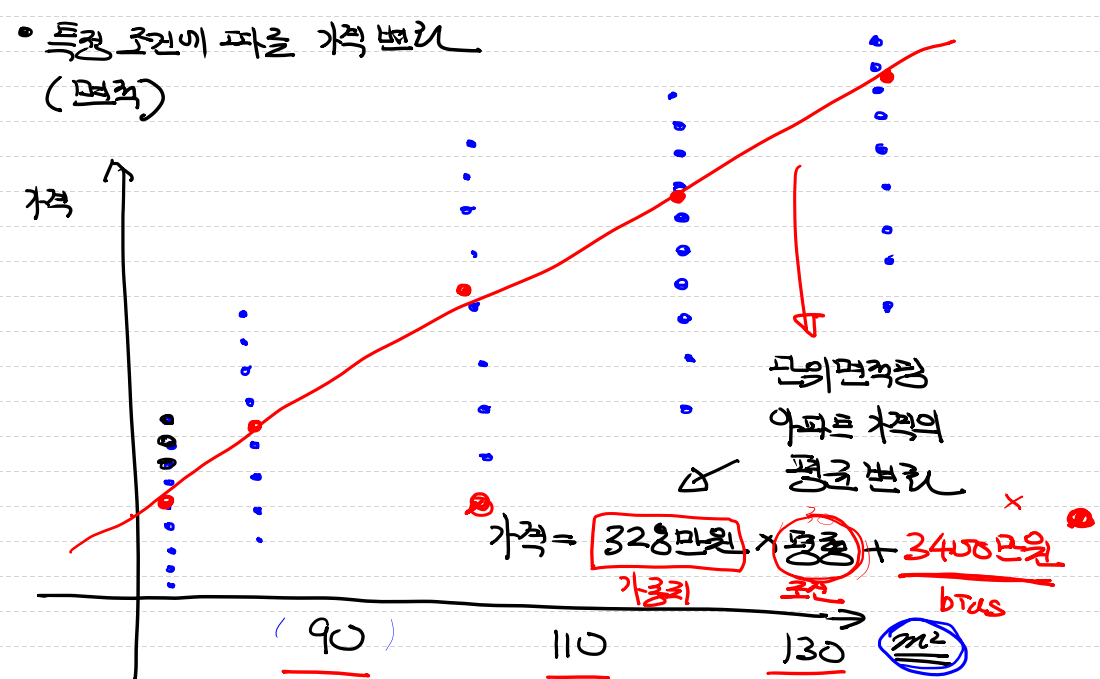
가격이 파란색 점으로 형성되어있다고 가정하면 면적의 평균은 빨간색 점이다.
여기서 점은 예를 들어 328만원 * 평형 + 3400만원 이라고 가정하면
328만원(가중치) 평형(조건) 3400만원(bias)라고 표현할 수 있다.
아파트 가격은 조건에 따라 또 추가가 되기 때문에 여러 요인들을 더해야합니다.
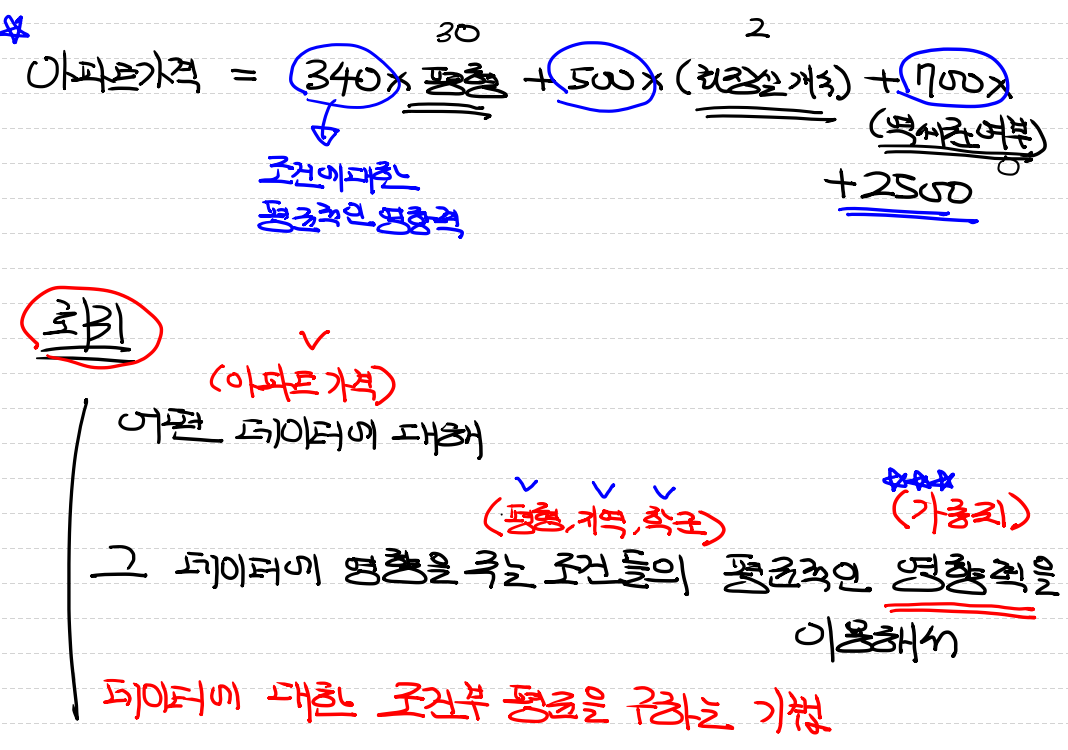
아파트 가격 = 340(평형) + 500(화장실 개수) + 700*(역세권여부) + 2500
여기서 340, 500, 700은 가중치(W) 평형, 화장실 개수, 역세권 여부는 조건 2500은 bias로 표현할 수 있다.
즉 회귀란 어떤 데이터(아파트 가격)에 대해 그 데이터에 영향을 주는 조건(평형,지역,학군)들의 평균적인 영향력(가중치)를 이용해서 데이터에 대한 조건부 평균을 구하는 기법이다.
회귀 그래프
여기서 우리가 구하고 싶은건 가중치(W), 보정치(Bias)이다.
단순화시켜서 생각을 하게 되면 독립변수가 한개일때는 아래와 같은 직선식이 그려지게 된다.
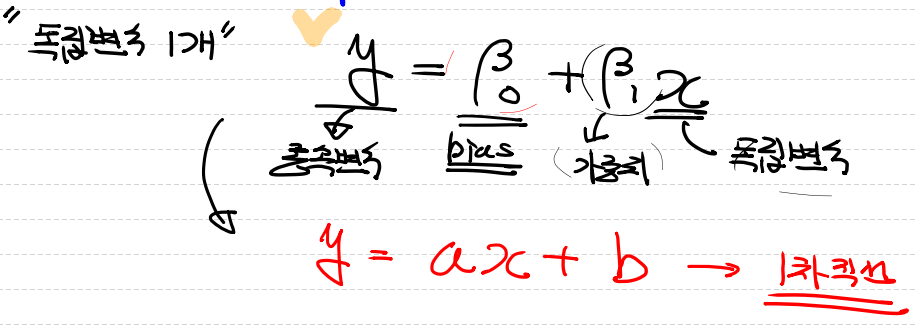
회귀를 할때 알아두어야하는 사항
-
회귀는 평균적으로 평균을 구하는 기법이다.
-
- 우리나라 근로자의 연봉 => 대체적으로 살짝 기울여진 그래프
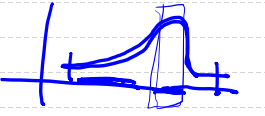
- 우리나라 근로자의 연봉 => 대체적으로 살짝 기울여진 그래프
-
- 우리나라 성인 남자의 키 => 정규분포와 비슷한 모양의 그래프
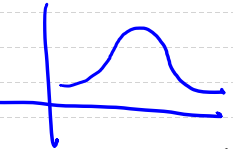
- 우리나라 성인 남자의 키 => 정규분포와 비슷한 모양의 그래프
-
-
Regression toward the mean
- 많은 자료를 토대로 결과를 예측할 때 그 결과 값이 평균에 가까워지려는 경향성을 가진다.
- 이것은 상관이 완전하지 않은 관게에서도 볼 수 있는 특성이다.
-
종속변수의 개수에 따라 모델이 달라집니다.
- 단변량 회귀모델
- 다변량 회귀모델
- 기본적으로 회귀분석은 단변량을 가정하고 있습니다.
-
굉장히 많은 회귀 모델의 종류가 존재합니다.
- 그 중에서 우리가 사용하고 연습할 모델은 가장 기본적인 모델인
Classical Linear Regression Model이고 일반식은 아래와 같습니다.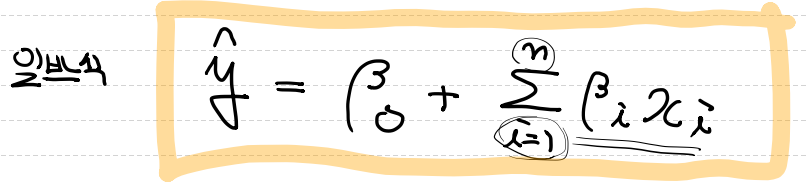
- 그 중에서 우리가 사용하고 연습할 모델은 가장 기본적인 모델인
파이썬 구현
파이썬 수치 미분 코드
# 일변수 함수의 수치미분 코드 구현
# 입력으로 함수를 받아서 미분을 수행하는 함수를 하나 구현해 봅시다!
# 우리 파이썬은 일급함수를 지원합니다!
# 함수의 인자로 다른 함수를 받을 수 있습니다.
def numerical_derivative(f, x):
# 입력인자 f는 미분하려는 함수
# 입력인자 x는 미분값을 알고자하는 입력값.
delta_x = 1e-4
# 중앙차분을 이용한 미분을 코드로 표현해봅시다!
result = (f(x + delta_x) - f(x - delta_x)) / (2 * delta_x)
return result
# 이 미분함수가 정상적으로 값을 계산하는지 확인해 봅시다!
def my_func(x):
return x**2
# 함수 f(x) = x**2의 미분계수 f'(5)를 구해봅시다!
result = numerical_derivative(my_func, 5)
print(result) # 9.999999999976694# 다변수 함수의 수치미분 코드를 구현해보아요!
# f(x,y)=2x+3xy+y^3제곱
# x에 대해 편미분 => 2+3^y
# y에 대해 편미분 -> 3 + 3y^2
# f'(1.0, 2.0)=?
# x에 대해 미분이기에 x자리의 값은 x에 대한 편미분
# y도 마찬가지
# 각각 집어넣게되면 (8.0, 15.0)이 나옴
import numpy as np
def numerical_derivative(f, x): # x가 다변수함수이기때문에 2개가 들어가야함
# f: 미분하려고하는 다변수 함수
# x: 모든 변수를 포함하는 ndarray [1.0, 2.0] ==> 2변수
# 미분의 결과는 [8.0, 15.0]이 나와야함.
delta_x =1e-4
derivative_x = np.zeros_like(x) # [0.0, 0.0]
it = np.nditer(x, flags=['multi_index'])
while not it.finished:
idx = it.multi_index # 현재의 index를 추출 => tuple형태로 리턴
tmp = x[idx] # 현재 index의 값을 일단 잠시 보존해요.
# 밑에서 이 값을 변경해서 중앙차분 값을 계산해야함
# 그런데 우리 편미분을 해야하는데 다음 변수 편미분을 할때에
# 원래값으로 복원해야 정상적으로 진행되기 때문에
# 이 값을 잠시 보관했다가 원상태로 복구해야함
x[idx] = tmp + delta_x
fx_plus_delta_x = f(x) # f(x + delta_x)
x[idx] = tmp - delta_x
fx_minus_delta_x = f(x)
derivative_x[idx] = (fx_plus_delta_x - fx_minus_delta_x) / (2 * delta_x)
x[idx] = tmp
it.iternext()
return derivative_x
def my_func(x):
return x**2
# f'(3.0)을 구해보아요!
result = numerical_derivative(my_func, np.array([3.0]))
print(result) # 6# 2변수 함수를 다시 만들어보아요!
def my_func(input_data):
x = input_data[0]
y = input_data[1]
# f(x) = 2x + 3xy + y^3
return 2*x + 3*x*y + np.power(y,3)
result = numerical_derivative(my_func, np.array([1.0, 2.0]))
print(result) # [ 8. 15.00000001]# 4변수 함수에 대해서 수치미분을 해보세요
def my_func(input_data):
w = input_data[0,0]
x = input_data[0,1]
y = input_data[1,0]
z = input_data[1,1]
# f(x)=2x+3xy+y^3
return w*x + x*y*z + 3*w + z*np.power(y,2)
data = np.array([[1.0, 2.0],
[3.0, 4.0]])
result = numerical_derivative(my_func, data) # np.array가 들어가야하니까 아예 np.array로 리스트를 생성해서 만듬
print(result) # [[ 5. 13.]
# [32. 15.]]