백준 / 11404 / 플로이드 / python

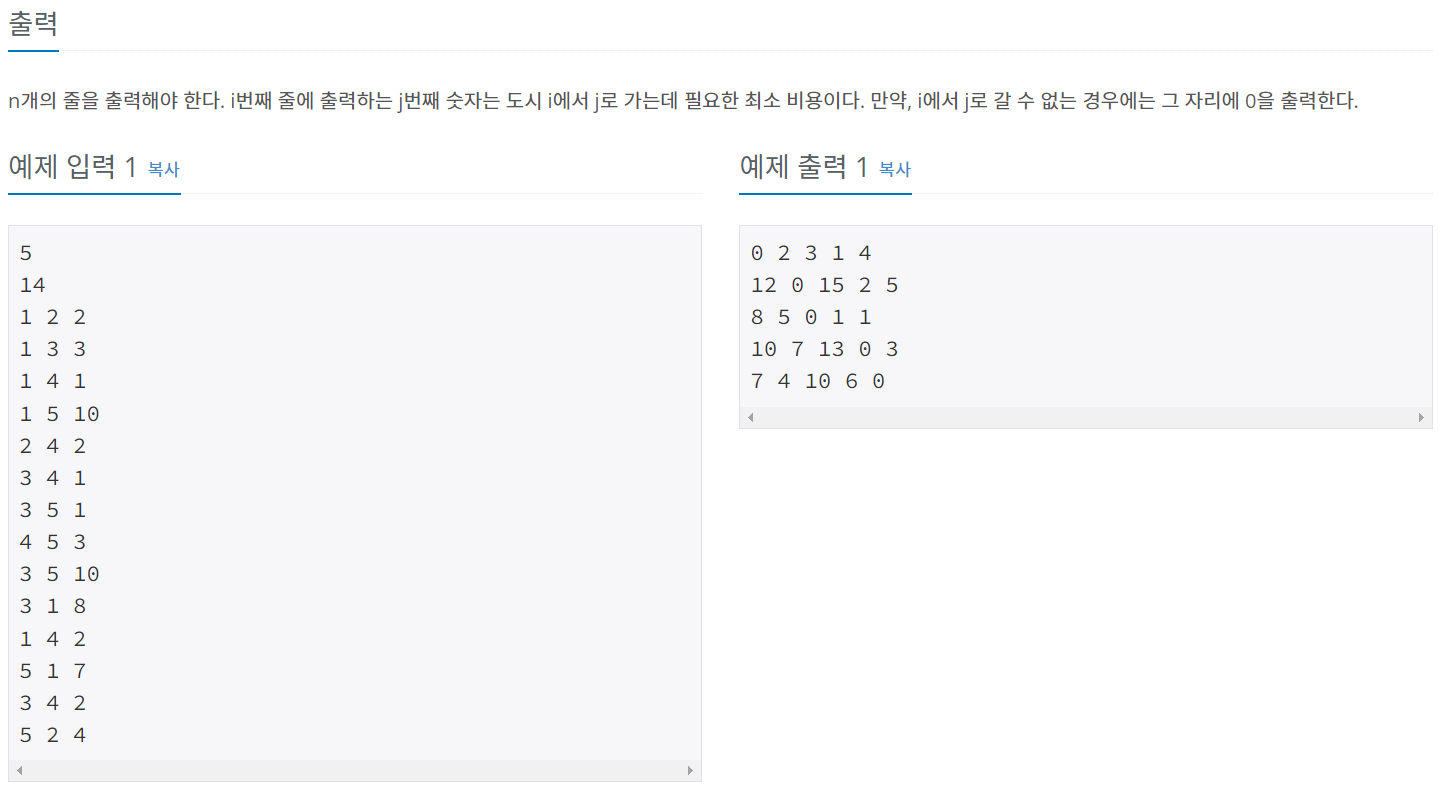
다익스트라 풀이

import sys
input = sys.stdin.readline
from heapq import heappop, heappush

def dijkstra(start):
    dist = [1e9] * (n+1)
    dist[start] = 0

    h = []
    heappush(h, (0, start))

    while h:
        dis, node = heappop(h)

        if dist[node] < dis:
            continue

        for next_node, next_dis in graph[node]:
            d = dis + next_dis
            if dist[next_node] > d:
                dist[next_node] = d
                heappush(h, (d, next_node))

    for i in range(1, n+1):
        if dist[i] == 1e9:
            dist[i] = 0

    return dist[1:]

n = int(input())
m = int(input())

graph = [[] for _ in range(n+1)]

for _ in range(m):
    a, b, c = map(int, input().split())
    graph[a].append((b,c))

for i in range(1, n+1):
    print(*dijkstra(i))

플로이드 와샬 풀이

import sys
input = sys.stdin.readline

n = int(input())
m = int(input())

dist = [[1e9] * (n+1) for _ in range(n+1)]

for _ in range(m):
    a, b, c = map(int, input().split())
    dist[a][b] = min(c, dist[a][b])

for k in range(1, n+1):
    for i in range(1, n+1):
        for j in range(1, n+1):
            if i != j:
                dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])

for i in range(1, n+1):
    for j in range(1, n+1):
        if dist[i][j] == 1e9:
            dist[i][j] = 0

for i in range(1, n+1):
    print(*dist[i][1:])

두개 알고리즘 메모리, 시간 비교

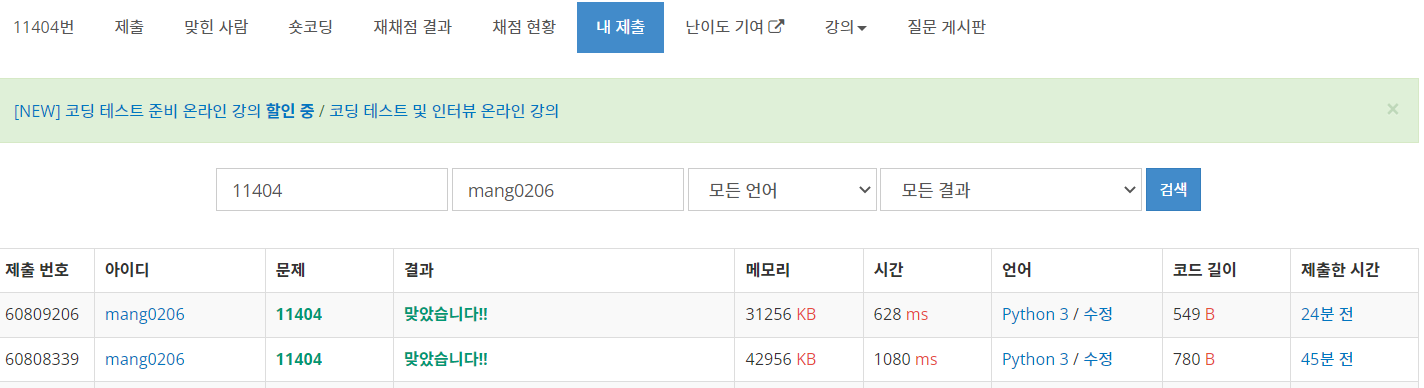
이 문제에서의 다익스트라 알고리즘의 시간 복잡도는 N^2 O(Elogn)이고 플로이드 와샬 알고리즘의 시간 복잡도는 O(n^3)이다.
이 문제의 경우 n의 크기가 E보다 적으므로 플로이드 와샬 알고리즘이 훨씬 유용하다. (이 처럼 모든 경로를 탐색하는데 노드의 갯수가 적은 문제는 플로이드 와샬 알고리즘을 사용하자!)

플로이드 와샬 알고리즘은 우선 모든 정점에 대해 최단 경로 정보를 2차원 list로 저장하며 처음에는 무한대 값으로 초기화 시켜준다.

간선 정보를 받을 때 해당 정보에 대해서 최소 값만 저장해 준다. (중복된 간선 정보가 있다면 최소 값만 저장한다)

그 다음 "floyd[a][b] = min(floyd[a][b], floyd[i][k] + floyd[k][j])" 점화 식을 통해 각 노드별 최단 경로를 구할 수 있다.

이 식에서 a는 시작점 b는 도착점 k는 경유지를 뜻 한다.

식의 의미를 풀이해보면 a를 출발해 b로 바로 가는 것보다
a를 출발해 k를 거쳐 b로 가는 게 효율적일 경우(저렴할 경우) 해당 값을 갱신해주는 것이다.
경로 k라 해서 하나의 정점 k만 거치는 것이 아니다. 여러 정점을 거치는 모든 경우의 수가 포함되어 있다.