백준 / 1956 / 운동 / python

import sys
input = sys.stdin.readline

v, e = [int(v) for v in input().split()]
dist = [[1e9]*(v+1) for _ in range(v+1)]

for _ in range(e):
    a, b, c = map(int, input().split())
    dist[a][b] = min(c, dist[a][b])

for k in range(1, v+1):
    for i in range(1, v+1):
        for j in range(1, v+1):
            if i != j:
                dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])

for i in range(1, v+1):
    for j in range(1, v+1):
        if dist[i][j] == 1e9:
            dist[i][j] = 0

# for i in range(1, v+1):
#     print(*dist[i][1:])

result = 1e9

for i in range(1, v+1):
    for j in range(1, v+1):
        if dist[i][j] != 0 and dist[j][i] != 0:
            result = min(result, dist[i][j] + dist[j][i])

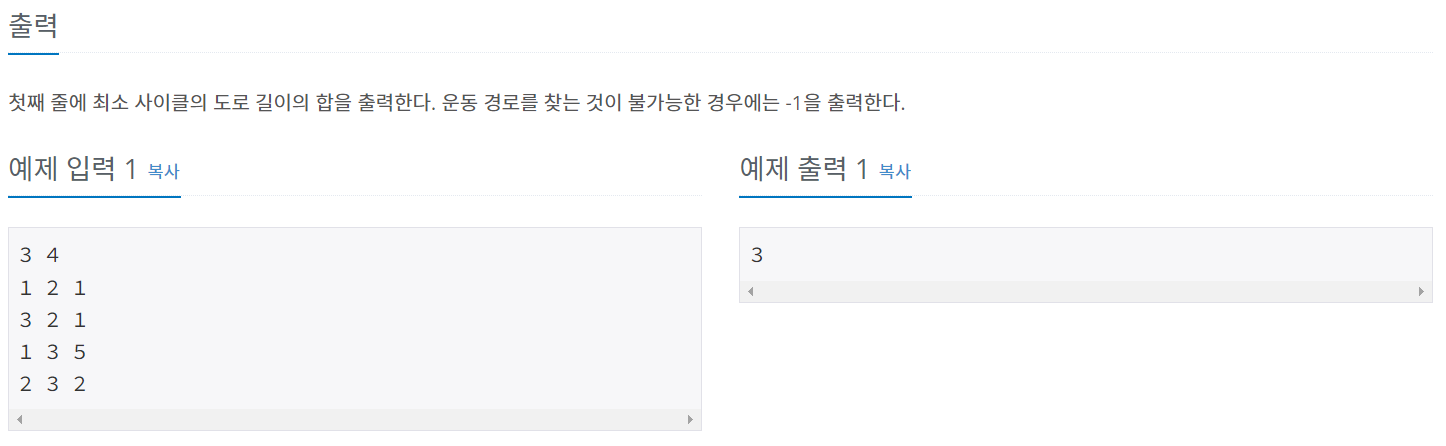
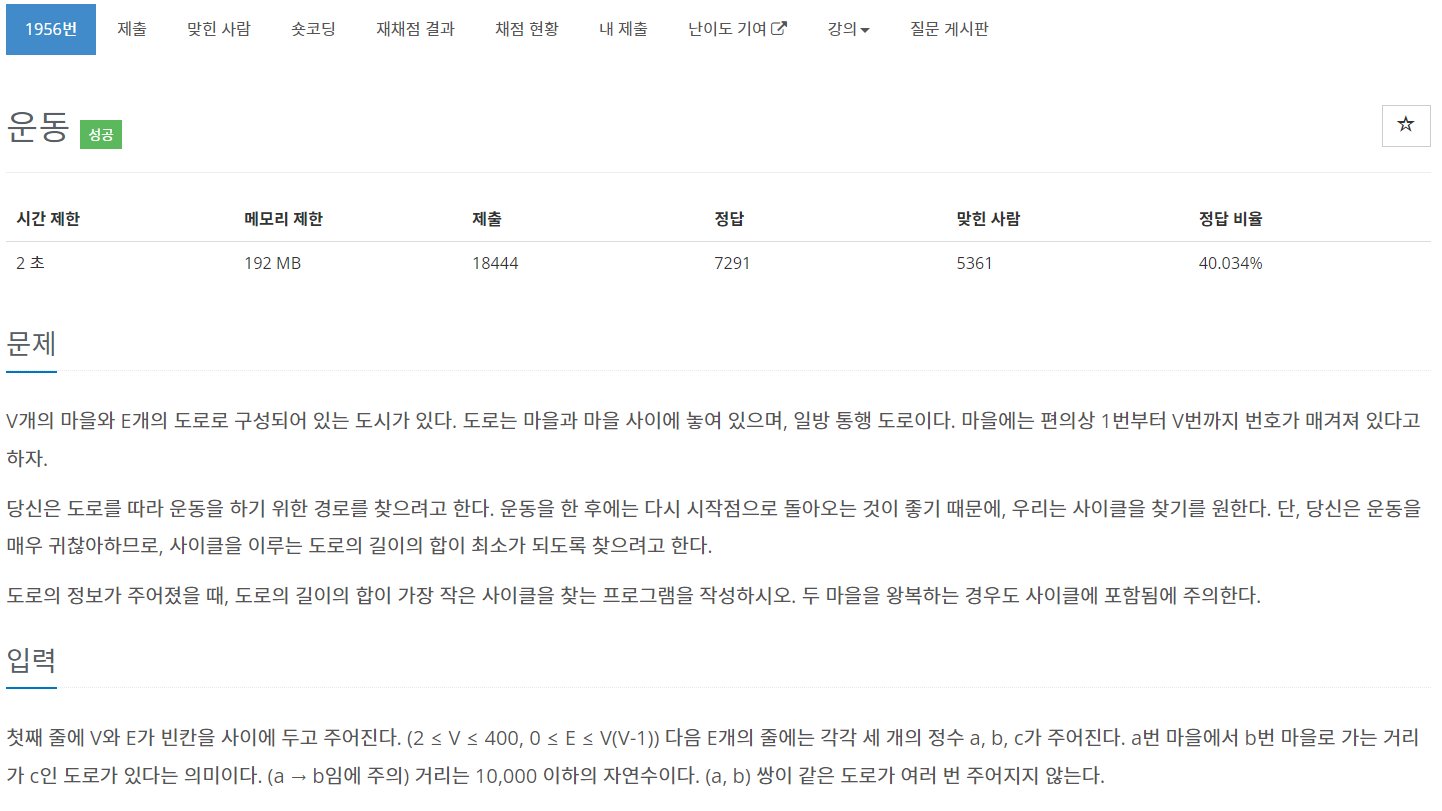
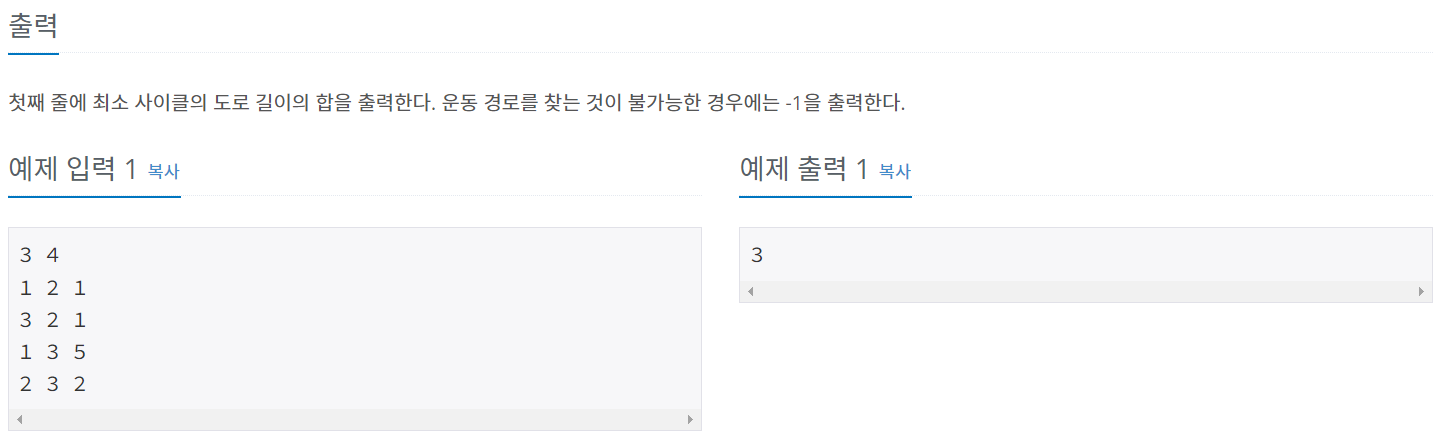
print(result if result != 1e9 else -1)

플로이드 와샬 알고리즘을 통해 해결할 수 있는 문제

이 문제는 최단 사이클을 구해야 한다. 즉 모든 노드에 대해서 최단 경로를 구한 후 그 중 사이클이 가능한지 여부와 최단 사이클을 구해야한다.

노드의 갯수가 적으므로 이 플로이드 와샬 알고리즘을 통해 모든 노드에서의 최단 경로를 우선 구한다.

그 후 사이클이 가능한 여부를 판단하는데
2중 for문을 돌면서 dist[i][j]가 0이 아닐때 dist[j][i]가 0이 아니면 해당 노드에서 출발해서 해당 노드로 돌아오는 최단거리 사이클이 존재한다는 뜻이된다.

그렇기 때문에 해당 조건일때의 최소값을 구해서 정답을 구할 수 있다.