
첫시도
def solution(gems):
def dfs(start, idx):
if idx == len(gems):
return [0, len(gems)]
for i in gem_dict:
if gem_dict[i] == 0:
break
else:
return [start, idx]
gem_dict[gems[idx]] += 1
return dfs(start, idx+1)
answer = [0,len(gems)]
gem = set(gems)
gem_dict = dict()
c_flag = False
for i in range(len(gems)-len(gem)):
for g in gem:
gem_dict[g] = 0
gem_dict[gems[i]] += 1
start, end = dfs(i, i+1)
start += 1
if answer[1] - answer[0] > end - start:
answer = [start, end]
return answer테스트 케이스는 넘어갔지만
제출에서 처참한 결과가 나왔다.

정확성도 맞지 않을 뿐더러 효율적이지도 않다고한다.....
gems 배열 크기가 최대 100,000 이므로 위 코드의 시간 복잡도인 nO(logn)으로 해결 가능하다고 생각했는데 히든 케이스는 더 큰 크기의 리스트가 주어지는 듯 하다.
def solution(gems):
gems = gems + [" "]
answer = [1,len(gems)]
l = len(set(gems))-1
gem_dict = dict()
start = end = 0
while start < len(gems) and end < len(gems):
if len(gem_dict) < l:
if gems[end] in gem_dict:
gem_dict[gems[end]] += 1
else:
gem_dict[gems[end]] = 1
end += 1
else:
if end - start < answer[1] - answer[0] + 1:
answer = [start+1, end]
gem_dict[gems[start]] -= 1
if gem_dict[gems[start]] == 0:
del gem_dict[gems[start]]
start += 1
return answer투 포인터 알고리즘으로 해결 가능한 문제
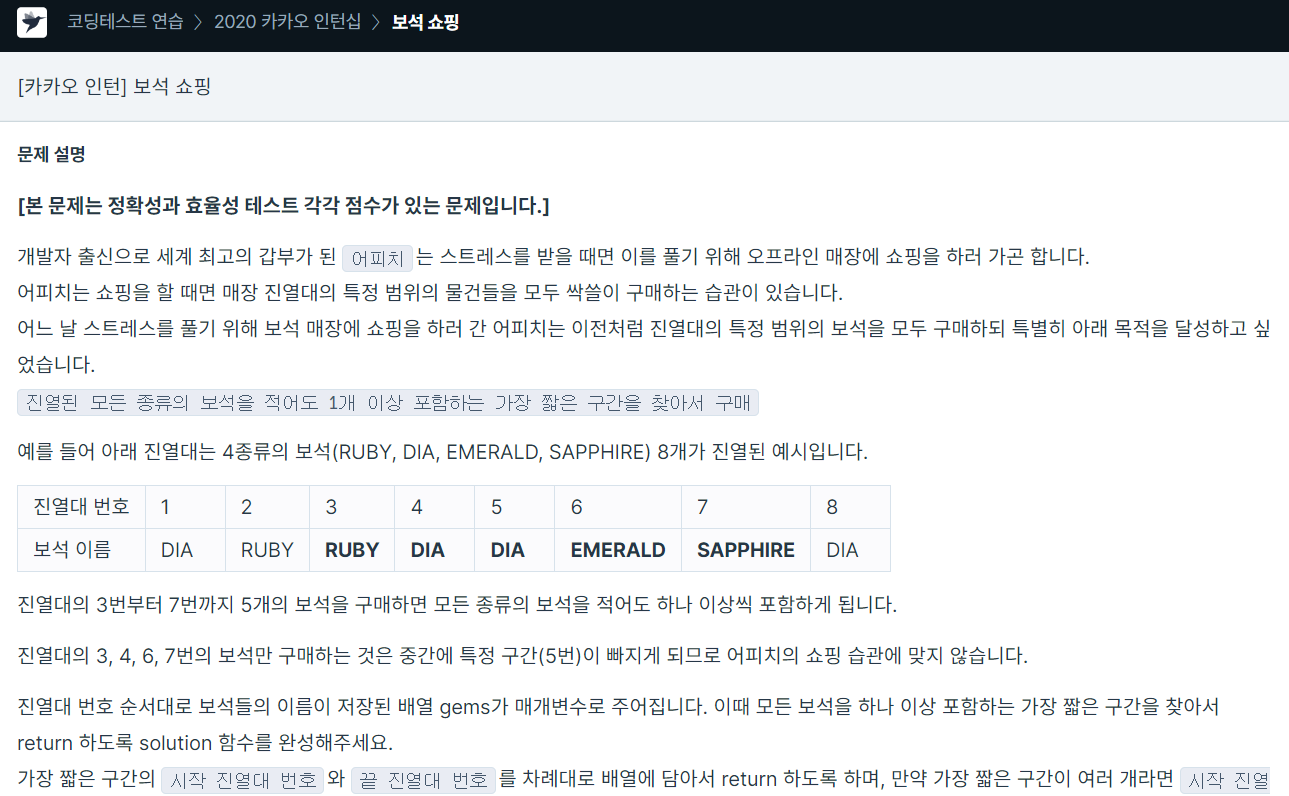
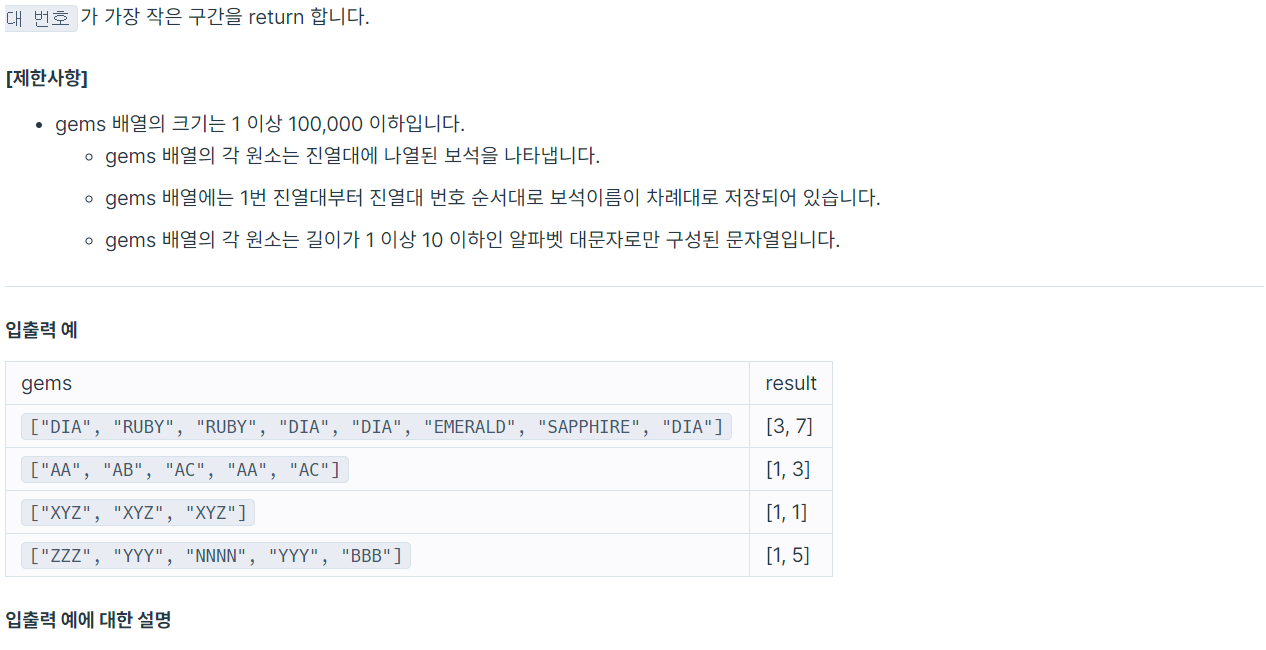
보석 정보를 딕셔너리에 저장한다. 딕셔너리의 크기가 보석의 수와 같아질 때까지 end를 1 씩 증가시킨다. 같아지면 딕셔너리 정보를 수정해나가면서 start를 1씩 증가시킨다.
백준에서 투 포인트 알고리즘을 공부 한 후 접한 문제지만 투 포인트 알고리즘을 적용시킬 생각을 전혀 하지 못했다.....
아직 경험이 많이 부족하다고 느낀 문제였다.
