프로그래머스 / 스티커 모으기(2) / python

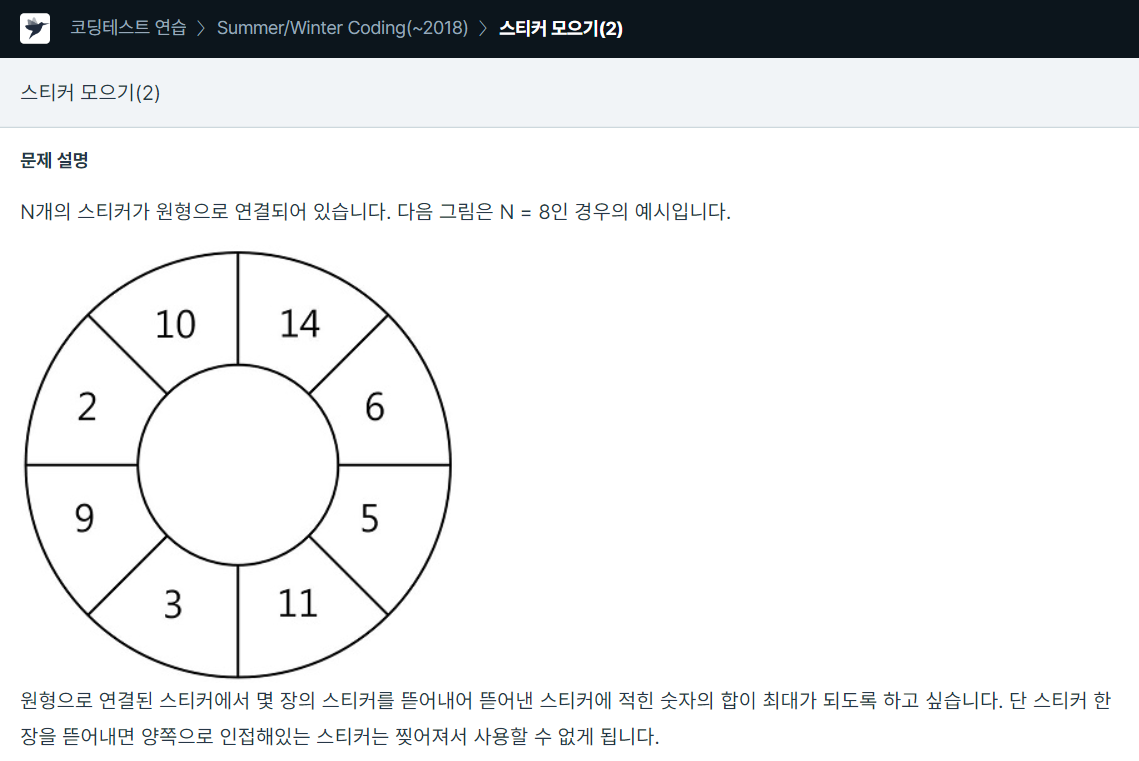
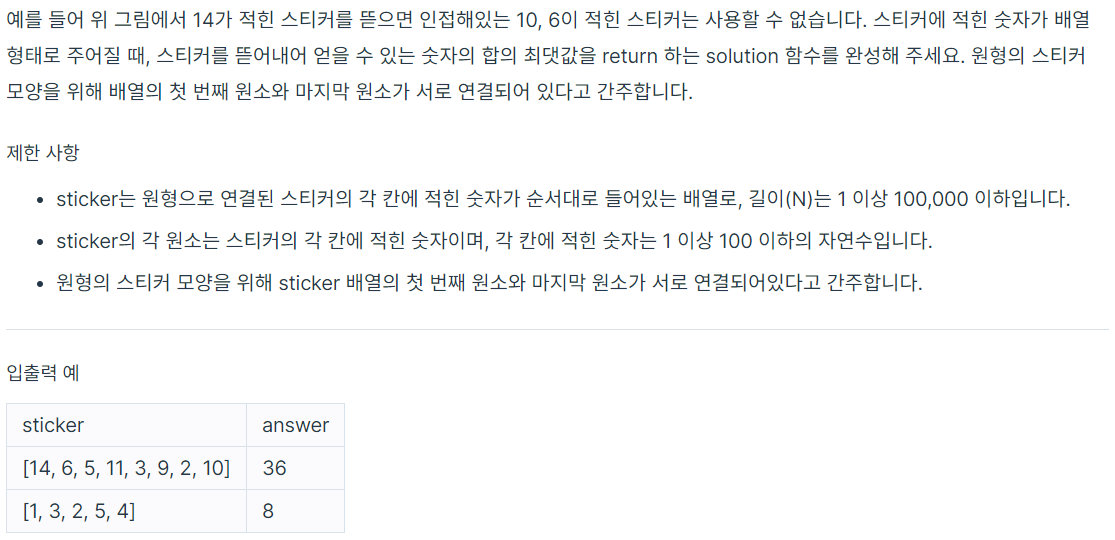
처음 시도 방법

import sys
sys.setrecursionlimit(10000)

answer = 0
def solution(sticker):
    global answer
    def dfs(idx, t):
        global answer
        if idx == len(sticker)-1:
            # print(visited)
            if visited[0] ==True or visited[idx-1] == True:
                answer = max(answer, t)
            else:
                answer = max(answer, t+sticker[idx])
            return
        
        # if dp[idx][t] != 0:
        #     return
        dp[idx][t] = 1
            
        if visited[idx-1] == False:
            visited[idx] = True
            dp[idx][t+sticker[idx]] = 1
            dfs(idx+1, t+sticker[idx])
        visited[idx] = False
        dfs(idx+1, t)
            
    dp = [[0] * sum(sticker) for _ in range(len(sticker))]
    visited = [False] * len(sticker)
    
    visited[0] = True
    dfs(1, sticker[0])
    visited = [False] * len(sticker)
    dfs(1, 0)
    
    return answer

dp와 bfs로 시도 했었다.
테스트 케이스에 대해서는 맞았지만 히든 케이스에 대해서는 처참한 결과였다. dp 점화식을 잘 작성하면 굳이 dfs 필요없이 그냥 현재 상태에서의 최대값만을 저장해 나갈 수 있어서 메모리와 시간 둘다 아낄 수 있다.

히든 케이스에 대해서 시간 초과와, 런타임 에러가 발생한 걸로 보아 주어지는 히든 케이스의 리스트 크기가 매우 큰것으로 보인다.

dp로 진행하는 방식으로 재시도

def solution(sticker):
    answer = 0
    l = len(sticker)
    if l == 1:
        return sticker[0]
    dp = [[0,0] for _ in range(l)]
    dp[0][0] = sticker[0]
    dp[1][0] = sticker[0]
    dp[1][1] = sticker[1]
    
    for i in range(2, l):
        dp[i][0] = max(dp[i-2][0] + sticker[i], dp[i-1][0])
        dp[i][1] = max(dp[i-2][1] + sticker[i], dp[i-1][1])

    return max(dp[-1][1], dp[-2][0])

dp[i][0]은 첫 스티커를 땐 경우이고
dp[i][1]은 첫 스티커를 때지 않고 두 번째 스티커를 땐 경우이다.

첫 스티커를 땠으면 마지막 스티커에 대한 정보를 무시해야하므로 마지막에 첫 스티커를 땐 경우는 dp의 마지막 정보가 아니라 마지막에서 두번째 정보를 비교해줘서 정답을 구한다.

---

간단한 문제도 어렵게 생각하는 경향히 있다....
알고나서 간단하게 보이는건가.. 확실한건 문제 경험이 더 필요해 보인다.