이 정렬은 효율적일 수도 있고 아닐 수도 있습니다, 퀵 정렬(Quick Sort)에서 이어집니다.
점차 진화한 정렬에 관해서 이야기하는 흐름을 따라가면 퀵 정렬 이후의 이야기를 해야할 것 같지만, 이번에는 사실 퀵 정렬 이전에 나온 정렬을 이야기할 것이다. 컴퓨터 과학의 천재 존 폰 노이만(워드프로세서 자격증 따 보신분들은 다 들어본 그 분)이 만든 머지 정렬이다. 사실 퀵 정렬이 나중에 나온 만큼, 대부분의 경우에 머지정렬보다 퀵 정렬이 높은 효율을 보인다. 그렇지만 퀵 정렬은 그럴 수도 있고 아닐 수도 있는 알고리즘이다. 감독으로서 홈런 타자를 데리고 있는 것도 중요하지만, 시즌 구상에 앞서 매해 3할에 100안타 이상을 보장하는 내구성 좋은 타자가 많은 것 역시 중요하다. 대비하는 자, 개발자 역시 마찬가지로 성능이 일정한 정렬을 필요로 할 때가 있는 것이다.
머지정렬
머지 정렬은 병합정렬이라고 번역해서도 불린다. 병합한다라는 말은 하나의 배열을 정렬하는 함수에게 그다지 어울리는 말이 아닌 것 같다. 그렇기에 병합하는 함수는 닭가슴살을 찢거나 티모를 찢는 것처럼, 배열을 야무지게 쪼개는 함수와 짝을 이루어 머지정렬을 수행한다.
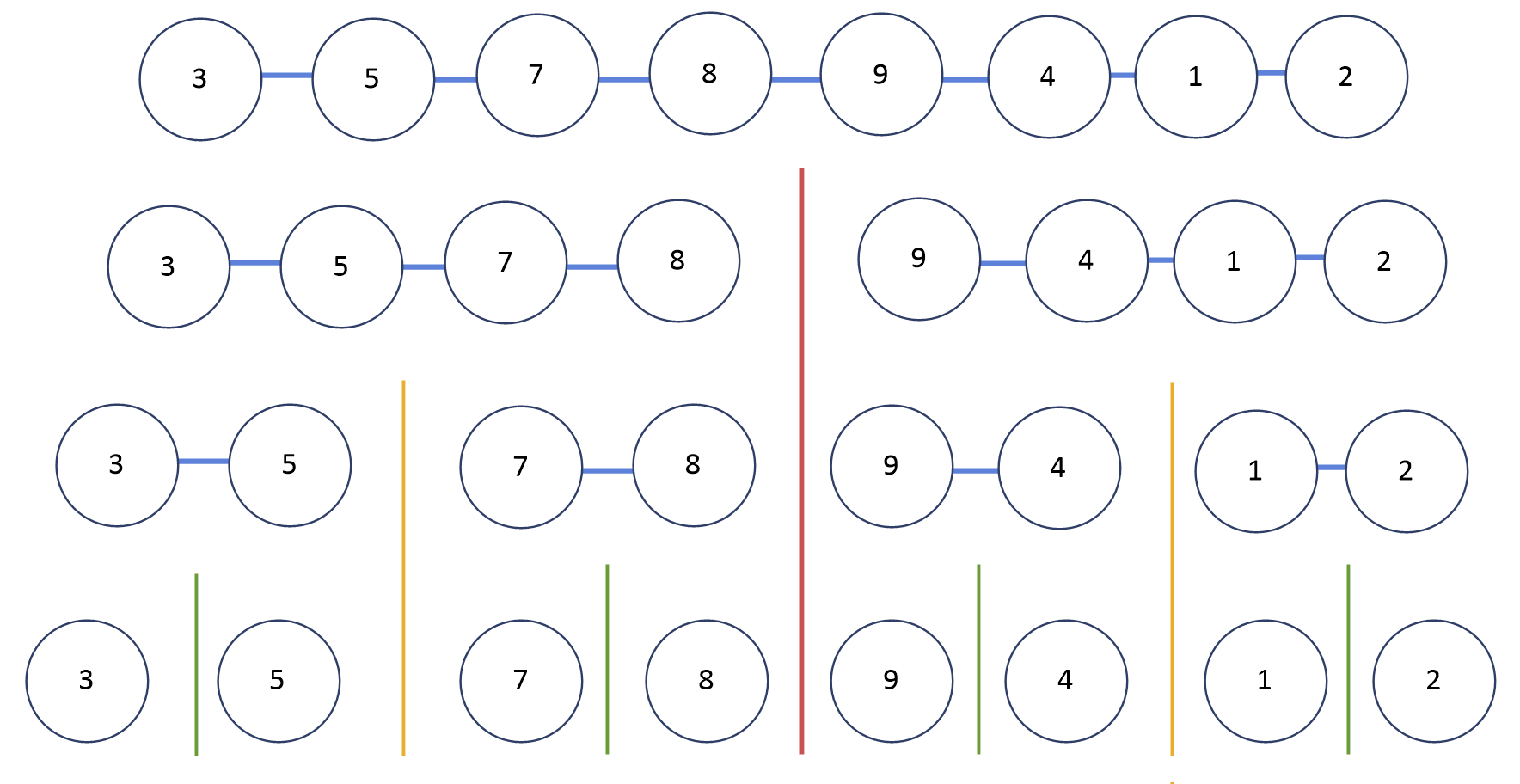
그림과 같이 배열을 전부 나눈다. 당연스레 2분한 것처럼 보이지만, 가장 직관적이면서 충분히 효율적이기도 하다. 나눌 때는 보편적으로 재귀형태의 함수 호출을 활용한다.
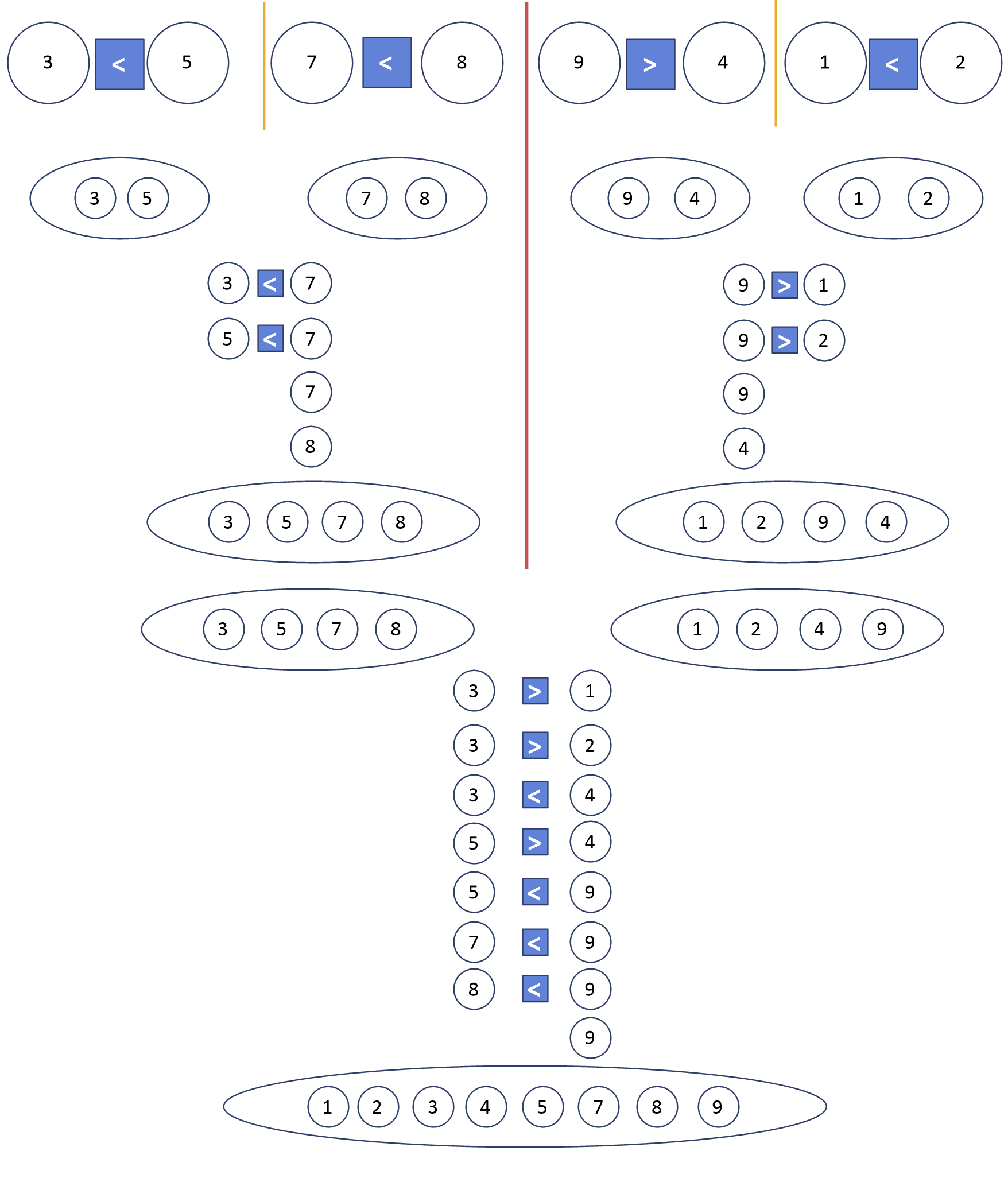
병합할 때의 핵심은 각 배열의 요소를 하나씩 꺼내 서로 비교하는 것이다. 해당 그림에서는 오름차순 정렬이므로, 작은 수를 먼저 넣어준다.
머지정렬의 구현
파이썬으로 머지정렬을 구현하고 원리를 이야기해보자.
병합함수
# 병합함수 선언
def merge(arr1, arr2):
# 결과 반환할 배열 선언
result = []
# 두 배열의 포인터 선언 및 초기화
i = j = 0
# i와 j가 각 배열 안의 인덱스를 가리키고 있으면 반복
while i < len(arr1) and j < len(arr2):
# 만약 i가 가리키는 값이 j가 가리키는 값보다 작으면
# i가 가리키는 값을 result에 넣고 i값 +1
if arr1[i] < arr2[j]:
result.append(arr1[i])
i += 1
# 만약 j가 가리키는 값이 i가 가리키는 값보다 작으면
# j가 가리키는 값을 result에 넣고 j값 +1
else :
result.append(arr2[j])
j += 1
# 위의 반복문을 통과했으면, i 혹은 j가 가리키는 배열을 벗어난 상태
# i가 벗어난 것이 아니라면
while i < len(arr1):
# i가 가리키는 값을 순서대로 result에 넣고 i값 +1
result.append(arr1[i])
i += 1
# j가 벗어난 것이 아니라면
while j < len(arr2):
# j가 가리키는 값을 순서대로 result에 넣고 j값 +1
result.append(arr2[j])
j += 1
return result앞서 말한 것과 마찬가지로 배열을 병합하는 함수와 배열을 분할하는 함수를 나누어 구현하였다. 병합하는 함수는 나뉜 배열 중 두 개를 인자로 받아, 순서를 비교한 후 정렬된 배열로 차례로 넣는 연산을 한다.
분할함수
# 머지 정렬함수 선언, 머지함수를 호출하기 전 까지, 분할하는 역할을 수행함
def mergesort(lst):
# 만약 배열의 길이가 1보다 작으면, 인자로 받은 배열을 바로 반환
if len(lst) <= 1:
return lst
# 배열의 중간 인덱스값 저장
mid = len(lst)//2
L = lst[:mid]
R = lst[mid:]
# 병합함수 호출, 동시에 인자 값으로 머지 소트함수 재귀 호출
# 머지 소트 함수는 머지 함수 혹은 길이 1짜리 배열을 반환하고, 머지함수는 정렬된 배열을 반환
return merge(mergesort(L), mergesort(R))
머지 정렬함수는 재귀 형태로 머지 정렬함수를 호출하며, 호출한 머지 함수를 인자로 하는 머지함수(병합함수)를 호출한다. 배열 [3, 5, 7, 8, 9, 4, 1, 2]를 오름차순 머지정렬하면 다음과 같이 함수 호출이 진행된다.
#1. mergesort([3, 5, 7, 8, 9, 4, 1, 2])
# 2. merge(
mergesort([3, 5, 7, 8]),
mergesort([9, 4, 1, 2])
)
# 3. merge(
merge(
mergesort([3, 5]),
mergesort([7, 8])),
merge(
mergesort([9, 4]),
mergesort([1, 2])
)
)
4. merge(
merge(
merge(
mergesort[3],
mergesort[5]
),
merge(
mergesort[7],
mergesort[8]
)
),
merge(
merge(
mergesort[9],
mergesort[4],
),
merge(
mergesort[1],
mergesort[2]
),
),
)
5. merge(
merge(
merge([3], [5]),
merge([7], [8])
),
merge(
merge([9], [4]),
merge([1], [2]),
),
)
6. merge(
merge([3, 5], [7, 8]),
merge([4, 9], [1, 2])
)
7. merge([3,5,7,8], [1,2,4,9])
8.[1,2,3,4,5,7,8,9]머지정렬의 시간복잡도
머지정렬은 완전이진트리처럼 배열을 분할하는 함수는 복잡한 연산이 있지 않다. 배열의 len값을 호출하는 정도와 재귀호출하는 정도가 그나마 복잡한 수준이다. 시간 복잡도의 열쇠는 병합하는 함수에 있다. 병합하는 함수는 완전이진트리의 형태로 생각하면 h = log2(N-1)이므로 높이마다의 연산을 log2(N-1)번 하면 된다. 높이마다의 연산은 두 배열의 모든 요소를 한 번씩 순회하는 시간복잡도 O(n)의 연산이므로 총 시간복잡도는 O(n log n)이 된다.
앞서 말했듯 이 시간복잡도는 배열의 형태에 관계 없이 일정한 복잡도를 띄므로, 유용하게 사용되는 정렬이다. 팀정렬이라는 최적화 정렬알고리즘에도 머지정렬과 삽입정렬이 기초로 사용되었다.
