정렬은 가장 직관적인 알고리즘 종류 중 하나다. 초등학교에 들어가자마자 하는 "키 순으로 서세요"는 정렬 중에서도 아주 실용적인 정렬이다. 그렇지만, 키 순으로 서면서 자기 자리를 여러번 움직여 본 분들은 아시겠지만, 나의 위치를 정확히 알지 못하는 상태에서 지시어 "키 순으로 서라"는 것은 매우 번거로운 작업이다. 마찬가지로, 효율에 영혼도 팔 수 있을 것 같은 분들은, 오름차순과 내림차순을 곧이 곧대로 비교하여 정렬하는 자신을 용납할 수 없었던 것 같다.
버블정렬
알고리즘을 조금 공부해보면 배우는 것이 하나 있다.
버블정렬만 떠오르면 망한것이다.
도대체 왜 이런 취급을 받을까.
버블정렬은 서로 인접한 두 원소를 비교하여, 순서에 맞지 않으면 교환하는 정렬형태다. 일상에서 보면 경민이, 민수, 정훈이, 원호, 수환이가 순서대로 서 있을 때, 계속 맨 앞에 있는 친구부터 자를 들고 키를 비교하는 모양세다. 줄의 뒤쪽에 키가 가장 크다고 확정되면, 자를 맨 앞에 친구에게 넘겨주고, 줄이 다 맞춰질 때까지 기다리는 모습과 유사하다.
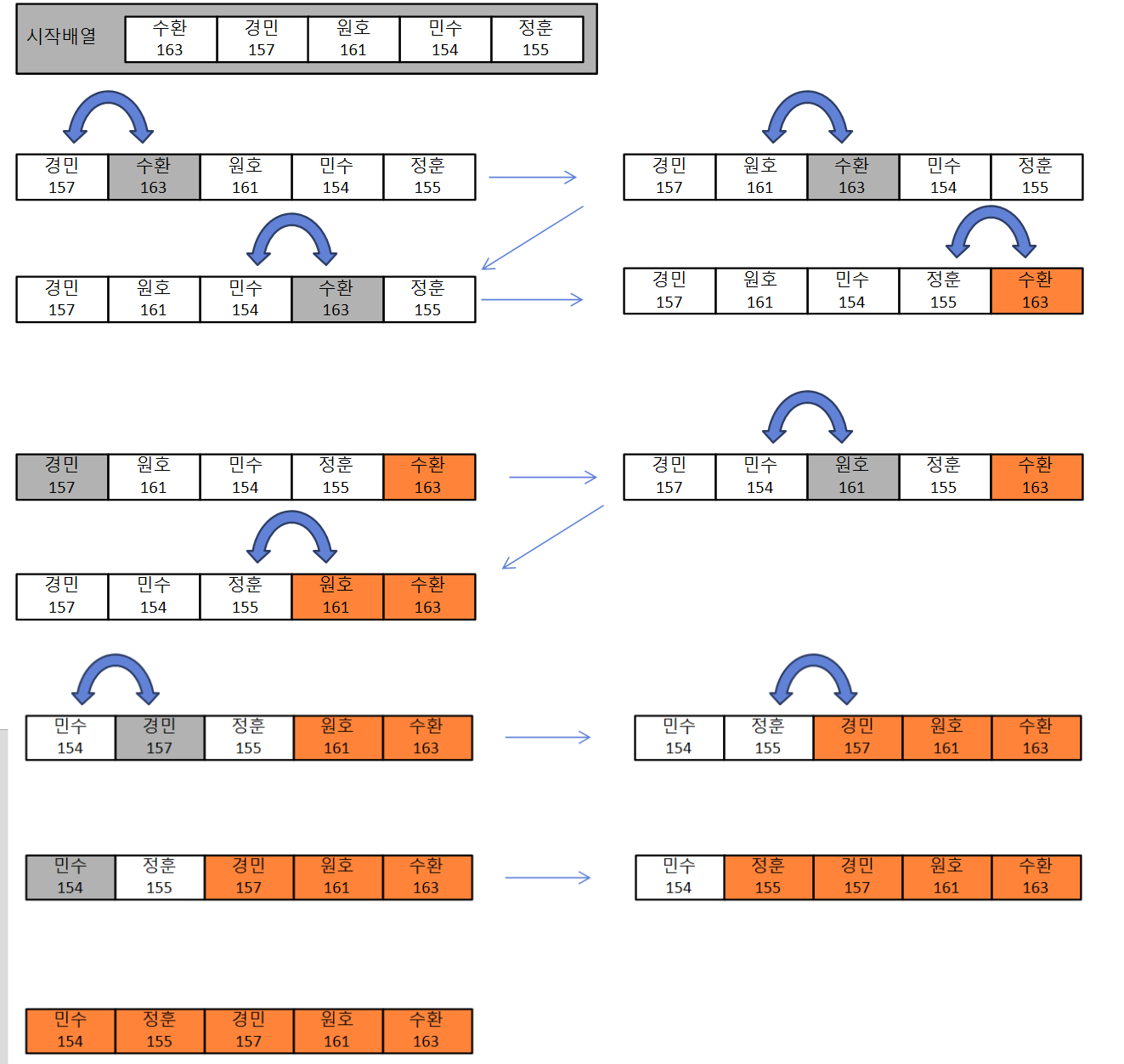
어느 학교의 선생님이 이런 식으로 줄을 세운다고 하면, 옆 반 선생님은 의아하게 쳐다볼 것이고, 학생들의 불만도 만만치 않을 것이다. 그 만큼 많은 비교연산이 일어나고, 시간이 걸리는 정렬이다. 하지만, 모든 정렬은 버블정렬에서 나온다고 할 수 있다. 버블정렬에서 어떤 부분을 생략할 수 있을까를 고민한 모습이라 할 수 있다.
버블정렬의 구현
# 오름차순 버블소트 선언
def bubblesort(lst):
# 정렬할 요소 수 저장
iters = len(lst)-1
# 모든 요소가 정렬될 때까지 반복
# 한번 순회할 때마다, 가장 높은 값이 하나씩 정해지기 때문에, 비교하는 원소의 수가 하나씩 줄어듦.
for iter in range(iters):
# 가장 높은 순으로 정렬된 값들을 제외한 배열의 길이를 wall에 저장
wall = iters - iter
# 현재 비교를 진행하는 값이 비교해야 하는 횟수를 채우기 전까지 반복
for cur in range(wall):
# 만약 비교하는 값이 비교당하는 값보다 크다면
if lst[cur] > lst[cur+1]:
# 둘의 위치를 교환
lst[cur], lst[cur+1] = lst[cur+1], lst[cur]
# 정렬된 배열 반환
return lst버블정렬도 얼핏보면 헷갈리곤 한다. cur은 자를 들고 움직이는 친구, cur+1은 그 친구와 키를 비교당하는 친구, wall은 아직 자기 순서가 어디인지 모르는 친구들의 수라고 생각하면 조금 더 직관적이다.
선택정렬
우리가 학교에서 가장 많이 하는 정렬형태는 선택정렬에 가깝다. 선택정렬을 진행할 때 나오는 소리는 다음과 같다.
"야, 너 키 크니까 뒤에 쟤랑 바꿔"
"너 제일 작으니까 맨 앞에 애랑 바꿔야겠다!"
정렬 기준에 끝단에 부합하는 요소를 찾아 위치를 확정시키는 방식이 선택정렬이다. 우리나라의 선생님들이 훌륭한 교육자임을 증명하는 가장 쉬운 방법은 배우지 않아도 선택정렬을 자유자재로 구사하는 모습을 보여주는 것이다. 심지어, 선택정렬을 연속적으로 시행하거나, 제일 큰 값과 작은 값을 동시에 정렬하는 모습도 볼 수 있다.
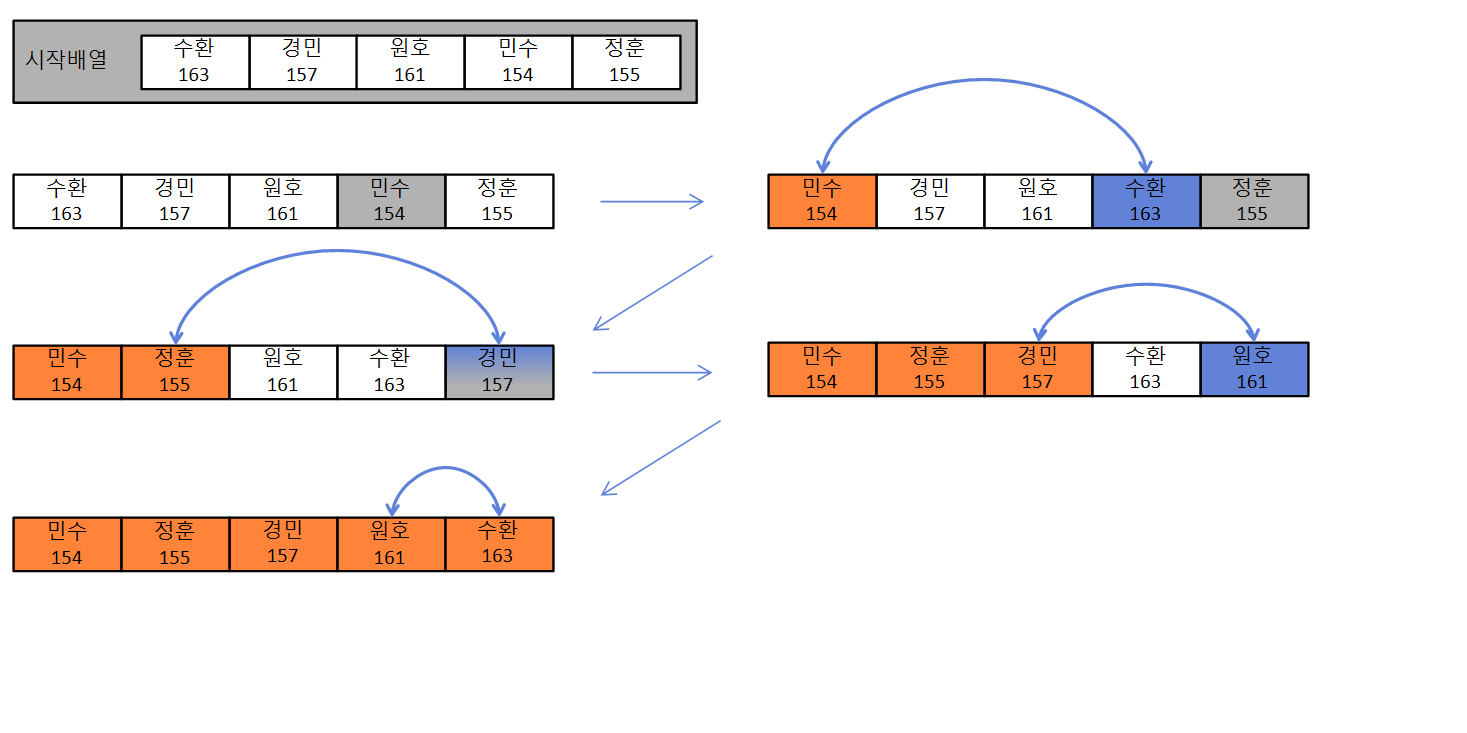
얼핏보더라도, 움직이는 횟수가 확연이 줄어들었다. 일일이 비교하는 과정을 최대값을 찾는 과정을 통해 확연히 줄인 것처럼 보인다. 이것은 키로 줄을 세울 때는 가능한 방법이지만 사실 코드로 구현할 때는 결국 반복적인 비교가 필요하다.(사실 키로 줄을 세울 때도, 직관이라는 놀라운 프로그램이 순간 연산을 진행해준다.) 다만, 비교적 좋은 효율을 기대할 수 있는 점은, 순서를 바꾸는 비용을 아낀다는 점이다.
선택정렬의 구현
# 오름차순 선택정렬 선언
def selectionsort(lst):
# 정렬할 요소 수 저장
iters = len(lst)-1
# 반복마다 가장 작은 값이 정해지기 때문에, 비교할 요소 수가 줄어듦.
for iter in range(iters):
# 비교할 요소들 중 가장 앞의 인덱스 값을 minimum에 저장
minimum = iter
# minimum이 가리키는 값과 뒤의 요소들을 차례로 비교
for cur in range(iter+1, len(lst)):
if lst[cur] < lst[minimum]:
# minimum이 가리키는 값보다 작은 값이 있으면, 그 값의 인덱스로 minimum 갱신
minimum = cur
# 만약 minimum에 담긴 인덱스가 가장 앞의 인덱스가 아니라면
if minimum != iter:
# 미니멈의 값과 비교하는 요소들 중 맨 앞의 값을 교체
lst[minimum], lst[iter] = lst[iter], lst[minimum]
# 정렬된 배열 반환
return lst정말 아쉽게도, 줄을 설 때는 가장 큰 친구만 움직이거나, 가장 작은 친구만 앞으로 움직이면서 나머지 친구들은 '눈치껏' 간격을 재조정한다. 자료구조에서는 그 재배치가 전부 비용이기 때문에 1대1 교환 방식을 선택했다. 왜냐하면, 우리가 얻고자 하는 값을 제외한 나머지의 무질서는 고려 대상이 아니기 때문이다.
삽입정렬
삽입정렬은 오늘 볼 정렬 중에 가장 현실적이다. 무질서함이 널부러져 있으면, 그 무질서 중에서 질서에 맞는 값들을 정리 하면서 동시에 공간을 만들기 위해 무질서한 값들을 정리할 필요도 있다. 때문에 무질서한 것들을 한쪽 구석으로 치워놓고, 하나씩 질서에 맞춰 세워놓는 것은 내가 가장 많이하는 방 정리 방법이다.
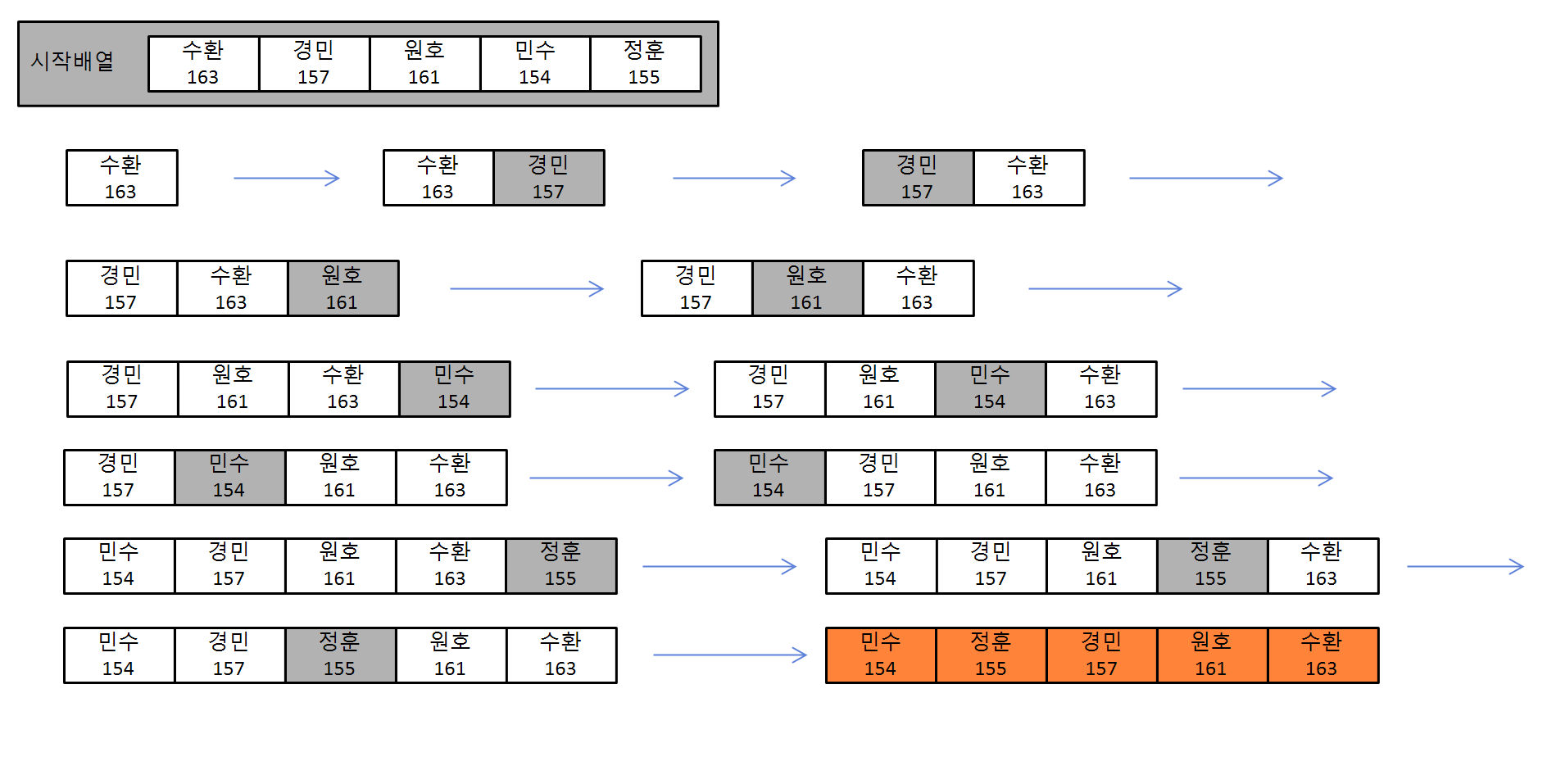
하나의 요소로 시작한 배열이 점차 시작배열과 같은 요소 수를 갖는 형태다. 각 순회마다 비교를 하는 주체 요소가 정해진 것이 버블정렬과 유사한 형태이다. 하지만, 한번 순회마다 비교하는 요소의 수가 버블정렬에 비해 적은 것이 특징이다.
삽입정렬의 구현
# 오름차순 삽입정렬 선언
def insertionsort(lst):
# 배열을 순회
for cur in range(1, len(lst)):
# 삽입배열을 순회
for delta in range(1, cur+1):
# 삽입배열에 삽입한 요소(비교할 요소)의 인덱스 값 cmp에 저장
cmp = cur-delta
# 만약 삽입한 요소가 비교당하는 요소보다 크면, 두 요소의 값을 교환
if lst[cmp] > lst[cmp+1]:
lst[cmp], lst[cmp+1] = lst[cmp+1], lst[cmp]
# 삽입한 요소가 비교당하는 요소보다 작으면, 반복문 종료하고 저장
else:
break
# 정렬된 배열 반환
return lst
# 오름차순 삽입정렬2 선언
def insertionsort2(lst):
# 배열의 요소 순회
for idx in range(1, len(lst)):
# 삽입하는 요소의 값 val에 저장
val = lst[idx]
# 비교하는 요소의 인덱스 값 cmp에 저장
cmp = idx-1
# 비교하는 요소의 크기가 삽입한 요소의 값보다 크고,
# 비교하는 요소의 인덱스가 0 이상일 때
while lst[cmp] > val and cmp >= 0:
# 교체할 인덱스의 값을 cmp+1에 미리 저장
lst[cmp+1] = lst[cmp]
# 비교하는 요소 인덱스 조정
cmp -=1
# 반복문이 끝나면 삽입한 요소의 인덱스 확정
lst[cmp+1] = val삽입 정렬은 모두 빠져있다가, 한 사람씩 줄을 서는 상황과 같다. 들어가는 사람은 맨 앞에서 한 사람씩 비교해서 자기 순서를 찾는 정렬이다. 때문에, 비교하는 요소 수가 버블정렬에 비해 적다. 그리고 인덱스 값을 활용하여 순서 교환을 계산한다.
