[딥러닝 2단계] 7. 다중 클래스 분류

1. Softmax Regression

softmax regression

• 로지스틱 회귀를 일반화
• 여러 클래스 예측에 사용

Recognizing cats, dogs, and baby chicks

• C=class의 개수=4개
  • 고양이: 클래스 1, 개: 클래스 2, 병아리: 클래스 3, 해당 x: 클래스 0
    

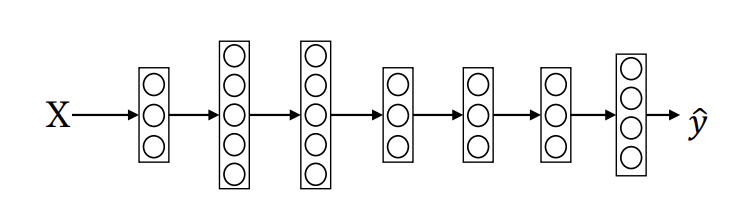
• n^[L]=4=C
  • 첫번째 단위=P(other|x)=입력값 x가 주어졌을 때 기타 클래스가 나올 확률
  • 두번째=P(cat|x)
  • 두번째=P(dog|x)
  • 네번째=P(병아리|x)
• 출력값 ŷ=(4,1)차원 벡터
• ŷ 각 값들의 합=1

Softmax layer

Activation function

• 입력값과 출력값이 모두 벡터

$t=e^{z^{[L]}}$
$a^{[L]}=e^{z^{[L]}}/\sum_{j=1}^{4} t_i$
$a_i^{[L]}=t_i/\sum_{j=1}^{4} t_i$

예시

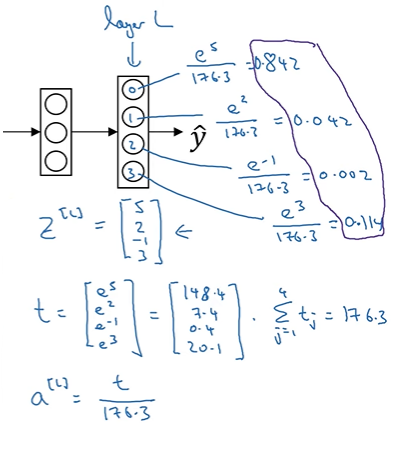
클래스 0,1,2,3이 될 확률 구하기

Softmax examples

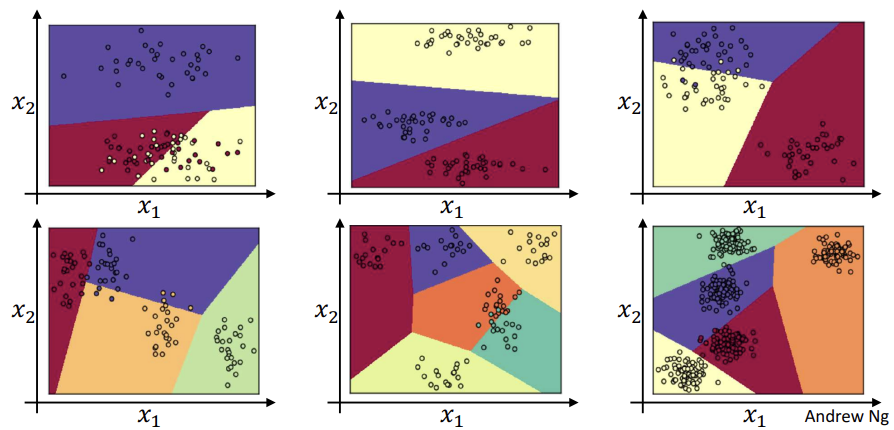
• 두 클래스 사이의 경계가 선형
• 만약 은닉 유닛이 여러 개인, 더 깊은 신경망을 다룬다면 여러 클래스를 분류하기 위해 더 복잡하고 비선형의 경계도 볼 수 있을 것

2. Softmax 분류기 훈련시키기

Understanding softmax

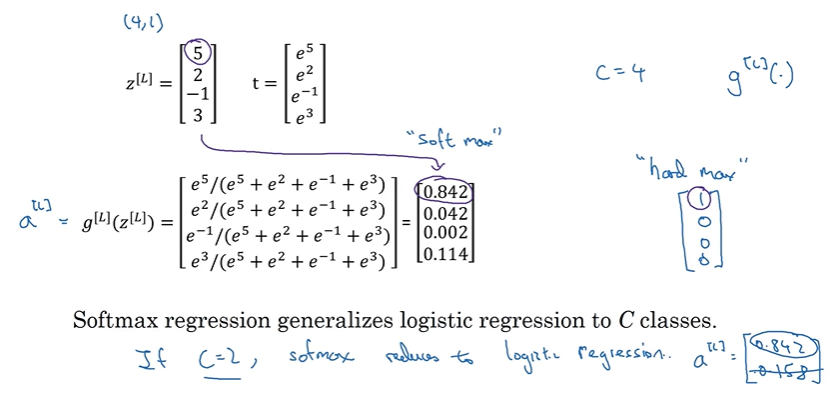
• hardmax: z의 원소를 살펴보고 가장 큰 값이 있는 곳에 1을 나머지에는 0을 갖는 벡터로 대응시키는 것
• softmax: z를 확률들로 대응시키는 것

• 소프트맥스 회귀나 활성화 함수는 두 클래스만 다루는 로지스틱 회귀를 일반화한 것이다.
  • C=2 -> 로지스틱 회귀와 동일

Loss function

하나의 훈련 샘플

• y=[0 1 0 0], ŷ=[0.3 0.2 0.1 0.4]

$L(ŷ,y)=-\sum_{j=1}^{4}y_jlogŷ_j$

-> $-y_2logŷ_2=-logŷ_2$

• L을 작게 만들기 위해선 ŷ_2을 크게 만들어야함
• 입력값 x에 대응하는 출력값의 확률을 키워주는 것

전체 훈련 세트

$J(w^{[1]},b^{[1]},...)=1/m\sum_{i=1}^{m}L(ŷ^{(i)},y^{(i)})$
Y=[y^(1) y^(2),..., y^(m)]

Gradient descent with softmax

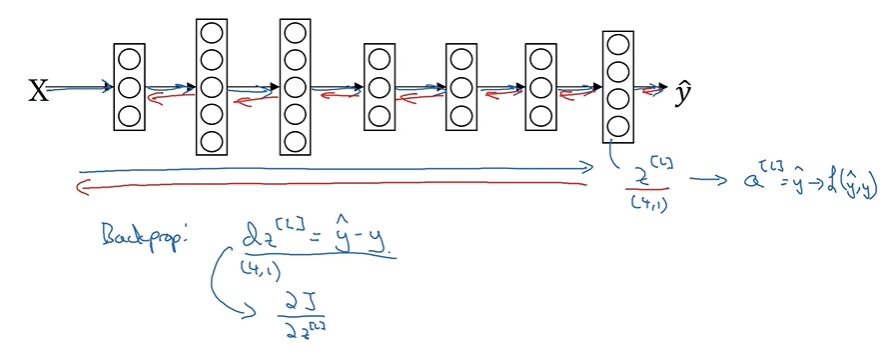
• Softmax 와 손실함수를 결합한 역전파의 값 dz^[L]은 z^[L]에 대해 편미분한 것

---

해당글은 부스트코스의 [딥러닝 2단계] 7. 다중 클래스 분류 강의를 듣고 작성한 글입니다.