
자료구조와 알고리즘
자료구조(Data structure)
- 자료 값의 모임, 자료 간의 관계, 자료에 적용할 수 있는 함수나 명령
- 만능인 자료구조는 없으며, 상황에 맞는 자료 구조를 사용해야 함
- 자료: 현실 세계로부터 수집한 사실이나 개념의 값 또는 이들의 집합
-> 정보: 자료를 특정 용도로 사용하기 위해 처리/가공한 것
추상자료형(Abstract data type)
- 추상자료형은 자료구조와 유사하지만, 구체적인 구현 방법은 정의되어 있지 않음
- 자료구조를 구현할 때에는 자료구조 자체를 자세히 알아야 하지만, 자료구조를 활용하기 위해서는 추상자료형만 알아도 됨
- OOP 관점에서 보면 추상자료형은 추상 클래스 역할을 함
자료구조의 분류
-
선형 자료구조(Linear data structure)
-> 배열 (Array)
-> 리스트 (List)
-> 스택 (Stack)
-> 큐 (Queue)
-> 해시 셋 (Hash set)
-> 해시 테이블 (Hash table) -
비선형 자료구조(Nonlinear data structure)
-> 트리 (Tree)
-> 그래프 (Graph)
-> 힙 (Heap, Priority queue)
-> 트라이 (Trie: Retrieval tree)
자료구조의 필요성
- 필요한 자료에 효율적으로 빠르게 접근할 수 있게 함
- 저장장치를 효율적으로 사용할 수 있게 함
- 자료구조 별로 적절한 알고리즘을 기계적으로 적용할 수 있음
- 동료들과 협업하는 데 큰 도움이 됨
알고리즘(Algorithm)
- 어떤 문제 해결을 위한 절차나 방법
- 조건
-> 입력 (Input)
-> 출력 (Output)
-> 명확성 (Definiteness)
-> 유한성 (Finiteness)
-> 효과성 (Effectiveness)
알고리즘의 분류
- 정렬 (Sorting)
- 이진 탐색 (Binary search)
- 투 포인터 (Two pointers)
- 탐욕법 (Greedy)
- 분할 정복 (Divide & conquer)
- 동적계획법 (Dynamic programming)
- 백트래킹 (Backtracking)
- 최단 경로 (Minimum distance path)
- 최소 신장 트리 (Minimum spanning tree)
알고리즘의 복잡도
복잡도(Complexity)
- 알고리즘의 성능을 나타내는 척도
- 시간 복잡도 (Time complexity)
-> 알고리즘을 동작하는 데에 필요한 연산의 횟수 - 공간 복잡도 (Space complexity)
-> 알고리즘의 동작에 필요한 메모리의 크기 - 일반적으로 시간 복잡도와 공간 복잡도는 trade-off 관계가 있음
시간 복잡도(Time complexity)
- 계산 복잡도 (Computational complexity) 라고도 부르며, 알고리즘의 동작에 필요한 연산의 횟수
-> 연산은 기초 연산(elementary operation)을 의미 - 시간 복잡도가 낮을 수록 알고리즘의 성능이 좋음
공간 복잡도(Space complexity)
- 알고리즘의 동작에 필요한 메모리(RAM)의 크기
- 일반적으로 알고리즘이 동작하기 위해 필요한 메머리의 최대치(Peak memory)를 공간 복잡도라고 함
복잡도의 점진적 표기법
복잡도의 비교
- 절대적으로 성능이 더 좋은 알고리즘이 있을까?
- 복잡도를 비교할 때 단위는 어떻게 정할 것인가?
- 알고리즘 복잡도 비교의 어려운 점
-> 시간 복잡도 vs. 공간 복잡도 trade-off
-> 자료의 크기에 따른 복잡도의 차이
-> 자료의 내용에 따른 복잡도의 차이
복잡도의 분류
- 알고리즘 동작 상황에 따라 구분: 최악/최선/평균적인 경우
- 일반적으로 최악의 경우에 대해 알고리즘 복잡도 정의
최악의 경우 vs. 최선의 경우
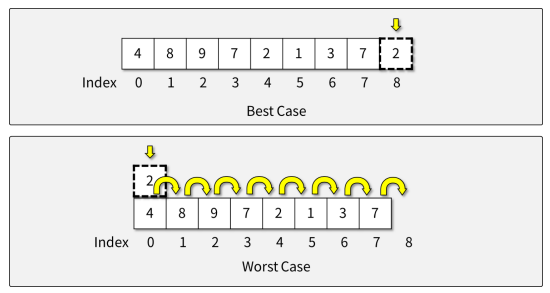
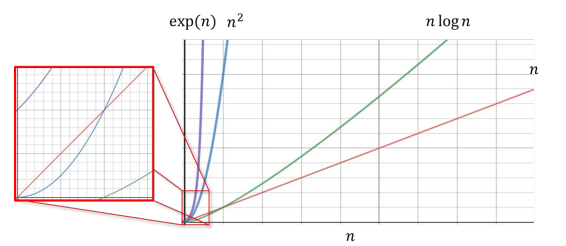
점진적 표기법
- 알고리즘에 입력되는 자료의 개수가 충분히 많다고 가정
- 성능 평가에 공평한 비교를 하기 위해 사용
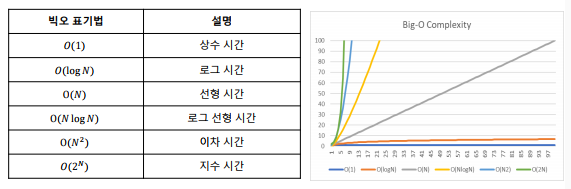
빅오 표기법(Big-O Notation)
- 충분히 큰 N에서 가장 큰 영향력을 주는 항을 기준으로 표기법 결정
이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다