통계 (6)

Chapter 2 기초통계-심화과정

분산 분석(ANOVA)

• 셋 이상의 모집단으로부터 추출한 양적 데이터를 비교하는 통계적 분석 방법
• t-test: 두개의 모집단의 평균 차이를 검정

분산분석의 이해

• 실험계획법(experimental design): 모집단의 특성에 대하여 추론하기 위해 특별한 목적성을 가지고 데이터를 수집하기 위한 실험 설계

• 반응변수: 관심의 대상이 되는 변수

• 요인/인자(Factor): 실험 환경 또는 조건을 구분하는 변수로 실험에 영향을 주는 변수

• 인자수준: 인자가 취하는 개별 값(처리:treatment)

• 모집단의 평균들을 비교하기 위하여 특성값의 분산 또는 변동을 분석하는 방법

• 실험을 통해 얻은 편차의 제곱합을 통해 평균의 차이를 검정

• 분산분석의 기본 가정
  1) 각 모집단은 정규 분포를 따른다
  2) 각 모집단은 동일한 분산을 갖는다
  3) 각 표본은 독립적으로 추출되었다

분산분석의 가설과 실험의 가정

• 가설
  -> $H_0$ : 각 집단의 평균은 동일하다 vs $H_1$: 각 집단의 평균에 차이가 있다

• 실험의 가정
  -> 반복의 원리: 실험을 반복해서 실행해야 함
  -> 랜덤화의 원리: 각 실험의 순서를 무작위로 해야함
  -> 블록화의 원리: 제어해야 할 변수가 있다면 인자에 영향을 받지 않도록 조건을 묶어서 실험해야 함

• 일원 분산분석: 한가지 요인을 기준으로 집단간의 차이를 조사하는 것

• 이원 분산분석: 두 가지 요인을 기준으로 집단 간의 차이를 조사하는 것

• 다원 분산분석: 세 가지 이상의 요인을 기준으로 집단 간의 차이를 조사하는 것

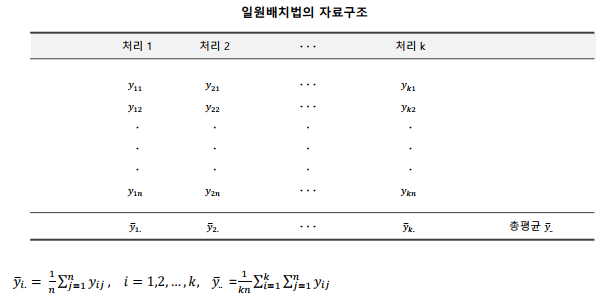
One-way ANOVA

• 한 개의 반응 변수와 한 개의 독립 인자
• 반응 변수: 연속형 변수만 가능
• 독립 인자(변수): 이산형 또는 범주형 변수만 가능
  

• 사후 검정: 평균이 다른건 알지만 어떤 처리 조건이 평균 차이가 있는지?
• Bonferroni., scheffe, Duncan, Dunnett 등의 방법으로 사후 검정이 가능

Two-way ANOVA

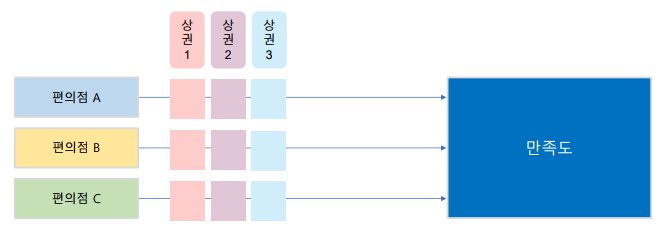
• 한 개의 반응 변수와 두 개의 독립 인자로 분석하는 방법
  -> Ex) 만족도에 영향을 주는 인자가 편의점 브랜드와 상권이라고 할 때, 편의점 브랜드별로 상권을 변경하면서 만족도가 다른지 측정하고 분석하는 방법

• 독립인자는 one-way와 마찬가지로 이산형 또는 범주형 변수만 가능
  

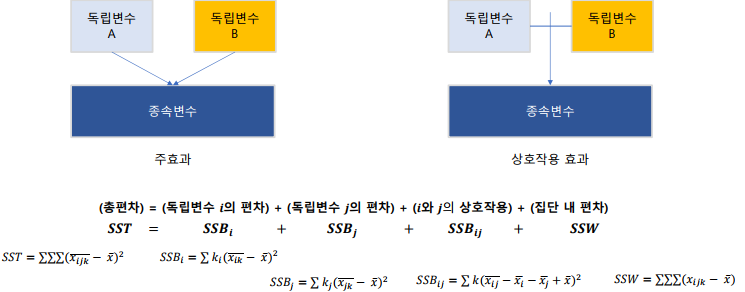
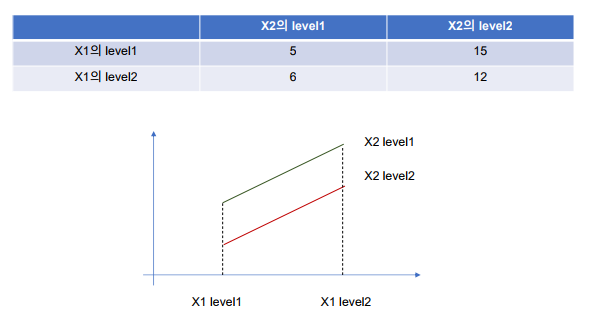
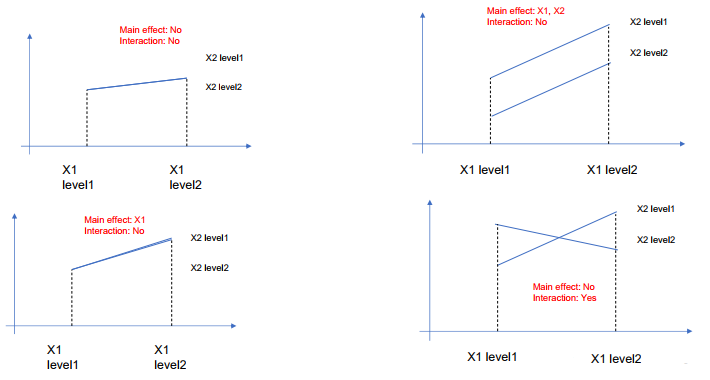
• 상호작용(Interaction effect): 한 독립변수의 main effect가 다른 독립변수의 level에 따라서 원래의 선형관계를 비선형관계로 변하는 경우
  

시계열

• 시계열분석(time series analysis): 시계열(시간의 흐름에 따라 기록된 것) 자료(data)를 분석하고 여러 변수들간의 인과관계를 분석하는 방법

• 시계열데이터
  -> 시계열 데이터는 시간을 기준으로 관측된 데이터로, 보통 일->주->월->분기->년 또는 Hour 등 시간의 경과에 따라서 관측한 데이터
  -> Ex) GDP, 주가, 거래액, 매출액, 승인금액 등을 시간에 흐름에 따라 정의한 데이터
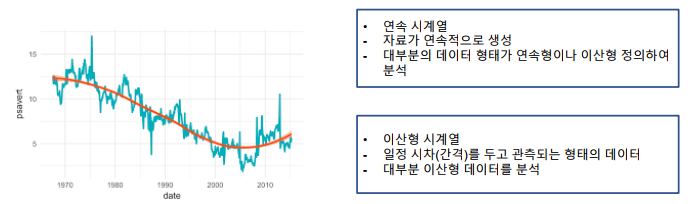
  -> 시계열 데이터는 연속 시계열과 이산 시계열 데이터로 구분할 수 있음
  

• 시계열 분석의 목적
  -> 예측: 금융시장 예측, 수요 예측등 미래의 특정 시점에 대한 관심의 대상(반응변수)을 예측
  -> 시계열 특성 파악: 경향(Trend), 주기, 계절성, 변동성(패턴) 등 관측치의 시계열 특성 파악

전통적인 시계열 분석 방법

• 이동 평균 모형(moving average): 최근 데이터의 평균을 예측치로 사용하는 방법
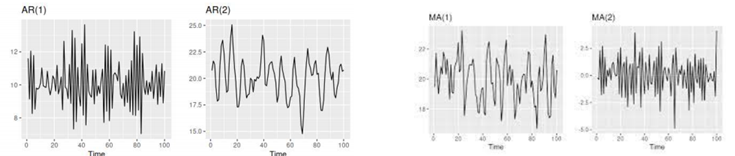
• 자기 상관 모형(Autocorrelation): 변수의 과거 값의 선형 조합을 이용하여 예측하는 방법
• ARIMA(Autoregressive Integrated Moving Average): 관측값과 오차를 사용해서 모형을 만들어서 미래를 예측하는 방법
• 지수평활법: 현재에 가까운 시점에 가장 많은 가중치 주고 멀어질수록 낮은 가중치를 주어서 미래를 예측하는 방법
  

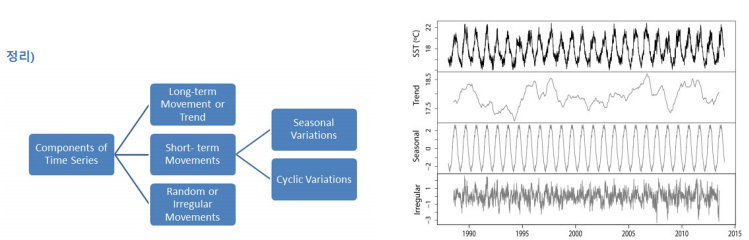
시계열 요소

• 경향/추세(trend): 시계열 데이터가 장기적으로 증가(감소)할 때, 추세가 존재함
• 계절성(seasonality): 특정기간(1년마다) 어떤 특정한 때나 1주일마다 특정 요일에 나타나는 것 같은 계절성 요인이 시계열에 영향을 줄 때 계절성이라 함
• 주기성(cycle): 일정한 주기(진폭)마다 유사한 변동이 반복되는 현상, 보통 경기 순환(business cycle)과 관련이 있으며 지속기간은 2년
• 불규칙요인(Irregular movements): 예측하거나 제어할 수 없는 요소
  

이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다