Outlier Detection for Time Series with Recurrent Autoencoder Ensembles

Outlier Detection for Time Series with Recurrent Autoencoder ensembles

• 2019 International Joint Conference on Artificial Intelligence (IJCAI-19)

Autoencoder ensemble based Time series anomaly detection method

ensemble ➜ overfitting된 일부 autoencoder의 영향을 줄이면서 model의 전반적인 성능을 향상시키는 것이 목표

Introduction

previous autoencoder ensemble methods
➜ time series보다 non-sequential data에 적합했음

time series에 적합한 autoencoder ensemble을 구축하기 위하여, Recurrent Neural Network(RNN)을 사용
➜ sparsely connected RNN을 사용

본 논문에서는 두 가지 방법의 ensemble frameworks를 제안

• Independent Framework(IF)
  여러 autoencoder를 독립적으로 train
  IF trains multiple autoencoders independently
• Shared Framework(SF)
  여러 autoencoder가 함께 train
  SF trains multiple autoencoder jointly through a shared feature space

➜ multiple encoder and decode의 조합을 통한 성능 향상 목적

Contribution

• Sparsely-connected recurrent units을 통해 서로 다른 구조를 가지는 autoencoder 제안

• multiple autoencoder를 활용하는 ensemble frameworks

• autoencoder ensemble method를 time series에 적용

Autoencoder Ensembles For Time Series

본 논문에서는 time series modeling에 효과적이라고 알려진 RNN을 사용하여 autoencoder 구성

Notation

• Time series $T = \left< s_1, s_2, ...\: , s_C \right>$
• Reconstructed time seris $\hat{T}^{(i)} = \left< \hat{s}^{(i)}_{C}, ...\: , \hat{s}^{(i)}_{2}, \hat{s}^{(i)}_{1} \right>$

• $s_i = (s^{(1)}_i, s^{(2)}_i,\: ... \:, s^{(k)}_i)$

  • each vector $s$ represents $k$ features at a time point $t_i$

• num of features $k$

• time series length $C$

$1 \leq i \leq C$
$k = 1$ ➜ univariate
$k > 1$ ➜ multivariate

Autoencoder Ensembles

목표 : autoencoder based anomaly detection method의 성능 향상

서로 다른 autoencoder라고 해도 fully-conneted면 결국 동일한 network이기 때문에 connection이 randomly remove된 sparsely-connected autoencoder를 사용하는 것이 더 좋음

different network structure의 sparsely-connected network를 사용하면 overall reconstruction errors의 variances를 줄일 수 있음

두 프레임워크 모두 시계열의 관측값이 이상치일 가능성을 정량화하는 최종 재구성 오류로 여러 오토인코더의 재구성 오류의 중앙값을 사용합니다

출처 : S-RNNs paper

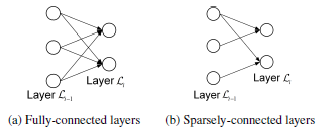
Sparsely-connected RNNs(S-RNNs)

an autoencoder for anomaly detection in time series example

출처 : S-RNNs paper

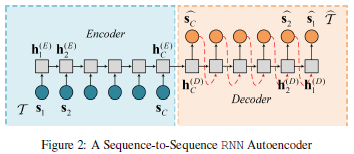
$s$ : time series
$h$ : hidden state

RNN units computation
$h_t = f(s_t, h_{t-1})$
➜ only consider previous hidden state

In previous research proposed
Recurrent Skip Connection Networks(RSCNs)

➜ previous hidden state and additional hidden stated in the past

• Recurrent residual learning for sequence classification (EMNLP, 2016)

hidden state in time step $t$
$h_t = \frac{f(s_t,\:h_{t-1}) \: + \: f'(s_t, \: h_{t-L}) }{2}$

$h_t$는 이전 hidden state인 $h_{t-1}$ 뿐만 아니라 $L$ 시점 이전의 hidden state $h_{t-L}$도 함께 고려 (같은 비중으로)

In this paper, proposed
Sparsely-connected RNNS(S-RNNs)

RSCNs + randomly remove some connections bewteen hidden states
➜ sparseness weight를 사용해서 random connection 생성

sparseness weight vector $w_t = (w^{(f)}_{t}, w^{(f')}_{t})$
$w^{(f)}_{t} \in \left\{0, 1 \right\}$
$w^{(f')}_{t} \in \left\{0, 1 \right\}$

weight vector는 0 or 1의 값을 가짐
0 ➡ disconnected
1 ➡ connected

$h_t = \frac{f(s_{t}, \: h_{t-1}) \cdot w^{(f)}_{t} \: + \: f'(s_t, \: h_{t-L}) \cdot w^{(f')}_{t}}{\left\|w_{t} \right\|_{0}}$

$\left\|w_{t} \right\|_{0}$ : the number of non-zero elements in vector $w_t$

RCSN and S-RNN example

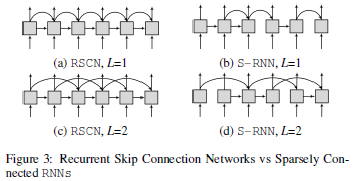
RSCN은 모든 hidden state가 $L$ 시점 이전의 hidden state를 매번 고려하지만, S-RNN은 이전 hidden state를 고려하는 state가 randomly select

본 논문에서 언급하는 RNNs with dropout과 S-RNNs의 다른 점

• S-RNN : fixed throughout the training phase
• RNN with dropout : randomly remove connections at every training epoch

S-RNN Autoencoder Ensembles

In this paper, proposed two different frameworks

Independent Framework(IF)

총 $N$개의 S-RNN autoencoder를 사용
각 autoencoder는 독립적으로 학습되며, 각각의 sparseness weight vector가 존재

Loss function
$J_i = \sum^{C}_{t=1}{\left\|s_{t} - \hat{s}_{t}^{(D_i)} \right\|}_{2}^{2}$

$\hat{s}_{t}^{(D_i)}$ : reconstructed vector at time step $t$ from decoder $D_i$

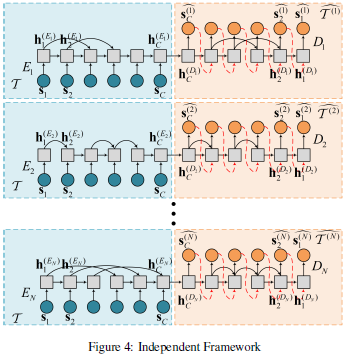
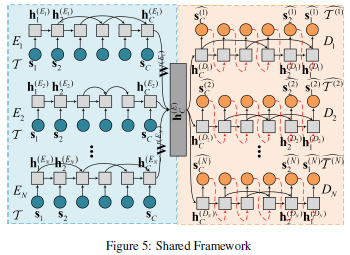
Shared Framework(SF)

IF의 경우 training phase동안 autoencoder 간의 interation이 존재하지 않음
but 모든 autoencoder는 결국 original input을 reconstruction하는 것이 목표이기 때문에 autoencoder 간의 상호 작용이 의미가 있음
➜ multi-task learning 적용

original input data를 reconstruction 하는 $N$개의 task(encoder)가 주어지면 각 encoder output이 shared layer를 통해 공유

$h^{(E)}_{C}$ : shared layer
➜ 모든 encoder의 last hidden states
를 linear combination을 통해 concat

$W^{E_i}$ : linear weight matrices

$h^{(E)}_{C} = concatenate(h_{C}^{(E_1)} \: \cdot \: W^{(E_1)}, \:...\: , h_{N}^{(E_N)})$

각 decoder는 concatenated hidden states 를 initial hidden state로 사용해서 input으로 사용된 time series를 reconstruction

모든 autoencoder는 하나의 loss function 함께 train

Loss Function

$J = \sum^{N}_{i=1}J_i + \lambda{\left\| h_{C}^{(E)} \right\|}_1$

$\:\:\:\:\:= \sum^{N}_{i=1}\sum^{C}_{t=1}{\left\|s_t - \hat{s}^{(D_i)} \right\|_{2}^{2}} + \lambda{\left\| h_{C}^{(E)} \right\|}_1$

$\lambda$ : L1 regularization의 weight control parameter

loss function은 모든 autoencoder의 reconstruction error의 합산과 L1 regularization term으로 구성

• L1 regularization
  • 핵심 feature들만 남기기 위해서 사용
    → 너무 작은 weight들은 0이 되어 중요한 weight들만 남게 됨
    
  • shared hidden state를 sparse하게 만드는 효과
  • 일부 encoder가 overfitting되는 경우 방지 & decoder를 robust하게

➜ autoencoder가 anomalous value를 만나면 residual의 차이가 더욱 커짐

Anomaly score

original time series $T$에 대한 autoencoder 개수 $N$개 만큼의 reconstructed time series가 도출되며 이에 따라 $N$개의 reconstructed error 생성
reconstructed error $\left\{\left\| s_k - \hat{s}_{k}^{(1)} \right\|_{2}^{2}, \left\|s_k - \hat{s}_{k}^{2} \right\|_{2}^{2} , ...\:, \left\|s_k - \hat{s}_{k}^{N} \right\| \right\}$

final anomaly score
$anomaly \: score(s_k) = median(\left\{\left\| s_k - \hat{s}_{k}^{(1)} \right\|_{2}^{2}, \left\|s_k - \hat{s}_{k}^{2} \right\|_{2}^{2} , ...\:, \left\|s_k - \hat{s}_{k}^{N} \right\| \right\})$

overfitting된 reconstruction errors의 영향을 감소시키기 위해 mean대신 median을 사용

Experiments

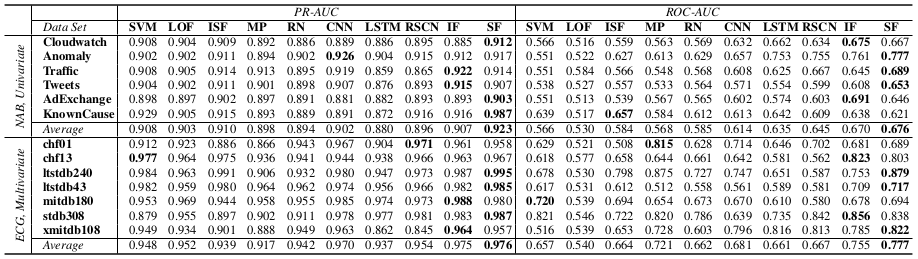
evaluation metirc : RP-AUC, ROC-AUC

대부분의 dataset에서 SF가 IF보다 좀 더 높은 성능을 보임을 확인할 수 있음

Concolusion

• Sparsely-connected RNN 사용

• 두 가지 방법의 RNN based autoencoder ensemble frameworks

  • 각 autoencoder를 독립적으로 학습
  • autoencoders를 동시에 학습