Outlier Detection with Autoencoder Ensembles

Outlier Detection with Autoencoder Ensembles

• 2017 SIAM International Conference on Data Mining (SDM)

Introduction

In this paper, authors proposed autoencoder ensemble method
: Randomized Neural Network for Outlier Detection(RandNet)

fully connected autoencoder 대신 randomly connected autoencoder를 사용
각 autoencoder는 structures와 connection densities가 서로 다름
➜ computational complexity ↓

Deep Neural Network의 overfitting 위험성이 존재하며 종종 local optima로 수렴
➜ 일부 structure가 overfit 되더라도 emsemble의 특성인 다양성으로 인하여 전반적으로 효율성이 향상될 수 있음

RandNet

Autoencoder based model
➜ input과 output이 최대한 비슷하게 reconstruction하도록 model training
➜ latent vector는 input의 주요한 특성을 포함하고 있을 것
➜ anomaly는 잘 reconstruction x

fully connected auto-encoder example

출처 : RandNet paper

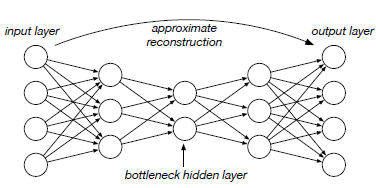
train data에 anomaly가 포함되어 있는 경우가 많아 neural networks based methods 학습 시에 overfitting의 가능성이 높아짐

➜ overfitting의 문제 해결하기 위해 ensemble method 적용

but multiple methods의 조합이 항상 best performance를 보이는 individual model보다 더 나은 결과를 보인다고 보장할 수는 없음
따라서, ensemble method가 잘 작동하기 위해서는 각 구성 요소가 충분히 다양해야 함
다양한 구조가 조합되면 서로 다른 패턴을 포착하기 용이할 것

본 논문에서는 fully connected autoencoder를 사용하면 각 model의 output이 비슷할 것이기 때문에 randomly connected autoencoder를 사용

randomly connected auto-encoder example

출처 : RandNet paper

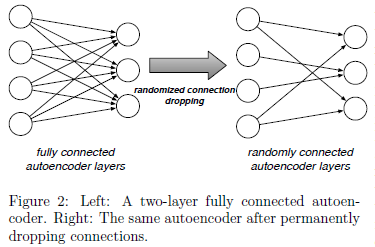
RandNet과 dropout의 차이점

• RandNet : 서로 다른 구조의 NN model의 결과가 합쳐짐 ➜ 단일 구조의 overfitting의 큰 문제 없음
• Dropout : 단일 모델 내의 random connection ➜ overfitting 방지 목적

Neural Network Structure

autoencoder structure
각 layer에서 사용되는 node 수는 이전 layer의 node의 $\alpha$ 비율로 설정되며 최소 node 수는 3
➜ botteleck hidden layer에서 과도한 압축으로 인하여 발생하는 정보 손실을 막기 위해

Activation Function

첫 번째 hidden layer와 output layer : Sigmoid function
나머지 layer : ReLU

두 activation function의 장/단점의 균형을 맞추는 것을 목표로 하며,
해당 activation function 조합을 사용하였을 때 가장 좋은 성능을 보임

Anomaly score

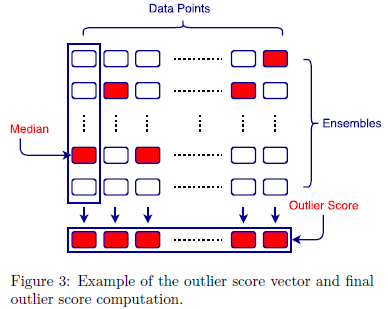
notation

• $n$ : the number of data points
• $d$ : data dimension
• $m$ : ensemble components

$x_{ij} \in \mathbb{R}^{d}$ : $i$-th ensemble component's $j$-th input data point
$o_{ij} \in \mathbb{R}^{d}$ : autoencoder's reconstructed output

$[OS_i]_j = \sum_{k=1}^{d}([x_{ij}]_k - [o_{ij}]_k)^2$

$i \in 1 ... m, \: j \in 1 ... n$

data point의 final anomaly score는 ensemble의 median score로 계산

Conclusions

In this paper ...

• autoencoder ensemble
• adaptive data sampling
  : training iteration에 따라 sampling size를 증가시키며 학습