A Deep Neural Network for Unsupervised Anomaly Detection and Diagnosis in Multivariate Time Series Data
A Deep Neural Network for Unsupervised Anomaly Detection and Diagnosis in Multivariate Time Series Data
- 2019 AAAI Conference on Artificial Intelligence
- mutlivariate time series anomaly detection method
- signature matrix
multivariate time series의 각 time series 사이의 inter-correlation을 사용한 signature matrix를 input으로 사용
Introduction
multivariate time series anomaly detection
previous anomaly detection methods
ex) distance/clustering method(kNN), classification methods(OC-SVM), density estimation methods(Deep Autoencoding Gaussian Mixture Model; DAGMM)
➜ they cannot capture temporal dependencies across different time steps
위의 한계점을 보완하기 위하여 signature matrix를 제안
서로 다른 time step 사이의 정보를 multiple level로 표현하는 multi-scale(resolution) signature matrices 생성하여 temporal information을 활용
Contributions
- Convolutional encoder : encode the inter-sensor correlations
- Attention based ConvLSTM : incorporate temporal patterns
- considers correlations among multivariate time series
MSCRED Framework
Multi-Scale Convolutional Recurrent Encoder-Decoder (MSCRED)
- encode the spatial information in signature matrices via a convolutional encoder
- model the tmeporal information via an attention based ConvLSTM
- reconstruct signature matrices based upon a convolutional decoder
Notation
: multivariate time series
: time series with length
: window size
Signature Matrix
- Time series 사이의 correlation을 확인하는 것은 system status를 파악하는데 중요
- Multivariate time series의 각 time series 간의 inter-correlation을 나타내기 위하여 Signature Matrix를 제안
- window 내에서의 correlation에 초점을 맞춤
- two time series의 inner-product를 사용해서 correlation 계산
➜ capture the shape similarities and value scale correlations between two time series
➜ robust to input noise
: 특정 구간에 anomaly가 존재하더라도 해당 data가 signature matrix의 생성 과정에서 미치는 영향이 작음
-dim의 multivariate time series의 시점까지의 signature matrix
의 sub-time series and
두 time series의 correlation
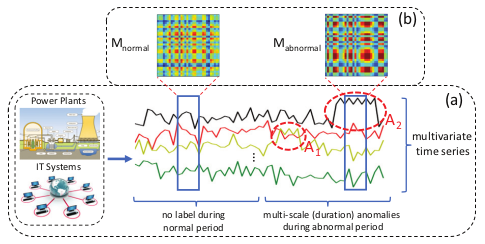
(a) Multivariate time series example
(b) Signature matrix example
본 논문에서 사용한 segment 관련 size
- hop size : 10
- window size : 10, 30, 60
다양한 size를 사용하여 signature matrices 형성 후 concat해서 사용
window size가 anomaly 판단에 영향을 줄 것
총 5쌍의 signatur matrices를 사용함
Signature Matrix example
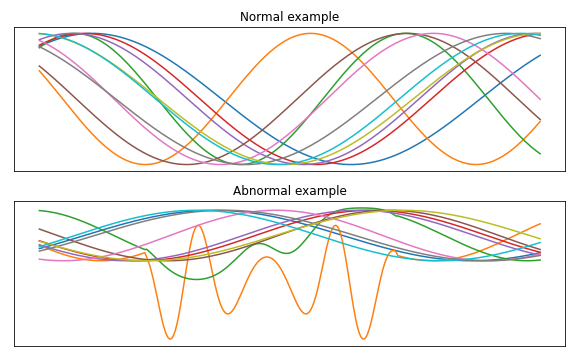
synthetic data의 일부를 example로 사용
정현파로 구성된 normal data와 이상치가 주입된 일부 구간의 anomaly data
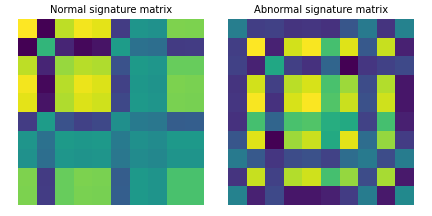
위 구간의 data를 signatur matrix로 표현한 모습
➜ normal 구간의 signature matrix와 abnormal 구간의 signature matrix의 형태가 다른 것을 확인할 수 있음
Framework
MSCRED의 구조는 아래와 같음
전체적으로 autoencoder의 구조를 사용하고 있음
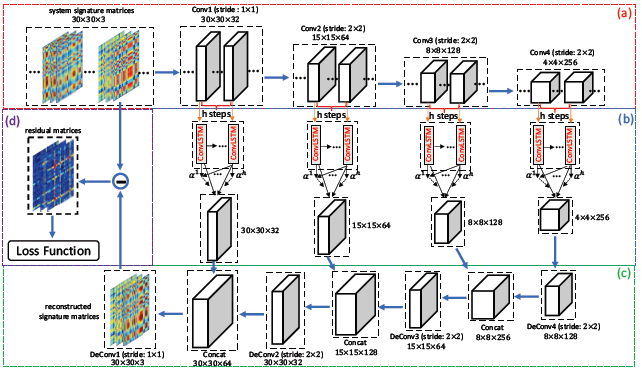
(a) Convolutional Encoder
signature matrice의 spatial pattern을 포착하는 것이 목표
(inter-time series correlation patterns)
CNN으로 구성된 총 4개의 fully convolutional encoder를 사용
(b) Attention based ConvLSTM
- Convolutional lstm network: A machine learning approach for precipitation nowcasting (Shi et al. 2015, NIPS)
- 기존 LSTM의 spatio 특성을 잘 반영하지 못하는 약점을 보완하기 위해 제안
- LSTM 내부 연산이 convolutiond으로 이루어져 spatio-temporal information을 동시에 학습할 수 있음
ConvLSTM을 사용하여 spatio-temporal information을 동시에 학습할 수 있지만, 여전히 sequence length가 길어질수록 성능 저하가 발생
➜ 이전 time step의 signature matrices와의 attention을 사용하여 보완하고자 함
본 논문에서는 step length를 5로 설정하여 이전의 feature maps와의 attention을 확인
각 encoder layer를 통과한 feature maps를 ConvLSTM layer를 통해 temporal information을 추출한 hidden state를 생성
➜ 각 시점의 hidden state 간의 attention을 수행(stnd : last feature map)
➜ feature maps 생성
(b)의 최종 feature map은 spatio-temporal informateion을 모두 포함하고 있을 것
(c) Convolutional Decoder
input으로 사용된 signature matrices를 reconstruction하기 위해 총 4개의 deconvolutional layer를 사용
각 위치의 ConvLSTM layer의 output과 이전 decoder의 output을 concat
➜ 다음 decoder의 input으로 사용
ConvLSTM layer의 output과 DeConv layer의 output을 결합함으로써 더 나은 anomaly detection performance를 기대할 수 있다고 함
모든 decoder를 거친 후엔 input으로 사용된 signature matrices 중에서 가장 마지막 시점의 signature matrices가 reconstruction 됨
(d) Calculate Residual Matrices
본 논문에서는 총 5 time step을 input으로 사용
복원 시에는 last time step의 signature matrices를 복원
시점의 signature matrices와 reconstructed signature matrices 간의 차이로 residual signature matrices를 구함
➜ MSE loss를 사용하여 model training
Conclusion
- original time series대신 signature matrices라는 새로운 input 형태를 도입
- signature matrix는 각 univariate time series 간의 inter-correlation을 기반으로 형성
- training process 동안 inter-correlation과 temporal dependencies를 train
- poorly reconstructed row/column ➜ anomaly root cause 판단