[머신러닝 1강] Feature Extraction

1. 특징 추출(Feature Extraction)

Data

• A set of samples
  • $(D = \{x_i\}_{i=1...N}, D=\{(x_i, y_i)_{i=1...N}\})$

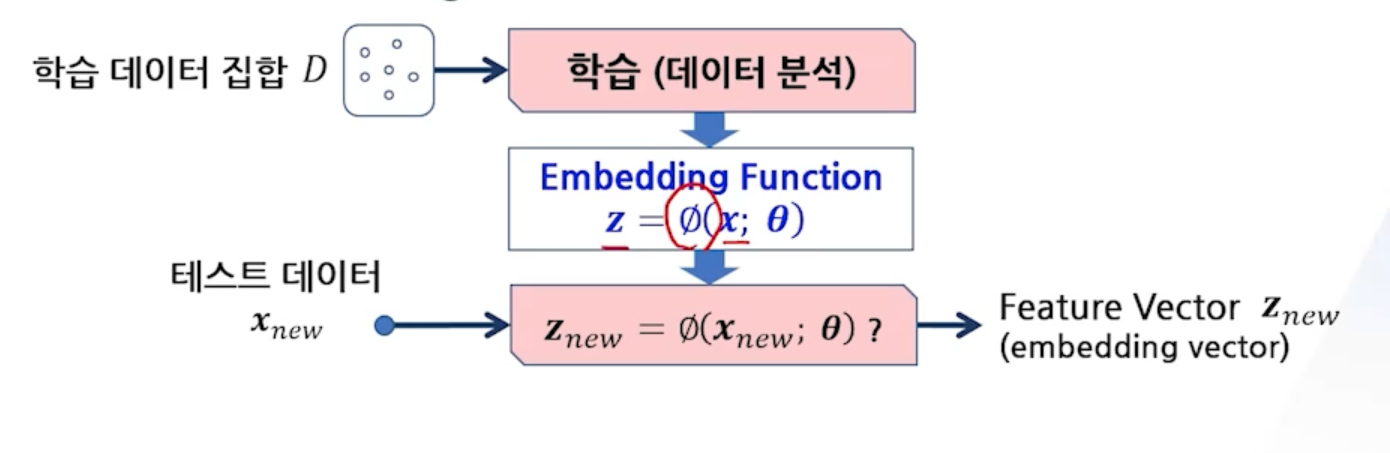
• Goal of Learning
  • 분석에 필요한 정보만 추출 (구체적 분석 목적에 따라 달라짐)

A) 변환 함수의 종류

선형 변환 (Linear Transformation)

• $y = \phi(x) = W^Tx$
• m차원 열벡터 $x$에 변환행렬 $W(m \times d)$를 곱하여 $d$차원 특징을 획득
• 통계적 방법
  • 특징벡터 y가 원하는 분포가 되도록 하는 W를 찾음

비선형 변환 (Non-Linear Transformation)

• 복잡한 비선형 함수 $\phi(x)$를 이용하여 $m$차원 벡터를 $d$차원 벡터로 매핑

2. 선형변환에서의 특징 추출

A) 차원 축소 관점에서의 특징 추출

• $m$차원 데이터 $x$를 행렬 $W(m \times d)$에 의해 $d$차원 특징 $y$로 매핑 $(m > d)$
  • $y = W^Tx$

$\begin{bmatrix}y_1\\y_2\\y_3\\...\\...\\y_d\end{bmatrix}$ = $\begin{bmatrix}w^T_1x\\w^T_2x\\w^T_3x\\...\\...\\w^T_dx\end{bmatrix}$ = $\begin{bmatrix}w^T_1\\w^T_2\\w^T_3\\...\\...\\w^T_d\end{bmatrix}x$ =

$\begin{bmatrix}w_1,&w_2,&w_3,&...&...&w_d\end{bmatrix}$ = $W^T_x$

• 특징값 y_i
  • x를 W의 열벡터 W_i위로 사영한 값

B) 전체 데이터 집합 $X$에 대한 특징 추출

• $X = [x_1, x_2..... x_N]$ $(m \times N)$행렬
• $Y = [y_1, y_2..... y_N]$ $(d \times N)$행렬

$Y = W^TX = [W^T_{x_1}, W^T_{x_2}, W^T_{x_N}]$

즉, 선형변환 특징추출이란

주어진 데이터를 변환행렬 W에 의해 정해지는 방향으로 사영함으로 저차원의 특징값을 얻는 것

C) 선형 변환 방법

PCA (주성분 분석)

• 클래스 정보 미사용
• 차원을 축소할 때 손실되는 데이터를 최소화하는 것이 목표

LDA (선형판별분석)

• 클래스 정보 사용
• 분류가 잘 될 수 있도록 변환행렬을 만드는 것이 목표

3. PCA

목적

• 변환 전의 데이터 $x$가 가지고 있는 정보를
  차원 축소 후에도 최대한 유지

  • 데이터 집합이 가능한 넓게 퍼질 수 있는 방향으로
    사영을 수행 해야한다.

    • 즉, 데이터의 분산이 가장 큰 방향으로의 선형 변환 수행
    • 가장 큰 분산과 그 방향 =
      공분산 행렬의 최대 고유치와 고유벡터

데이터의 공분산 행렬의 고유치와 고유벡터를 찾아,
고유치가 가장 큰 값부터 순서대로 이에 대응하는
$d$개의 고유벡터를 찾아서 행렬 $W$를 구성

수행 단계

1. 입력 데이터 집합 $X$의 평균과 공분산 계산

2. 고유치 분석을 통해 공분산의 고유치 행렬과 고유벡터 행렬을 계산

3. 고유치가 큰 것부터 순서대로 $d$개의 고유치를 선택

4. 선택한 고유치에 대응되는 고유벡터를 열벡터로 가지는 변환행렬 $W$를 생성

5. $W$ 에 의한 선형변환으로 특징 데이터 $Y$를 얻음