1. 압축 알고리즘
주어진 데이터의 의미를 바꾸지 않으면서,
더 적은 저장 공간에 효율적으로 기록하기 위함.
압축률
- 인코딩 전의 데이터 크기와 인코딩 이후 데이터 크기의 비율
- 인코딩 전의 데이터 크기에 비해 인코딩을 통해 줄어든 데이터 크기의 백분율
알고리즘 분류
무손실 vs 손실
- 디코딩을 통해 원래 데이터의 완전한 복원 여부에 따른 분류
- 무손실
- 파일 압축 -> zip
- 손실
- 멀티미디어 데이터 -> mp3, jpeg, mpeg 등
무손실 압축 알고리즘
| 저장방법 / 압축단위 | Block-to-Variable | Variable-to-Variable |
|---|---|---|
| 사전이 없는 방법 | differential 인코딩 | RLE |
| 사전이 고정된 방법 | 통계적인 인코딩(허프만 코딩) | factor 인코딩 |
| 동적으로 사전을 생성 | 순차적인 통계 인코딩(Faller and Gallager) | Ziv-Lempel 알고리즘 |
2. 사전이 없는 압축
RLE
Run Length Encoding
- 동일 문자가 연속적으로 나타나는 경우,
이를 반복 개수로 줄여서 표현- 반복 개수가 3개 이상이어야 효과적
- 일반 문서에서는 비효율적
- 0/1이 계속적으로 나타나는 영상 데이터 압축에 효과적
ex)
aaabbbbbaaccccbaaaaaa
- &3a &5b &2a &4c b &7a
Differential 인코딩
비슷한 값이 연속적으로 나타날 때, 앞의 값과의 차이만을 기록하여
출력 비트수를 줄이는 방법
- 상대적인 인코딩
- 어떤 값의 연속된 버전을 저장하는 데 주로 사용
- ->
ex)
2016, 2017, 2015, 2017, 2018, 2015, 2015, 2013,....
- 2016, 1, -2, 2, 1, -3, 0, -2, ....
3. 허프만 코딩
문자가 텍스트에서 출현하는 빈도에 따라 다른 길이의 부호를 생성
- 많이 나타나는 문자
- 짧은 부호
- 드물게 나타나는 문자
- 긴 부호
- 허프만 코딩은 문자의 빈도 또는 확률 정보를 이용한 압축 방법이기 때문에,
통계적 압축법이라고 부르기도 한다.
코드워드 codeword,
- 알파벳 의 각 문자에 대응하는 부호
- 코드워드의 집합 -> 코드
- , -> 의 빈도, 확률
ex) abracadabra 인코딩
8비트 아스키로 표현하는 경우
- 11문자 x 8비트 = 88비트
고정길이 코드로 표현하는 경우
- 영문자 26자 -> 각 문자당 5비트 필요
- 11문자 x 5비트 = 55비트
빈도 수에 따른 가변길이 코드로 표현하는 경우
-
빈도수
- a >> 5
- b >> 2
- c >> 1
- d >> 1
- r >> 2
-
가변길이 코드 ( 많이 나타나는 문자는 짧은 코드 부호 )
- a >> 0
- b >> 1
- r >> 00
- c >> 01
- d >> 10
-
인코딩 후 모습
- 010000101001000 (15 비트)
하지만 위 15비트는 문제가 있다.
언제 문제가 생기냐면, 바로
디코딩할 때 문제가 생긴다.
위 010000101001000의 15비트를 디코딩해보겠다.
- 디코딩
- abra.... (제대로 디코딩 한 경우)
- adar.... (2, 3번째 비트를 d로 해석한 경우)
- crad.... (2, 3번째 비트를 c로 해석한 경우)
즉, 디코딩을 할 수 없어진다. 그래서 아래의 코드가 등장하게 된다.
접두사 코드, 최적 코드
접두사 코드
어떠한 코드워드도 다르 코드워드의 접두사와 일치하는 경우가 없는 코드
- 모호함 없이 디코딩이 가능하다.
- 예를 들어 어떤 문자 X의 코드워드가 011이라고 가정하자.
- X의 코드워드인 011의 접두사는 아래와 같다.
0
01
011- 다른 문자의 코드워드는 011의 접두사는 사용할 수 없다는 것이
접두사 코드라고 한다.
최적 코드
인코딩된 메세지의 길이가 가장 짧은 코드
또는 의 값을 최소로 하는 코드
기본 정보 이론 by Shannon
의 엔트로피
의 엔트로피
코드의 평균 길이
기본 정보이론에 따르면 최적 코드는
코드의 평균길이가 C의 엔트로피와 같아지는 지점을 말한다.
즉, 비트인 코드를 말한다.
이 때 는 각 코드워드의 길이를 뜻한다.
[정리]
어떤 정해진 길이의 모호함이 없는 코드가
존재할 필요충분조건은 동일 길이의 접두사 코드가 존재하는 것이다.
by Kraft 부등식 & McMillan 부등식
따라서 허프만 코딩은 아래의 과정을 거친다.
-
최적 접두사 코드 생성
-
인코딩
-
소스 텍스트에서 각 글자의 빈도수 계산
-
각 글자들의 빈도를 이용하여 상향식(Bottom-Up)으로
이진 나무( 허프만 나무 ) 를 만들고 코드워드 할당 -
소스 텍스트의 각 글자를 코드워드로 변환하여 압축된 텍스트 생성
-
허프만 나무
각 글자에 이진 코드를 부여하기 위해서
상향식으로 만드는 이진 나무
- Leaf Node는 각 문자를 나타내는 Full 이진 트리
- 각 Node는 빈도수로 레이블 됨
- 좌우의 두 간선은 각각 0와 1로 레이블 됨
허프만 나무 생성 과정
-
각 문자가 노드 하나로 구성된 나무인 상태로 시작
-
빈도수가 작은 두 나무를 합쳐, 큰 나무를 생성하는 과정을 반복
- 부모 노드의 빈도수는 두 자식 나무의 빈도수의 합과 같다.
HuffmanTree(C[], F[], n) {
# 입력:
C[1...m] -> 알파벳
F[1...m] -> 문자 c_i의 빈도수
n -> 길이
# 출력:
Q: 허프만 나무
# 성능:
O(nlogn)
#################################
빈도수 F[]에 따라 최소 힙 Q 생성; # O(n)
for (i=1; i<n; i++) { # O(n)
u <- 힙 Q에서 최솟값 삭제;
v <- 힙 Q에서 최솟값 삭제;
# 위 두 과정 합쳐서 O(logn)
새 노드 x를 생성하여 u와 v를 x의 두 자식 노드로 지정;
노드 x의 빈도수 <- u의 빈도수 + v의 빈도수;
노드 x를 힙 Q에 삽입;
}
return Q;
}Ex) abracadabra를 다시 인코딩 해보자
빈도수 계산
- a 5번
- b 2번
- r 2번
- c 1번
- d 1번
빈도수가 가장 작은 두 노드를 선택해서 합침
- 허프만 트리 생성
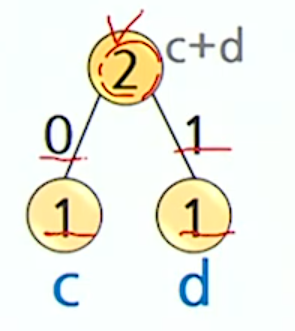
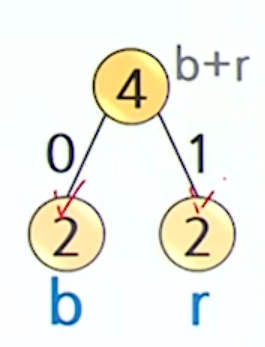
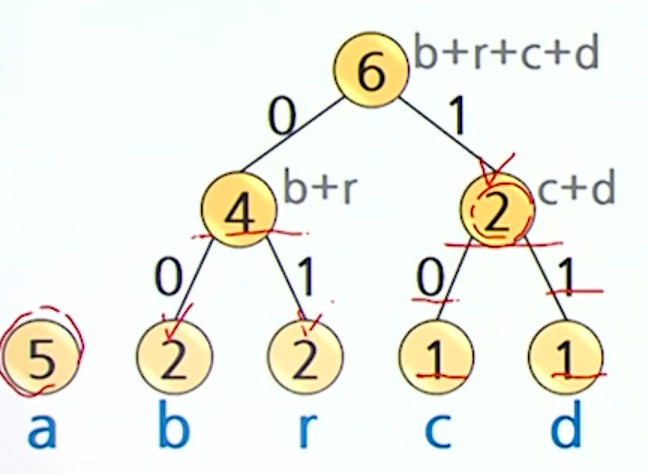
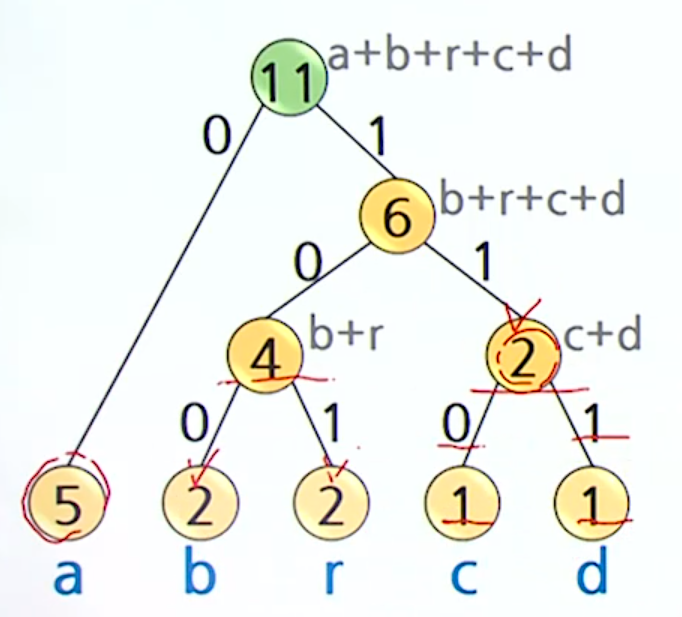
코드워드 할당
- 간선의 레이블을 합침
| 문자 | 코드 |
|---|---|
| a | 0 |
| b | 100 |
| c | 110 |
| d | 111 |
| r | 101 |
인코딩 결과
01001010110011101001010 ( 23비트 )
디코딩
압축된 데이터를 1비트씩 읽으면서, 허프만 나무를 따라 내려오다가
Leaf Node에 도착할 때마다 Leaf Node에 해당하는 문자를 출력하고
다시 Root Node로부터 반복
허프만 코딩의 문제점!!!!!!!!!!
각 문자의 빈도수를 모르는 경우에는 소스 텍스트를 두 번 읽어야 한다.
- 각 문자의 빈도수 계산
- 실제 인코딩 과정
-> 실용성이 없다. ( 동적 허프만 코딩으로 해결 가능 )
압축된 데이터를 디코딩 하기 위해 빈도수, 허프만 나무, 알파벳에 대한 정보가 필요하다.
- 허프만 나무는 최대 개의 Node를 가지므로
각 문자의 길이가 k비트라면 약 비트의 정보가
헤더로 제공된다.- 실제 압축률 저하 초래
4. 동적 허프만 코딩
문자의 빈도수를 만들어 나가면서 코딩
- 텍스트를 한 번만 읽으면 됨.
- 적응적 (adaptive) 허프만 코딩이라고 부른다.
- 빈 나무에서 시작해서 텍스트의 문자를 하나씩 읽어 들이면서
허프만 나무를 만듦과 동시에 인코딩/디코딩 수행
실제로 UNIX의 compact 명령어가
동적 허프만 코딩을 사용하고 있다.
인코딩 과정
-
이라고 가정 -> 빈도수 0
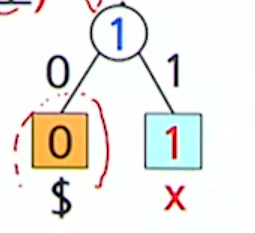
- 임의의 문자를 지정 (위에서는 $표시를 지정한 것임)
-
$ 하나로 이루어진 나무에서부터 시작
-
읽어들인 문자가 새 문자? 앞서 나왔던 문자?
-
앞서 나온 문자
- 출력(허프만 나무에서 부여된 코드워드), 빈도수++
-
입력에서 처음 등장한 문자
- 출력 ($의 코드워드 + 원래의 기호 그대로)
- x 노드 삽입
-
DynamicHuffman(Text) {
빈도는 0이고 이름은 $인 한 노드로 구성된 초기 나무 T를 생성;
while(Text의 끝이 아님) {
x = Text의 다음 문자;
if (x가 T에 이미 있으면) {
T에서 x에 부여된 코드워드 출력;
x의 빈도를 하나 증가;
}else {
$의 현재 코드워드와 x의 기호 출력;
v = 현재의 $ 노드;
v의 왼쪽에 $ 노드, 오른쪽에 입력 문자 x의 노드 생성;
v, v의 왼쪽, v의 오른쪽의 빈도를 각각 1,0,1로 설정;
}
}
# 형제 성질이 유지되도록 나무를 조정 O(n)
# 핵심 함수
ADJUST(T);
}[정리] 형제 성질
T를 가중치가 부여된 Full 이진 트리라고 하자.
-
T의 내부 노드는 두 자식 노드의 합이 가중치이다.
-
T가 허프만 나무일 필요충분조건은
아래의 두 조건을 만족하도록 하는 노드들의순열 이 존재하는 것이다.-
를 노드 v의 가중치라 할 때, 이 오름차순이다.
-
인 모든 i에 대하여, 과 는 형제이다.
즉, 그 둘은 같은 부모의 자식이다.
-
ADJUST(Text){
as
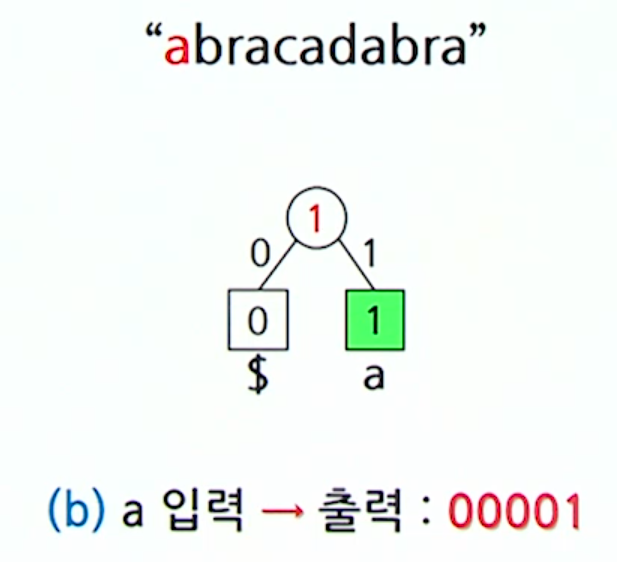
}Ex) abracadabra 동적 허프만 코딩
- a: 00001
- b: 00010
- c: 00011
- d: 00100
- r: 10010

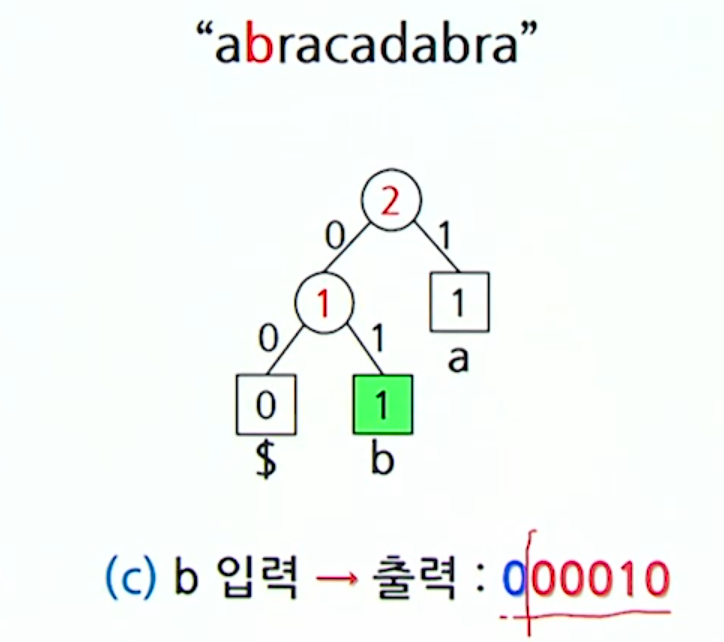

r를 삽입하고 나니, 형제 성질을 만족하지 않기 때문에 조정과정을거친다.

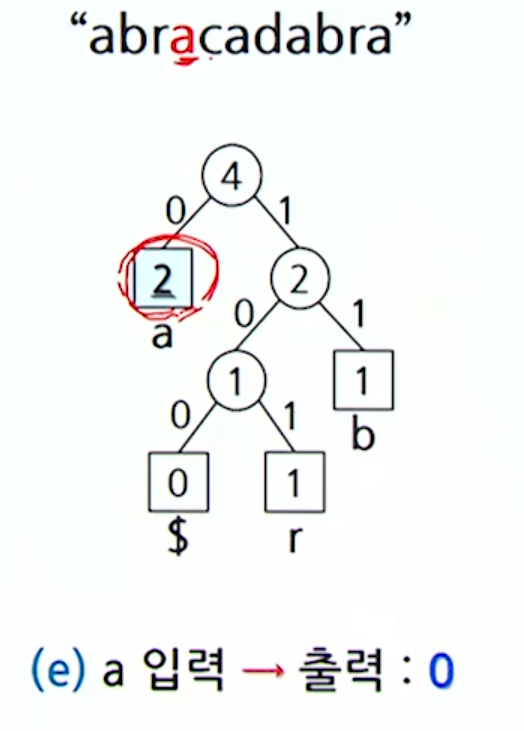
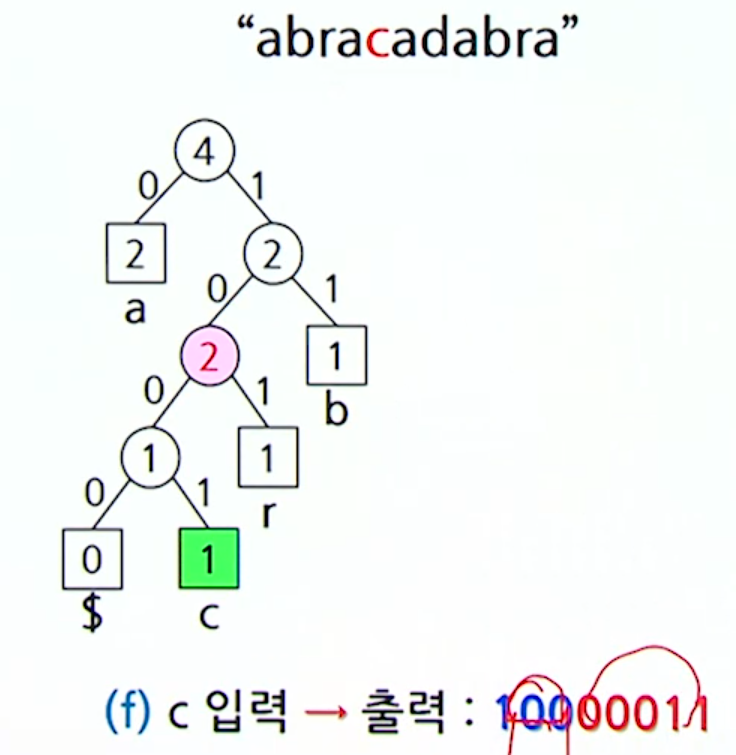
c를 삽입하고 나니, 형제 성질을 만족하지 않기 때문에 조정과정을거친다.
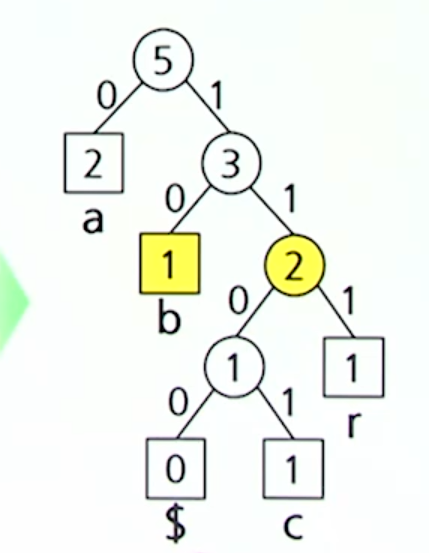
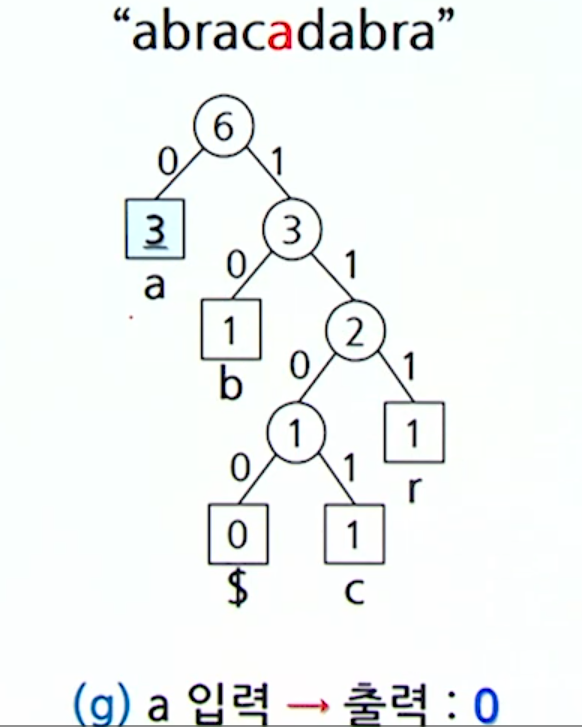
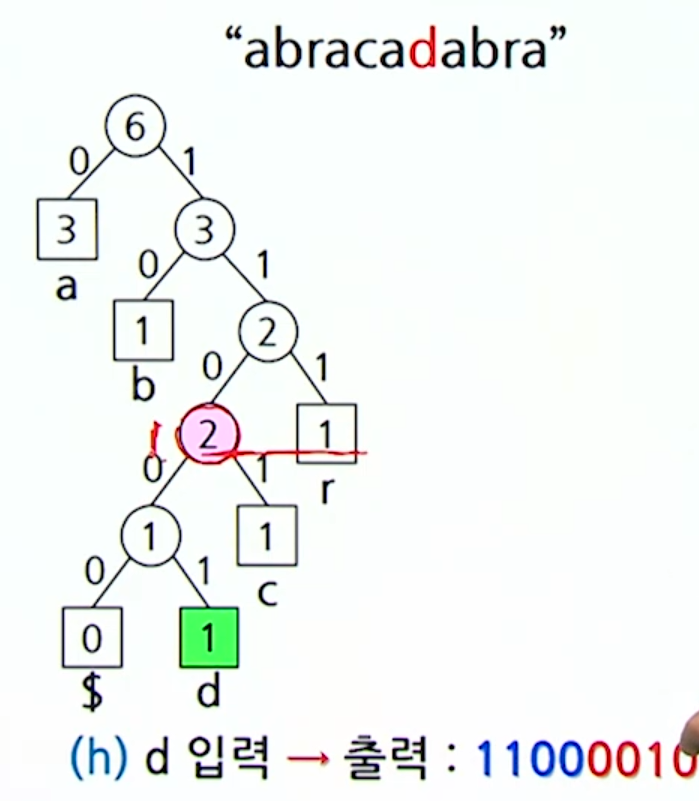
d를 삽입하고 나니, 형제 성질을 만족하지 않기 때문에 조정과정을거친다.
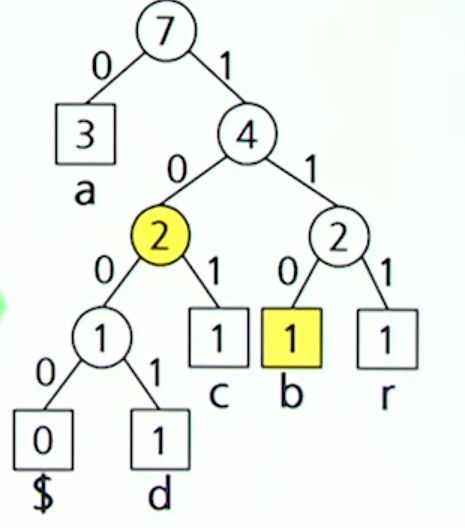
위 방법을 계속 반복한다.
인코딩 된 값
000010000100010010010000011011000010001101100
디코딩
인코딩 과정과 대칭적으로 수행
-
압축되지 않은 코드
- 그대로 출력하고 나무에 삽입하여 코드를 부여
-
압축된 코드
- 현재 나무로부터 그것이 어떠한 기호인지를 알아내고
빈도수를 하나 증가
- 현재 나무로부터 그것이 어떠한 기호인지를 알아내고
