[알고리즘 10강] 스트링 매칭2

1. 아호-코라식 알고리즘

다중 키워드 매칭 알고리즘으로,
주어진 패턴들을 이용하여 단어 나무를 생성하고
텍스트를 왼쪽에서 오른쪽으로 스캔하면서 단어 난무에서 패턴을 매치 시킴

• $O(m_s + n)$

다중 키워드 매칭 알고리즘

• 패턴의 집합 $P=\{P_1, P_2, ..., P_q\}$
• $m_s = \vert P_1 \vert + \vert P_2 \vert + \vert P_3 \vert + ... + \vert P_q \vert$

단어 나무

패턴의 집합 $P=\{P_1, P_2,...,P_q\}$에 대한 단어 나무 W는
뿌리 나무로서 다음의 네가지 조건을 만족한다.

• 모든 edge(간선)은 하나의 문자로 레이블 된다.

• 동일 node에서 나가는 둘 이상의 간선은 서로 다른 문자로 레이블된다.

• W의 Root Node r로부터 어떤 node x까지에 이르는
  경로상의 문자들을 차례대로 접속한 것을 word(x)라 하면,
  word(x)는 어떤 패턴 $P_i$의 접두부가 된다.

• 또 $P_i \in P$에 대하여, $P_i = word(v)$인 node v가 W에 존재한다.
  leaf Node x의 word(x)는 반드시 어떤 $P_i$와 같아야한다.

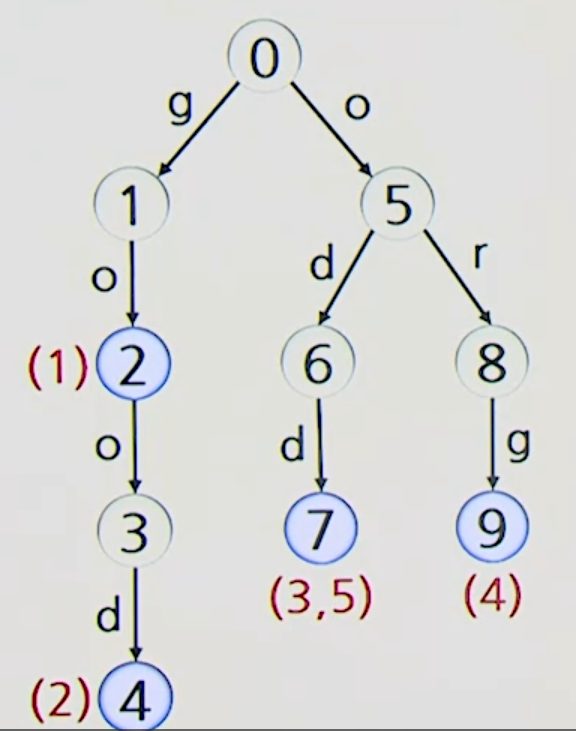
예제 $P = \{go, good, odd, org, dd\}$

매칭 과정 (Naive vs 아호 코라식)

Naive 다중 키워드 매칭

텍스트의 각 위치에서 단어 나무의 Root Node로부터 따라 내려가면서 매칭 수행

• 도중에 불일치가 발생하면, 텍스트의 다음 위치에서
  다시 단어 나무의 Root Node로부터 비교를 새로 시작

• 텍스트의 앞부분으로 다시 돌아가 비교

  • $O(m_sn)$

텍스트의 앞부분으로 되돌아가지 않는 방법?

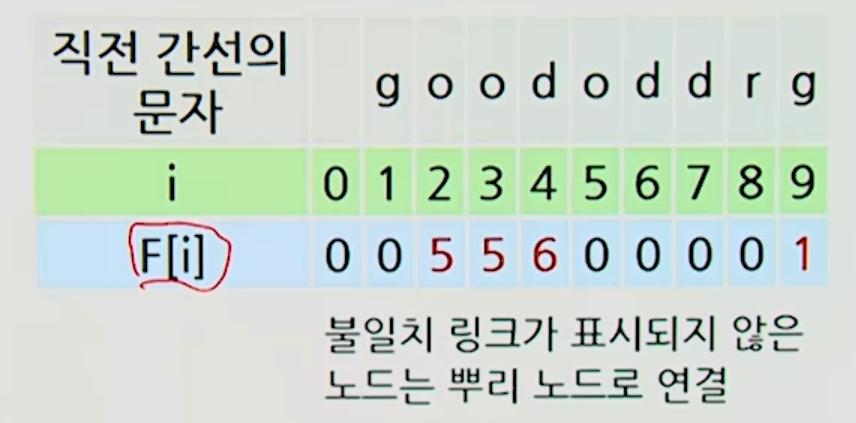
확장된 F 테이블("실패 함수") 사용

• $F[i]$ -> 단어 나무의 Node i에서 word(i)의 접미부와 최대로 일치하는
  임의의 패턴 $P_i$의 접두부에 해당하는 Node $F[i]$

  • 불일치 링크 -> Node i에서 노드 $F[i]$로 가는 간선

시간 복잡도

$O(\vert \sum \vert m_s + n)$ -> $\vert \sum \vert = 상수$ -> $O(m_s+n)$

• 각 Node에서 자식 노드로 분기할 때 알파벳 개수만큼의 배열을 이용한다고 가정

• 단어 나무 생성 -> $O(\vert \sum \vert m_s)$

  • 노드의 개수 $O(m_s)$ X 각 노드에서의 분기 개수 $\vert \sum \vert$

• 확장된 테이블 F 생성 -> $O(m_s)$

  • 단어 나무 생성 후 너비 우선 탐색을 이용

• 패턴 매칭 -> $O(n)$

  • 문자를 차례대로 읽으면서 단어 나무의 간선을 따라가다가
    일치하는 간선이 없으면 F 테이블을 따라가는 과정을 반복

2. 접미사 나무

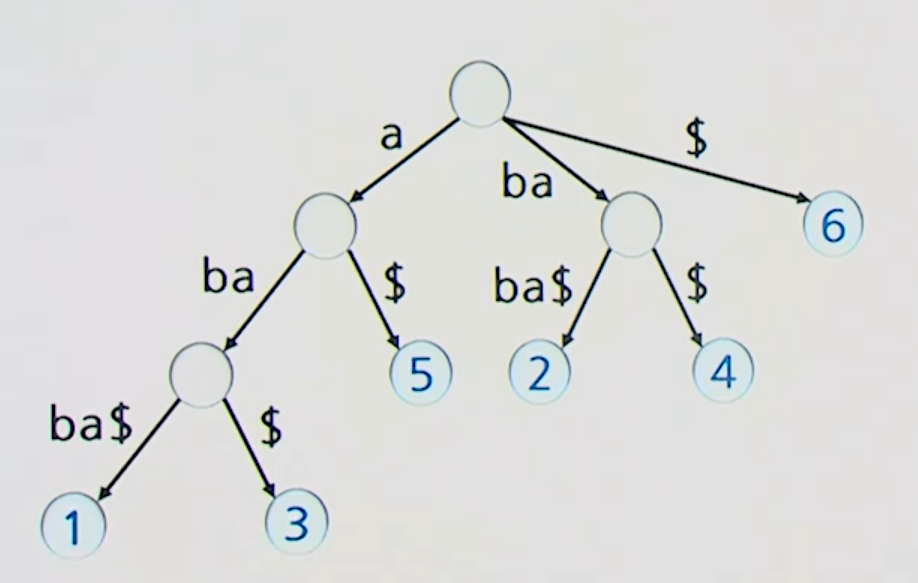
주어진 string의 모든 접미사를 표현하는 나무

인덱스 자료구조

다량의 데이터에 대한 접근을 빠르게 하기 위해 만드는 자료구조

• 문자열에 대한 인덱스 자료구조
  • 접미나 나무, 접미사 배열

• 각 edge는 하나 이상의 문자로 레이블 됨

• Root Node로부터 각 Leaf Node까지의 경로는 각각의 접미사에 해당

  • 해당 Leaf Node의 레이블은 접미사의 시작 위치를 표시

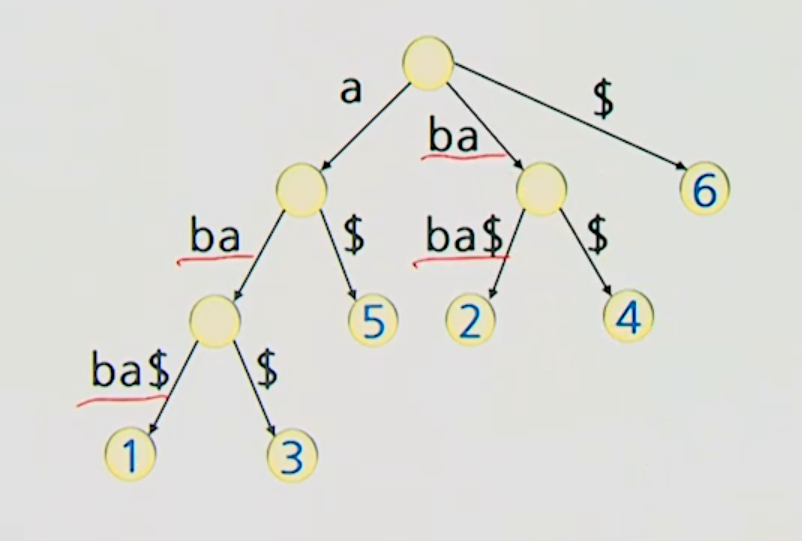
예제 $S = a b a b a$

접미사 나무 생성 알고리즘

Naive 알고리즘

• 모든 접미사로 이루어진 단어 나무 생성

  • 길이 1부터 n까지 하나씩 존재 -> 총 n개

• 단어 나무의 최대 노드 개수

  • $\displaystyle\sum_{i=1}^{n}i = \frac{n(n+1)}{2}$ -> $O(n^2)$

• 자식이 하나밖에 없는 Node를 지우고, 이 때 합쳐지는 두 간선의 레이블을 합친다.

  • Leaf Node n개, 내부 노드 n-1개 이하 -> 총 2n개 이하의 노드 -> $O(n)$

예시

1. 나무 생성
   

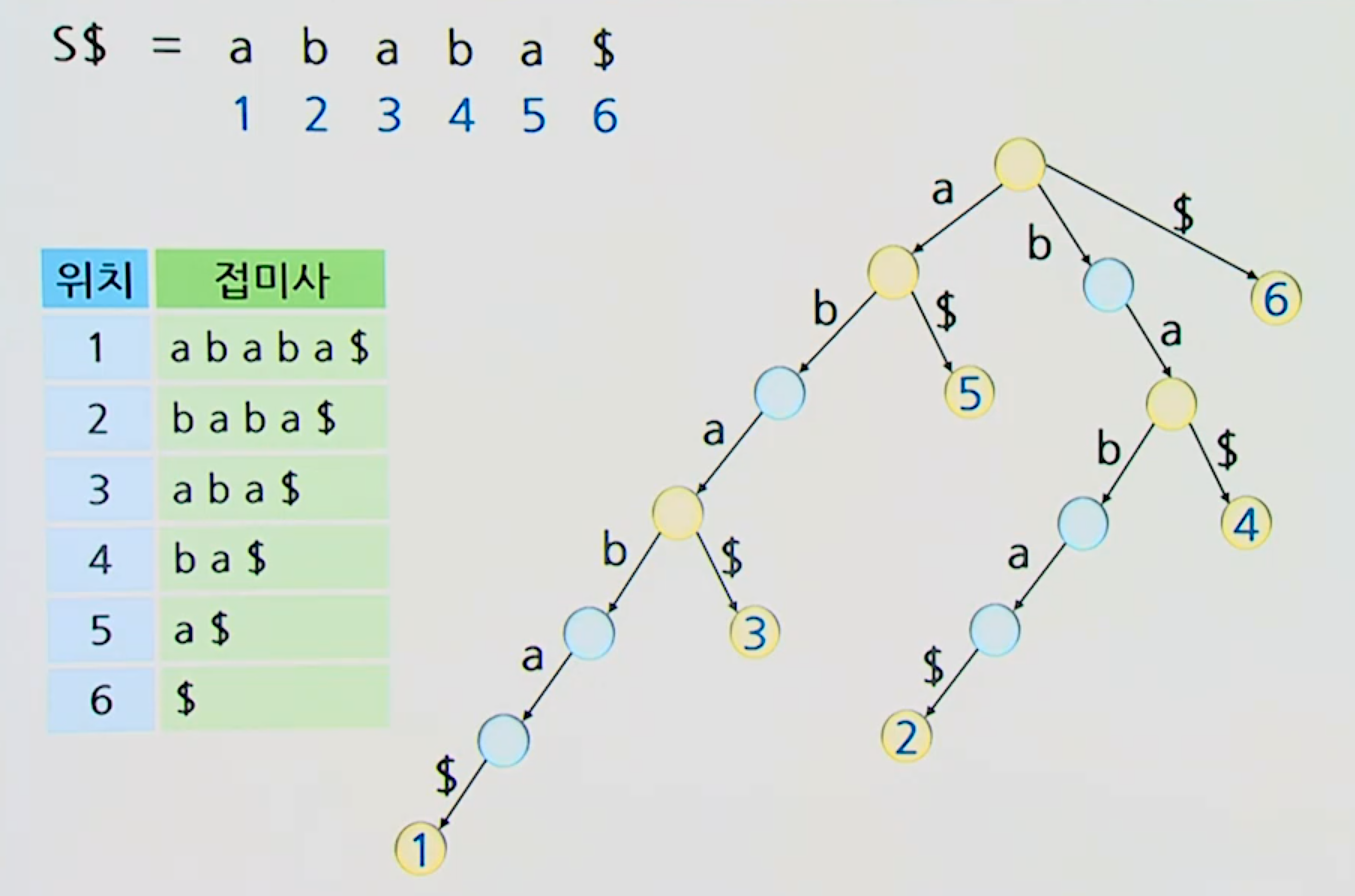
2. 하나만 있는 자식 제거
   

스트링 매칭 과정

1. 주어진 텍스트에 T에 대한 접미사 나무 생성
2. 찾고자 하는 패턴 P를 접미사 나무 Root node로부터 탐색
3. 만약 P를 찾았다면, 이 때 처음 만나는 Node v를 Root Node로 가지는
   부분 나무의 모든 Leaf Node를 찾으면 (깊이 우선 탐색)
   그 레이블이 T에서 P가 나타나는 모든 위치임.

시간 복잡도 : $O(m + occ)$

• 패턴의 길이 m

• 찾은 노드로부터 부분 나무의 모든 Leaf Node occ개를
  깊이 우선 탐색으로 찾는 시간 -> $O(occ)$