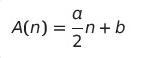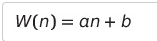1. 알고리즘 정의
(입출력) 0개 이상의 외부 입력, 1개 이상의 출력
(명확성) 각 단계는 모호하지 않고 단순 명확해야함
(유한성) 한정된 수의 작업 후에는 반드시 종료
(유효성) 모든 명령어는 수행 가능해야함.
- (실용적 관점) 효율적이어야 함.
2. 알고리즘 생성 단계
-
설계
-
표현 / 기술
- 일상 언어
- 순서도
- 의사코드
- 프로그래밍 언어
- etc...
-
정확성 검증 ( 분석 )
- 수학적 검증
- 실험 데이터
-
효율성 분석 ( 분석 )
- 공간 복잡도
- 시간 복잡도
3. 설계 기법
- Dynamic Programming
- 분할된 소문제들이 겹치는 부분을 가지고 있어, 이를 한 번만 계산할 수 있도록 하는 상향식 방법
- Divide and Conquer
- 문제를 더 작은 문제로 쪼갠 후, 각각의 해를 이용하여 전체 문제의 해를 찾는 하향식 방법
- Greedy
- 각 단계마다 최선이라고 여겨지는 선택을 통해 해를 찾는 방법
동적 프로그래밍과 분할정복의 공통점 및 차이점
공통점
- 문제를 작은 문제로 분할한다.
차이점
- 분할된 소문제들이 독립적이다. > 분할정복
- 분할된 소문제들이 중복이 있을 수 있다. > 동적 프로그래밍
4. 알고리즘 분석
정확성 분석
- 유효한 입력, 유한 시간 -> 정확한 결과를 생성
- 실무적 접근 > 테스트 데이터 활용
- 테스트 데이터는 일반성을 띄기 힘들거나 때에 따라 결과가 다를 수 있기 때문에
정확하지 않으므로, 좋은 방법이 아님.
- 테스트 데이터는 일반성을 띄기 힘들거나 때에 따라 결과가 다를 수 있기 때문에
- 학문적 접근 > 수학적 증명
- 수학적으로 논리 증명을 하기 때문에 Perfect하다.
- 실무적 접근 > 테스트 데이터 활용
효율성 분석
- 얼마나 빨리 수행하는가?
- 시간 복잡도
- 얼마나 많은 메모리를 차지하는가?
- 공간 복잡도
5. 시간 복잡도
컴퓨터에서 시간을 측정하는 방법
- 컴퓨팅 스펙, 프로그래밍 언어 및 프로그램이 작성 방법, 컴파일러 효율성 등에 종속적이다.
- 즉, 일반성이 결여되기 때문에 위 방법으로 측정하면 안된다.
그래서 아래의 방법으로 측정한다.
각 명령문의 수행 횟수의 합
- 가정 > 각 명령문의 수행 시간을 모두 동일
- 시간 복잡도에 영향을 미치는 요인
- 입력 크기 n
- 입력 데이터의 상태
입력 데이터의 상태에 따라 달라짐.
Sn : 크기가 n인 입력들의 집합
P(I) : 입력 I가 발생할 확률
t(I): 입력 I일 때의 수행 시간
평균 수행 시간
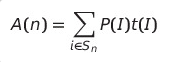
최선 수행 시간

최악 수행 시간
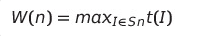
시간 복잡도는 최악 수행 시간을 기준으로 한다.
6. 시간복잡도 예시
순차 탐색 알고리즘의 수행시간 계산 ( Example )
- 입력
- A[0,.... n-1]
- n: 데이터 개수
- x: 탐색 키
def search_sequential(a: list, n, x):
i = 0 # c1 > 1번 수행
while a[i] != x: # c2 > k번 수행
i += 1 # c3 > k-1번 수행
return i # c4 1번 수행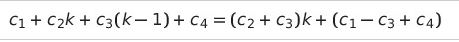
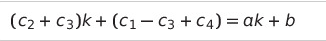
평균 수행 시간
- k = 2 / n
최악 수행 시간
- k = n
상수 * n + 상수
-
n을 무한대로 보내면, 상수항 보다 n의 차수가 더 중요하다.
- 다항식 수행 시간에서 최고 차수에 의해 결정.
- 최고 차수가 낮은 다항식이 더 빠른 시간에 결과를 생성한다.
-
상수의 정확한 값은 컴퓨터의 성능이나 최적화에 따라 달라지므로 계산이 곤란.
- 시간 복잡도는 주로 수행 시간의 차수를 이용하여 표현.
- 명령줄마다 부여한 상이한 수행시간은 의미가 없음.
7. 점근 성능
입력 크기 n이 충분히 커짐에 따라 결정되는 성능
- 수행 시간의 다항식 함수에서 최고 차수에 의해 결정
- 낮은 차수의 항이나 계수 및 상수항은 무시
- 그렇기 때문에 어림값이다. ( 정확하지 않다 )
- 수행 시간의 증가 추세 파악에 용이하고, 알고리즘 우열 판단의 기준이 된다.
- 낮은 차수의 항이나 계수 및 상수항은 무시
표기법
-
점근적 상한 ( Big-Oh )
-
점근적 하한 ( Big-Omega )
-
점근적 상하한 ( Big-Theta )
Big-Oh ( 점근적 상한 )
- 어떤 양수 c와 n0이 존재하여, 모든 n >= n0에 대해,
f(n) <= cg(n)을 만족하면, f(n) = O(g(n)) 이다.
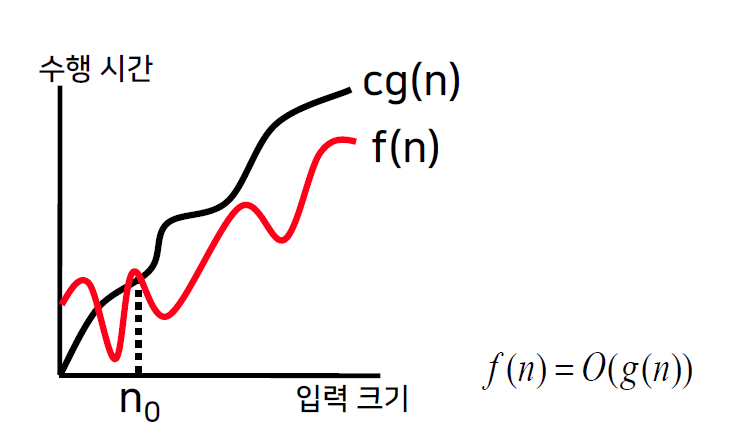
- cg(n)이 상한이기 때문에, 아무리 오래 걸려도 cg(n)보다는 오래걸리지 않을 것이다.
Big-Omega ( 점근적 하한 )
- 어떤 양수 c와 n0이 존재하여, 모든 n >= n0에 대해,
f(n) >= cg(n)을 만족하면, f(n) = Omega(g(n)) 이다.
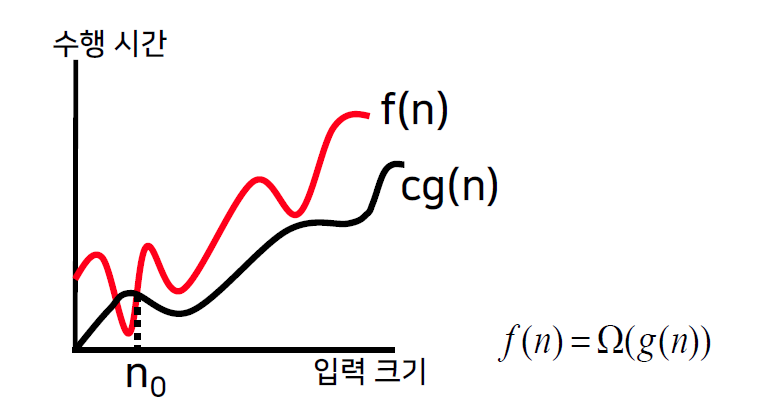
- cg(n)이 하한이기 때문에, 아무리 빨라도 cg(n)보다는 빠를 수 없다.
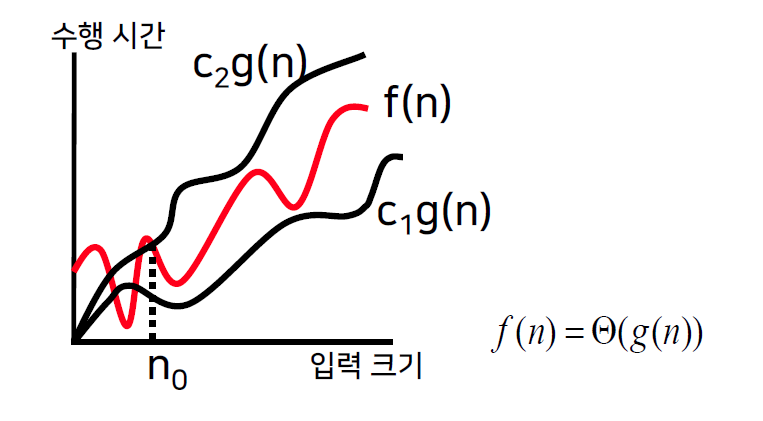
Big-Theta ( 점근적 상하한 )
- 양의 상수 c1, c2와 n0가 존재하여 모든 n≥n0에 대해 c1g(n) ≤ f(n) ≤ c2g(n)이면,
f(n)=Θ(g(n))이다.
최고 차수, 최소 차수
Big-Oh
- 점근적 상한이기 때문에, g(n)이 무한이 클 수 있다.
- 그래서 빅오는 g(n)의 경우의 수 중 최소 차수를 기준으로 한다.
Big-Omega
- 점근적 하한이기 때문에, g(n)이 무한이 작을 수 있다.
- 그래서 빅오메가는 g(n)의 경우의 수 중 최고 차수를 기준으로 한다.
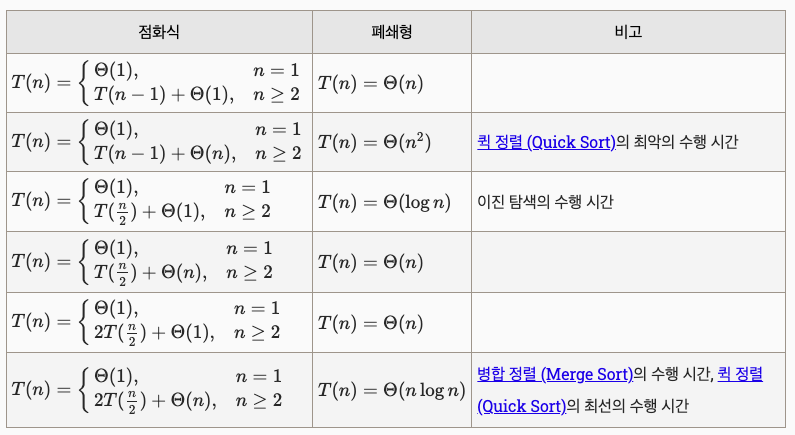
8. 순환 알고리즘의 성능 - 점화식과 폐쇄형
자기 자신의 알고리즘을 다시 수행하는 형태의 순환(Recursion, 재귀) 알고리즘의 성능은
지금까지의 방법으로 구할 수 없고 일반적으로 점화식을 유도하고 점화식의 폐쇄형을 구해서 계산한다.

- 이진 탐색 알고리즘 점화식 유도

- 점화식의 폐쇄형 구하기
기본 점화식과 폐쇄형