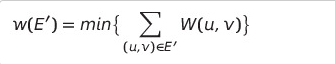개요
주어진 문제의 해를 구하는 일련의 선택 단계마다 전후 단계의 선택과는 무관하게
해당 단계에서 가장 최선이라고 볼 수 있는 선택을 통해 전체적인 최적해를 찾는 설계기법
특징
- 국부적인 최적해 ( 로컬 해 )가 전체의 최적해를 이끈다.
- 최적성의 원리를 만족.
문제의 크기를 줄인 소문제의 해들을 합치면 전체 문제의 해가 된다.동전 문제
고객에게 돌려줄 거스름 돈이 T만큼 있을 때,
고객이 받을 동전의 개수를 최소로 하면서 거스름돈을 돌려주는 방법을 찾는 문제.
기본 아이디어
거스름돈의 액수를 초과하지 않는 조건하에서
단순히 액면가가 큰 동전부터 최대한 사용
동전의 액면가가 정해진 경우
-
동전의 종류 C[i] = { 500, 100, 50, 10 }
-
T : 고객에게 돌려줄 거스름돈
-
n : 동전의 종류
-
C[i] : i번째 동전의 액면가 ( 1 <= i <= n )
-
X[i] : 거스름돈에서 사용한 i번째 동전
Greedy_Coin (T, n, C, X)
{
for ( i=1; i<=n; i++){
X[i] = T/C[i];
T = T - C[i] * X[i];
}
}
시간복잡도 O(n)동전의 액면가가 임의로 주어지는 경우
- T = 150원
- 동전의 종류 C[i] = { 500, 120, 100, 50, 10 }
욕심쟁이 방법
120 + 10 + 10 + 10
실제 최적해
100 + 50
일반적인 경우의 동전 문제는 욕심쟁이 방법을 적용할 수 없다.
배낭문제
최대 용량 M인 하나의 배낭과 n개의 물체
- 각 물제 i에는 물체의 무게 w(i)와 이익 p(i)가 있다.
기본 아이디어
배낭의 용량을 초과하지 않는 범위 내에서
배낭에 들어있는 물체의 이익의 합이 최대로 되는 해를 찾는 문제
- 단위 무게당 이익이 가장 큰 물체부터 차례대로 배낭에 최대한 넣는 과정을 반복
물체를 쪼갤 수 있을 때
- 용량 M : 10kg
- 물체 1: 핫도그 무게 4kg, 이익 16
- 물체 2: 초콜릿 무게 2kg, 이익 4
- 물체 3: 바나나 무게 4kg, 이익 12
- 물체 4: 도넛 무게 3kg, 이익 15

- 단위 무게당 이익
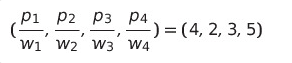
진행 방식
-
- 도넛을 넣는다. ( 남은 용량 7 )
-
- 핫도그를 넣는다. ( 남은 용량 3 )
-
- 바나나를 남은 용량만큼 쪼개서 넣는다. ( 남은 용량 0 ) -> 12 * 3/4
-
최대 이익: 40
- p[i], w[i] = 물체 i의 이익과 무게 ( 1 <= i <= n )
- 단위 무게당 이익이 감소순으로 정렬 ( O(nlogn) )
- n, M = 각각 물체의 개수와 배낭의 용량
- X[i] = 배낭에 들어간 물체 i의 비율
Kanpsack (p, w, M, n, X)
{
for (i=1; i<=n; i++) x[i] = 0; # 초기화, O(n)
r = M;
for (i=1; i<=n; i++){
if (w[i] <= r) {
x[i] = 1;
r = r -w[i];
}
else break;
} # O(n)
if (i <= n) x[i] = r / w[i]; # 남은 배낭 용량보다 물체 용량이 크면, 물체를 쪼갠다.
}물체를 쪼갤 수 없을 때 ( 0 / 1 배낭 문제 )
- M = 10
- n = 4
- (p1, p2, p3, p4) = (16, 4, 12, 15)
- (w1, w2, w3, w4) = (4, 2, 4, 3)
- 단위 무게당 이익 = (4, 2, 3, 5)
욕심쟁이 방법
p4 + p1 = 31
실제 최대 이익
p4 + p1 + p2 = 45
0 / 1 배낭문제에는 욕심쟁이 방법을 적용할 수 없다.
작업 스케쥴링 문제
최소 개수의 기계를 사용해서 작업 간의 충돌이 일어나지 않도록
모든 작업을 기계에 할당하는 문제
- 작업의 집합

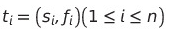
s(i) : 작업의 시작시간
f(i) : 작업의 종료시간
- 작업이 시작되면 중단없이 기계에서 완료
- 작업 간 충돌 불가
- 충돌 -> 한 기계에서 동시에 두 개 이상의 작업 수행
- 충돌을 피하기 위한 조건
- f(i) <= s(j) 또는 f(j) <= s(i)
기본 아이디어
각 단계에서 시작 시간이 빠른 작업을 우선적으로 선택
- 충돌이 발생하지 않으면 해당 기계에 할당
- 충돌이 발생하면 새로운 기계에 할당
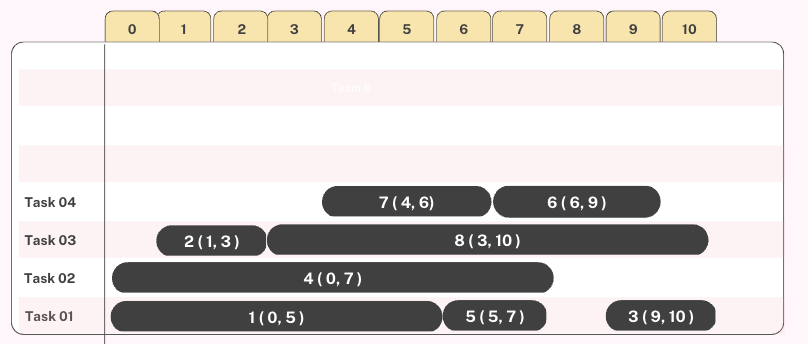
실행방식
- t1 = (0, 5)
- t2 = (1, 3)
- t3 = (9, 10)
- t4 = (0, 7)
- t5 = (5, 7)
- t6 = (6, 9)
- t7 = (4, 6)
- t8 = (3, 10)
시작시간이 빠른 작업을 우선적으로 처리
- 시작시간의 오름차순 정렬
- t1 = (0, 5)
- t4 = (0, 7)
- t2 = (1, 3)
- t8 = (3, 10)
- t7 = (4, 6)
- t5 = (5, 7)
- t6 = (6, 9)
- t3 = (9, 10)
최소 4개의 기계가 필요
- T[1,2, ..., n][1..2]
- T[i][1] : 작업 i의 시작시간
- T[i][2] : 작업 i의 종료시간
- n : 작업의 개수
- m : 필요한 최소 기계의 수
TaskScheduling (T, n) {
T를 시작 시간으로 오름차순 정렬; # O(nlogn)
m = 1;
for (i=1; i<=n; i++) { # O(n)
if (작업 t_i를 수행할 기계 p(1<=p<=m)가 있으면) { # O(logn)
작업 t_i를 기계 p에 할당;
} else {
m = m + 1;
작업 t_i를 새 기계 m에 할당;
}
}
return m;
}- T를 시작 시간으로 오름차순 정렬
- O(nlogn)
- for (i=1; i<=n; i++)
- O(n)
- 작업 t_i를 수행할 기계 p(1<=p<=m)가 있으면
- O(logn)
- 최종 시간 복잡도
- O(nlogn)
작업 선택 문제
하나의 기계를 사용해서 충돌없이 최대 개수의 작업을 기계에 할당하는 문제
- 작업 스케쥴링과 유사
기본 아이디어
각 단계에서 완료시간이 빠른 작업을 우선적으로 선택
- 충돌이 발생하지 않으면 기계에 할당
- 충돌이 발생하면 작업을 버림
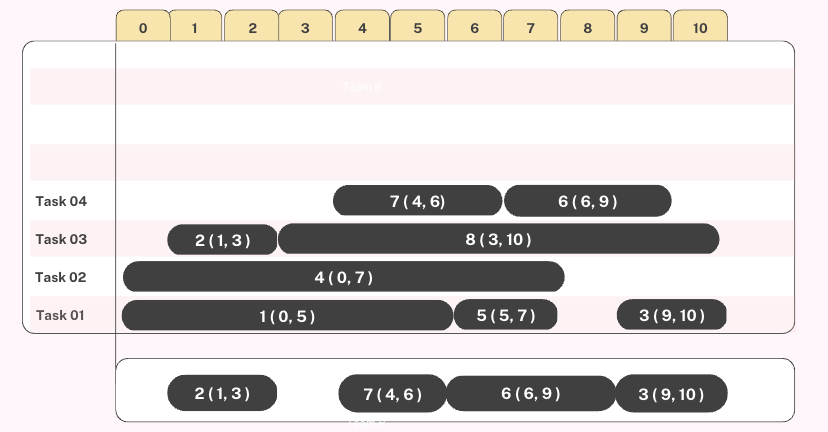
실행방식
- t1 = (0, 5)
- t2 = (1, 3)
- t3 = (9, 10)
- t4 = (0, 7)
- t5 = (5, 7)
- t6 = (6, 9)
- t7 = (4, 6)
- t8 = (3, 10)
완료시간이 빠른 작업을 우선적으로 처리
- 완료시간의 오름차순 정렬
- t2 = (1, 3)
- t1 = (0, 5)
- t7 = (4, 6)
- t4 = (0, 7)
- t5 = (5, 7)
- t6 = (6, 9)
- t8 = (3, 10)
- t3 = (9, 10)
최대 4개의 작업 처리 가능
- T[1,2, ..., n][1..2]
- T[i][1] : 작업 i의 시작시간
- T[i][2] : 작업 i의 종료시간
- n : 작업의 개수
- m : 최대 작업의 수
ActivitySelection (T, n) {
작업을 완료 시간의 오름차순 정렬; # O(nlogn)
m = 0;
for (i=1; i<=n; i++) { # O(n)
if (작업 t_i가 충돌을 일으키지 않으면) { # O(1)
m = m + 1;
작업 t_i를 기계에 할당;
}
}
return m;
}최소 신장 트리
신장 트리란?
가중 무방향 그래프에서 모든 정점들을 포함하는 연결된 부분 그래프 중 트리인 것
최소 신장 트리란?
간선 (u, v)마다 가중치 w(u, v)를 가진
연결된 무방향 그래프 G = (V, E)에 대하여 다음을 만족하는
트리 G' = (V, E')
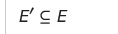
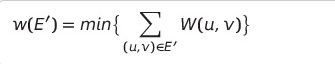
- 신장 트리 중에서 간선 가중치의 합이 가장 작은 트리
욕심쟁이 방법을 적용한 알고리즘 2개
Kruskal, Prim
- 두 알고리즘의 뼈대
Greedy-MST (G = (V,E)) {
T <- ∅; # 공집합으로 초기화
while (T가 신장트리를 만들지 않음) {
최선의 간선 (u, v)를 선택;
T <- T U { (u, v) };
}
return T;
}- 최선의 간선이란?
- 사이클을 형성하지 않으며
- 최소의 가중치를 갖는 간선
- 최선의 간선을 선택하는 방법에 따라 Kruskal과 Prim으로 나뉜다.
Kruskal 알고리즘
간선이 하나도 없는 상태에서 시작하여,
가중치가 가장 작은 간선부터 하나씩 선택하여
싸이클을 만들지 않는 간선을 추가하는 방법.
- 싸이클을 만들지 않는 간선
- 서로 다른 연결 성분에 속하는 정점을 잇는 간선
- n개의 정점이 다른 연결 성분으로 구성된 상태에서 시작하여
간선이 추가될 때마다 연결 성분들이 합쳐지고
최종적으로 하나의 연결 성분을 형성
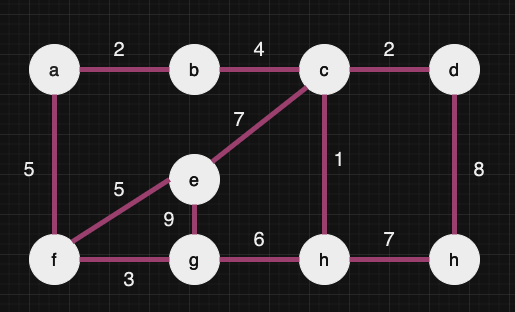
간선을 제거한 후 모두 다른 연결 성분이 상태로 초기화

간선을 가중치로 정렬
- c ---- h
- a ------- b
- c ------- d
- f --------- g
- b ----------- c
- e ------------- f
- a ------------- f
- g --------------- h
- c ----------------- e
- h ----------------- i
- d -------------------- i
- e ----------------------- g
간선을 차례대로 연결성분에 잇는다.
- 연결 성분이 간선으로 이어질 때마다
연결된 성분들은 하나로 인식한다.
- 동일한 연결 성분끼리 잇는 간선을 제외하고 모두 간선을 연결한다.
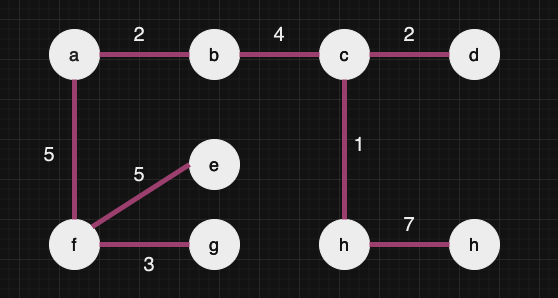
- 가중치의 합 : 29
G : 그래프 G = (V, E)의 인접 리스트
T: 최소 신장 트리의 간선 집합 T
Kruskal (G, T) {
T = ∅;
for (각 정점 v에 대해) {
정점 v로 구성된 연결 성분 초기화;
가중치가 증가하는 순으로 모든 간선 E 정렬;
}
for (가중치가 가장 작은 간선부터 모든 간선 (u,v) in E에 대해) {
if (u와 v가 다른 연결 성분에 있으면) {
T = T U { (u, v) };
u의 연결 성분과 v의 연결 성분을 합침;
}
else 간선 (u, v)를 버림;
}
return T;
}시간 복잡도
- for (각 정점 v에 대해) {
- O(|V|)
- 가중치가 증가하는 순으로 모든 간선 E 정렬;
- O(|E| log |E|)
- 가중치가 가장 작은 간선부터 모든 간선 (u,v) in E에 대해;
- O(|E| * α (|E|, |V|))
- 상수 취급한다.
가중치가 증가하는 순으로 모든 간선 E 정렬하는 부분이 가장 중요.
- O(|E| log |E|)
Prim 알고리즘
임의의 한 정점으로부터 시작하여, 연결된 정점을 선택해서 추가하는 방법.
- 이미 선택된 정점의 집합 S와 미선택 정점의 집합 V-S를 잇는 간선 중,
가중치가 가장 작은 간선을 선택
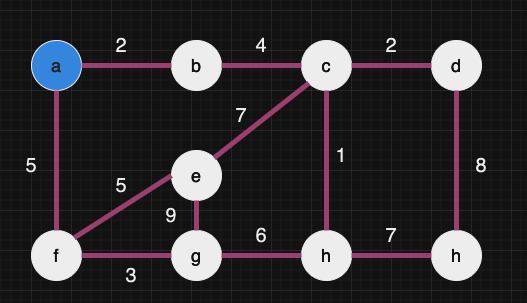
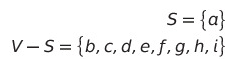
a 정점에서 직접적으로 연결된 간선 중 가중치가 작은 간선을 선택
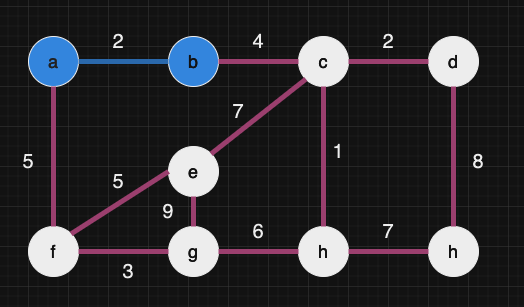
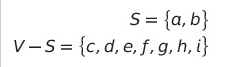
a와 b정점에서 직접적으로 연결된 모든 간선 중 가중치가 작은 간선을 선택

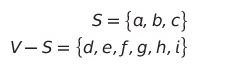
a, b, c정점에서 직접적으로 연결된 간선 중 가중치가 작은 간선을 선택
- 반복하면 된다.


G : 그래프 G = (V, E)의 인접 리스트
T: 최소 신장 트리의 간선 집합 T
Prim (G, T) {
T = ∅;
S = { a }; // 임의의 정점
while ( S != V) {
u in S, v in V-S인 것 중 가중치가 최소인 간선 (u,v) 선택;
T = T U { (u, v) };
S = S U { v };
}
return T;
}시간 복잡도
- 인접 행렬
- O(|V|^2)
- 인접 리스트 + 힙
- O( (|V| + |E|) log|V| )