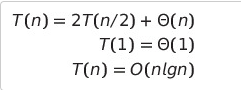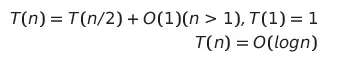1. 개념
순환적으로 문제를 푸는 하향식 (Top - Down)설계 방법
- 분할된 작은 문제들의 각 해를 구하고, 해를 결합하여 원래의 문제의 해를 구함
특징
- 분할된 소문제는 원래 문제와 동일
- 단, 입력 크기만 작아짐
- 단, 입력 크기만 작아짐
- 분할된 작은 문제는 독립적
- 순환적 분할 및 결과의 결합이 가능
처리 단계
분할
주어진 문제를 여러개의 소문제로 분할
정복
소문제들을 순환적으로 분할.
- 더 이상 분할되지 않을 정도로 충분히 작다면, 순환 호출 없이 소문제의 해를 구함
결합
소문제에 대해 정복된 해를 결합하여 원래 문제의 해를 구함
- 일부 알고리즘의 경우, 결합 과정이 없는 케이스도 존재
2. 이진 탐색
정렬된 상태의 데이터에 대한 효과적 탐색 방법
- 오름차순으로 정렬되어 있다고 가정
탐색 과정
- 배열의 가운데 원소와 탐색키 x를 비교
- 탐색키 = 가운데 원소
- 탐색 성공
- 탐색 성공
- 탐색키 < 가운데 원소
- 이진탐색 ( 크기 1/2의 왼쪽 부분배열) 순환 호출
- 이진탐색 ( 크기 1/2의 왼쪽 부분배열) 순환 호출
- 탐색키 > 가운데 원소
- 이진탐색 ( 크기 1/2의 오른쪽 부분배열) 순환 호출
- 탐색키 = 가운데 원소
분할
- 배열을 가운데 원소를 기준으로 왼쪽, 오른쪽 부분배열 분할.
정복
- 탐색키가 가운데 원소보다 작으면, 왼쪽 부분배열을 대상으로 순환 호출
- 탐색키가 가운데 원소보다 크면, 오른쪽 부분배열을 대상으로 순환 호출
결합
- 부분배열에 대한 탐색 결과를 직접 반환 -> 결합 X
// Pseudo code
BinarySearch(A[], Left, Right, x){
if (Left > Right) return -1; // 탐색 실패
Mid = (Left + Right) / 2;
if (x == A[Mid]) return Mid;
else if (x < Mid)
BinarySearch(A, Left, Mid-1, x); // 왼쪽 부분배열
else
BinarySearch(A, Mid+1, Right, x); // 오른쪽 부분배열
}성능
- T(n) = 입력크기 n에 대한 모든 비교 횟수의 합 = 맨 바깥 수준에서의 비교 횟수 + 순환 호출에서의 비교 횟수
3. 퀵 정렬
특정 원소를 기준으로 기준 배열을 두 부분배열로 분할하고,
각 부분배열에 대해서 퀵 정렬을 순환적으로 적용
- 분할 원소 (피벗)
- 두 부분배열로 분할할 때, 기준이 되는 원소
- 보통 주어진 배열의 첫 번째 원소로 지정
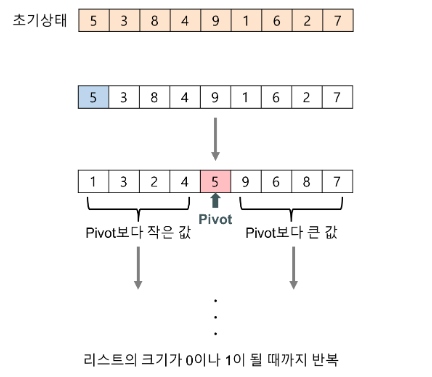
원리
분할원소가 제자리를 잡도록 하여 정렬하는 방식
분할
- 분할 원소를 기준으로 주어진 배열을 두 부분배열로 분할
정복
- 두 부분배열에 대해 퀵 정렬을 순환적으로 적용하여 각 부분배열을 정렬
결합
- 결합 없음
// Pseudo code
QuickSort(A[], n){
if (n > 1) {
// 분할 원소를 기준으로 두 부분배열로 분할
pivot = Patrition(A[0...n-1], n);
// 왼쪽 부분배열에 대한 순환호출
QuickSort(A[0...pivot-1], pivot);
// 오른쪽 부분배열에 대한 순환호출
QuickSort(A[pivot+1...n], n-pivot-1);
}
}
int Partition(A[], n){
Left = 1; Right = n-1;
while (Left < Right) { // 분할 원소 A[0]
// 분할원소보다 큰 값의 위치를 찾음
while (Left < n && A[Left] < A[0]) Left++;
// 분할원소보다 작은 값의 위치를 찾음
while (Right > 0 && A[Right] >= A[0]) Right++;
// 분할원소 이동
if (Left < Right) 교환(A[Left] <-> A[Right]
else 교환(A[0] <-> A[Right)
}
return Right;
}성능
-
Partition 함수
- 분할 원소를 제외한 모든 원소가
분할원소와 한 번 또는 두 번(위치가 교환되는 원소의 경우)의 비교 수행
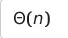
- 분할 원소를 제외한 모든 원소가
-
최악 수행 시간
- 분할 원소를 제외한 나머지 모든 원소가 하나의 부분배열이 되는 경우
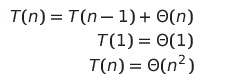
- 분할 원소를 제외한 나머지 모든 원소가 하나의 부분배열이 되는 경우
- 최선 수행 시간
- 분할원소를 중심으로 동일한 크기의 두 부분배열로 나뉘는 경우
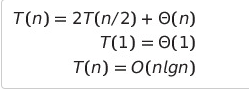
- 분할원소를 중심으로 동일한 크기의 두 부분배열로 나뉘는 경우
- 평균 수행 시간
- 분할 원소가 분할 후에 배열의 어느 곳에나 동일한 확률로 위치하는 것이 가능
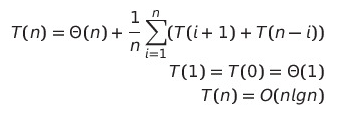
- 분할 원소가 분할 후에 배열의 어느 곳에나 동일한 확률로 위치하는 것이 가능
특징
- 이미 정렬되어있고 맨 앞에 원소를 pivot으로 정한 경우 최악의 수행시간을 갖는다.
- 분할원소 선택의 임의성만 보장되면
- 평균 성능을 보일 가능성이 높다.
- 배열에서 임의의 원소를 선택해서 배열의 처음 원소와 서로 교환 후 퀵 정렬 수행
- 평균 성능을 보일 가능성이 높다.
- 안정적이지 않음
- 동일한 키 값을 갖는 원소들의 정렬 전의 상대적인 위치가
정렬 후에 그대로 유지된다는 보장을 못한다.
- 동일한 키 값을 갖는 원소들의 정렬 전의 상대적인 위치가
4. 합병 정렬
배열을 동일한 크기의 두 부분 배열로 분할하고,
각각의 부분 배열을 순환적으로 정렬한 후,
정렬된 두 부분배열을 합병하여 하나의 정렬된 배열을 만드는 방식
분할
- 입력 크기가 n인 배열을 n / 2개의 원소를 가진 두 부분배열로 분할
정복
- 각각의 부분 배열에 대해 합병정렬을 순환적으로 적용하여 정렬
결합
- 정렬된 두 부분배열을 합병하여 하나의 정렬된 배열을 만듦
# Pseucode
MergeSort(A[], n) {
if (n > 1) {
Mid = n/2;
B[0...Mid-1] = MergeSort(A[0...Mid-1], Mid); // 왼쪽
C[0...n-Mid-1] = MergeSort(A[Mid....n-1], n-Mid); // 오른쪽
// 합병
A[0...n-1] = Merge(B[0...Mid-1), C[0...n-Mid-1], Mid, n-Mid);
}
}
Merge(B[], C[], n, m){
i = j = k = 0;
while (i < n && j < m) {
if (B[i] <= C[j])
// B[i]를 선택 후 i를 1증가
A[k++] = B[i++];
else
// C[j]를 선택 후 j를 1증가
A[k++] = C[j++]
}
for (; i<n; i++) A[k++] = B[i]; // 남은 원소 이동
for (; i<n; i++) A[k++] = C[j]; // 남은 원소 이동
return A[0....n+m-1];
}성능
-
Merge() 함수
- B[n/2] + C[n/2] -> A[n]
- 두 부분배열 간의 비교 횟수 : n/2 ~ n-1

- 두 부분배열 간의 비교 횟수 : n/2 ~ n-1
- B[n/2] + C[n/2] -> A[n]
-
합병 정렬 수행 시간
- 크기 n/2의 두번 순환 호출 + 한 번의 합병
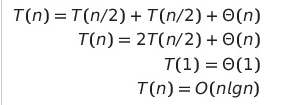
- 크기 n/2의 두번 순환 호출 + 한 번의 합병
5. 선택 문제
n개의 원소가 임의의 순서로 저장된 배열에서 i번째로 작은 원소를 찾은 문제
- i=1 -> 최소값,
- i = n/2 -> 중간값,
- i=n -> 최대값
직관적인 방법
- 오름차순 정렬 후 i번째 원소 찾기
- O(nlgn)
- O(nlgn)
- 최소값을 찾는 과정을 i번 반복
- i-1번째까지는 최소값을 찾은 후 삭제
- O(in)
- O(in)
- i-1번째까지는 최소값을 찾은 후 삭제
- 최악의 경우 O(n^2)
- 평균 O(n)
- 평균 O(n)
- 최선의 경우 O(n)
- 평균 O(n)
- 평균 O(n)
최악 O(n^2), 평균 O(n) 시간 알고리즘
개념과 원리
퀵정렬의 Partition() 함수를 순환적용
// Pseudo code
int Selection(A[], n, i){
Left = 0; Right = n-1;
j = Partition(A, n);
if (i == j+1) return A[j]; // i번째 최소값
else if (i < j + 1)
Selection(A[Left...j-1], (j-1)-Left+1, i); // 왼쪽 부분 배열
else
Selection(A[j+1...Right], Right-(j+1)+1, i-(j+1); // 오른쪽 부분 배열
}성능
- 최악
- 퀵 정렬의 최악과 동일
- 데이터가 오름차순으로 정렬된 상태에서 i=n을 찾는 경우
- 퀵 정렬의 최악과 동일
최악의 성능을 피하는 해결책
항상 일정한 비율의 두 부분배열로 분할
- 최악 O(n)
- 아래에 설명할 거임
최악 O(n), 평균 O(n) 시간 알고리즘
개념과 원리
특정한 성질을 만족하는 원소를 분할원소로 선택
- 항상 일정한 비율의 두 부분배열로 분할
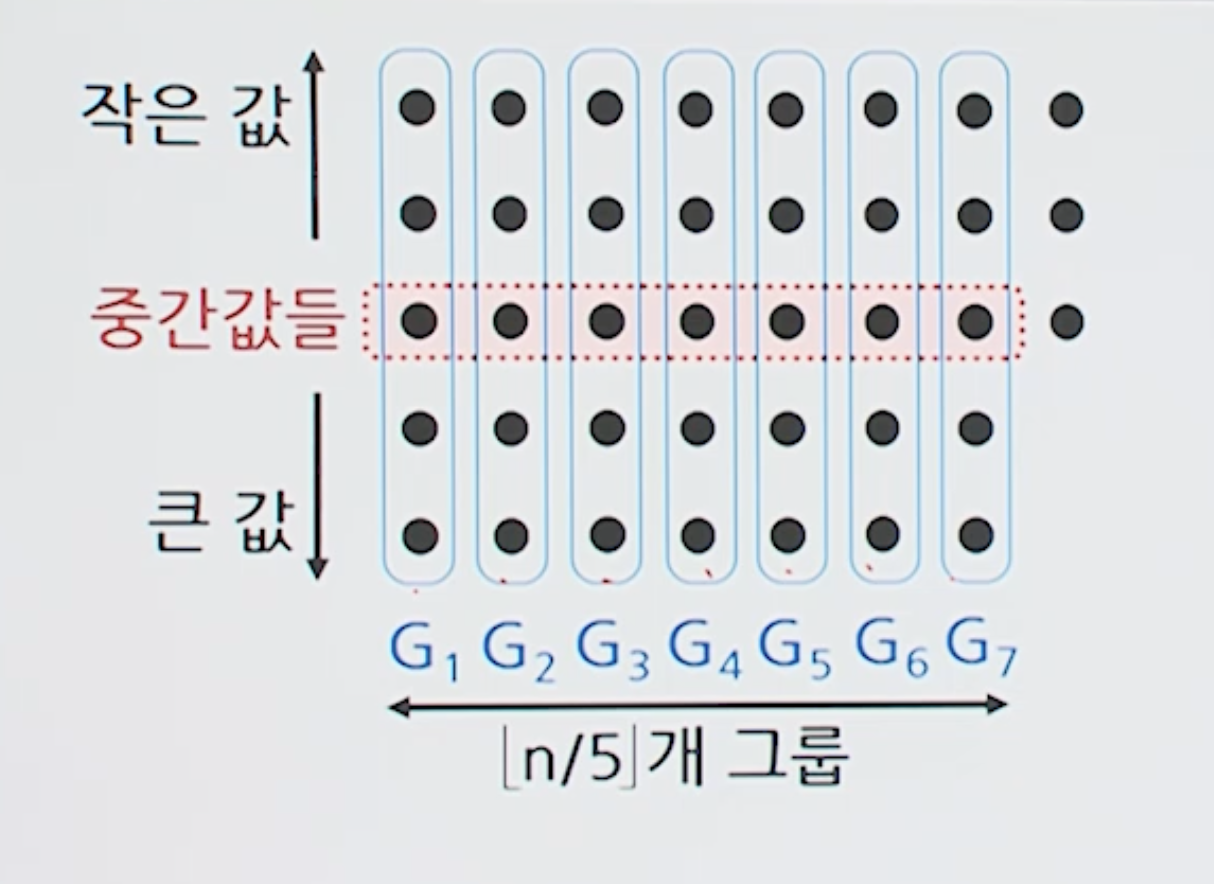
분할 원소 선택 방법
- 크기 n인 배열의 원소를 5개씩 묶어 n/5개의 그룹을 만듦
- 그룹을 형성하지 못한 채 남는 원소는 그대로 남김 (분할 원소 선택에서 제외)
- 그룹을 형성하지 못한 채 남는 원소는 그대로 남김 (분할 원소 선택에서 제외)
- 각 그룹의 원소들에 대해서 중간값을 찾음
- n/5개의 중간값들을 대상으로 다시 중간값을 찾음
- 중간값들의 중간값 -> 분할 원소
부분배열로의 분할 비율
- 분할할 때마다, 탐색 대상에서 제외되는 원소의 수는 몇개인가?
// Pseudo code
int Selection_n(A[], n, i) {
[단계 1] if (n < 5) 배열 A에서 i번째 원소를 찾아서 반환
else [단계 2] ~ [단계 6] 진행
[단계 2] A의 원소를 5개씩 묶어서 n/5개의 그룹 생성
[단계 3] 각 그룹의 중간 값을 구하고, 이들을 모다 배열 M을 구성
[단계 4] 중간값들의 중간값을 계산하기 위해 선택함수를 순환 적용 // 분할 원소의 인덱스 -> j
p = Selection_n(M, n/5, n/5/2)
[단계 5] p를 분할 원소로 사용하여 A를 분할
[단계 6] if ( i == j + 1) return A[j]
else if (i < j + 1) Selection_n(A[0...j-1], j, i) // 순환 호출
else Selection_n(A[j+1...n-1], n-j-1, i-j-1) // 순환 호출
}6. 최근접 점쌍 찾기
2차원 평면상에 있는 n개의 점들 중에서
서로의 거리가 가장 가까운 두 점을 찾는 문제
- O(n^2) -> 분할 정복을 적용하면 O(nlogn)
분할
- 점집합 S를 n/2개의 점들로 구성된 두 부분집합으로 분할
정복
- 분할된 두 부붅비합에 최근접 점쌍 알고리즘을 순환호출하여 정복
결합
- 두 부분집합 사이의 최근접 점쌍을 구하여, 이것과 각 부붅비합 내외 최근점 점쌍 중에서
최소 거리인 것을 S내에서의 최근점 점쌍으로 취함
// Pseudo code
int CPP(S[], n){
// 입력 S[0...n-1] -> 입력 점집합
// n -> 집합 S의 원소 개수
// 출력 -> 최근접 점쌍 간의 거리
[단계 0] 점집합 S를 x좌표의 오름차순으로 정렬하여 S_x를 구하고,
y좌표의 오름차순으로 정렬한 S_y를 구 // O(nlogn)
[단계 1] S를 이등분하는 수직선 l를 긋고,
이것의 좌측의 점 S_l과 우측의 점집합 S_r을 구함 // O(n)
[단계 2] S_l의 최근접 점쌍을 순환적으로 구한다.
구한 거리를 d_l이라고 함. // T(n/2)
[단계 3] S_r의 최근접 점쌍을 순환적으로 구한다.
구한 거리를 d_r이라고 함. // T(n/2)
[단계 4] 결합
d = mid{d_l, d_r}
// S_y`을 S_y에서 수직선 l을 중심으로 +-d 이내에 있는 점만으로 정의
// O(n)
for ( i in S_y`)
for (j = i+1; j<=i+7; j++)
if (점 i와 점 j의 y좌표 차이가 d 이상) break;
else if (점 i와 점 j의 거리가 d보다 작으면)
d를 점 i와 점 j의 거리로 바꿈;
return d;
}