[알고리즘 9강] 스트링 매칭

1. 개념

텍스트에서 패턴이 나타나는 모든 위치를 찾아내는 문제

• 텍스트 $T[0..n-1]$, 패턴 $P[0...m-1]$, $n > m$
  • 알파벳 $\sum$ -> 문자의 집합
  • 스트링 (문자열) -> 문자가 연속적으로 나열된 것

패턴을 전처리하는방법

• 텍스트가 자주 바뀌고 찾는 패턴의 길이가 짧은 경우

텍스트를 전처리하는 방법

• 텍스트는 고졍되어 있고 다양한 패턴에 대해 검색하는 경우

표기법

• $\epsilon$ -> 길이가 0인 null 스트링
• $\vert x \vert$ -> 스트링 x의 길이
• $xy$ -> 두 스트링 x와 y의 접속 (x뒤에 y를 붙인 것)

용어

스트링 x, y, w가 주어졌을 때, $x=yw$라면

• 접두부 prefix -> w는 x의 접두부, $w\sqsubset x$
• 접미부 suffix -> y는 x의 접미부, $y\sqsupset x$

---

2. 단순 알고리즘

Naive, Brute-force, Straight-forward

$T=abababcababcaba$, $P=ababcab$

• 

Naive(T[], n, P[], m) {
	입력: T[0...n-1] -> 텍스트, n-> 텍스트 길이
    	 P[0...m-1] -> 패턴,   m-> 패턴 길이
    출력: 패턴이 발생하는 위치
    
    for(i=0; i <= n; i++) {
    	for(j=0; j < m; j++) {
        	if (P[j] != T[i+]) break;
        }
        if (j == m) {
        	printf("텍스트의 i번째 위치에서 패턴 매칭 성공")
        }
    }
}

시간복잡도

최악 $O(m(n-m+1)) = O(mn)$

• 텍스트의 매 위치에서 패턴의 모든 문자를 비교하는 경우

평균 $O(n)$

• 텍스트와 패턴의 모든 글자가 독립적으로 알파벳에서 선택되는 경우

---

3. KMP 알고리즘

단순 알고리즘에서 생긴 의문

불일치가 발생한 앞부분에 대해서,
다시 비교하지 않고 매칭할 수 없을까?

개념

패턴의 전처리를 통해 접미부와 일치하는 최대 진접두부를 구하고,
이를 이용하여 매칭하는 방법

• 불일치가 발생하는 경우 텍스트의 앞부분으로 돌아갈 필요 없이
  불일치가 발생한 텍스트 위치부터 매칭 수행

정의

• $P_k$ -> 패턴의 접두부 $P[0...k]$
• $SP_i$ -> $P_k \sqsupset P_i$인 최대 $P_k$ -> $P_i$의 최대 접두부

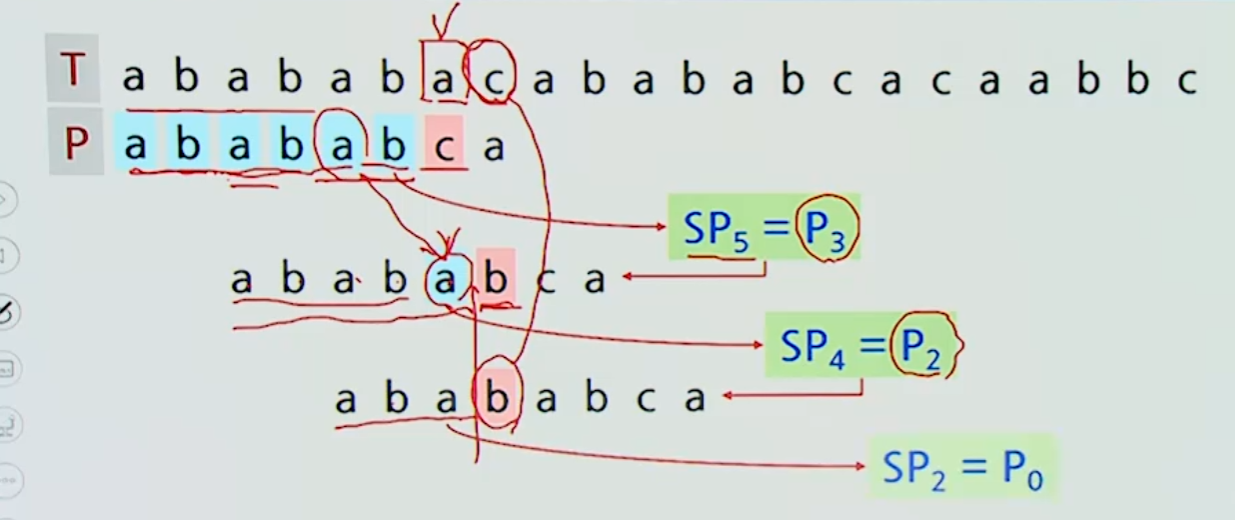
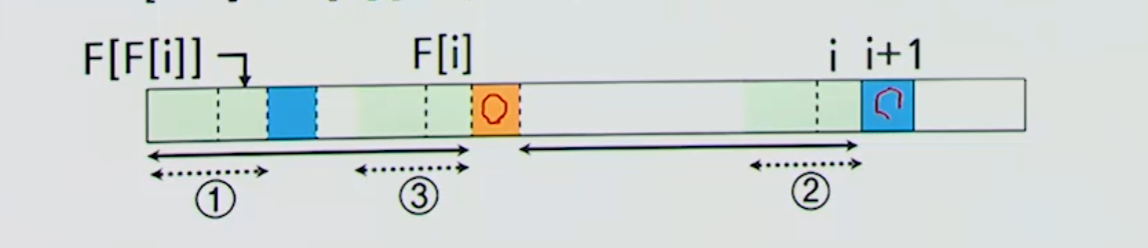
최대 접두부 테이블 $F[0...m-1]$

• $F[i] = max(k: k < i\quad and \quad P_k \sqsupset P_i), \quad 0\leq i\leq m-1$

$F[i]$까지 구했다고 가정하면 $F[i+1] = ?$

• $P[i+1] = P[F[i] + 1]$ => $F[i+1] = F[i] + 1$
  

• $P[i+1] \neq P[F[i] + 1]$ => $F[i+1] < F[i] + 1$
  

PreKMP(P[], m) {
	입력: 패턴 P[0..m-1]
    출력: 최대 접두부 테이블 F[0...m-1]
    
    F[0] = -1;
    k = -1;
    for(i = 1; i <= m-1; i++) { # 최대 접두부 찾기
    	while( k >= 0 && P[k+1] != P[i]) {
        	k = F[k];
        }
        if (P[k+1] == P[i]) { # 마지막 문자 일지
        	k++;
        }
        F[i] = k; # i에서의 최대 접두부 설정
    }
    return F;
}

최대 테이블 구하는 과정

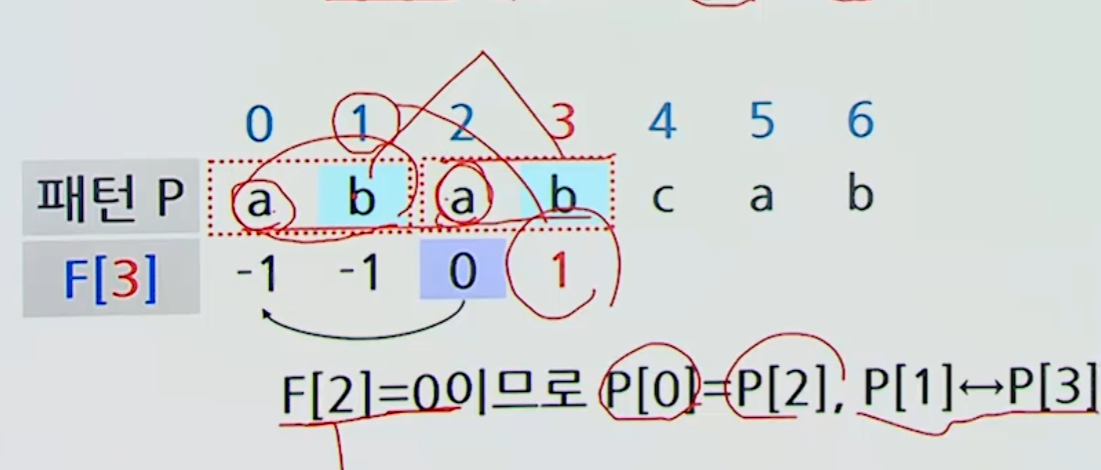
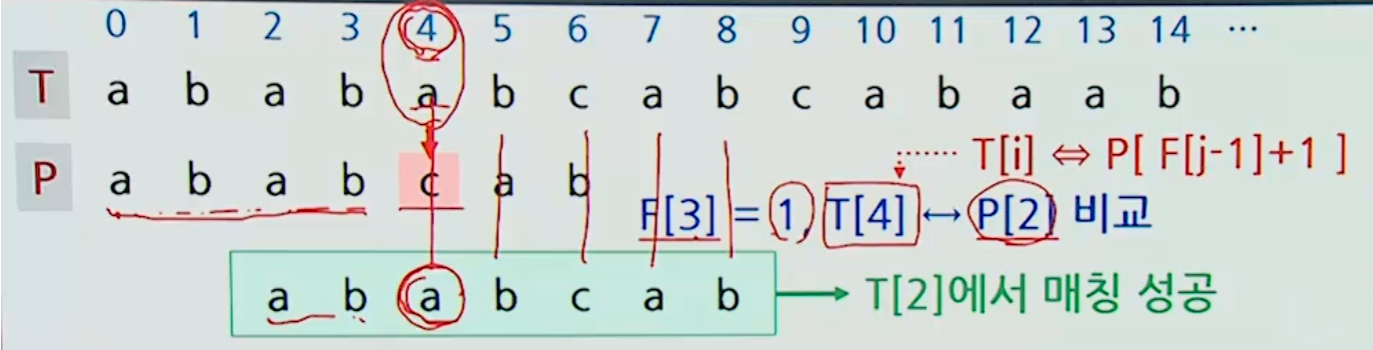
최종 KMP

KMP(T[], n, P[], m) {
	입력: 텍스트 T[0...n-1], 패턴 P[0...m-1]
   	출력: 패턴이 발생하는 위치
    
    F = PreKMP(P, m); # O(m)
    j = -1;
    
    for(i = 0; i <= n-1; i++) { # O(n)
    	while (j >= 0; && P[j+1] != T[i]) j = F[j];
        if (P[j+1] == T[i]) j++;
        if (j == m-1) {
        	T[i-j]에서 매치 존재;
            j = F[j];
        }
    }
}

---

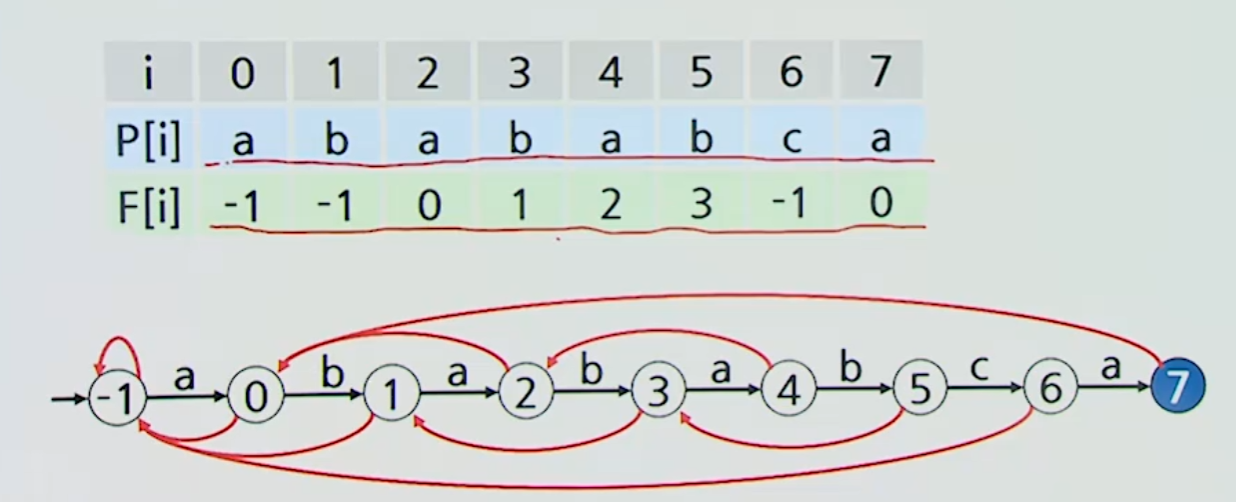
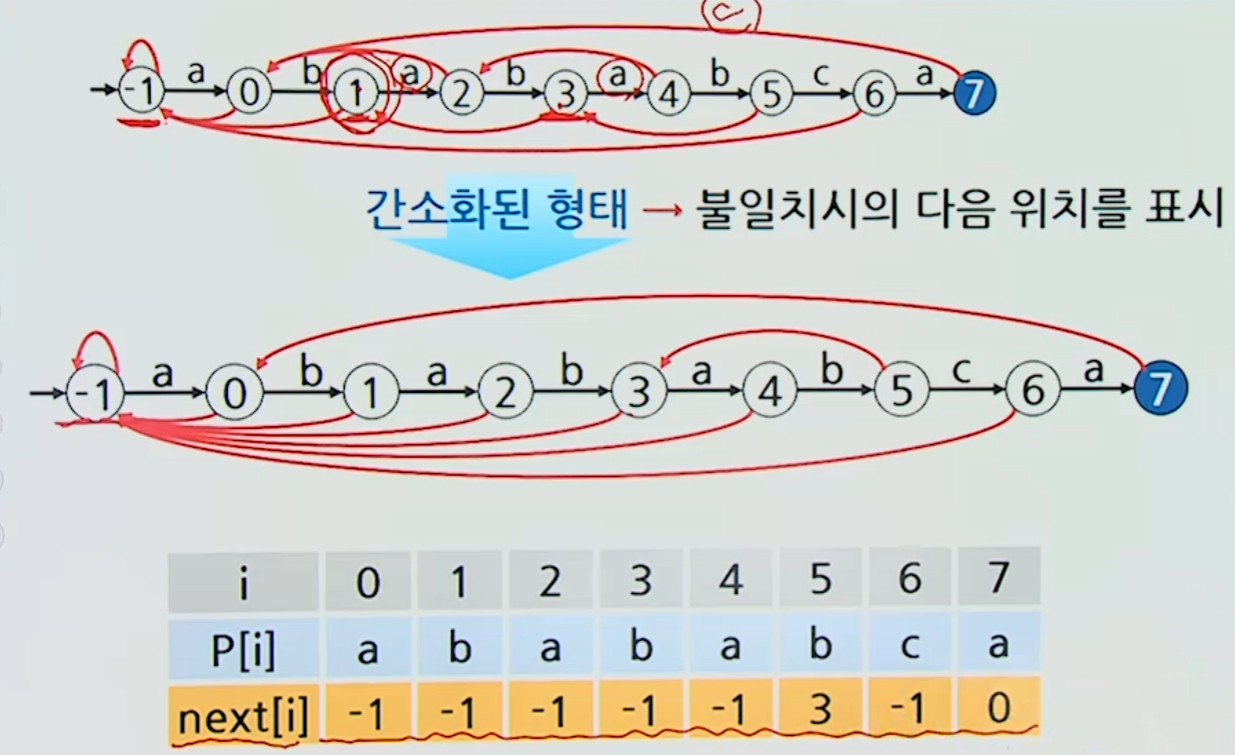
3-1. 유한 상태 기계 (Finite State Machine)

KMP 알고리즘을 발전 시킨 알고리즘

시작 상태로부터 각각의 입력에 따라 상태를 변화시키는 기계

• 붉은 선은 불일치 일때 옮겨갈 경로 (불일치 전이)

---

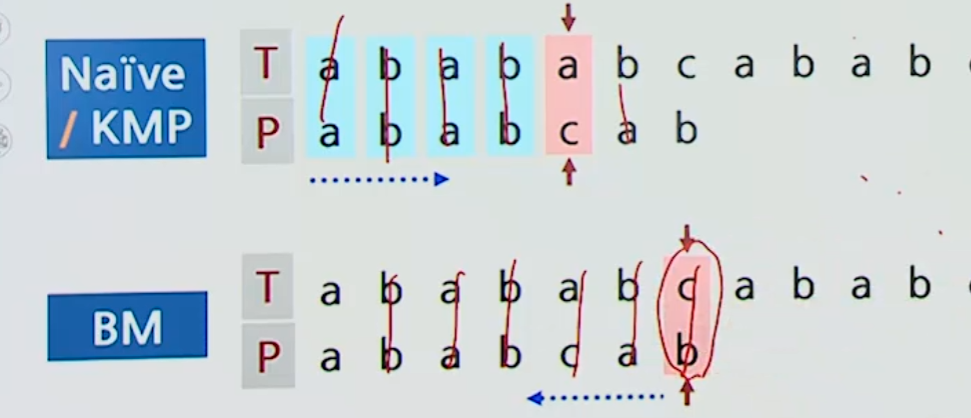
4. 보이어-무어 알고리즘

패턴이 텍스트에 정렬된 각 위치에서 문자의 비교를
우측에서 좌측으로 수행해 나가는 방법

• 불일치 문자 방책 ( bad character heuristics )
• 일치 접미부 방책 ( good suffix heurisitcs )

불일치 문자 방책

알파벳 크기가 비교적 큰 문서에 효과적인 방책

$P[i]$와 $T[j]$의 문자 비교에서 불일치가 발생,
그리고 k가 $T[j]=P[k]$인 최대 k라고 하자.

• $k < i$ 일 때, (k=-1, 즉 패턴에 그 문자가 없는 경우도 포함)

  • $P[k]$가 $T[j]$에 정렬되도록 패턴을 우측으로 $i-k$ 위치만큼 이동한다.

• $k \geq i$ 일 때, 패턴을 우측으로 한 위치 이동 시킨다.

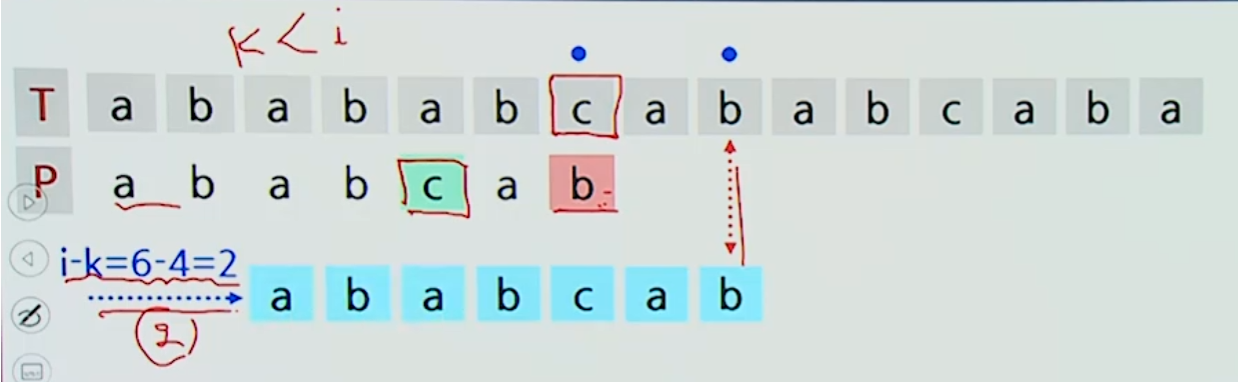
일치 접미부 방책

1) $P[i...,-1] = T[j...j+m]$이었으나 $P[i-1] \neq T[j-1]$

• k < i이고 $P[k...k+m-i-1] = P[i...m-1]$인 최대의 k에 대하여
  $P[k]$가 $T[j]$에 정렬되도록 패턴을 우측으로 $i-k$만큼 이동

2) 1번의 k가 없다면

• P의 접두부가 $P[i...m-1]$의 접미부와 최대로 일치하도록
  우측으로 $m-1-F[m-1]$만큼 이동
  

2) P와 일치가 발생한 경우

• 일치된 T의 접미부와 일치하는 최대 진접두부
  즉, $m-1-F[m-1]$ 만큼 P를 우측으로 이동

BM 알고리즘의 매칭 과정

각 문자의 마지막 위치 계산

• 불일치 문자 방책에서 필요한 각 문자가 나타난 마지막 위치 계산

LastPos(P, m, s, LP) {
	입력: s 알파벳의 집합, 패턴 p, 패턴의 길이 m
    출력: 크기가 양수인 알파벳 집합의 마지막 위치 배열 LP
    
    for (i in s ) LP[i] = -1;
    
    for (i = 0; i < m; i++) LP[P[i]] = i;
}

• 일치 접미부 계산 = 역 패턴에 대한 최대 접미부 계산

GoodSuffix(P, m, skip) {
	입력: 패턴 P[0...m-1]
    출력: 이동거리가 들어있는 배열 skip[-1...m-1]
    
    P^r = reverse(P);
    F = PreKMP(P^r, m);
    
    for (i=-1; i <= m-1; i++) skip[i] = m-1-F[m-1]
    
    for (k = 0; k <= m-1; k++) {
    	i = m-1-F[k];
        if (skip[i] > k-F[k]) skip[i] = k-F[k];
    }
}

• BM 알고리즘

BM(T[], n, P[], m, s) {
	입력: 텍스트 T[0...n-1], 패턴 P[0..m-1], 알파벳 s
    출력: 패턴이 발생한 위치
    
    LastPos(P, m, s, LP); # LP: 알파벳 크기의 마지막 위치 배열
    GoodSuffix(P, m, skip); # skip[]: 일치 접미부 방책의 이동거리
    
    j = 0;
    
    while (j <= n-m) {
    	for (i=m-1; i>=0 && P[i] == T[j+1]; i--); # 문자비교 우 -> 좌
        
        if (i == -1) {
        	printf("패턴이 위치 %d에서 발생", j);
            j = j + skip[-1];
        } else { # 불일치 발생
        
        	# 일치 접미부와 불일치 문자 정책 중 이동거리가 큰 것을 선택
        	j = j + max(skip[i], i-LP[T[j+i]]);  
        }
    }
}

성능

최악 -> $O((n-m+1)m + \vert\sum\vert)$

• 모든 위치에서 패턴 일치가 발생하는 경우
  • LastPos() -> $O(m + \vert \sum \vert)$
  • GoodSuffix() -> $O(m)$
  • BM()의 while문 -> $O((n-m+1)m)$

최선 -> $O(m+n / m + \vert\sum\vert)$

• 실제로 최선이 될 가능성이 높음, 특히 알파벳이 큰 경우