Boosting Index

• Boosting
• Boosting Model
• Bagging VS Boosting
• Ada Boosting
• Gradient Boosting

---

---

Boosting

🔹 Boosting

Boosting은 여러 개의 약한 학습기(Weak Learner)를 순차적으로 학습시키면서, 이전 모델이 틀린 샘플에 가중치를 부여하여 보완하는 앙상블 기법임.

---

🔹 핵심 개념

• 순차적 학습 → 이전 모델이 틀린 샘플을 보완하는 방식
• 가중치 조정 → 틀린 샘플에 더 집중해서 학습
• 모델 결합 → 여러 개의 학습 결과를 합쳐 최종 예측

---

🔹 Boosting 과정

1. 첫 번째 약한 학습기 훈련
2. 틀린 샘플에 가중치 부여
3. 새로운 학습기 훈련 → 기존 모델과 결합
4. 반복해서 성능 개선
5. 최종적으로 모든 학습기의 예측을 조합하여 결과 도출

---

🔹 장점 & 단점

✅ 장점

• 예측 성능이 좋음
• 과적합에 상대적으로 강함
• 다양한 문제(분류/회귀)에 활용 가능

❌ 단점

• 계산량이 많아 느림
• 하이퍼파라미터 튜닝 필요
• 데이터가 적거나 노이즈가 많으면 성능 저하

---

---

🔹 대표적인 Boosting 알고리즘

• AdaBoost
• Gradient Boosting (GBM)
• XGBoost
• LightGBM
• CatBoost

---

Boosting Model

출처: https://corporatefinanceinstitute.com/resources/data-science/boosting/

---

🔹 Boosting 과정

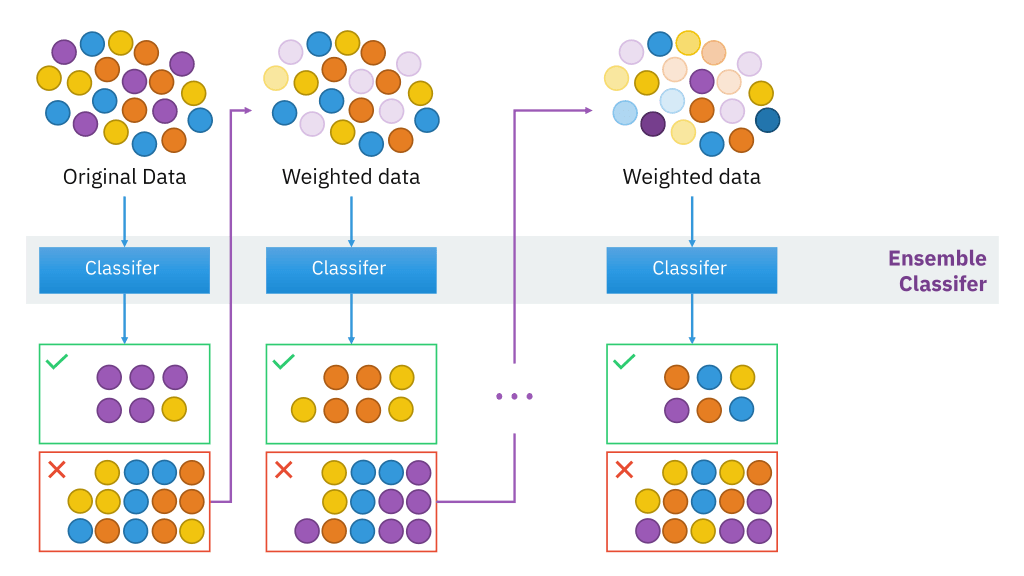
1. Original Data → 처음에는 원본 데이터를 이용해 첫 번째 약한 학습기(Classifier)를 학습
2. Weighted Data → 첫 번째 모델이 틀린 샘플에 더 높은 가중치를 부여
3. 반복 학습 → 다음 학습기가 틀린 샘플을 더 잘 맞추도록 훈련
4. 최종 앙상블(Ensemble Classifier) → 모든 모델의 예측을 조합하여 최종 결과를 생성

즉, Boosting은 각 단계에서 틀린 샘플을 보완하며 학습을 강화하는 방식

---

🔹 Boosting Model

• Boosting Model은 여러 개의 약한 학습기(Weak Learner) 를 조합해 성능이 뛰어난 모델을 만드는 방법
• 약한 학습기들이 서로 보완하면서 점점 더 강력한 예측 모델이 만들어짐.

---

🔹 Boosting Model의 특징

• 약한 학습기를 순차적으로 학습시켜 점점 성능을 개선
• 이전 모델이 틀린 샘플에 가중치를 높여 보완
• 최종적으로 여러 모델의 예측을 결합하여 결과 도출

---

🔹 대표적인 약한 학습기

• 결정 트리(Decision Tree, DT) → 대부분의 Boosting Model은 DT를 기반
• 단, 너무 깊은 트리는 과적합 위험이 있어 보통 얕은 트리(Stump, Depth=1~3) 를 사용

---

🔹 Boosting Model의 기본 구조

1. 첫 번째 약한 학습기를 학습
2. 예측이 틀린 샘플에 가중치를 높여 새로운 학습기 훈련
3. 위 과정을 여러 번 반복
4. 모든 모델의 예측을 합쳐 최종 결과 도출

---

🔹 Boosting Model vs 개별 모델

비교 항목	약한 학습기 (Weak Learner)	Boosting Model
학습 방식	개별적으로 학습	이전 결과를 보완하며 학습
성능	낮음	높음
과적합	쉬움	상대적으로 강함
대표 예시	단일 결정 트리	AdaBoost, XGBoost 등

---

🔹 Boosting Model의 주요 알고리즘

• AdaBoost → 틀린 샘플에 가중치를 부여하는 방식
• Gradient Boosting → 잔차(residual)를 예측하는 방식
• XGBoost, LightGBM, CatBoost → Gradient Boosting을 개선한 모델

---

---

Bagging VS Boosting

출처: https://mathchi.medium.com/what-is-the-boosting-ensemble-method-76610a5cb39f

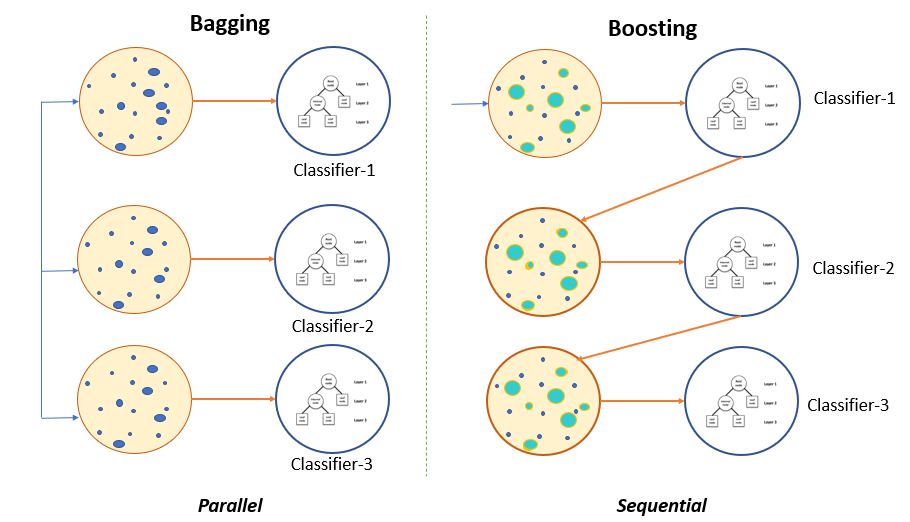
🔹 Bagging vs Boosting

비교 항목	Bagging	Boosting
학습 방식	병렬 학습 (Parallel)	순차 학습 (Sequential)
데이터 샘플링	부트스트랩 샘플링 (랜덤)	이전 모델이 틀린 샘플에 집중
목적	분산(Variance) 감소	편향(Bias) 감소
과적합 방지	비교적 강함	데이터가 적거나 노이즈가 많으면 과적합 위험 있음
대표 알고리즘	Random Forest	AdaBoost, Gradient Boosting, XGBoost, LightGBM, CatBoost

---

---

Ada Boosting(Adaptive Boosting)

출처: https://tkdguq05.github.io/2019/05/15/Boosting/

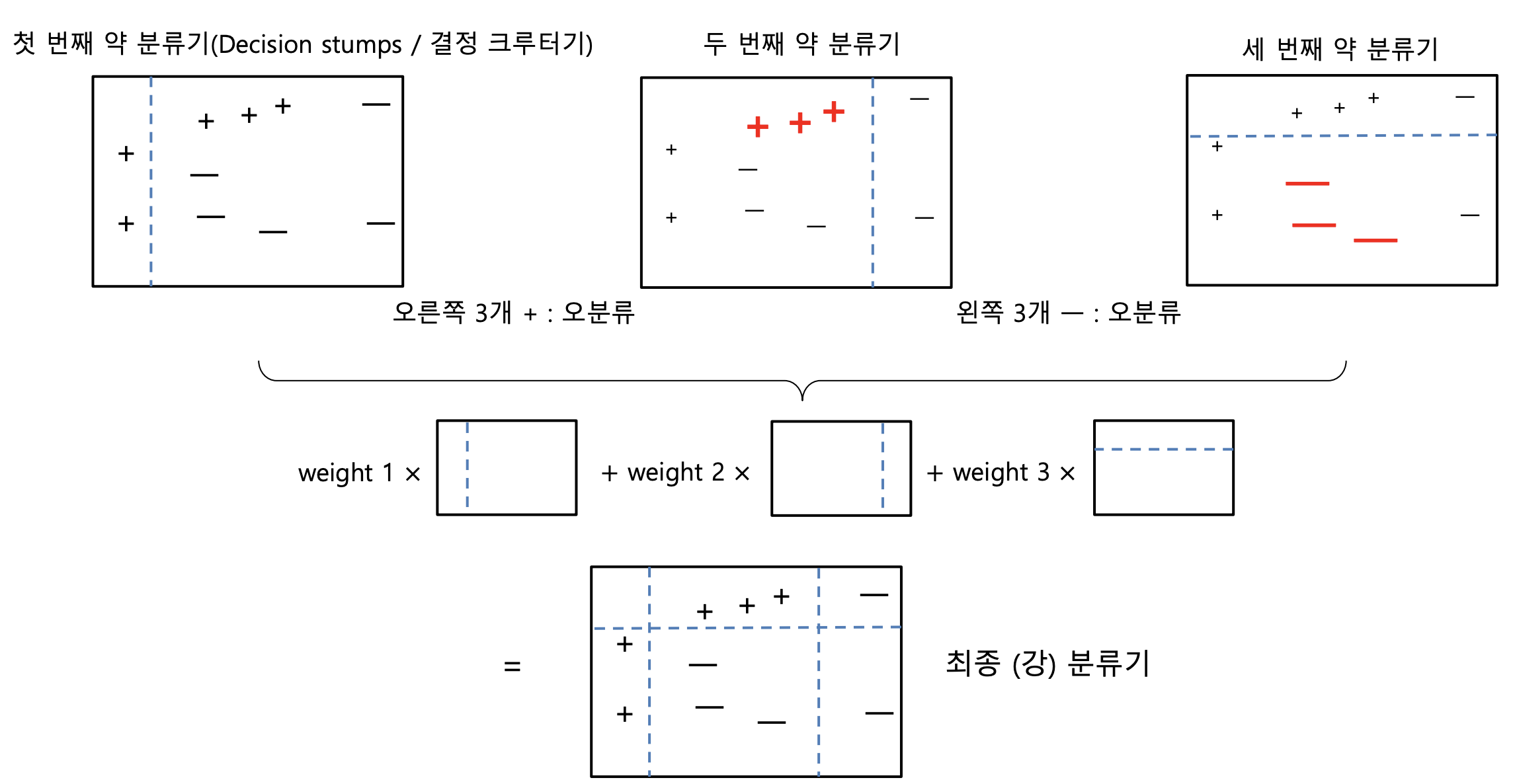
• 첫 번째 약한 분류기 → 간단한 분할, 일부 오분류 발생
• 두 번째 분류기 → 첫 번째 모델이 틀린 샘플을 더 신경 써서 학습
• 세 번째 분류기 → 또 틀린 샘플에 집중하여 학습
• 최종 분류기 → 모든 모델을 가중 평균하여 최적의 결정 경계를 형성

---

🔹 AdaBoost (Adaptive Boosting)

AdaBoost(Adaptive Boosting)는 Boosting의 대표적인 알고리즘.
이전 모델이 틀린 샘플에 가중치를 부여하여 점점 더 정확한 모델을 만드는 방식.

---

🔹 AdaBoost의 핵심 개념

1. 얕은 결정 트리(Decision Stump, Depth=1) 를 약한 학습기로 사용
2. 초기 모델 학습 → 모든 샘플의 가중치는 동일
3. 오분류된 샘플의 가중치 증가 → 다음 모델이 더 집중해서 학습
4. 새로운 모델을 학습하고, 가중 평균하여 최종 예측 도출

즉, 틀린 샘플에 집중하면서 점진적으로 모델 성능을 향상시키는 구조임.

---

🔹 AdaBoost 과정

1️⃣ 첫 번째 약한 학습기(Weak Learner) 학습

• 모든 샘플에 동일한 가중치 부여 후 학습
• 틀린 샘플을 확인

2️⃣ 가중치 업데이트

• 오분류된 샘플의 가중치를 증가
• 잘 맞춘 샘플의 가중치는 감소

3️⃣ 새로운 학습기 학습

• 업데이트된 가중치를 반영하여 다시 학습
• 다시 오분류된 샘플의 가중치를 조정

4️⃣ 반복 학습

• 여러 개의 약한 학습기를 쌓아가면서 점점 성능을 개선

5️⃣ 최종 예측

• 모든 학습기의 예측 결과를 가중 평균(weighted sum) 하여 최종 결정

---

🔹 AdaBoost의 특징

✅ 장점

• 과적합이 비교적 적고 성능이 뛰어남
• 간단한 모델(얕은 트리)도 강력한 성능을 발휘 가능
• 다양한 분류/회귀 문제에 적용 가능

❌ 단점

• 이상치(Outlier)에 민감함 → 일부 샘플에 너무 높은 가중치가 부여될 수 있음
• 연산량이 많아질수록 속도가 느려질 수 있음

결론: AdaBoost: 약한 모델을 여러 개 조합하여 점진적으로 개선하는 방식의 Boosting 알고리즘

---

---

Gradient Boosting

출처: https://corporatefinanceinstitute.com/resources/data-science/boosting/

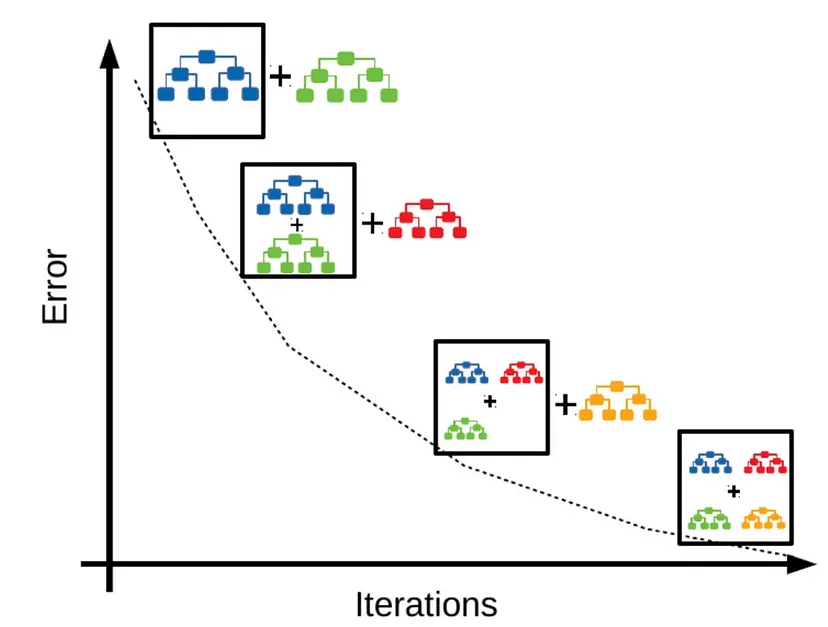
X축 (Iterations) → 반복 횟수
Y축 (Error) → 오류(손실) 감소

• 첫 번째 약한 학습기(파란색 트리)로 시작 → 오류가 남음
• 두 번째 학습기(초록색 트리) → 첫 번째 모델이 못 맞춘 부분을 보완
• 세 번째 학습기(빨간색 트리) → 여전히 남은 오류를 추가로 보완
• 네 번째 학습기(노란색 트리) → 오류가 점점 줄어 최종적으로 강한 모델 형성

---

Gradient Boosting 알고리즘 수식 분석

• Gradient Boosting은 잔차(Residual)를 줄이는 방향으로 학습하는 알고리즘
  -> 기존 모델이 못 맞춘 부분을 새로운 모델이 학습하면서 점진적으로 개선

---

0. Input: 초기 데이터 및 모델 설정

입력 데이터

데이터셋:

• $X = \{x_1, x_2, ..., x_n\}$ (특징값, Feature)
• $Y = \{y_1, y_2, ..., y_n\}$ (정답값, Target)
• 손실 함수 $L(y, F(x))$ (예: MSE, Log Loss 등)

목표:
모델 $F(x)$ 를 학습하여 예측값 $\hat{y} = F(x)$ 가 정답 $y$ 와 최대한 가깝도록 학습

---

1. 초기 모델 $F_0(x)$ 설정**

가장 간단한 기본 모델을 설정

• 회귀 문제(Regression): 평균값 사용

  $F_0(x) = \arg\min_{\gamma} \sum_{i=1}^{n} L(y_i, \gamma)$

  → 예: 평균 $\bar{y}$ 를 사용 → $F_0(x) = \bar{y}$

• 분류 문제(Classification): 로그 확률 사용

  $F_0(x) = \log \frac{p}{1-p}$

  → $p$ 는 목표 클래스의 확률

---

2. 반복 학습 (m = 1 to M)

(1) 잔차(Residual) 계산

현재 모델 $F_{m-1}(x)$ 로 예측한 값과 실제 값 $y$ 차이(잔차)를 계산

• 손실 함수 $L(y, F(x))$ 의 기울기(Gradient) 를 이용해 잔차 계산
• 회귀 문제: $r_{im} = y_i - F_{m-1}(x_i)$ (MSE 기준)
• 분류 문제: 로그 확률 기반으로 계산

$r_{im}$ 는 현재 모델이 잘못 예측한 부분 → 다음 모델이 학습해야 하는 부분

---

(2) 새로운 모델(결정 트리) 학습

잔차 $r_{im}$ 를 새로운 목표값(Target)으로 설정하여 새로운 트리 학습

• 새로운 학습 데이터:
  $(X, r_{im})$

  $X$ 를 입력값으로 하고, $r_{im}$ 를 정답값(Target)으로 설정하여 결정 트리 학습

---

(3) 새로운 모델의 최적 가중치 계산

• 새로운 트리가 학습한 잔차를 얼마나 반영할지(가중치 $\gamma )$ 를 결정
• 보통 선형 탐색(Line Search) 방법을 사용

---

(4) 모델 업데이트

새로운 모델을 기존 모델에 추가하여 업데이트

• $\nu$ (Learning Rate): 학습 속도 조절
• $\sum_{j=1}^{J_m} \gamma_{jm} 1(x \in R_{jm})$: 새롭게 추가된 트리의 예측값

현재 모델 $F_{m-1}(x)$ 에 새로운 트리를 더하면서 예측을 점진적으로 개선

---

3. Output: 최종 모델 (F_M(x))

• 초기 모델 + 여러 개의 트리 모델의 조합
• 각 트리는 이전 모델이 틀린 부분을 학습하여 점진적으로 개선

---

추가 설명

Gradient Boosting에서 $\gamma_m h_m(x)$라는 표현은
새로운 트리의 예측값과 그 가중치를 곱한 형태를 의미
새로운 트리를 기존 모델에 추가하는 방식

---

1. Gradient Boosting의 일반적인 업데이트 공식

여기서:

• $F_m(x)$ : 현재까지 학습된 모델 (이전 모델 + 새로운 트리)
• $F_{m-1}(x)$ : 이전까지의 모델
• $\nu$ : 학습률 (Learning Rate)
• $h_m(x)$ : 새롭게 학습한 트리
• $\gamma_m$ : 새로운 트리에 곱할 최적 가중치 (Weight)

즉, 새로운 트리 $h_m(x)$을 학습한 후, 최적의 가중치 $\gamma_m$을 곱해서 기존 모델에 추가하는 방식

---

2. $h_m(x)$의 의미 (새로운 트리)

• $h_m(x)$는 현재 모델이 틀린 부분(잔차)을 예측하는 새로운 결정 트리
• 즉, 이전 모델의 예측값과 실제 값 $y$의 차이를 학습
• Gradient Boosting에서는 손실 함수 $L(y, F(x))$의 기울기(Gradient)를 기반으로 $h_m(x)$을 학습

---

3. $\gamma_m$의 의미 (최적 가중치)

• 새로운 트리 $h_m(x)$를 학습한 후, 그 값을 얼마나 반영할지 결정하는 최적의 가중치를 찾음
• 이때 $\gamma_m$은 손실 함수 $L(y, F(x))$가 최소가 되도록 최적화

• 즉, 새로운 트리의 가중치를 조정하여 손실 함수가 최소화되도록 최적화하는 과정
• 회귀 문제에서는 보통 선형 탐색(Line Search)을 사용하여 $\gamma_m$를 찾음.

---

4. 전체적인 업데이트 과정

1. 초기 모델 설정: $F_0(x) = \bar{y}$ (회귀의 경우 평균값)
2. 잔차 계산: $r_{im} = - \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}$
3. 새로운 트리 $h_m(x)$학습: $h_m(x)$은 $r_{im}$을 예측하도록 학습됨
4. 최적 가중치 $\gamma_m$ 찾기: $\gamma_m = \arg\min_{\gamma} \sum L(y_i, F_{m-1}(x_i) + \gamma h_m(x_i))$
5. 모델 업데이트: $F_m(x) = F_{m-1}(x) + \nu \gamma_m h_m(x)$

---

5. Gradient Boosting 업데이트의 핵심

✔ $h_m(x)$: 새로운 트리, 기존 모델이 틀린 부분(잔차)을 학습
✔ $\gamma_m$: 새로운 트리의 가중치, 최적의 값을 찾아 손실을 최소화
✔ $F_m(x)$: 이전 모델에 $\gamma_m h_m(x)$을 추가하여 점진적으로 개선
✔ 트리의 미분은 직접 구하지 않고, 손실 함수의 미분을 기반으로 업데이트

즉, Gradient Boosting은 새로운 트리를 학습한 후, 최적의 가중치를 곱해 기존 모델에 추가하는 방식

---

Gradient Boosting 핵심 요약

✅ 잔차(Residuals)를 학습하여 점진적으로 성능 개선
✅ 손실 함수(Gradient) 기반으로 모델 업데이트
✅ 기존 예측 + 새로운 예측의 가중합 방식으로 최종 모델 형성
✅ AdaBoost와 차이점: AdaBoost는 오분류된 샘플에 가중치를 부여하는 방식, Gradient Boosting은 잔차를 줄이는 방향으로 학습

---

---