Decision Tree (의사 결정 트리)

Decision Tree

의사 결정 트리

의사 결정 트리(Decision Tree)는 데이터를 계층적으로 분할하여 예측을 수행하는 트리 기반 머신러닝 알고리즘

주어진 데이터를 여러 개의 분할 기준(규칙)을 사용하여 나누고, 트리 구조를 통해 최종 예측을 수행

✅ 특징

• 해석이 쉬운 모델 → 사람이 이해하기 직관적
• 비선형 관계도 학습 가능
• 과적합 가능성 있음 → 가지치기(Pruning) 필요
• 명확한 분류 경계를 제공

---

Loss Function (손실 함수)

결정 트리는 데이터를 나누면서 손실 함수(Loss Function)를 최소화하는 방향으로 학습된다.

손실 함수는 모델의 예측값이 실제값과 얼마나 차이가 있는지를 나타내는 지표이다.

결정 트리에서는 주로 회귀 트리(Regression Tree)에서 손실 함수를 사용한다.

Square Loss (제곱 손실)

• $y_d$: 실제값 (Target)
• $\hat{y}_d$: 예측값 (Output)

Mean Square Loss (평균 제곱 오차, MSE)

• MSE는 오류를 평균 내어 사용하는 방식으로 회귀 트리에서 분할 기준으로 사용된다.

📌 손실 함수가 낮을수록 모델이 더 좋은 성능을 보임!

---

Information (정보)

정보(Information)는 노드의 불확실성(Uncertainty)을 측정하는 지표

결정 트리는 정보 이득(Information Gain)이 높은 기준을 사용하여 데이터를 분할

확률 개념과 정보량

사건이 발생할 확률이 낮을수록 더 많은 정보량을 갖는다.

예를 들어:

• 동전 던지기(50%) → $P(X) = 0.5$ → 정보량이 적음
• 로또 당첨 확률(0.000001%) → $P(X) = 0.000001$ → 정보량이 큼

---

Entropy (엔트로피)

엔트로피(Entropy)는 노드의 혼합 정도(불순도, Impurity)를 측정하는 척도이다.
값이 0이면 완전히 순수한 노드, 1에 가까울수록 불순한 노드를 의미한다.

✅ 설명

• $p_i$ = 특정 클래스 $i$에 속할 확률
• 값이 0에 가까울수록 순수한 노드, 1에 가까울수록 혼합된 노드

📌 엔트로피는 불순도를 계산하는 또 다른 방법으로, 정보 이득(Information Gain) 계산에 사용됨.

---

Impurity (불순도)

정의

불순도(Impurity)는 노드 내 데이터가 얼마나 섞여 있는지를 나타내는 지표이다.
결정 트리는 불순도를 최소화하는 방향으로 학습된다.

✅ 불순도가 낮을수록 노드의 순도가 높아짐
❌ 불순도가 높으면 노드가 혼합된 상태

---

불순도 공식 (식)

불순도를 측정하는 대표적인 방법은 Gini Index(지니 지수)와 Entropy(엔트로피)이다.

1. 지니 지수(Gini Index)

   $Gini = 1 - \sum_{i=1}^{C} p_i^2$

2. 엔트로피(Entropy)

   $H(S) = - \sum_{i=1}^{C} p_i \log_2 p_i$

---

Gini Index (지니 지수)

지니 지수(Gini Index)는 불순도를 측정하는 대표적인 방법이다.

✅ 설명

• $p_i$ = 특정 클래스 $i$에 속할 확률
• 값이 0에 가까울수록 순수한 노드, 1에 가까울수록 혼합된 노드

📌 지니 지수는 계산이 간단하여 CART(Classification and Regression Tree) 알고리즘에서 자주 사용됨

---

Information Gain (정보 이득)

✅ 설명

• $H(parent)$: 부모 노드의 엔트로피
• $P(i)$: 자식 노드 ( i )의 확률
• $H(i)$: 자식 노드의 엔트로피

📌 정보 이득이 클수록 좋은 분할 기준!

Information Gain Ratio (정보 이득 비율)

정보 이득이 높은 특성이 많을 경우 편향된 분할이 발생할 수 있다.
이를 보완하기 위해 정보 이득 비율(Information Gain Ratio, IG Ratio)을 사용한다.

✅ 설명

• $H(attribute)$ = 속성의 엔트로피

📌 정보 이득 비율을 사용하면 불균형 문제를 해결

---

결정 트리의 종류

분류 트리 (Classification Tree)

• 목표: 클래스를 예측
• 불순도 측정: 지니 지수(Gini Index) 또는 엔트로피(Entropy) 사용

회귀 트리 (Regression Tree)

• 목표: 연속적인 값(숫자)을 예측
• 불순도 측정: MSE(Mean Squared Error) 사용

---

결정 트리의 모델 학습

분할 (Splitting)

• 정보 이득(Information Gain)이 최대가 되는 지점 선택

가지치기 (Pruning)

• 사전 가지치기(Pre-Pruning): 트리 깊이 제한
• 사후 가지치기(Post-Pruning): 트리 생성 후 불필요한 노드 제거

예측 (Prediction)

• 트리의 루트에서 분기 노드를 따라 이동하여 예측 수행

---

python 예시

iris 데이터, 라이브러리 불러오기

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

iris = load_iris()
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2,random_state=42)

---

Decision Tree 학습하기

DT = DecisionTreeClassifier()
DT.fit(x_train, y_train)
print('accuracy:{:.2f}'.format(DT.score(x_test,y_test)))
from sklearn import tree
tree.plot_tree(DT)
plt.show()

out:

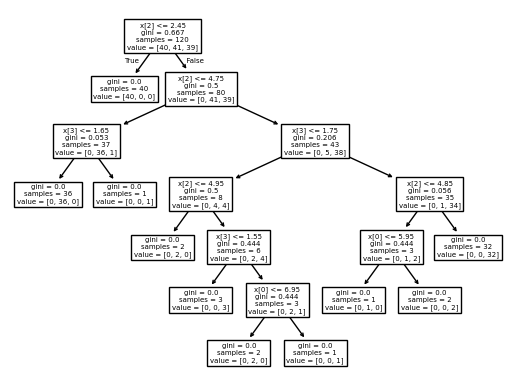
• from sklearn.tree import DecisionTreeClassifier 로 불러오고
• DecisionTreeClassifier로 학습

---

시각화

!pip install graphviz

• path까지 조정 해야함

from sklearn.tree import export_graphviz
from graphviz import Source
export_graphviz(DT,
                out_file = 'iris_tree.dot',
                feature_names=iris.feature_names,
                class_names=iris.target_names,
                rounded=True,
                filled =True)

graph = Source.from_file('iris_tree.dot')
graph.view()                

out :

---

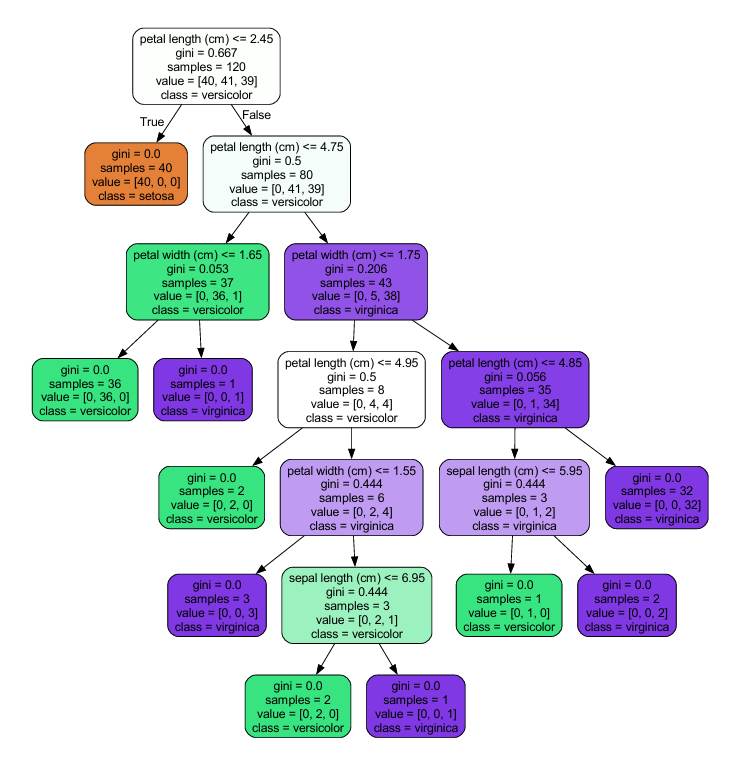
Feature Importance

import seaborn as sns
import numpy as np
print('Feature importance : \n:{0}'.format(np.round(DT.feature_importances_,3)))
for name, value in zip(iris.feature_names, DT.feature_importances_):
    print('{0} : {1:.3f}'.format(name,value))
sns.barplot(x=DT.feature_importances_, y=iris.feature_names)
plt.show()

out :

Feature importance : 
:[0.033 0.    0.889 0.077]
sepal length (cm) : 0.033
sepal width (cm) : 0.000
petal length (cm) : 0.889
petal width (cm) : 0.077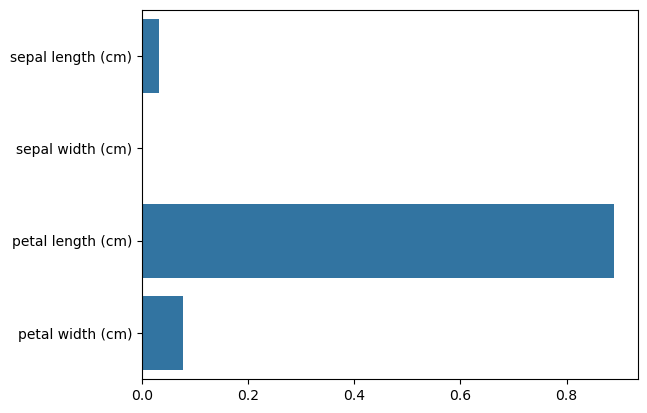

해석

결정 트리(Decision Tree) 모델의 Feature Importance(특성 중요도)

코드 해석:
1. DT.feature_importances_

• 결정 트리 모델이 학습한 후 각 특성이 예측에 얼마나 중요한지
• 값이 클수록 해당 특성이 모델의 판단에 더 중요한 역할

2. 출력 부분 (print)

   • np.round(DT.feature_importances_,3) → 소수점 셋째 자리까지 반올림해서 출력.
   • for name, value in zip(iris.feature_names, DT.feature_importances_)
     → iris.feature_names (특성 이름)과 중요도를 같이 출력.

3. Seaborn의 barplot

   • sns.barplot(x=DT.feature_importances_, y=iris.feature_names)
   • 특성 중요도를 막대그래프로 시각화.
   • 가로 막대그래프가 그려지고, 길이가 길수록 중요한 특성.

그래프 해석:

• petal length (cm) 가 가장 중요한 특성 (가장 긴 막대).
• sepal width (cm) 는 거의 중요하지 않음 (거의 0에 가까운 값).
• DecisionTreeClassifier를 사용하면 모델이 어떤 특성에 집중하는지 알 수 있음.