회귀분석1

회귀분석(Regression Analysis)

📌 1. 회귀분석이란?

회귀분석(Regression Analysis)은 독립 변수(X)와 종속 변수(Y) 간의 관계를 수학적으로 모델링하여 예측하는 기법
특히, 선형 회귀(Linear Regression)는 데이터를 가장 잘 설명하는 직선을 찾는 것

단순 선형 회귀(Simple Linear Regression)

단순 선형 회귀는 하나의 독립 변수$X$와 하나의 종속 변수$Y$ 간의 관계를 직선으로 모델링

여기서,

• $Y$ : 예측값 (Target)
• $X$ : 입력값 (Feature)
• $\beta_0$ : 절편(Intercept)
• $\beta_1$ : 기울기(Slope)
• $\epsilon$ : 오차(Term Error, White Noise)

📌 목적:

• 데이터의 패턴을 찾아 가장 적절한 직선(Regression Line) 을 만드는 것.
• 예측값과 실제값의 차이(오차)가 최소가 되도록 최적화하는 것.

---

📌 2. 단순 선형 회귀 모델 추정 방법

"여러 개의 직선 중에서 가장 좋은 직선을 찾으려면?"
직선과 데이터의 차이가 평균적으로 가장 작아지는 직선을 찾는 것.

💡 최적의 회귀선을 찾는 방법
1. 오차(Error)를 계산하고 최소화하는 것이 핵심!
2. 평균 제곱 오차(MSE)를 이용해 가장 좋은 직선을 찾음.

---

📌 3. 오차(Error) 계산

모델이 얼마나 정확한지 측정하려면 실제값과 예측값의 차이(잔차, Residuals) 를 계산.

📌 잔차의 제곱합(SSE, Sum of Squared Errors)

이렇게 오차를 제곱하는 이유
✅ 오차가 양수/음수에 관계없이 절댓값으로 반영
✅ 미분이 가능한 형태

---

📌 4. 비용 함수(Cost Function)

오차를 최소화하는 것이 목표이므로, 비용 함수(Cost Function)를 최소화
평균 제곱 오차(MSE, Mean Squared Error)

• 값이 작을수록 더 좋은 모델.
• 결국 이 값을 최소화하는 최적의 기울기$(beta_1)$와 절편$(\beta_0)$ 찾기

---

5. 비용 함수 미분 (Gradient Calculation)

경사하강법(Gradient Descent)을 사용하여 비용 함수를 최소화하는 방향으로 이동하려면, 편미분 사용

📌 비용 함수 $J(\beta_0, \beta_1)$를 $\beta_0$, $\beta_1$에 대해 각각 편미분

(1) 기울기 $\beta_1$ 에 대한 편미분

체인 룰을 사용하여 미분:

즉,

---

(2) 절편 $\beta_0$ 에 대한 편미분

벡터 연산으로 표현,

---

📌 6. 경사 하강법 (Gradient Descent)

경사하강법은 오차를 최소화하는 최적의 $(\beta_0, \beta_1)$ 을 찾기 위한 최적화 알고리즘

핵심 아이디어

• 비용 함수 $(J(\beta_0, \beta_1))$ 의 기울기(Gradient) 를 계산하여,
• 기울기가 낮아지는 방향으로 $(\beta_0, \beta_1)$ 을 업데이트하는 방식.

📌 업데이트 공식

여기서,

• $\alpha$ (learning rate, 학습률): 한 번에 이동하는 크기
• $\frac{\partial J}{\partial \beta_1}$: 비용 함수의 미분 값(Gradient)
• 즉, 기울기의 반대 방향으로 이동하면서 오차를 줄이는 방식 🚀

📌 경사하강법 작동 원리
1️⃣ 먼저 가중치를 랜덤하게 초기화
2️⃣ 비용 함수 $J(\beta)$ 의 기울기(Gradient)를 계산
3️⃣ 기울기 방향의 반대쪽으로 $\beta_1, \beta_0$ 업데이트
4️⃣ 2~3 과정을 반복하여 최적의 $\beta_1, \beta_0$ 찾기

---

📌 7. 최적의 학습률(Learning Rate) 설정

학습률$\alpha$이 너무 크거나 작으면 문제 발생.

✅ 적절한 학습률 선택이 중요!

• 너무 크면 → 발산 (최적값을 지나쳐버림)
• 너무 작으면 → 학습이 느림 (최적값을 찾는 데 오랜 시간이 걸림)

보통 $0.01 \sim 0.1$ 사이의 값을 많이 사용.

---

🎯 정리

✅ 회귀분석: 독립 변수(X)와 종속 변수(Y) 간의 관계를 찾는 모델
✅ 단순 선형 회귀: 하나의 X로 Y를 예측하는 가장 기본적인 회귀
✅ 오차 계산 (SSE, MSE): 예측값과 실제값의 차이를 최소화하는 방식
✅ 경사하강법: 오차를 줄이며 최적의 $\beta_1, \beta_0$ 찾기
✅ 학습률$\alpha$ 설정: 너무 크거나 작으면 학습이 제대로 안됨

---

아래와 같이 함수별 설명과 코드를 정리하면 velog에 게시하기 좋을 거야! 🚀

---

8. 📌 Python으로 구현하는 선형 회귀(Linear Regression)

경사하강법(Gradient Descent)과 확률적 경사하강법(Stochastic Gradient Descent, SGD) 을 이용하여 단순 선형 회귀를 직접 구현

---

📌 1. 데이터 생성

먼저, $y = 4x + 6$ 의 선형 관계를 가지는 데이터를 생성하자.
여기에 약간의 노이즈를 추가하여 현실적인 데이터처럼 만들었다.

import numpy as np
import matplotlib.pyplot as plt

# y = 4x+6 (w1 = 4, w0 = 6), noise 추가
X = 2 * np.random.rand(100,1)
y = 6 + 4 * X + np.random.rand(100,1)  # 약간의 노이즈 추가

---

📌 2. 비용 함수 (Cost Function)

Mean Squared Error (MSE, 평균 제곱 오차) 를 비용 함수로 사용한다.
MSE는 모델의 예측값과 실제값의 차이를 제곱하여 평균낸 값이다.

def get_cost(y, y_pred):
    N = len(y)
    cost = np.sum(np.square(y - y_pred)) / N
    return cost

---

📌 3. 가중치 업데이트 함수 (get_weight_updates)

경사하강법을 이용해 가중치 $w_0$, $w_1$을 업데이트하는 함수
각 가중치는 비용 함수의 편미분 값을 이용하여 업데이트된다.

📌 역할

• 입력 데이터를 이용하여 현재 가중치(w1, w0)를 업데이트한다.
• 경사하강법(Gradient Descent)의 핵심 수식을 적용한다.

def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
    N = len(y)  
    w1_update = np.zeros_like(w1)
    w0_update = np.zeros_like(w0)
    
    y_pred = np.dot(X, w1.T) + w0  # 예측값
    diff = y - y_pred  # 오차 계산
    
    w0_factors = np.ones((N,1))  
    w1_update = (-2/N) * learning_rate * (np.dot(X.T, diff))
    w0_update = (-2/N) * learning_rate * (np.dot(w0_factors.T, diff))
    
    return w1_update, w0_update

---

📌 4. 배치 경사하강법 (Gradient Descent)

배치 경사하강법(Batch Gradient Descent)은 전체 데이터를 사용하여 가중치를 업데이트하는 방식이다.
모든 데이터를 활용하므로 수렴 속도가 안정적이지만 계산량이 많을 수 있다.

📌 역할

• get_weight_updates()를 반복 실행하여 최적의 가중치(w1, w0)를 찾는다.
• 모든 데이터를 사용하여 한 번에 업데이트하는 방식이다.

def gradient_descent_steps(X, y, iters=10000):
    w0 = np.zeros((1,1))
    w1 = np.zeros((1,1))
    
    for ind in range(iters): 
        w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
        w1 = w1 - w1_update  
        w0 = w0 - w0_update  
    
    return w1, w0

💡 실행 결과

w1, w0 = gradient_descent_steps(X, y, iters=1000)
print('w1:{0:.3f} w0:{1:0.3f}'.format(w1[0,0], w0[0,0]))
y_pred = w1[0,0] * X + w0
print('Gradient Descent Total Cost: {:.4f}'.format(get_cost(y, y_pred)))

plt.scatter(X, y)
plt.plot(X, y_pred)
plt.show()

out:

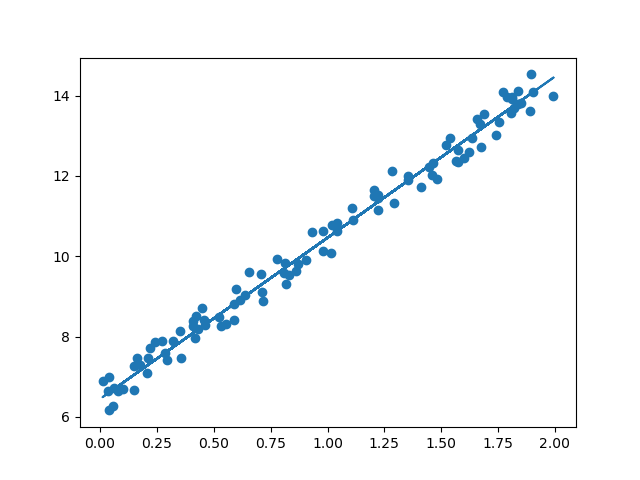
w1:4.013 w0:6.450
Gradient Descent Total Cost: 0.0837

---

📌 5. 확률적 경사하강법 (Stochastic Gradient Descent, SGD)

확률적 경사하강법(SGD)은 일부 샘플(미니배치)를 사용하여 가중치를 업데이트하는 방식이다.
배치 경사하강법보다 계산량이 적고 빠르게 수렴하지만, 최적해에 도달하기까지 변동성이 클 수 있다.

📌 역할

• 매 반복마다 무작위로 일부 데이터(batch)를 선택하여 업데이트한다.
• 데이터가 많을 경우 연산량이 줄어들어 더 빠르게 학습할 수 있다.

def stochastic_gradient_descent_steps(X, y, batch_size=10, iters=10000):
    w0 = np.zeros((1,1))
    w1 = np.zeros((1,1))
    
    for ind in range(iters): 
        stochastic_random_index = np.random.permutation(X.shape[0])
        sample_X = X[stochastic_random_index[:batch_size]]
        sample_y = y[stochastic_random_index[:batch_size]]

        w1_update, w0_update = get_weight_updates(w1, w0, sample_X, sample_y, learning_rate=0.01)  
        w1 = w1 - w1_update  
        w0 = w0 - w0_update  
    
    return w1, w0

💡 실행 결과

w1, w0 = stochastic_gradient_descent_steps(X, y, iters=1000)
print('w1:' , round(w1[0,0],3), 'w0:', round(w0[0,0],3))
y_pred = w1[0,0] * X + w0
print('Stochastic Gradient Descent Total Cost: {0:.4f}'.format(get_cost(y, y_pred)))

plt.scatter(X, y)
plt.plot(X, y_pred)
plt.show()

out:

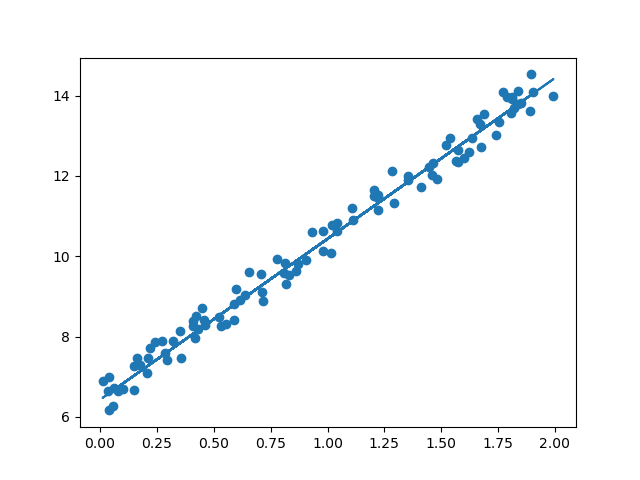
w1: 4.003 w0: 6.432
Stochastic Gradient Descent Total Cost: 0.0846

---

📌 6. 배치 경사하강법 vs 확률적 경사하강법 비교

방법	특징	장점	단점
배치 경사하강법	전체 데이터를 사용하여 한 번에 업데이트	수렴 속도가 안정적	데이터가 많으면 연산량이 많아짐
확률적 경사하강법	일부 데이터를 무작위로 선택하여 업데이트	빠른 학습 가능, 데이터가 많을 때 유리	변동성이 크고 최적해 주변에서 불안정할 수 있음

---

📌 마무리

이번 글에서는 경사하강법(Gradient Descent)과 확률적 경사하강법(SGD)를 이용한 선형 회귀 모델을 직접 구현해 보았다.
데이터를 생성하고, 비용 함수를 최소화하는 과정을 함수별로 정리했다.

✅ 배치 경사하강법은 전체 데이터를 사용하여 학습하며, 안정적이지만 연산량이 많다.
✅ 확률적 경사하강법은 일부 데이터만 사용하여 학습하며, 빠르지만 변동성이 크다.
✅ 두 방법 모두 장단점이 있으므로 **상황에 맞게 선택하여 사용

---