⭐Greedy Algorithm(탐욕적인 알고리즘)이란?
결정을 해야할 때마다 그 순간 가장 좋다고 생각하는 것을 해답으로 선택함으로써 최종적인 해답에 도달하는 알고리즘
즉, 미래를 생각하지 않고 각 단계에서 가장 최선의 선택을 하는 기법이다.
⭐Greedy Algorithm의 설계 절차
- Selection procedure (선정과정)
- 현재 상태에서 가장 좋으리라고 생각되는(greedy criterion)
해답을 선택한다.
- Feasibility check (적절성 점검)
- 새로 얻은 해답을 해답모음(solution set)에 포함하시키는 것이 적 절한지 점검한다.
- Solution check (해답 점검)
- 새로 얻은 해답모음이 해인지를 점검한다.
⭐Greedy Algorithm VS DP
둘 다 최적화 문제를 푸는데 적합하지만
Greedy Approach는 알고리즘이 최적인지 증명해야한다.
또한 DP는 때로는 불필요하게 복잡하지만 Greedy Approach는 알고리즘이 존재할 경우 보통 더 효율적이다.
⭐Prim's Algorithm(MST)
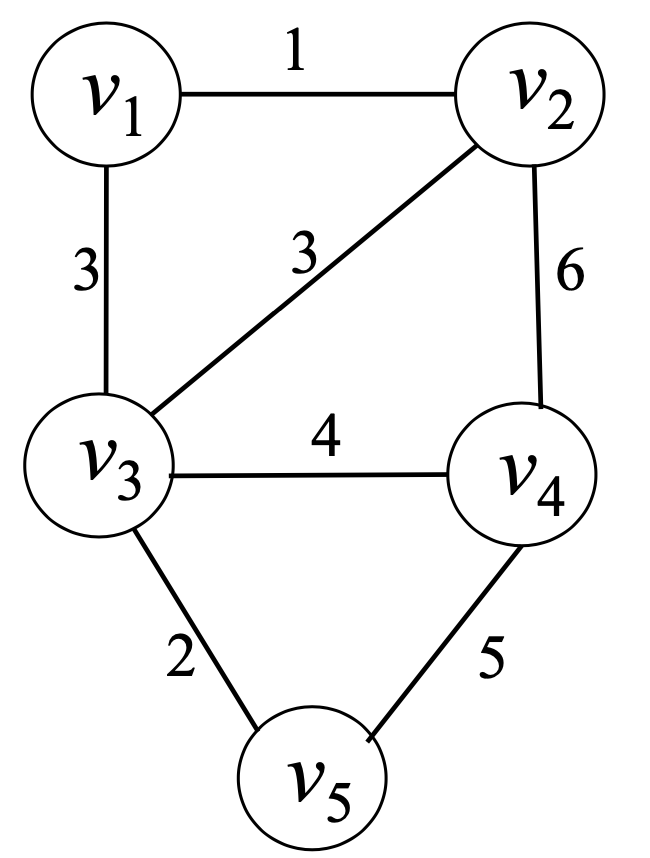
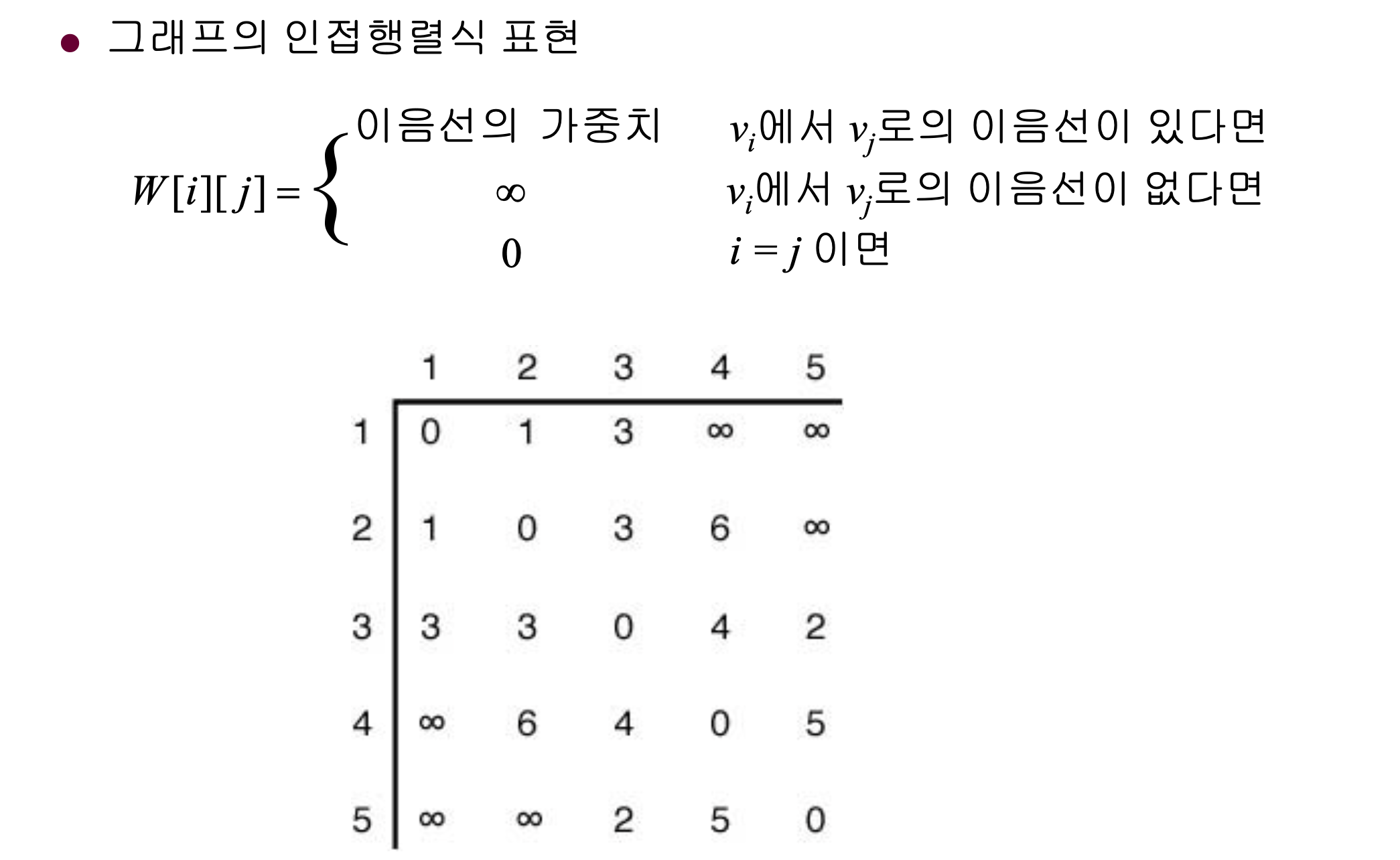
nearest[i] = Y에 속한 정점 중에서 vi에서 가장 가까운 정점의 인덱스
distance[i] = vi 와 nearest[i]를 잇는 이음선의 가중치
핵심적인 설계 구조
Y라는 노드들의 집합에 노드를 한 개씩 추가하며 Y와 Y가 아닌 노드들간의 거리 중 최적의 거리인 것을 골라 간선을 하나씩 추가하여 모든 노드가 Y에 들어가면 추가된 간선을 통해 MST가 완성된다.
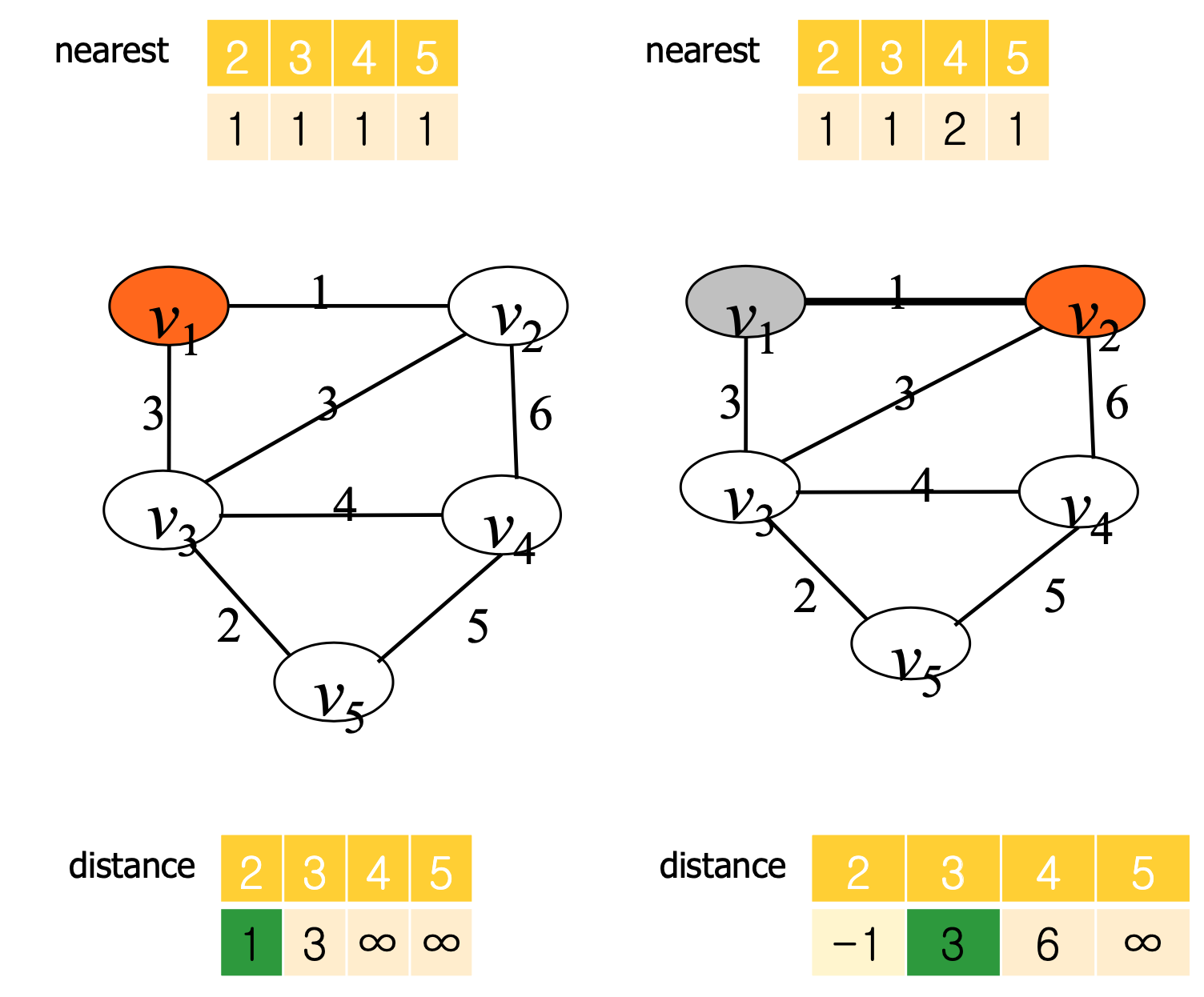
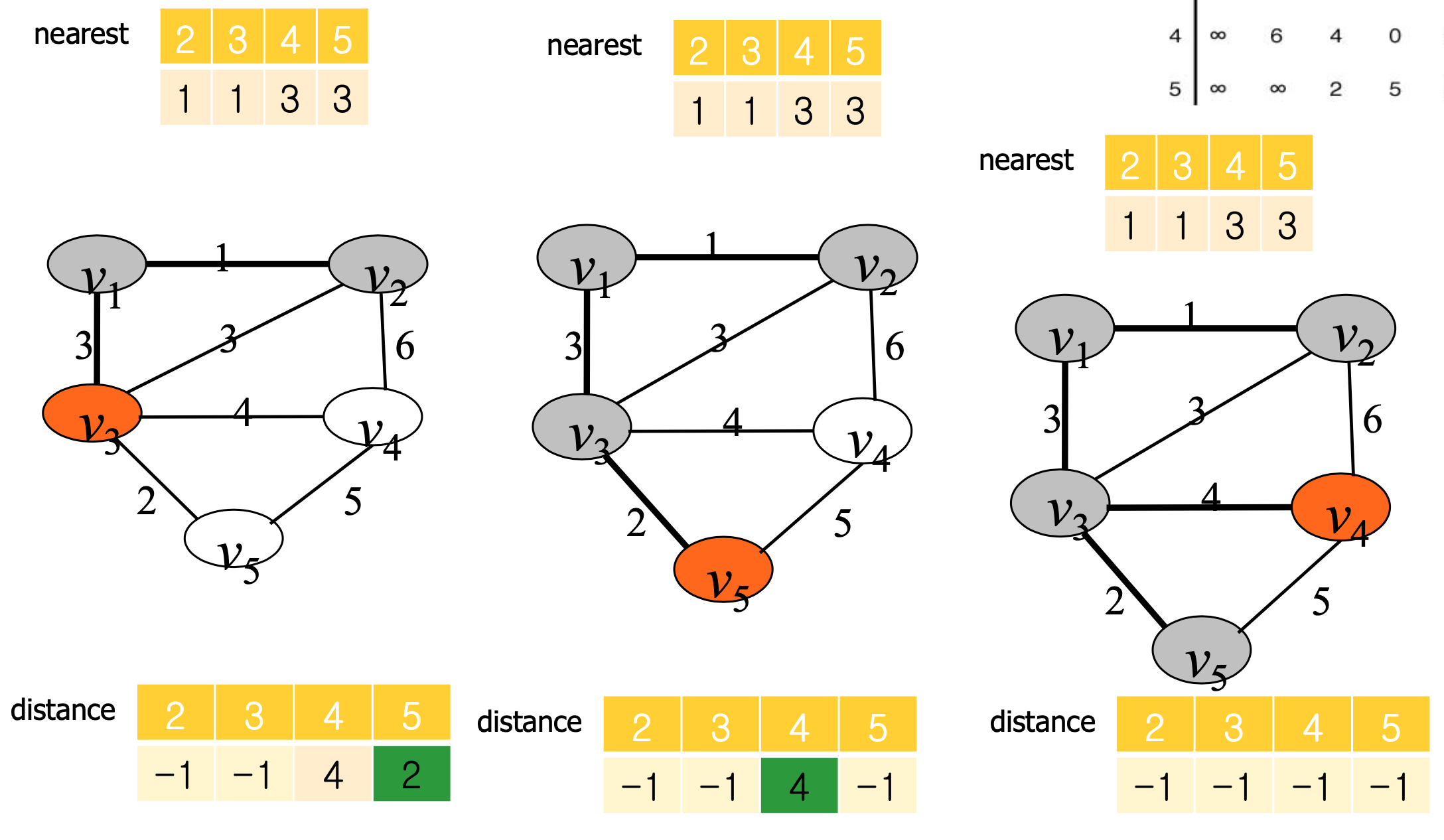
void prim(int n, const number W[][], set_of_edges& F) {
index i, vnear; number min; edge e;
index nearest[2..n]; number distance[2..n];
F = 공집합;
for(i=2; i <= n; i++) { // 초기화
nearest[i] = 1; // vi에서 가장 가까운 정점을 v1으로 초기화
distance[i] = W[1][i]; // vi과 v1을 잇는 이음선의 가중치로 초기화
}
repeat(n-1 times) { // n-1개의 정점을 Y에 추가한다{
min = “infinite”;
for(i=2; i <= n; i++) // 각 정점에 대해서
if (0 <= distance[i] <= min) { // distance[i]를 검사하여
min = distance[i]; // 가장 가까이 있는 vnear을
vnear = i; // 찾는다.
}
e = edge connecting vertices indexed by vnear and nearest[vnear];
add e to F;
distance[vnear] = -1; // 찾은 노드를 Y에 추가한다.
for(i=2; i <= n; i++)
if (W[i][vnear] < distance[i]) { // Y에 없는 각 노드에 대해서
distance[i] = W[i][vnear]; // distance[i]를 갱신한다.
nearest[i] = vnear;
}
}
}
시간 복잡도:
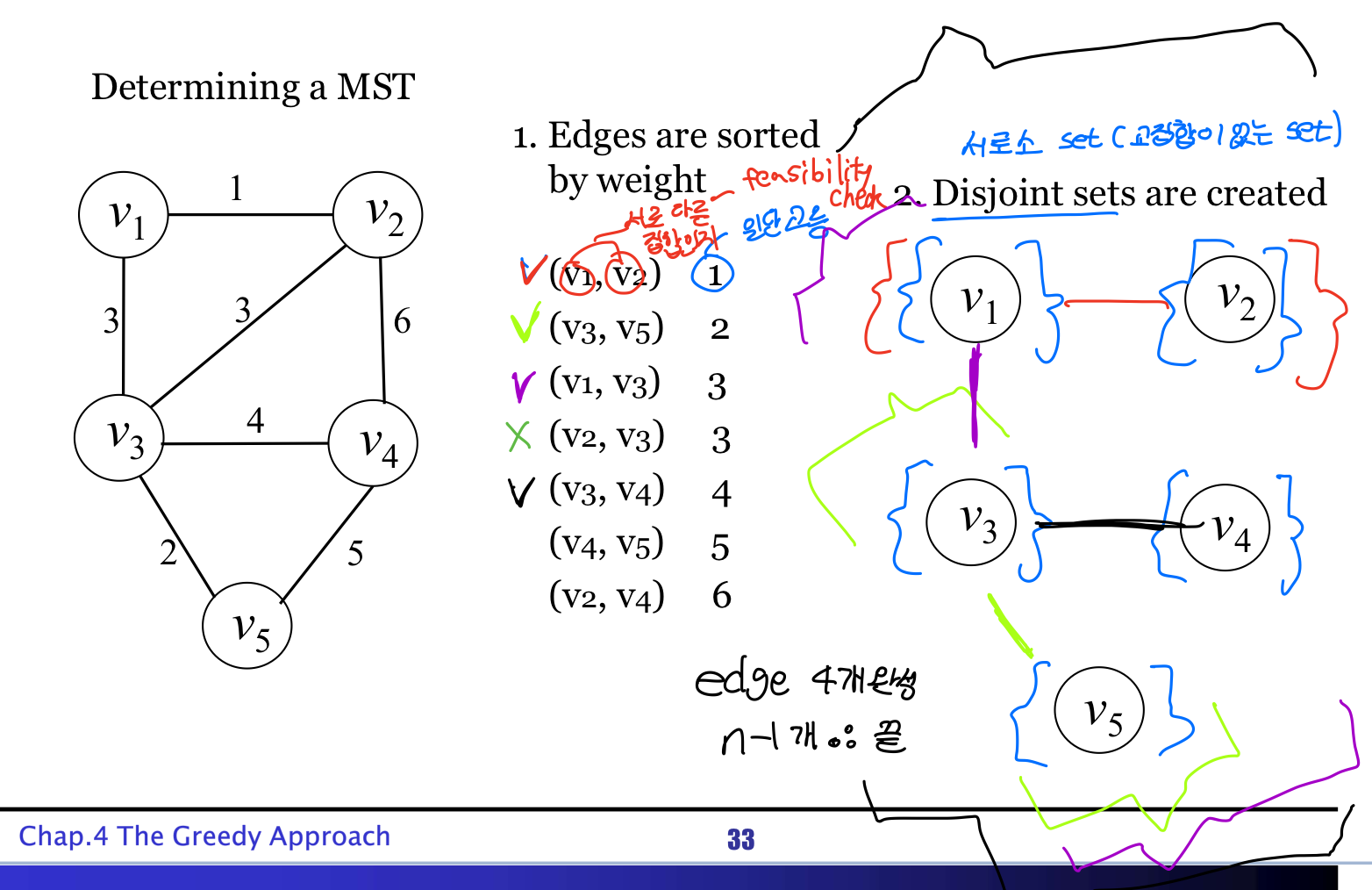
⭐Kruskal's Algorithm(MST)
핵심적인 설계 구조
노드 한 개당 집합 한개를 만들어 작은 간선부터 하나씩 골라 서로소인 집합이라면
집합을 합치고 아니면 PASS하여 MST를 완성한다.
void kruskal(int n, int m, set_of_edges E, set_of_edges& F) {
index i, j;
set_pointer p, q;
edge e;
Sort the m edges in E by weight in nondecreasing order;
F = 공집합;
initial(n);
while (number of edges in F is less than n-1) {
e = edges with least weight not yet considered;
i, j = indices of vertices connected by e;
p = find(i);
q = find(j);
if (!equal(p,q)) {
merge(p,q);
add e to F;
}
}
}⭐KrusKal에서 사용되는 자료구조 비교
Disjoint Set Data Structure 1
The worst-case of comparisons : order of
Disjoint Set Data Structure 2
The worst-case of comparisons : order of m lg m
이 둘의 차이점은 merge에 있다 Disjoint Set Data Structure 2는
단지 트리의 꼬리에 계속 붙여 일자로 만드는 것이 아닌 두 트리가 같은 레벨일때만 레벨이 +1 되도록 더 작은 level의 트리를 더 큰 level의 트리에 붙인다. 이 덕에 시간 복잡도가 크게 줄어든다.
최종 시간 복잡도=
⭐ 이렇게 알고리즘의 시간복잡도는 그 알고리즘을 구현하는데 사용하는 자료구조에 좌우되는 경우도 있다.
⭐ 알고리즘을 고치기는 쉬워도 자료구조는 고치기 힘들기에 초기에 자료구조를 잘 선택해야 한다.
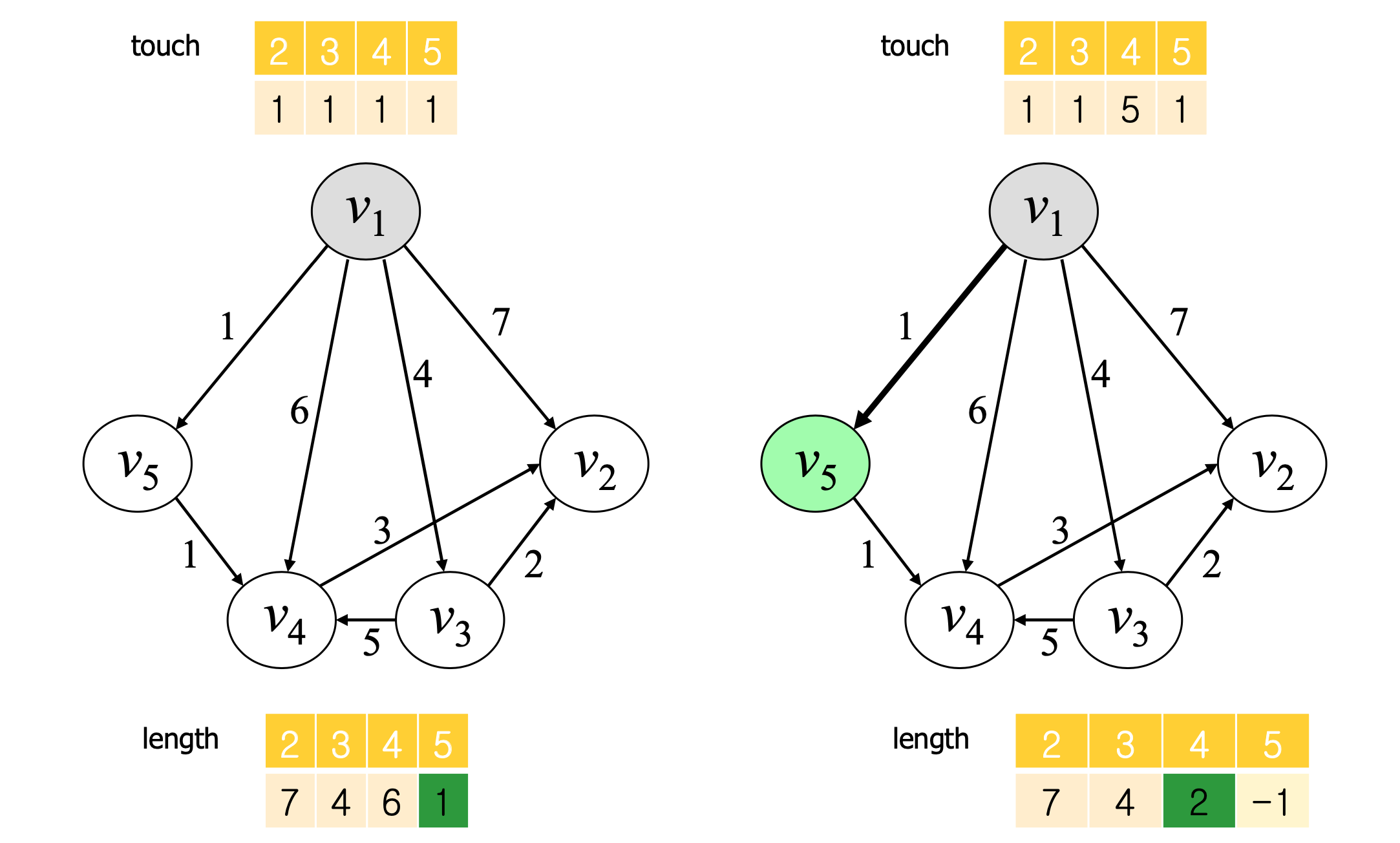
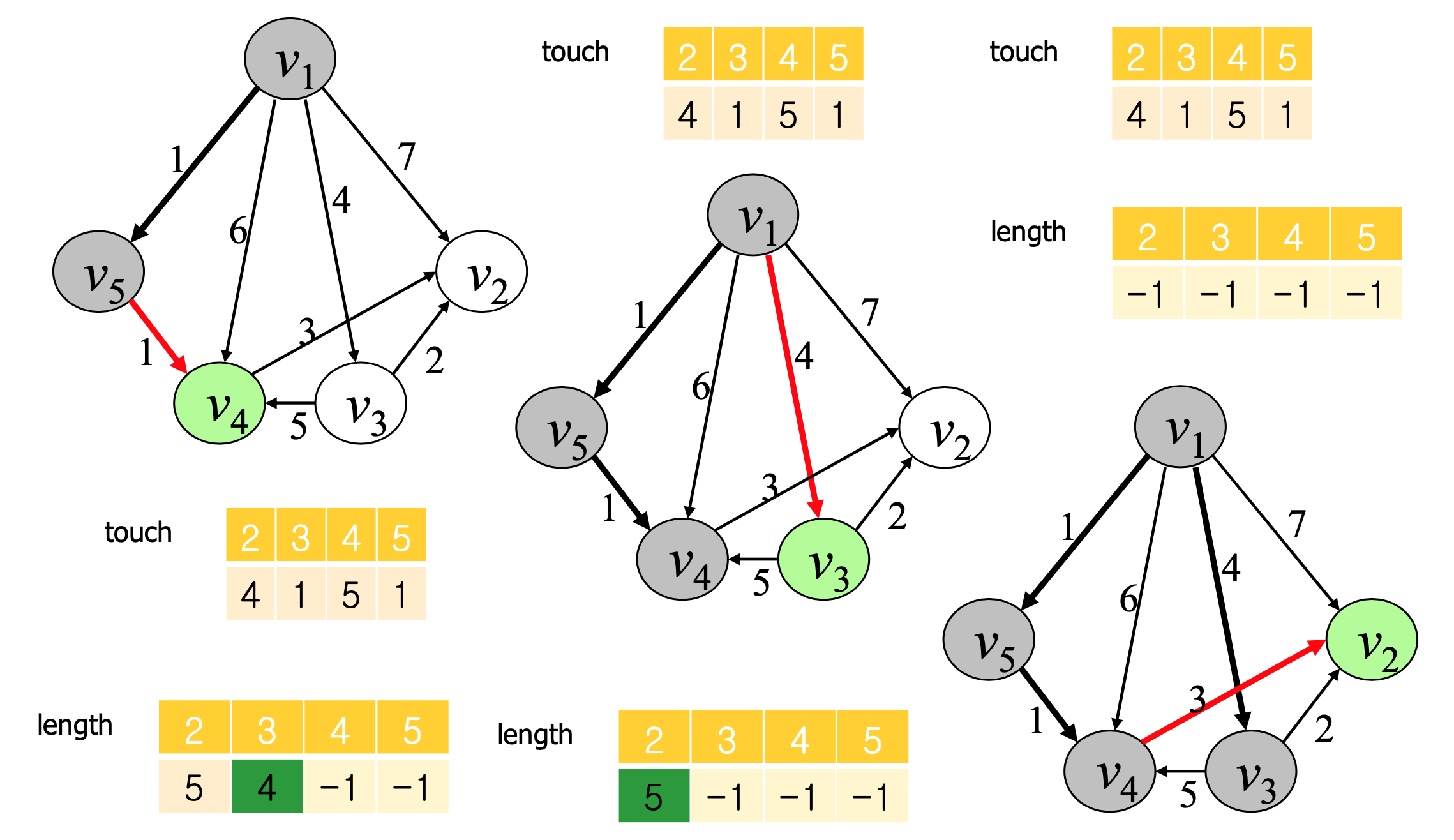
⭐Dijkstra's Algorithm
핵심적인 설계 구조
출발 노드에서 연결된 출발 노드와의 경로가 가장 작은 노드를 골라 그 노드를 거쳐갈 때 더 작은 경로인 경우 갱신해주고 그 노드는 다음에 고르지 않도록 한다. 이러한 과정을 반복하여 모든 노드가 한 번씩 선택된다면 출발지에서 최선의 경로가 구해진다.
touch[i] = 마지막으로 거쳐가는 노드
distance[i] = 노드와의 최적의 거리 (골라진 노드만 거쳐가는 경우일 때의)
void dijkstra (int n, const number W[][], set_of_edges& F) {
index i, vnear; edge e;
index touch[2..n]; number length[2..n];
F = 공집합;
for(i=2; i <= n; i++) { // For all vertices, initialize v1 to be the last
touch[i] = 1; // vertex on the current shortest path from v1,
length[i] = W[1][i]; // and initialize length of that path to be the
} // weight on the edge from v1.
repeat(n-1 times) { // Add all n-1 vertices to Y.
min = “infinite”;
for(i=2; i <= n; i++) // Check each vertex for having shortest path.
if (0 <= length[i] <= min) {
min = length[i];
vnear = i;
}
e = edge from vertex indexed by touch[vnear] to vertex indexed by vnear;
add e to F;
for(i=2; i <= n; i++)
if (length[vnear] + W[vnear][i] < length[i]) {
length[i] = length[vnear] + W[vnear][i];
touch[i] = vnear; // For each vertex not in Y, update its shortest
} // path. Add vertex indexed by vnear to Y. length[vnear] = -1;
}
}시간 복잡도:
⭐The knapsack Problem - 배낭문제
Knapsack Problem이란?
배낭 문제는 조합 최적화의 유명한 문제이다. 간단하게 말하면, 한 여행가가 가지고 가는 배낭에 담을 수 있는 무게의 최댓값이 정해져 있고, 일정 가치와 무게가 있는 짐들을 배낭에 넣을 때, 가치의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제이다.
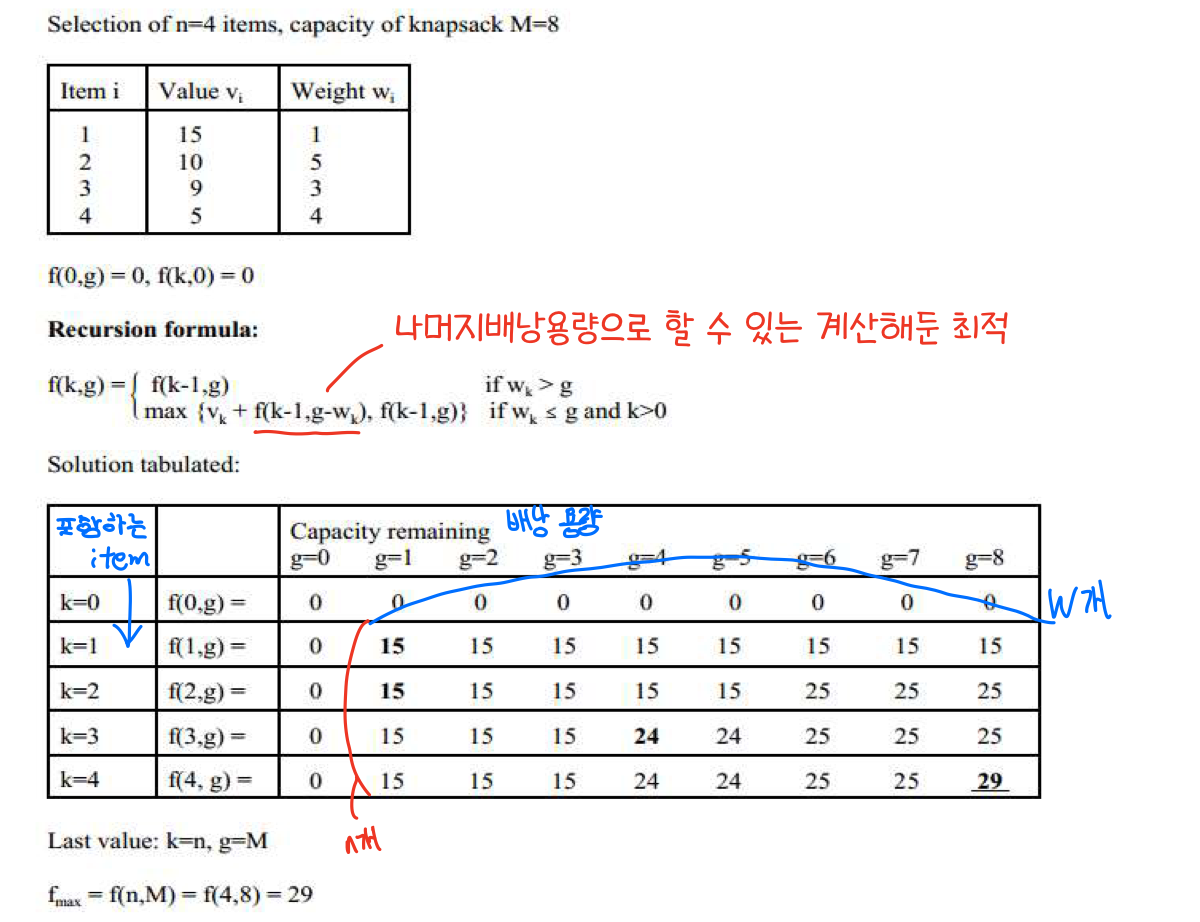

최악의 경우 시간 복잡도: - NP 문제
- NP문제
아직 아무도 이 문제의 최악의 경우 수행시간이 지수(exponential)보다 나은 알고리즘을 발견하지 못했고, 아직 아무도 그러한 알고리즘은 없다라고 증명한 사람도 없다.



